北师八上3.3轴对称与坐标变化

(共25张PPT)
第三章 位置与坐标
3.3轴对称与坐标变化
北师大版 数学 八年级 上册
学习目标
1．在同一直角坐标系中，感受图形上点的坐标变化与图形的轴对称变换之间的关系。
2．经历图形坐标变化与图形轴对称之间关系的探索过程，发展形象思维能力和数形结合意识。
3．经历探究物体与图形的形状、大小、位置关系和变换的过程，掌握空间与图形的基础知识和基本技能，培养学生的探索能力。
情景导入
如图，你能画出把鱼往左平移 6 格后所得的图形吗？
y
x
O
建立如图所示的平面直角坐标系，平移这个图形，图形上的点的坐标发生了什么变化呢？
探索新知
轴对称与坐标变化
一
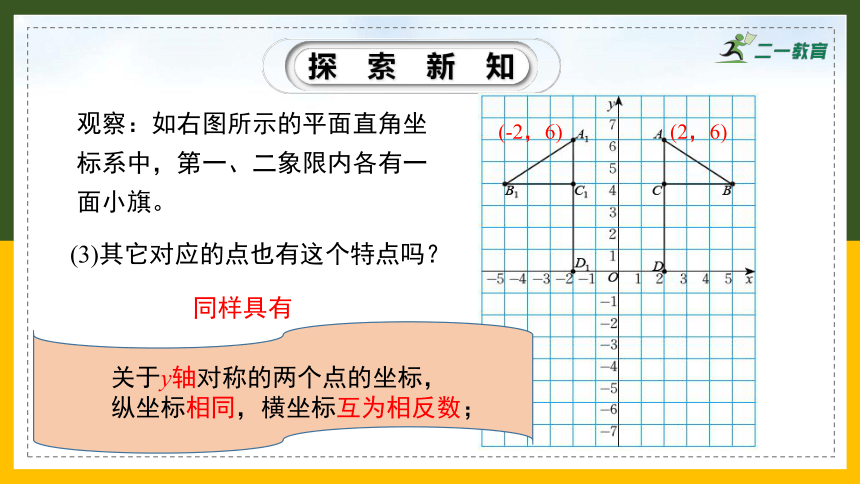
观察：如右图所示的平面直角坐标系中，第一、二象限内各有一面小旗。
(1)两面小旗之间有怎样的位置关系？
关于y轴成轴对称
(2，6)
(-2，6)
A B C D
A1 B1 C1 D1
探索新知
(2)对应点的坐标又有什么特点？
纵坐标相同，横坐标互为相反数
( 2 , 6)
( 5 , 4)
( -2,6)
( -5,4)
( 2 , 4)
( -2,4)
( 2, 0)
( -2,0)
观察：如右图所示的平面直角坐标系中，第一、二象限内各有一面小旗。
(2，6)
(-2，6)
探索新知
(3)其它对应的点也有这个特点吗？
同样具有
观察：如右图所示的平面直角坐标系中，第一、二象限内各有一面小旗。
(2，6)
(-2，6)
关于y轴对称的两个点的坐标，
纵坐标相同，横坐标互为相反数；
探索新知
想一想如果关于x轴对称呢？
(4)在这个坐标系里画出小旗ABCD关于x轴的对称图形，它的各个“顶点”的坐标与原来的点的坐标有什么关系？
横坐标相等，
纵坐标互为相反数.
(2，6)
(2，-6)
探索新知
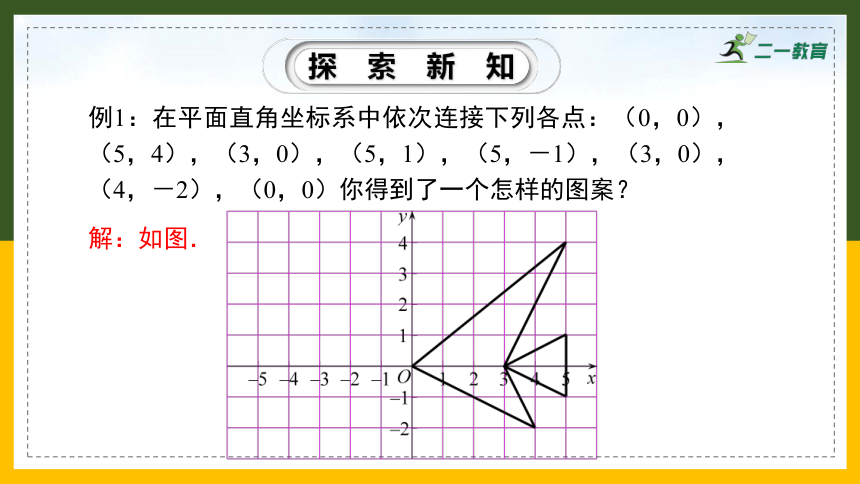
例1：在平面直角坐标系中依次连接下列各点：（0，0），（5，4），（3，0），（5，1），（5，－1），（3，0），（4，－2），（0，0）你得到了一个怎样的图案？
解：如图．
探索新知
　　做以下变化：
　　（1）纵坐标保持不变，横坐标分别乘以-1，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化？
　　分析：变化后的点的坐标依次为（0，0），（-5，4），（-3，0），（-5，1），（-5，-1），（-3，0）， （-4，-2），（0，0）．
探索新知
如图，所得的图案与原来的图案关于y轴对称．
探索新知
　　（2）横坐标保持不变，纵坐标分别乘以-1，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化？
　　分析：变化后的点的坐标依次为（0，0），（5，-4），（3，0），（5，-1），（5，1），（3，0），（4，2），（0，0）．
探索新知
如图，所得的图案与原来的图案关于x轴对称．
总结归纳
探索新知
(x , y)
(-x , y)
2.关于x轴对称的两个图形上点的坐标特征：
3.关于原点轴对称的两个图形上点的坐标特征：
(x , y)
( x , -y)
(x , y)
(-x , -y)
横坐标变为相反数，纵坐标不变.
横坐标不变，纵坐标变为相反数.
横坐标、纵坐标都变为相反数.
1.关于y轴对称的两个图形上点的坐标特征：
当堂检测
1. 在平面直角坐标系中，点 A （3，2）关于原点对称的
点的坐标是（　D　）
A. （－3，2） B. （3，－2）
C. （－2，－3） D. （－3，－2）
D
当堂检测
2. 将第一象限的“小旗”各点的横坐标分别乘－1，纵
坐标保持不变，符合上述要求的图形是（　C　）
A
B
C
D
C
当堂检测
3.如图，蝴蝶剪纸是一幅轴对称图形，将其放在平面直角坐标系中，如果图中点 E 的坐标为(m，1)，其关于 y 轴对称的点 F 的坐标(2，n)，则(m+n) 2 025 的值为( )
A．1 B．－1
C．32 025 D．0
B
当堂检测
4. 如图，在直角坐标系中，长方形 ABCO 的边 OA 在 x 轴
上，边 OC 在 y 轴上，点 B 的坐标为（1，3）.将长方形
沿对角线 AC 翻折，点 B 落在点 D 的位置，且 AD 交 y 轴
于点 E . 那么点 E 的坐标是 .
　
当堂检测
5. （1）若 ＋（ b －3）2＝0，则点 A （ a ， b ）关
于 x 轴对称的点的坐标为 ；
（2）点 P （－2，1）与点 Q （ a ， b ）关于 y 轴对称，
则 a ＋ b ＝ .
（4，－3）　
3　
当堂检测
6.如图，在平面直角坐标系中，每个小正方形的边长均为 1.
(1)点 A 在第____ 象限，
它的坐标是_________ ；
(2)点 B 在第___象限，它的坐标是_________ ；
(3)将△ AOB 每个顶 点的 横 坐 标 保 持 不变，
纵坐标都乘－1，再顺次连接这些点，所得的
图 形 与△ AOB 关于______轴对称．
四
(3，－2)　
二
(－2，4)
x
当堂检测
（1） S△ ABC ＝ ；
　
7. 如图，在平面直角坐标系内，△ ABC 的三个顶点的坐
标分别为 A （0，3）， B （3，4）， C （2，2）.
当堂检测
（2）画出△ ABC 关于 x 轴的对称图形△ A1 B1 C1，再画
出△ A1 B1 C1关于 y 轴的对称图形△ A2 B2 C2.
解：（2）如图，△ A1 B1 C1和△ A2 B2 C2即为所求.
当堂检测
8.已知点A(2a＋b，5＋a)，B(2b－1，－a＋b).
(1)若点A，B关于x轴对称，求a，b的值；
(2)若点A，B关于y轴对称，求(4a＋4b)2 025 的值.
解：（1）因为点A，B关于x轴对称，
所以2a＋b＝2b－1，5＋a－a＋b＝0，
解得a＝－3，b＝－5.
当堂检测
8.已知点A(2a＋b，5＋a)，B(2b－1，－a＋b).
(1)若点A，B关于x轴对称，求a，b的值；
(2)若点A，B关于y轴对称，求(4a＋4b)2 025 的值.
解：（2）因为点A，B关于y轴对称，
所以2a＋b＋2b－1＝0，5＋a＝－a＋b，
解得 a＝－，b＝.
所以(4a＋4b)2 025＝(－7＋6)2 025＝(－1)2 025＝－1.
关于轴对称的两个点的坐标特征
1.关于x轴对称的两个点的坐标：
横坐标保持相同，纵坐标互为相反数
2.关于y轴对称的两个点的坐标：
纵坐标保持相同，横坐标互为相反数。
3.关于原点对称的两个点的坐标：
横、纵坐标都互为相反数。
感谢收看