人教版数学八年级下册 第十七章勾股定理 基础复习(含答案)
文档属性
| 名称 | 人教版数学八年级下册 第十七章勾股定理 基础复习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 953.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 00:00:00 | ||
图片预览


文档简介
第十七章基础复习
知识点 1 勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么
1. 勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是 ( )
2. 如图在正方形网格中,每个小正方形的边长均为1,则在△ABC中,边长为无理数的边有 ( )
A. 3条 B. 2 条 C. 1 条 D. 0 条
3. 一块圆形宣传标志牌如图所示,点 A,B,C在⊙O上,CD 垂直平分AB 于点 D.现测得AB =8 dm,DC=2 dm,则圆形标志牌的半径为 ( )
A. 6 dm B. 5 dm C. 4 dm D. 3 dm
4. 正方形ABCD 的边长为1,其面积记为S ,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为S ,…按此规律继续下去,则S 的值为 ( )
5. 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点 B,AB=4.则直线AB与ON之间的距离是 ( )
A. B. 2 D. 4
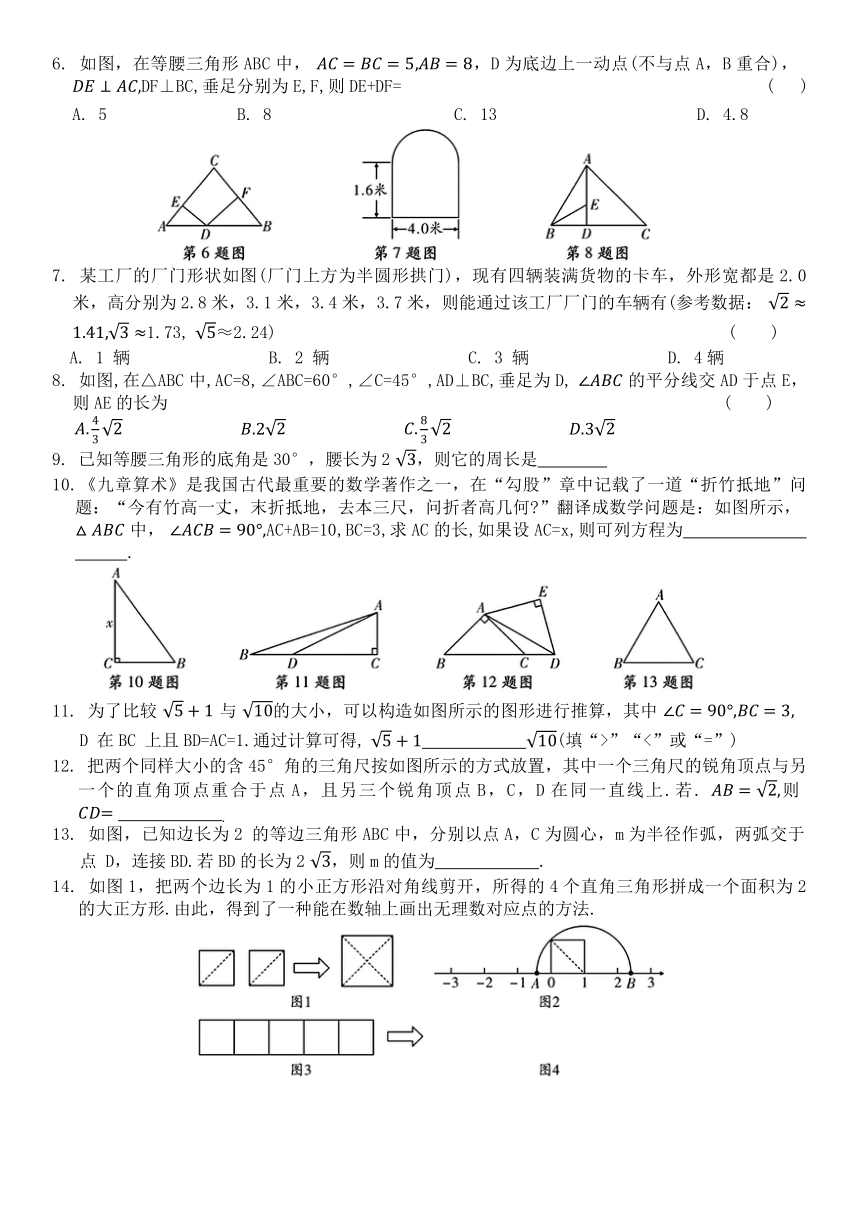
6. 如图,在等腰三角形ABC中, ,D为底边上一动点(不与点A,B重合), DF⊥BC,垂足分别为E,F,则DE+DF= ( )
A. 5 B. 8 C. 13 D. 4.8
7. 某工厂的厂门形状如图(厂门上方为半圆形拱门),现有四辆装满货物的卡车,外形宽都是2.0米,高分别为2.8米,3.1米,3.4米,3.7米,则能通过该工厂厂门的车辆有(参考数据: 1.73, ≈2.24) ( )
A. 1 辆 B. 2 辆 C. 3 辆 D. 4辆
8. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D, 的平分线交AD于点E,则AE的长为 ( )
9. 已知等腰三角形的底角是30°,腰长为2 ,则它的周长是
10.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何 ”翻译成数学问题是:如图所示, 中, AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为 .
11. 为了比较 与 的大小,可以构造如图所示的图形进行推算,其中 D 在BC 上且BD=AC=1.通过计算可得, (填“>”“<”或“=”)
12. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若. 则
13. 如图,已知边长为2 的等边三角形ABC中,分别以点A,C为圆心,m为半径作弧,两弧交于点 D,连接BD.若BD的长为2 ,则m的值为 .
14. 如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
(1)图2中A,B两点表示的数分别为 , .
(2)请你参照上面的方法,把长为5,宽为1的长方形进行裁剪,拼成一个正方形.
①在图3 中画出裁剪线,并在图4位置画出所拼正方形的示意图.
②在数轴上分别标出表示数 以及、 的点.(图中标出必要线段长)
15. 如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西 方向航行10km至C 港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:
(2)确定C港在A 港的什么方向.
16. 如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中, 90°,BC=a,AC=b,AB=c,正方形IECF中,
小明发明了求正方形边长的方法:由题意可得 因为 AD,所以a-x+b-x=c,解得
小亮也发现了另一种求正方形边长的方法:利用 可以得到x与a,b,c的关系.
(1)请根据小亮的思路完成他的求解过程.
(2)请结合小明和小亮得到的结论验证勾股定理.
知识点 2 勾股定理的逆定理
1. 如果两个命题的题设和结论正好相反,那么这样的两个命题叫做互逆命题,如果把其中一个叫做原命题,那么另一个叫做它的逆命题.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理为互逆定理,其中一个定理称为另一个定理的逆定理.
2. 勾股定理的逆定理:如果三角形的三边长a,b,c满足 那么这个三角形是直角三角形.
3. 勾股数:能够成为直角三角形三条边长的三个正整数,称为勾股数.
17. 下列各组数是勾股数的是 ( )
A. 4,5,6 B. 1, , C. 9,40,41 D. 3.6,4.8,6
18. 下列条件中,不能说明△ABC是直角三角形的是 ( )
C.∠C=∠A-∠B D.∠A:∠B:∠C=3:4:5
19. 已知M,N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是 ( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
20. 如图,四边形ABCD中, ,则∠ADC的度数为
( )
A. 120° B. 105° C. 135° D. 125°
21. 已知下列命题:①若a>b,则 ac> bc;②若a=1,则 ③角平分线上的点到角两边的距离相等.其中原命题与逆命题均为真命题的是 .
22. 如图所示的网格是正方形网格,则∠PAB+∠PBA= (点A,B,P是网格线交点).
23. 某住宅小区有一块草坪如图所示,已知, 且 则这块草坪的面积是 m .
24. 能够成为直角三角形三边长的三个正整数,我们称之为一组勾股数,观察下列表格:
3,4,5 3 +4 =5
5,12,13 5 +12 =13
7,24,25 7 +24 =25
9,40,41 9 +40 =41
… …
a,b,c a +b =c
(1)试找出它们的共同点,由它们的共同点得出并证明一个结论.
(2)写出当a=17时,b,c的值.
第十七章基础复习
1. B 2. B 3. B 4. A 5. C 6. D 7. B 8. C
11. > 12. -1 13. 2 或
14. 解:(1)由图可得,点A 到原点的距离为: 点 A在原点左侧,∴点A 表示的数为 由图可得,点B到原点的距离为: 点 B在原点右侧,∴点 B表示的数为 故答案为:
(2)①如图所示:
②表示数 以及 的点如图所示:
15. 解:(1)由题意,可得 在 中,
即A,C两地之间的距离为14.1 km.
(2)由(1)知, 为等腰直角三角形,
∴C港在A港北偏东1 的方向上.
16. 解:(1
(2)由题意,得 即 c),化简得
17. C 18. D 19. B 20. C
21.③ 22. 45° 23. 144
24. 解:(1)共同点:①各组数均满足 ②最小的数是奇数,其余的两个数是连续的正整数;③最小的数的平方等于另两个连续整数的和,如 ·由以上共同点我们可得出这样一个结论:设m为大于1的奇数,将 拆分为两个连续的整数之和,即 1),则m,n, l 就构成一组简单的勾股数.
证明: (m为大于1的奇数),.
∴m,n,n+l 是一组勾股数.
(2)由(1)中的结论可知, 当 时, 解得 则
知识点 1 勾股定理
如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么
1. 勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是 ( )
2. 如图在正方形网格中,每个小正方形的边长均为1,则在△ABC中,边长为无理数的边有 ( )
A. 3条 B. 2 条 C. 1 条 D. 0 条
3. 一块圆形宣传标志牌如图所示,点 A,B,C在⊙O上,CD 垂直平分AB 于点 D.现测得AB =8 dm,DC=2 dm,则圆形标志牌的半径为 ( )
A. 6 dm B. 5 dm C. 4 dm D. 3 dm
4. 正方形ABCD 的边长为1,其面积记为S ,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积为S ,…按此规律继续下去,则S 的值为 ( )
5. 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点 B,AB=4.则直线AB与ON之间的距离是 ( )
A. B. 2 D. 4
6. 如图,在等腰三角形ABC中, ,D为底边上一动点(不与点A,B重合), DF⊥BC,垂足分别为E,F,则DE+DF= ( )
A. 5 B. 8 C. 13 D. 4.8
7. 某工厂的厂门形状如图(厂门上方为半圆形拱门),现有四辆装满货物的卡车,外形宽都是2.0米,高分别为2.8米,3.1米,3.4米,3.7米,则能通过该工厂厂门的车辆有(参考数据: 1.73, ≈2.24) ( )
A. 1 辆 B. 2 辆 C. 3 辆 D. 4辆
8. 如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D, 的平分线交AD于点E,则AE的长为 ( )
9. 已知等腰三角形的底角是30°,腰长为2 ,则它的周长是
10.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何 ”翻译成数学问题是:如图所示, 中, AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为 .
11. 为了比较 与 的大小,可以构造如图所示的图形进行推算,其中 D 在BC 上且BD=AC=1.通过计算可得, (填“>”“<”或“=”)
12. 把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另三个锐角顶点B,C,D在同一直线上.若. 则
13. 如图,已知边长为2 的等边三角形ABC中,分别以点A,C为圆心,m为半径作弧,两弧交于点 D,连接BD.若BD的长为2 ,则m的值为 .
14. 如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法.
(1)图2中A,B两点表示的数分别为 , .
(2)请你参照上面的方法,把长为5,宽为1的长方形进行裁剪,拼成一个正方形.
①在图3 中画出裁剪线,并在图4位置画出所拼正方形的示意图.
②在数轴上分别标出表示数 以及、 的点.(图中标出必要线段长)
15. 如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西 方向航行10km至C 港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:
(2)确定C港在A 港的什么方向.
16. 如图,将直角三角形分割成一个正方形和两对全等的直角三角形,直角三角形ABC中, 90°,BC=a,AC=b,AB=c,正方形IECF中,
小明发明了求正方形边长的方法:由题意可得 因为 AD,所以a-x+b-x=c,解得
小亮也发现了另一种求正方形边长的方法:利用 可以得到x与a,b,c的关系.
(1)请根据小亮的思路完成他的求解过程.
(2)请结合小明和小亮得到的结论验证勾股定理.
知识点 2 勾股定理的逆定理
1. 如果两个命题的题设和结论正好相反,那么这样的两个命题叫做互逆命题,如果把其中一个叫做原命题,那么另一个叫做它的逆命题.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理为互逆定理,其中一个定理称为另一个定理的逆定理.
2. 勾股定理的逆定理:如果三角形的三边长a,b,c满足 那么这个三角形是直角三角形.
3. 勾股数:能够成为直角三角形三条边长的三个正整数,称为勾股数.
17. 下列各组数是勾股数的是 ( )
A. 4,5,6 B. 1, , C. 9,40,41 D. 3.6,4.8,6
18. 下列条件中,不能说明△ABC是直角三角形的是 ( )
C.∠C=∠A-∠B D.∠A:∠B:∠C=3:4:5
19. 已知M,N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是 ( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
20. 如图,四边形ABCD中, ,则∠ADC的度数为
( )
A. 120° B. 105° C. 135° D. 125°
21. 已知下列命题:①若a>b,则 ac> bc;②若a=1,则 ③角平分线上的点到角两边的距离相等.其中原命题与逆命题均为真命题的是 .
22. 如图所示的网格是正方形网格,则∠PAB+∠PBA= (点A,B,P是网格线交点).
23. 某住宅小区有一块草坪如图所示,已知, 且 则这块草坪的面积是 m .
24. 能够成为直角三角形三边长的三个正整数,我们称之为一组勾股数,观察下列表格:
3,4,5 3 +4 =5
5,12,13 5 +12 =13
7,24,25 7 +24 =25
9,40,41 9 +40 =41
… …
a,b,c a +b =c
(1)试找出它们的共同点,由它们的共同点得出并证明一个结论.
(2)写出当a=17时,b,c的值.
第十七章基础复习
1. B 2. B 3. B 4. A 5. C 6. D 7. B 8. C
11. > 12. -1 13. 2 或
14. 解:(1)由图可得,点A 到原点的距离为: 点 A在原点左侧,∴点A 表示的数为 由图可得,点B到原点的距离为: 点 B在原点右侧,∴点 B表示的数为 故答案为:
(2)①如图所示:
②表示数 以及 的点如图所示:
15. 解:(1)由题意,可得 在 中,
即A,C两地之间的距离为14.1 km.
(2)由(1)知, 为等腰直角三角形,
∴C港在A港北偏东1 的方向上.
16. 解:(1
(2)由题意,得 即 c),化简得
17. C 18. D 19. B 20. C
21.③ 22. 45° 23. 144
24. 解:(1)共同点:①各组数均满足 ②最小的数是奇数,其余的两个数是连续的正整数;③最小的数的平方等于另两个连续整数的和,如 ·由以上共同点我们可得出这样一个结论:设m为大于1的奇数,将 拆分为两个连续的整数之和,即 1),则m,n, l 就构成一组简单的勾股数.
证明: (m为大于1的奇数),.
∴m,n,n+l 是一组勾股数.
(2)由(1)中的结论可知, 当 时, 解得 则
