人教版数学八年级下册 第十七章 勾股定理 综合测试卷(含答案)
文档属性
| 名称 | 人教版数学八年级下册 第十七章 勾股定理 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 22:07:09 | ||
图片预览


文档简介
第十七章综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
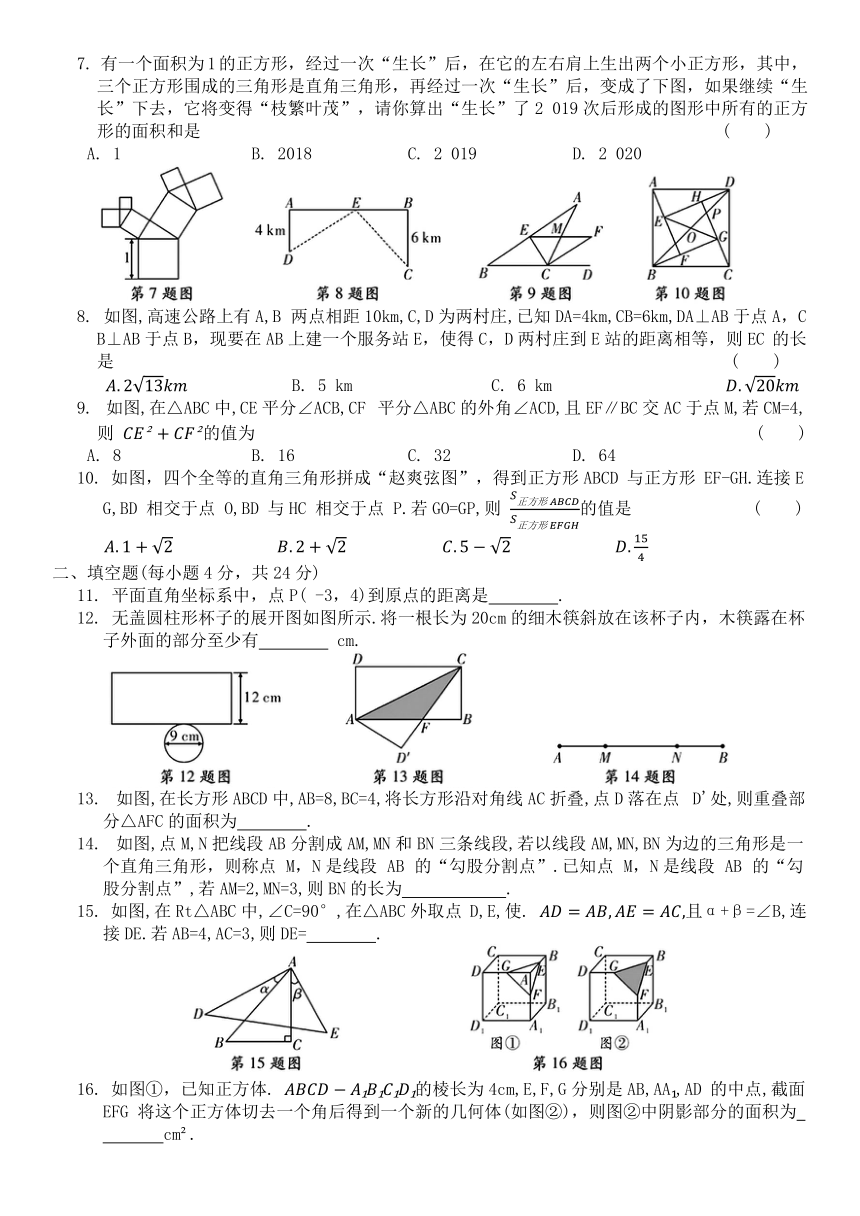
1. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD 的面积为 ( )
A. B. 3 C. D. 5
2. 如图,数轴上点A,B分别对应实数1,2,过点 B 作PQ⊥AB,以点 B 为圆心,AB长为半径画弧,交 PQ于点C,以点A 为圆心,AC长为半径画弧,交数轴于点 M,则点 M对应的实数的平方是 ( )
A. 2 B. 5
3. 一个三角形的三边长分别为 ab,则这个三角形的形状为 ( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 形状不能确定
4. 如图,已知S ,S 和S 分别是以Rt△ABC的斜边AB及直角边BC和AC为直径的半圆的面积,则S ,S 和S 满足的关系式为 ( )
5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为 ( )
A. 9 B. 6 C. 4 D. 3
6. 如图,将两个大小、形状完全相同的△ABC和△A'B'C'拼在一起,其中点A'与点A重合,点 C'落在边AB 上,连接B'C.若 ,则 B'C 的长为( )
B. 6
7. 有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2 019次后形成的图形中所有的正方形的面积和是 ( )
A. 1 B. 2018 C. 2 019 D. 2 020
8. 如图,高速公路上有A,B 两点相距10km,C,D为两村庄,已知DA=4km,CB=6km,DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离相等,则EC 的长是 ( )
B. 5 km C. 6 km
9. 如图,在△ABC中,CE平分∠ACB,CF 平分△ABC的外角∠ACD,且EF∥BC交AC于点M,若CM=4,则 的值为 ( )
A. 8 B. 16 C. 32 D. 64
10. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形 EF-GH.连接EG,BD 相交于点 O,BD 与HC 相交于点 P.若GO=GP,则 的值是 ( )
二、填空题(每小题4分,共24分)
11. 平面直角坐标系中,点P( -3,4)到原点的距离是 .
12. 无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.
13. 如图,在长方形ABCD中,AB=8,BC=4,将长方形沿对角线AC折叠,点D落在点 D'处,则重叠部分△AFC的面积为 .
14. 如图,点M,N把线段AB分割成AM,MN和BN三条线段,若以线段AM,MN,BN为边的三角形是一个直角三角形,则称点 M,N是线段 AB 的“勾股分割点”.已知点 M,N是线段 AB 的“勾股分割点”,若AM=2,MN=3,则BN的长为 .
15. 如图,在Rt△ABC中,∠C=90°,在△ABC外取点 D,E,使. 且α+β=∠B,连接DE.若AB=4,AC=3,则DE= .
16. 如图①,已知正方体. 的棱长为4cm,E,F,G分别是AB,AA ,AD 的中点,截面EFG将这个正方体切去一个角后得到一个新的几何体(如图②),则图②中阴影部分的面积为 cm .
三、解答题(共56分)
17. (8分)阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
18. (8分)如图,在四边形ABCD 中,∠DAB=30°,点E为AB的中点, 交AB于点E, ,BC=2,CD=4.
(1)求∠ABC的度数.
(2)求 CE的长.
19. (8分)如图,公路MN 和公路PQ 在点 P 处交汇,且. ,点A 处有一所中学, 160 m.若拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿 PN方向行驶时,
(1)学校是否会受到噪声影响 请说明理由.
(2)如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒
20. (10分)问题背景:在 中,AB,BC,AC三边的长分别为 求此三角形的面积.小辉同学在解答这道题时.先建立一个正方形网格(每个小正方形的边长为1).再在网格中画出格点. (即 三个顶点都在小正方形的顶点处),如图①所示.这样不需求 的高,而借用网格就能计算出它的面积.
(1)请你求出 的面积.
思维拓展:
(2)我们把上述求. 面积的方法叫做构图法.
如果 三边的长分别为 请利用图②的正方形网格(每个小正方形的边长为a)画出相应的. ,并求出它的面积.
探索创新:
(3)若 三边的长分别为 且 试运用构图法画出示意图并求出这三角形的面积.
21. (10分)通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边平方的2 倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗 (填“是”或“不是”).
(2)若某三角形的三边长分别为1, ,2,则该三角形是不是奇异三角形,请做出判断并写出判断依据.
(3)在 中,两边长分别为a,c,且 则这个三角形是不是奇异三角形 请做出判断并写出判断依据.
探究:在 Rt△ABC中, 且 若 是奇异三角形,求
22. (12 分)如图, 中, ,若点 P 从点 A 出发,以每秒1 个单位长度的速度沿折线 运动,设运动时间为t秒
(1)若点 P在AC上,且满足 时,求此时t的值.
(2)若点 P恰好在. 的平分线上,求t的值.
第十七章综合测试卷
1. B 2. C 3. B 4. B 5. D 6. A 7. D 8. A 9. D 10. B11. 5 12. 5 13. 10
14. 或 15. 5 16. 2
17. 解:当n=1时, ∵直角三角形有一边长为5,∴Ⅰ.当a=5时, 解得m (舍去);Ⅱ.当b=5时,即m=5,代入①③,得a=l2,c=13;Ⅲ. 当c=5时, 解得m=±3,∵m>0,∴m=3,代入①②,得a=4,b=3.综上所述,当n=1时,有一边长为5的直角三角形的另外两条边长分别为12,13或3,4.
18. 解:(1)如图,连接BD,∵ 点E为AB 的中点,DE⊥AB,∴BD=AD,AE=BE,
∵ ∠DAB = 30°,∴ ∠DBE = ∠DAB =
D 是直角三角形,且∠CBD=90°,
∴∠ABC=∠DBA+∠CBD=30°+90°=120°.
(2)如图,过点 C作CF⊥AB于点 F,则∠BFC=90°.
∵∠ABC=120°,∴∠BCF=30°,
∵ 在 Rt△BED 中,
19. 解:(1)如图,过点 A 作 AH⊥MN于点H,则∠AHP=90°,
在 Rt△APH中,∵∠HPA=30°,
∵80<100,
∴拖拉机在公路MN上沿PN方向行驶时学校会受到噪声影响.
(2)如图,假设拖拉机行驶到B点时开始影响学校,行驶到C点时结束对学校的影响,则AB=AC=100,∵AH⊥BC,∴BH=CH,在 Rt△ABH中,∠AHB=90°,AB=100,AH=80,
∴BC=2BH=120,
∵拖拉机的速度为18 km/h=5 m/s,
∴学校受到的影响的时间为: (秒).
20. 解:(1)△ABC的面积为:
(2)如图②,在边长为a的正方形网格中,△ABC即为所求作三角形,△ABC的面积为:
(3)如图③,在长为m、宽为n的网格中, 即为所求作三角形, 的面积为:
21. 解:(1)设等边三角形的边长为a,
∴等边三角形一定是奇异三角形.故答案为:是.
∴该三角形是奇异三角形.
(3)当c为斜边时, 不是奇异三角形;当b为斜边时,
是奇异三角形.
探究: 中,
是奇异三角形,
22. 解:(1)如图1,PA =PB,在 Rt△ACB 中,∠ACB = 由题得AP=t,则PB=t,PC=8-t,在 Rt△PCB中,由勾股定理得 解得 即当点P在AC上,且PA=PB时,t的值为
(2)分两种情况:①点P在BC上时,如图2所示,过点P作PE⊥AB于点E,则∠AEP=90°,
∵AP平分∠BAC,且PC⊥AC,
∴∠CAP=∠EAP,PE=PC,
在△ACP和△AEP中,
∴△ACP≌△AEP(AAS),∴AE=AC=8,∴BE=2,由题得PC=t-AC=t-8,则PE=t-8,PB=BC-PC=14-t,在 Rt△PEB 中,由勾股定理得 即 解得
②点P又回到A点时,∵AC+BC+AB=8+6+10=24,∴t=24.综上所述,点P在∠BAC的平分线上时,t的值为 或24.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD 的面积为 ( )
A. B. 3 C. D. 5
2. 如图,数轴上点A,B分别对应实数1,2,过点 B 作PQ⊥AB,以点 B 为圆心,AB长为半径画弧,交 PQ于点C,以点A 为圆心,AC长为半径画弧,交数轴于点 M,则点 M对应的实数的平方是 ( )
A. 2 B. 5
3. 一个三角形的三边长分别为 ab,则这个三角形的形状为 ( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 形状不能确定
4. 如图,已知S ,S 和S 分别是以Rt△ABC的斜边AB及直角边BC和AC为直径的半圆的面积,则S ,S 和S 满足的关系式为 ( )
5.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲. 如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为 ( )
A. 9 B. 6 C. 4 D. 3
6. 如图,将两个大小、形状完全相同的△ABC和△A'B'C'拼在一起,其中点A'与点A重合,点 C'落在边AB 上,连接B'C.若 ,则 B'C 的长为( )
B. 6
7. 有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了下图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2 019次后形成的图形中所有的正方形的面积和是 ( )
A. 1 B. 2018 C. 2 019 D. 2 020
8. 如图,高速公路上有A,B 两点相距10km,C,D为两村庄,已知DA=4km,CB=6km,DA⊥AB于点A,CB⊥AB于点B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离相等,则EC 的长是 ( )
B. 5 km C. 6 km
9. 如图,在△ABC中,CE平分∠ACB,CF 平分△ABC的外角∠ACD,且EF∥BC交AC于点M,若CM=4,则 的值为 ( )
A. 8 B. 16 C. 32 D. 64
10. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD 与正方形 EF-GH.连接EG,BD 相交于点 O,BD 与HC 相交于点 P.若GO=GP,则 的值是 ( )
二、填空题(每小题4分,共24分)
11. 平面直角坐标系中,点P( -3,4)到原点的距离是 .
12. 无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.
13. 如图,在长方形ABCD中,AB=8,BC=4,将长方形沿对角线AC折叠,点D落在点 D'处,则重叠部分△AFC的面积为 .
14. 如图,点M,N把线段AB分割成AM,MN和BN三条线段,若以线段AM,MN,BN为边的三角形是一个直角三角形,则称点 M,N是线段 AB 的“勾股分割点”.已知点 M,N是线段 AB 的“勾股分割点”,若AM=2,MN=3,则BN的长为 .
15. 如图,在Rt△ABC中,∠C=90°,在△ABC外取点 D,E,使. 且α+β=∠B,连接DE.若AB=4,AC=3,则DE= .
16. 如图①,已知正方体. 的棱长为4cm,E,F,G分别是AB,AA ,AD 的中点,截面EFG将这个正方体切去一个角后得到一个新的几何体(如图②),则图②中阴影部分的面积为 cm .
三、解答题(共56分)
17. (8分)阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
18. (8分)如图,在四边形ABCD 中,∠DAB=30°,点E为AB的中点, 交AB于点E, ,BC=2,CD=4.
(1)求∠ABC的度数.
(2)求 CE的长.
19. (8分)如图,公路MN 和公路PQ 在点 P 处交汇,且. ,点A 处有一所中学, 160 m.若拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿 PN方向行驶时,
(1)学校是否会受到噪声影响 请说明理由.
(2)如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒
20. (10分)问题背景:在 中,AB,BC,AC三边的长分别为 求此三角形的面积.小辉同学在解答这道题时.先建立一个正方形网格(每个小正方形的边长为1).再在网格中画出格点. (即 三个顶点都在小正方形的顶点处),如图①所示.这样不需求 的高,而借用网格就能计算出它的面积.
(1)请你求出 的面积.
思维拓展:
(2)我们把上述求. 面积的方法叫做构图法.
如果 三边的长分别为 请利用图②的正方形网格(每个小正方形的边长为a)画出相应的. ,并求出它的面积.
探索创新:
(3)若 三边的长分别为 且 试运用构图法画出示意图并求出这三角形的面积.
21. (10分)通过对《勾股定理》的学习,我们知道:如果一个三角形中,两边的平方和等于第三边的平方,那么这个三角形一定是直角三角形.如果我们新定义一种三角形——两边的平方和等于第三边平方的2 倍的三角形叫做奇异三角形.
(1)根据奇异三角形的定义,请你判断:等边三角形一定是奇异三角形吗 (填“是”或“不是”).
(2)若某三角形的三边长分别为1, ,2,则该三角形是不是奇异三角形,请做出判断并写出判断依据.
(3)在 中,两边长分别为a,c,且 则这个三角形是不是奇异三角形 请做出判断并写出判断依据.
探究:在 Rt△ABC中, 且 若 是奇异三角形,求
22. (12 分)如图, 中, ,若点 P 从点 A 出发,以每秒1 个单位长度的速度沿折线 运动,设运动时间为t秒
(1)若点 P在AC上,且满足 时,求此时t的值.
(2)若点 P恰好在. 的平分线上,求t的值.
第十七章综合测试卷
1. B 2. C 3. B 4. B 5. D 6. A 7. D 8. A 9. D 10. B11. 5 12. 5 13. 10
14. 或 15. 5 16. 2
17. 解:当n=1时, ∵直角三角形有一边长为5,∴Ⅰ.当a=5时, 解得m (舍去);Ⅱ.当b=5时,即m=5,代入①③,得a=l2,c=13;Ⅲ. 当c=5时, 解得m=±3,∵m>0,∴m=3,代入①②,得a=4,b=3.综上所述,当n=1时,有一边长为5的直角三角形的另外两条边长分别为12,13或3,4.
18. 解:(1)如图,连接BD,∵ 点E为AB 的中点,DE⊥AB,∴BD=AD,AE=BE,
∵ ∠DAB = 30°,∴ ∠DBE = ∠DAB =
D 是直角三角形,且∠CBD=90°,
∴∠ABC=∠DBA+∠CBD=30°+90°=120°.
(2)如图,过点 C作CF⊥AB于点 F,则∠BFC=90°.
∵∠ABC=120°,∴∠BCF=30°,
∵ 在 Rt△BED 中,
19. 解:(1)如图,过点 A 作 AH⊥MN于点H,则∠AHP=90°,
在 Rt△APH中,∵∠HPA=30°,
∵80<100,
∴拖拉机在公路MN上沿PN方向行驶时学校会受到噪声影响.
(2)如图,假设拖拉机行驶到B点时开始影响学校,行驶到C点时结束对学校的影响,则AB=AC=100,∵AH⊥BC,∴BH=CH,在 Rt△ABH中,∠AHB=90°,AB=100,AH=80,
∴BC=2BH=120,
∵拖拉机的速度为18 km/h=5 m/s,
∴学校受到的影响的时间为: (秒).
20. 解:(1)△ABC的面积为:
(2)如图②,在边长为a的正方形网格中,△ABC即为所求作三角形,△ABC的面积为:
(3)如图③,在长为m、宽为n的网格中, 即为所求作三角形, 的面积为:
21. 解:(1)设等边三角形的边长为a,
∴等边三角形一定是奇异三角形.故答案为:是.
∴该三角形是奇异三角形.
(3)当c为斜边时, 不是奇异三角形;当b为斜边时,
是奇异三角形.
探究: 中,
是奇异三角形,
22. 解:(1)如图1,PA =PB,在 Rt△ACB 中,∠ACB = 由题得AP=t,则PB=t,PC=8-t,在 Rt△PCB中,由勾股定理得 解得 即当点P在AC上,且PA=PB时,t的值为
(2)分两种情况:①点P在BC上时,如图2所示,过点P作PE⊥AB于点E,则∠AEP=90°,
∵AP平分∠BAC,且PC⊥AC,
∴∠CAP=∠EAP,PE=PC,
在△ACP和△AEP中,
∴△ACP≌△AEP(AAS),∴AE=AC=8,∴BE=2,由题得PC=t-AC=t-8,则PE=t-8,PB=BC-PC=14-t,在 Rt△PEB 中,由勾股定理得 即 解得
②点P又回到A点时,∵AC+BC+AB=8+6+10=24,∴t=24.综上所述,点P在∠BAC的平分线上时,t的值为 或24.
