人教版数学八年级下册 18.1 平行四边形 &18.2.1 矩形 基础复习(一)(含答案)
文档属性
| 名称 | 人教版数学八年级下册 18.1 平行四边形 &18.2.1 矩形 基础复习(一)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 898.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 22:08:12 | ||
图片预览

文档简介
第十八章基础复习(一)
知识点 1 平行四边形
1. 平行四边形的性质:平行四边形的两组对边分别平行且相等;平行四边形的两组对角分别相等,邻角互补;平行四边形的对角线互相平分.
2. 两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
3. 平行四边形的判定:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
4. 三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线.三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
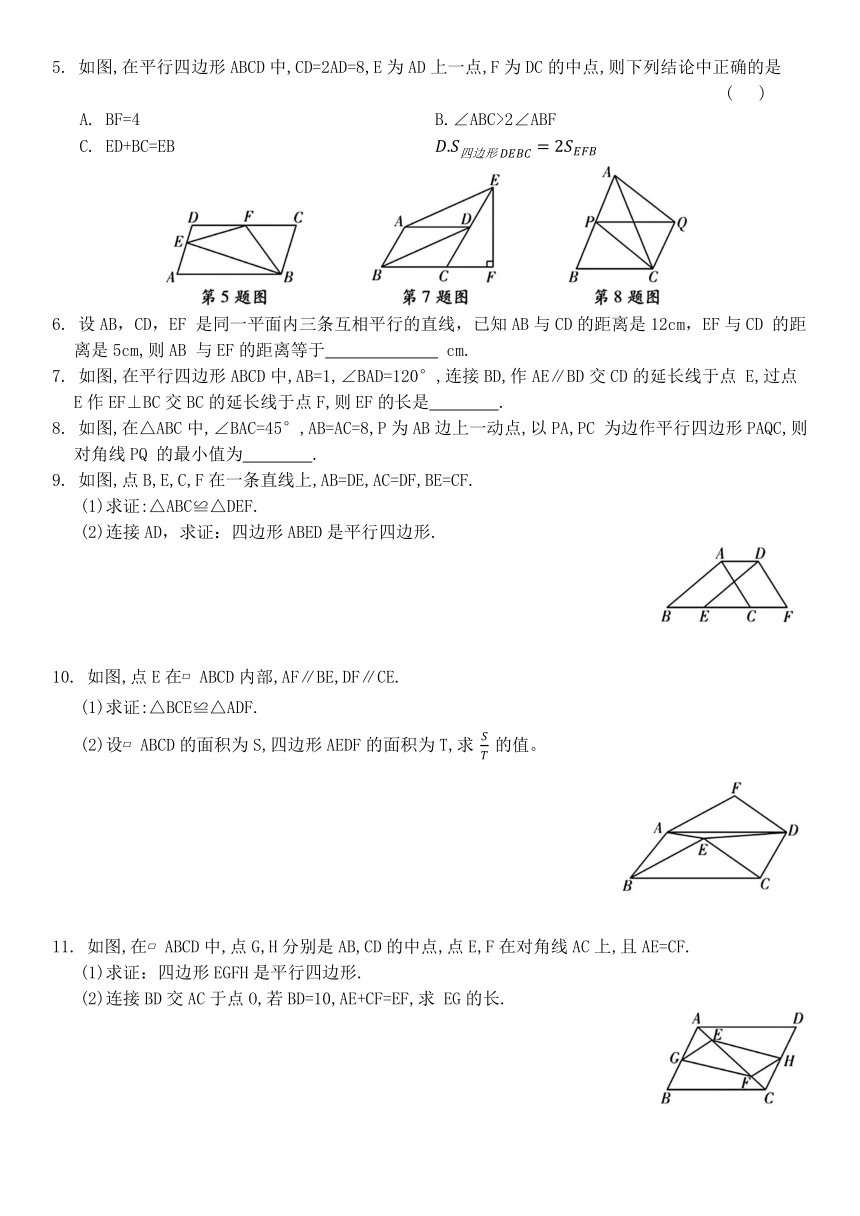
1. 如图,在△ABC中,. 点D 在AC边上,以CB,CD为边作 则∠E的度数为 ( )
A. 40° B. 50° C. 60° D. 70°
2. 如图,在四边形ABCD中,对角线AC和BD 相交于点O,下列条件不能判断四边形AB-CD 是平行四边形的是 ( )
B. AB=DC,AD=BC
D. OA=OC,OB=OD
3. 如图,在平面直角坐标系中, 的顶点坐标分别为A(3,a),B(2,2),C(b,3),D(8,6),则a+b的值为 ( )
A. 8 B. 9 C. 12 D. 11
4. 如图,已知△ABC中,. ,点E,D 分别在边AB,AC上,且BE=8,CD=10,点F,M,N分别是BC, BD,CE的中点,则MN的长为 ( )
B. 6 D. 3
5. 如图,在平行四边形ABCD中,CD=2AD=8,E为AD上一点,F为DC的中点,则下列结论中正确的是 ( )
A. BF=4 B.∠ABC>2∠ABF
C. ED+BC=EB
6. 设AB,CD,EF 是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD 的距离是5cm,则AB 与EF的距离等于 cm.
7. 如图,在平行四边形ABCD中,AB=1,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点 E,过点 E作EF⊥BC交BC的延长线于点F,则EF的长是 .
8. 如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA,PC 为边作平行四边形PAQC,则对角线PQ 的最小值为 .
9. 如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF.
(2)连接AD,求证:四边形ABED是平行四边形.
10. 如图,点E在 ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF.
(2)设 ABCD的面积为S,四边形AEDF的面积为T,求的值。
11. 如图,在 ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形.
(2)连接BD交AC于点O,若BD=10,AE+CF=EF,求 EG的长.
知识点 2 矩 形
1. 矩形的性质:四个角都是直角;对角线相等.
2. 直角三角形斜边上的中线等于斜边的一半.
3. 矩形的判定:有一个角是直角的平行四边形是矩形;有三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形.
12. 已知 ABCD的对角线AC,BD相交于点O,△AOD是等边三角形,且AD=4,则AB等于 ( )
A. 2 B. 4 D. 4
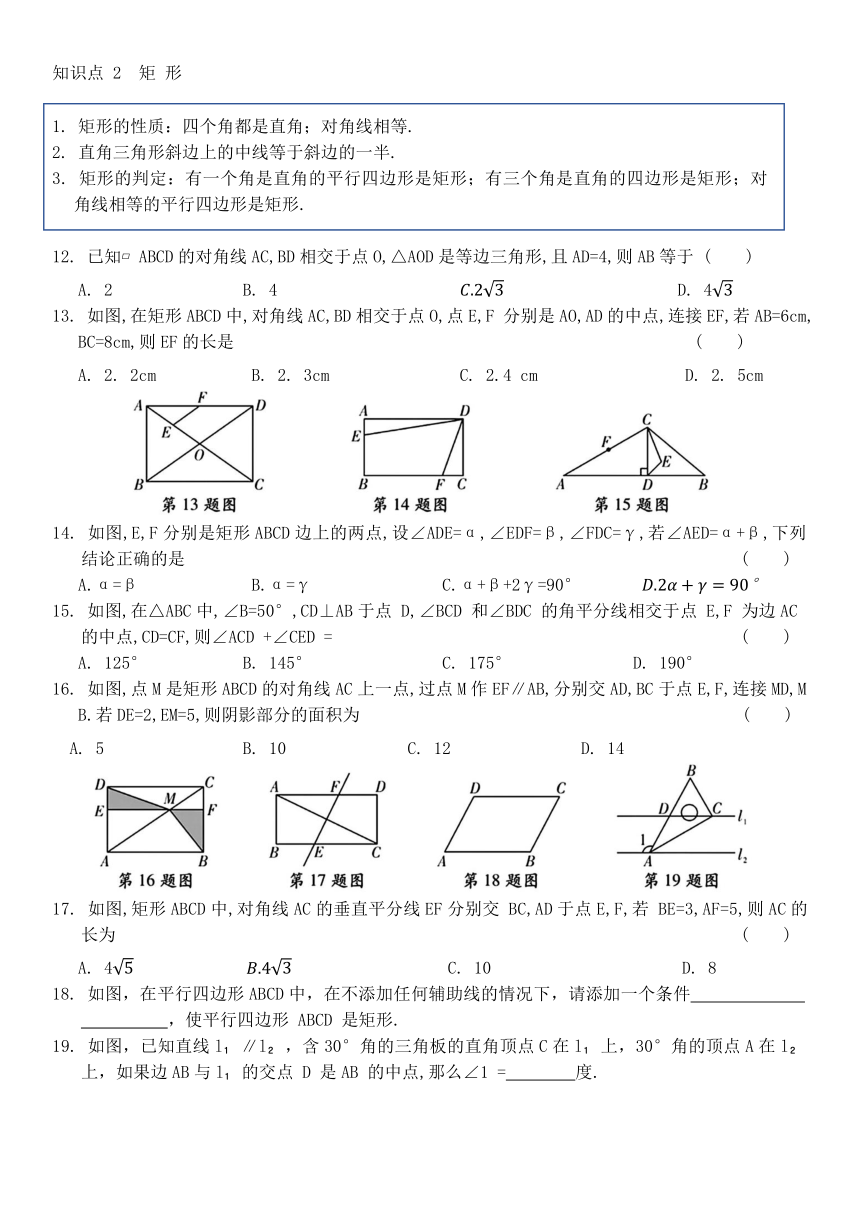
13. 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F 分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm,则EF的长是 ( )
A. 2. 2cm B. 2. 3cm C. 2.4 cm D. 2. 5cm
14. 如图,E,F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED=α+β,下列结论正确的是 ( )
A.α=β B.α=γ C.α+β+2γ=90°
15. 如图,在△ABC中,∠B=50°,CD⊥AB于点 D,∠BCD 和∠BDC 的角平分线相交于点 E,F 为边AC 的中点,CD=CF,则∠ACD +∠CED = ( )
A. 125° B. 145° C. 175° D. 190°
16. 如图,点M是矩形ABCD的对角线AC上一点,过点M作EF∥AB,分别交AD,BC于点E,F,连接MD,MB.若DE=2,EM=5,则阴影部分的面积为 ( )
A. 5 B. 10 C. 12 D. 14
17. 如图,矩形ABCD中,对角线AC的垂直平分线EF分别交 BC,AD于点E,F,若 BE=3,AF=5,则AC的长为 ( )
A. 4 C. 10 D. 8
18. 如图,在平行四边形ABCD中,在不添加任何辅助线的情况下,请添加一个条件 ,使平行四边形 ABCD 是矩形.
19. 如图,已知直线l ∥l ,含30°角的三角板的直角顶点C在l 上,30°角的顶点A在l 上,如果边AB与l 的交点 D 是AB 的中点,那么∠1 = 度.
20. 如图,矩形ABCD中,∠BAC=60°,以点A为圆心,以任意长为半径作弧分别交AB,AC于M,N两点,再分别以点 M,N为圆心,以大于 的长为半径作弧交于点 P,作射线AP交BC于点E,若BE=1,则矩形 ABCD 的面积等于 .
21. 如图,在 ABCD 中,E为 BC的中点,连接AE 并延长交 DC 的延长线于点 F,连接BF,AC.若AD=AF,求证:四边形ABFC是矩形.
22. 如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD 是矩形.
(2)若∠AOB:∠ODC=4:3,求∠ADO的度数.
23. 如图,在矩形ABCD中,AB=3,BC=4. M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)求证:△ABM≌△CDN.
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
第十八章基础复习(一)
1. D 2. C 3. C 4. A 5. D
6. 7或17 7. 8. 4
9. 证明:(1)∵BE=CF,∴BE+EC=EC+CF,即BC=EF,∵AB=DE,AC=DF,∴△ABC≌△DEF.
(2)由(1)知△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE,∵AB=DE,∴四边形ABED 是平行四边形.
10. (1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,
∴∠ABC+∠BAD=180°,即∠EBA+∠CBE+∠BAD=180°,
∵AF∥BE,∴∠EBA+∠BAF=180°,
即∠EBA+∠BAD+∠DAF=180°,
∴∠CBE=∠DAF,同理得∠BCE=∠ADF,
在△BCE和△ADF中,
∴△BCE≌△ADF(ASA).
(2)解:∵点E在 ABCD内部, 由(1)知:
∵ ABCD的面积为S,四边形AEDF的面积为 T,
11. (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,∴AG=CH,
∵AE=CF,∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,∴GE∥HF,又GE=HF,∴四边形EGFH是平行四边形.
(2)解:如图,连接BD交AC于点O,
∵ 四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=10,∴OB=OD=5,
∵AE=CF,OA=OC,∴OE=OF,
∵AE+CF=EF,∴2AE=EF=2OE,∴AE=OE,又点G是AB的中点,∴EG是△ABO的中位线,
12. D 13. D 14. B 15. C 16. B 17. A
18.∠ABC=90°(答案不唯一)
19. 120 20. 3
21. 证明:∵ 四边形ABCD是平行四边形,
∴AB∥DF,∴∠ABE=∠FCE,
∵E为BC的中点,∴BE=CE,
又∠AEB=∠FEC,∴△ABE≌△FCE,∴AE=FE,
又BE=CE,∴四边形ABFC是平行四边形,
在□ABCD中,AD=BC,
又AD=AF,∴BC=AF,∴平行四边形ABFC是矩形.
22. (1)证明:∵AO=OC,BO=OD,∴四边形ABCD是平行四边形,∵∠AOB=∠OAD+∠ODA=2∠OAD,∴∠OAD=∠ODA,∴AO=DO,∴AC=BD,∴四边形ABCD是矩形.
(2)解:∵四边形ABCD 是矩形,∴AB∥CD,∠BAD=90°,∴∠ABO=∠ODC,∵ ∠AOB:∠ODC =4:3,∴ ∠AOB:∠ABO =4:3,∵ OA=OB,∴∠ABO =∠BAO,∴∠BAO:∠AOB:∠ABO =3:4:3,∴∠ABO=54°,∵∠BAD=90°,∴∠ADO=90°-54°=36°.
23. (1)证明:∵ 四边形ABCD是矩形,∴AB=CD,AB∥CD,∴∠MAB=∠NCD,
在△ABM和△CDN中, ∴△ABM≌△CDN(SAS).
(2)解:如图,连接EF,交AC于点O.
∵ 四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ABC=90°,
∵E,F 分别是AD,BC 的中点,∴AE=BF=ED=CF,
又AE∥BF,∴四边形ABFE是矩形,∴EF=AB=3,在△AEO和△CFO中,
∴△AEO≌△CFO(AAS),
∴AG=OA-OG=1或AG=OA+OG=4,∴AG的长为1或4.
知识点 1 平行四边形
1. 平行四边形的性质:平行四边形的两组对边分别平行且相等;平行四边形的两组对角分别相等,邻角互补;平行四边形的对角线互相平分.
2. 两条平行线间的距离:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
3. 平行四边形的判定:两组对边分别平行的四边形是平行四边形;两组对边分别相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
4. 三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线.三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
1. 如图,在△ABC中,. 点D 在AC边上,以CB,CD为边作 则∠E的度数为 ( )
A. 40° B. 50° C. 60° D. 70°
2. 如图,在四边形ABCD中,对角线AC和BD 相交于点O,下列条件不能判断四边形AB-CD 是平行四边形的是 ( )
B. AB=DC,AD=BC
D. OA=OC,OB=OD
3. 如图,在平面直角坐标系中, 的顶点坐标分别为A(3,a),B(2,2),C(b,3),D(8,6),则a+b的值为 ( )
A. 8 B. 9 C. 12 D. 11
4. 如图,已知△ABC中,. ,点E,D 分别在边AB,AC上,且BE=8,CD=10,点F,M,N分别是BC, BD,CE的中点,则MN的长为 ( )
B. 6 D. 3
5. 如图,在平行四边形ABCD中,CD=2AD=8,E为AD上一点,F为DC的中点,则下列结论中正确的是 ( )
A. BF=4 B.∠ABC>2∠ABF
C. ED+BC=EB
6. 设AB,CD,EF 是同一平面内三条互相平行的直线,已知AB与CD的距离是12cm,EF与CD 的距离是5cm,则AB 与EF的距离等于 cm.
7. 如图,在平行四边形ABCD中,AB=1,∠BAD=120°,连接BD,作AE∥BD交CD的延长线于点 E,过点 E作EF⊥BC交BC的延长线于点F,则EF的长是 .
8. 如图,在△ABC中,∠BAC=45°,AB=AC=8,P为AB边上一动点,以PA,PC 为边作平行四边形PAQC,则对角线PQ 的最小值为 .
9. 如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF.
(2)连接AD,求证:四边形ABED是平行四边形.
10. 如图,点E在 ABCD内部,AF∥BE,DF∥CE.
(1)求证:△BCE≌△ADF.
(2)设 ABCD的面积为S,四边形AEDF的面积为T,求的值。
11. 如图,在 ABCD中,点G,H分别是AB,CD的中点,点E,F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形.
(2)连接BD交AC于点O,若BD=10,AE+CF=EF,求 EG的长.
知识点 2 矩 形
1. 矩形的性质:四个角都是直角;对角线相等.
2. 直角三角形斜边上的中线等于斜边的一半.
3. 矩形的判定:有一个角是直角的平行四边形是矩形;有三个角是直角的四边形是矩形;对角线相等的平行四边形是矩形.
12. 已知 ABCD的对角线AC,BD相交于点O,△AOD是等边三角形,且AD=4,则AB等于 ( )
A. 2 B. 4 D. 4
13. 如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F 分别是AO,AD的中点,连接EF,若AB=6cm,BC=8cm,则EF的长是 ( )
A. 2. 2cm B. 2. 3cm C. 2.4 cm D. 2. 5cm
14. 如图,E,F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED=α+β,下列结论正确的是 ( )
A.α=β B.α=γ C.α+β+2γ=90°
15. 如图,在△ABC中,∠B=50°,CD⊥AB于点 D,∠BCD 和∠BDC 的角平分线相交于点 E,F 为边AC 的中点,CD=CF,则∠ACD +∠CED = ( )
A. 125° B. 145° C. 175° D. 190°
16. 如图,点M是矩形ABCD的对角线AC上一点,过点M作EF∥AB,分别交AD,BC于点E,F,连接MD,MB.若DE=2,EM=5,则阴影部分的面积为 ( )
A. 5 B. 10 C. 12 D. 14
17. 如图,矩形ABCD中,对角线AC的垂直平分线EF分别交 BC,AD于点E,F,若 BE=3,AF=5,则AC的长为 ( )
A. 4 C. 10 D. 8
18. 如图,在平行四边形ABCD中,在不添加任何辅助线的情况下,请添加一个条件 ,使平行四边形 ABCD 是矩形.
19. 如图,已知直线l ∥l ,含30°角的三角板的直角顶点C在l 上,30°角的顶点A在l 上,如果边AB与l 的交点 D 是AB 的中点,那么∠1 = 度.
20. 如图,矩形ABCD中,∠BAC=60°,以点A为圆心,以任意长为半径作弧分别交AB,AC于M,N两点,再分别以点 M,N为圆心,以大于 的长为半径作弧交于点 P,作射线AP交BC于点E,若BE=1,则矩形 ABCD 的面积等于 .
21. 如图,在 ABCD 中,E为 BC的中点,连接AE 并延长交 DC 的延长线于点 F,连接BF,AC.若AD=AF,求证:四边形ABFC是矩形.
22. 如图,四边形ABCD中,对角线AC,BD相交于点O,AO=OC,BO=OD,且∠AOB=2∠OAD.
(1)求证:四边形ABCD 是矩形.
(2)若∠AOB:∠ODC=4:3,求∠ADO的度数.
23. 如图,在矩形ABCD中,AB=3,BC=4. M,N在对角线AC上,且AM=CN,E,F分别是AD,BC的中点.
(1)求证:△ABM≌△CDN.
(2)点G是对角线AC上的点,∠EGF=90°,求AG的长.
第十八章基础复习(一)
1. D 2. C 3. C 4. A 5. D
6. 7或17 7. 8. 4
9. 证明:(1)∵BE=CF,∴BE+EC=EC+CF,即BC=EF,∵AB=DE,AC=DF,∴△ABC≌△DEF.
(2)由(1)知△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE,∵AB=DE,∴四边形ABED 是平行四边形.
10. (1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,
∴∠ABC+∠BAD=180°,即∠EBA+∠CBE+∠BAD=180°,
∵AF∥BE,∴∠EBA+∠BAF=180°,
即∠EBA+∠BAD+∠DAF=180°,
∴∠CBE=∠DAF,同理得∠BCE=∠ADF,
在△BCE和△ADF中,
∴△BCE≌△ADF(ASA).
(2)解:∵点E在 ABCD内部, 由(1)知:
∵ ABCD的面积为S,四边形AEDF的面积为 T,
11. (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,∴AG=CH,
∵AE=CF,∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,∴GE∥HF,又GE=HF,∴四边形EGFH是平行四边形.
(2)解:如图,连接BD交AC于点O,
∵ 四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=10,∴OB=OD=5,
∵AE=CF,OA=OC,∴OE=OF,
∵AE+CF=EF,∴2AE=EF=2OE,∴AE=OE,又点G是AB的中点,∴EG是△ABO的中位线,
12. D 13. D 14. B 15. C 16. B 17. A
18.∠ABC=90°(答案不唯一)
19. 120 20. 3
21. 证明:∵ 四边形ABCD是平行四边形,
∴AB∥DF,∴∠ABE=∠FCE,
∵E为BC的中点,∴BE=CE,
又∠AEB=∠FEC,∴△ABE≌△FCE,∴AE=FE,
又BE=CE,∴四边形ABFC是平行四边形,
在□ABCD中,AD=BC,
又AD=AF,∴BC=AF,∴平行四边形ABFC是矩形.
22. (1)证明:∵AO=OC,BO=OD,∴四边形ABCD是平行四边形,∵∠AOB=∠OAD+∠ODA=2∠OAD,∴∠OAD=∠ODA,∴AO=DO,∴AC=BD,∴四边形ABCD是矩形.
(2)解:∵四边形ABCD 是矩形,∴AB∥CD,∠BAD=90°,∴∠ABO=∠ODC,∵ ∠AOB:∠ODC =4:3,∴ ∠AOB:∠ABO =4:3,∵ OA=OB,∴∠ABO =∠BAO,∴∠BAO:∠AOB:∠ABO =3:4:3,∴∠ABO=54°,∵∠BAD=90°,∴∠ADO=90°-54°=36°.
23. (1)证明:∵ 四边形ABCD是矩形,∴AB=CD,AB∥CD,∴∠MAB=∠NCD,
在△ABM和△CDN中, ∴△ABM≌△CDN(SAS).
(2)解:如图,连接EF,交AC于点O.
∵ 四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ABC=90°,
∵E,F 分别是AD,BC 的中点,∴AE=BF=ED=CF,
又AE∥BF,∴四边形ABFE是矩形,∴EF=AB=3,在△AEO和△CFO中,
∴△AEO≌△CFO(AAS),
∴AG=OA-OG=1或AG=OA+OG=4,∴AG的长为1或4.
