人教版数学八年级下册 18.2.2 菱形&18.2.3 正方形 基础复习(二)(含答案)
文档属性
| 名称 | 人教版数学八年级下册 18.2.2 菱形&18.2.3 正方形 基础复习(二)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1005.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-28 00:00:00 | ||
图片预览

文档简介
第十八章基础复习(二)
知识点 1 菱 形
1. 菱形的性质:菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
2. 菱形是轴对称图形,对称轴是两条对角线所在的直线.
3. 菱形的判定:有一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形.
1. 若菱形的周长为16,高为2.则菱形两邻角的度数之比为 ( )
A. 4:1 B. 5:1 C. 6:1 D. 7:1
2. 如图,在菱形ABCD中,AB=5,对角线AC与BD 相交于点O,且AC:BD=3:4,AE⊥CD 于点 E,则AE 的长是 ( )
A. 4 C. 5
3. 如图,在菱形ABCD中,点E为对角线AC上一点,且CE=CD,连接DE,若AB=5,AC=8,则 ( )
4. 如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形 AB-CD 为菱形的是 ( )
A. AC⊥BD B. AB =AD C. AC=BD D.∠ABD=∠CBD
5. 如图,菱形ABCD 的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A 到点 C 的方向平移,得到△A'B'O'.当点A'与点 C 重合时,点A与点 B'之间的距离为 ( )
A. 6 B. 8 C. 10 D. 12
6. 如图,在平面直角坐标系中,△ACE 是以菱形ABCD 的对角线AC 为边的等边三角形,AC=2,点 C与点 E 关于x轴对称,则点 D的坐标是 .
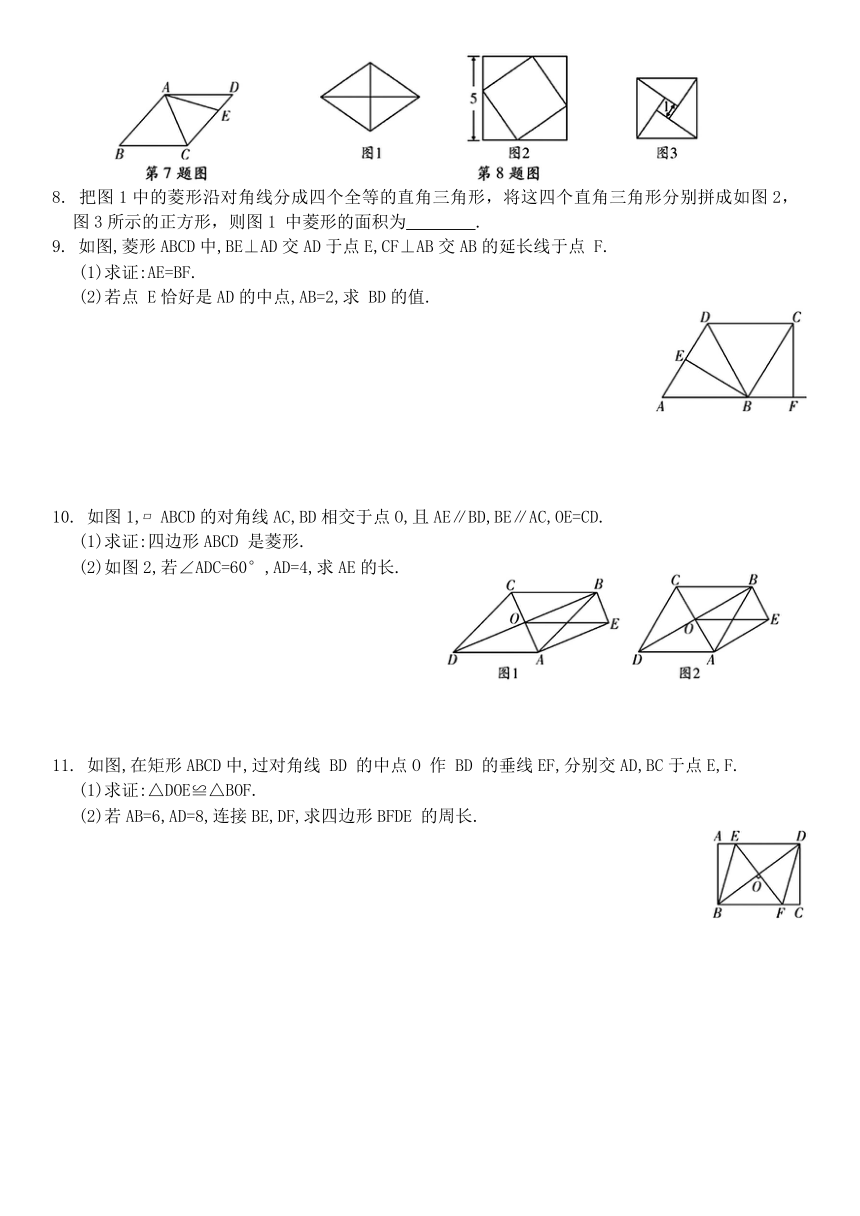
7. 如图,在菱形ABCD中,∠B=50°,点E在CD上,若AE=AC,则∠BAE= °.
8. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2, 图3所示的正方形,则图1 中菱形的面积为 .
9. 如图,菱形ABCD中,BE⊥AD交AD于点E,CF⊥AB交AB的延长线于点 F.
(1)求证:AE=BF.
(2)若点 E恰好是AD的中点,AB=2,求 BD的值.
10. 如图1, ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD 是菱形.
(2)如图2,若∠ADC=60°,AD=4,求AE的长.
11. 如图,在矩形ABCD中,过对角线 BD 的中点O 作 BD 的垂线EF,分别交AD,BC于点E,F.
(1)求证:△DOE≌△BOF.
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE 的周长.
知识点 2 正方形
1. 正方形的性质:对边平行,四条边都相等;四个角都是直角;对角线互相垂直平分且相等,每条对角线平分一组对角;正方形是轴对称图形,有四条对称轴.
2. 正方形的判定:有一组邻边相等的矩形是正方形;有一个角是直角的菱形是正方形.
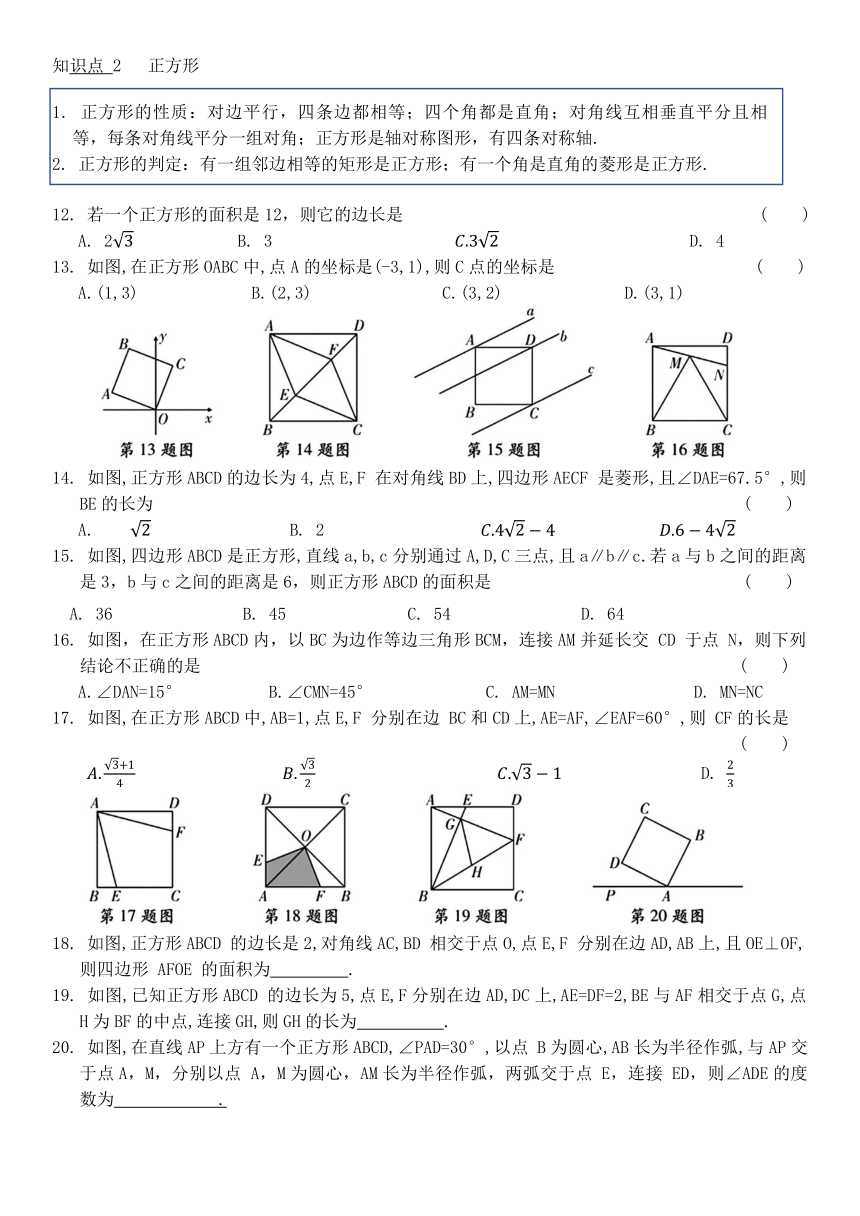
12. 若一个正方形的面积是12,则它的边长是 ( )
A. 2 B. 3 D. 4
13. 如图,在正方形OABC中,点A的坐标是(-3,1),则C点的坐标是 ( )
A.(1,3) B.(2,3) C.(3,2) D.(3,1)
14. 如图,正方形ABCD的边长为4,点E,F 在对角线BD上,四边形AECF 是菱形,且∠DAE=67.5°,则BE的长为 ( )
A. B. 2
15. 如图,四边形ABCD是正方形,直线a,b,c分别通过A,D,C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是 ( )
A. 36 B. 45 C. 54 D. 64
16. 如图,在正方形ABCD内,以BC为边作等边三角形BCM,连接AM并延长交 CD 于点 N,则下列结论不正确的是 ( )
A.∠DAN=15° B.∠CMN=45° C. AM=MN D. MN=NC
17. 如图,在正方形ABCD中,AB=1,点E,F 分别在边 BC和CD上,AE=AF,∠EAF=60°,则 CF的长是 ( )
D.
18. 如图,正方形ABCD 的边长是2,对角线AC,BD 相交于点O,点E,F 分别在边AD,AB上,且OE⊥OF,则四边形 AFOE 的面积为 .
19. 如图,已知正方形ABCD 的边长为5,点E,F分别在边AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
20. 如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点 B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点 A,M为圆心,AM长为半径作弧,两弧交于点 E,连接 ED,则∠ADE的度数为 .
21. 如图,在正方形 ABCD 中,点E是 BC上的一点,点 F 是 CD 延长线上的一点,且. 连接AE,AF,EF.
(1)求证:
(2)若 求 EF 的长.
22. 如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:
(2)求 的度数.
23. 如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且 ,过点 E作 交正方形外角的平分线 CG于点 G,连接GF.
求证:
(2)四边形 BEGF是平行四边形.
第十八章基础复习(二)
1. B 2. B 3. B 4. C 5. C 6.( ,0) 7. 115 8. 12
9. (1)证明:∵ 四边形 ABCD是菱形,
∴AB=BC,AD∥BC,∴∠A=∠CBF,
∵BE⊥AD,CF⊥AB,∴∠AEB=∠BFC=90°,
∴△AEB≌△BFC(AAS),∴AE=BF.
(2)解:∵E是AD中点,且BE⊥AD,
∴直线 BE为AD的垂直平分线,∴BD=AB=2.
10. (1)证明:∵AE∥BD,BE∥AC,∴四边形AEBO是平行四边形,
∵ 四边形ABCD是平行四边形,∴DC=AB,
∵OE=CD,∴OE=AB,∴平行四边形AEBO是矩形,
∴∠BOA=90°,∴AC⊥BD,∴平行四边形ABCD是菱形.
(2)解:由(1)知四边形 ABCD 是菱形,∴ AD = CD =4,∠ADO=∠CDO,
∴OE=CD=4,∵∠ADC=60°,∴∠ADO=30°,
由(1)知四边形AEBO是矩形,∴∠OAE=90°,
11. (1)证明:∵ 四边形ABCD是矩形,∴AD∥BC,
∴∠EDO=∠FBO.
∵O为BD的中点,∴DO=BO,又 在 和 中,
(2)解:由(1)可得,
∴ 四边形 BFDE是平行四边形,
又 ∴ 四边形 BFDE是菱形,
设
在 中,根据勾股定理可得,
即 解得
∴四边形 BFDE的周长
12. A 13. A 14. C 15. B 16. D 17. C
18. 1
20. 15°或
21. (1)证明:∵ 四边形ABCD是正方形,
在 和 中,
∴△ABE≌△ADF(SAS).
(2)解:∵△ABE≌△ADF,∴AE=AF,∠BAE=∠DAF,
∵∠BAE+∠EAD=90°,
∴∠DAF+∠EAF=90°,即∠EAF=90°,
22. (1)证明:∵ 四边形ABCD是正方形,
∴AB=CD,且∠BAD=∠CDA=90°,
∵△ADE是等边三角形,∴AE=DE,且∠EAD=∠EDA=60°,
∴∠BAE=∠BAD+∠EAD=150°,∠CDE=∠CDA+∠EDA=150°,
∴∠BAE=∠CDE,
在△BAE和△CDE中,
∴△BAE≌△CDE(SAS).
(2)解:∵AB=AD,且AD=AE,∴AB=AE,∴∠ABE=∠AEB.
由(1)知∠BAE=150°,∴∠AEB=(180°-150°)÷2=15°.
23. 证明:(1)∵ 四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,在△ABE和△BCF中,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,∴∠CBF=∠CEG,∴∠BAE=∠CEG,
∵∠BAE+∠BEA=90°,∴∠CEG+∠BEA=90°,
∴AE⊥EG,∴AE⊥BF.
(2)如图,延长AB至点 P,使BP=BE,连接EP,又AB=BC,∠ABE=90°,
∴AP=CE,∠EBP=90°,∴∠P=45°,
∵ CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,由(1)得∠BAE=∠CEG,
在△APE 和△ECG中,
∴△APE≌△ECG(ASA),∴AE=EG,
∵AE=BF,∴EG=BF, 又EG∥BF,∴四边形BEGF是平行四边形.
知识点 1 菱 形
1. 菱形的性质:菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
2. 菱形是轴对称图形,对称轴是两条对角线所在的直线.
3. 菱形的判定:有一组邻边相等的平行四边形是菱形;四条边都相等的四边形是菱形;对角线互相垂直的平行四边形是菱形.
1. 若菱形的周长为16,高为2.则菱形两邻角的度数之比为 ( )
A. 4:1 B. 5:1 C. 6:1 D. 7:1
2. 如图,在菱形ABCD中,AB=5,对角线AC与BD 相交于点O,且AC:BD=3:4,AE⊥CD 于点 E,则AE 的长是 ( )
A. 4 C. 5
3. 如图,在菱形ABCD中,点E为对角线AC上一点,且CE=CD,连接DE,若AB=5,AC=8,则 ( )
4. 如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形 AB-CD 为菱形的是 ( )
A. AC⊥BD B. AB =AD C. AC=BD D.∠ABD=∠CBD
5. 如图,菱形ABCD 的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A 到点 C 的方向平移,得到△A'B'O'.当点A'与点 C 重合时,点A与点 B'之间的距离为 ( )
A. 6 B. 8 C. 10 D. 12
6. 如图,在平面直角坐标系中,△ACE 是以菱形ABCD 的对角线AC 为边的等边三角形,AC=2,点 C与点 E 关于x轴对称,则点 D的坐标是 .
7. 如图,在菱形ABCD中,∠B=50°,点E在CD上,若AE=AC,则∠BAE= °.
8. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2, 图3所示的正方形,则图1 中菱形的面积为 .
9. 如图,菱形ABCD中,BE⊥AD交AD于点E,CF⊥AB交AB的延长线于点 F.
(1)求证:AE=BF.
(2)若点 E恰好是AD的中点,AB=2,求 BD的值.
10. 如图1, ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD 是菱形.
(2)如图2,若∠ADC=60°,AD=4,求AE的长.
11. 如图,在矩形ABCD中,过对角线 BD 的中点O 作 BD 的垂线EF,分别交AD,BC于点E,F.
(1)求证:△DOE≌△BOF.
(2)若AB=6,AD=8,连接BE,DF,求四边形BFDE 的周长.
知识点 2 正方形
1. 正方形的性质:对边平行,四条边都相等;四个角都是直角;对角线互相垂直平分且相等,每条对角线平分一组对角;正方形是轴对称图形,有四条对称轴.
2. 正方形的判定:有一组邻边相等的矩形是正方形;有一个角是直角的菱形是正方形.
12. 若一个正方形的面积是12,则它的边长是 ( )
A. 2 B. 3 D. 4
13. 如图,在正方形OABC中,点A的坐标是(-3,1),则C点的坐标是 ( )
A.(1,3) B.(2,3) C.(3,2) D.(3,1)
14. 如图,正方形ABCD的边长为4,点E,F 在对角线BD上,四边形AECF 是菱形,且∠DAE=67.5°,则BE的长为 ( )
A. B. 2
15. 如图,四边形ABCD是正方形,直线a,b,c分别通过A,D,C三点,且a∥b∥c.若a与b之间的距离是3,b与c之间的距离是6,则正方形ABCD的面积是 ( )
A. 36 B. 45 C. 54 D. 64
16. 如图,在正方形ABCD内,以BC为边作等边三角形BCM,连接AM并延长交 CD 于点 N,则下列结论不正确的是 ( )
A.∠DAN=15° B.∠CMN=45° C. AM=MN D. MN=NC
17. 如图,在正方形ABCD中,AB=1,点E,F 分别在边 BC和CD上,AE=AF,∠EAF=60°,则 CF的长是 ( )
D.
18. 如图,正方形ABCD 的边长是2,对角线AC,BD 相交于点O,点E,F 分别在边AD,AB上,且OE⊥OF,则四边形 AFOE 的面积为 .
19. 如图,已知正方形ABCD 的边长为5,点E,F分别在边AD,DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
20. 如图,在直线AP上方有一个正方形ABCD,∠PAD=30°,以点 B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点 A,M为圆心,AM长为半径作弧,两弧交于点 E,连接 ED,则∠ADE的度数为 .
21. 如图,在正方形 ABCD 中,点E是 BC上的一点,点 F 是 CD 延长线上的一点,且. 连接AE,AF,EF.
(1)求证:
(2)若 求 EF 的长.
22. 如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:
(2)求 的度数.
23. 如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且 ,过点 E作 交正方形外角的平分线 CG于点 G,连接GF.
求证:
(2)四边形 BEGF是平行四边形.
第十八章基础复习(二)
1. B 2. B 3. B 4. C 5. C 6.( ,0) 7. 115 8. 12
9. (1)证明:∵ 四边形 ABCD是菱形,
∴AB=BC,AD∥BC,∴∠A=∠CBF,
∵BE⊥AD,CF⊥AB,∴∠AEB=∠BFC=90°,
∴△AEB≌△BFC(AAS),∴AE=BF.
(2)解:∵E是AD中点,且BE⊥AD,
∴直线 BE为AD的垂直平分线,∴BD=AB=2.
10. (1)证明:∵AE∥BD,BE∥AC,∴四边形AEBO是平行四边形,
∵ 四边形ABCD是平行四边形,∴DC=AB,
∵OE=CD,∴OE=AB,∴平行四边形AEBO是矩形,
∴∠BOA=90°,∴AC⊥BD,∴平行四边形ABCD是菱形.
(2)解:由(1)知四边形 ABCD 是菱形,∴ AD = CD =4,∠ADO=∠CDO,
∴OE=CD=4,∵∠ADC=60°,∴∠ADO=30°,
由(1)知四边形AEBO是矩形,∴∠OAE=90°,
11. (1)证明:∵ 四边形ABCD是矩形,∴AD∥BC,
∴∠EDO=∠FBO.
∵O为BD的中点,∴DO=BO,又 在 和 中,
(2)解:由(1)可得,
∴ 四边形 BFDE是平行四边形,
又 ∴ 四边形 BFDE是菱形,
设
在 中,根据勾股定理可得,
即 解得
∴四边形 BFDE的周长
12. A 13. A 14. C 15. B 16. D 17. C
18. 1
20. 15°或
21. (1)证明:∵ 四边形ABCD是正方形,
在 和 中,
∴△ABE≌△ADF(SAS).
(2)解:∵△ABE≌△ADF,∴AE=AF,∠BAE=∠DAF,
∵∠BAE+∠EAD=90°,
∴∠DAF+∠EAF=90°,即∠EAF=90°,
22. (1)证明:∵ 四边形ABCD是正方形,
∴AB=CD,且∠BAD=∠CDA=90°,
∵△ADE是等边三角形,∴AE=DE,且∠EAD=∠EDA=60°,
∴∠BAE=∠BAD+∠EAD=150°,∠CDE=∠CDA+∠EDA=150°,
∴∠BAE=∠CDE,
在△BAE和△CDE中,
∴△BAE≌△CDE(SAS).
(2)解:∵AB=AD,且AD=AE,∴AB=AE,∴∠ABE=∠AEB.
由(1)知∠BAE=150°,∴∠AEB=(180°-150°)÷2=15°.
23. 证明:(1)∵ 四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,在△ABE和△BCF中,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,∴∠CBF=∠CEG,∴∠BAE=∠CEG,
∵∠BAE+∠BEA=90°,∴∠CEG+∠BEA=90°,
∴AE⊥EG,∴AE⊥BF.
(2)如图,延长AB至点 P,使BP=BE,连接EP,又AB=BC,∠ABE=90°,
∴AP=CE,∠EBP=90°,∴∠P=45°,
∵ CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,由(1)得∠BAE=∠CEG,
在△APE 和△ECG中,
∴△APE≌△ECG(ASA),∴AE=EG,
∵AE=BF,∴EG=BF, 又EG∥BF,∴四边形BEGF是平行四边形.
