人教版数学八年级下册 第十八章 平行四边形 综合测试卷(含答案)
文档属性
| 名称 | 人教版数学八年级下册 第十八章 平行四边形 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 07:36:27 | ||
图片预览



文档简介
第十八章综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 矩形具有而平行四边形不一定具有的性质是 ( )
A. 对边相等 B. 对角相等 C. 对角线相等 D. 对角线互相平分
2. (益阳中考)如图, ABCD 的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是 ( )
A. 10 B. 8 C. 7 D. 6
3. 如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB 于点 G,连接EF,则线段EF的长为 ( )
A. 1 B. C. D.
4. 如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点 E 的坐标为 ( )
A.(2, C.( ,3) D.(3,
5. 下面是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形. 下列推理过程正确的是 ( )
A. 由②推出③,由③推出① B. 由①推出②,由②推出③
C. 由③推出①,由①推出② D. 由①推出③,由③推出②
6. 如图,在□ABCD 中,按以下步骤作图:
①以点A为圆心,AB的长为半径作弧,交AD 于点 F;
②分别以点F,B为圆心,大于 FB的长为半径作弧,两弧在∠DAB 内交于点 G;
③作射线AG,交边BC于点 E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为 ( )
A. 12 B. 20 C. 24 D. 48
7. 如图,正方形ABCD的面积为144,菱形BCEF的面积为108,则 ( )
A. 18 B. 36 D. 36
8. 矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH= ( )
A. 1 B. 2/3
9. 如图,菱形ABCD 的边长为13,对角线AC=24,点E,F 分别是边CD,BC的中点,连接EF并延长与AB 的延长线相交于点 G,则EG= ( )
A. 13 B. 10 C. 12 D. 5
10. 如图,在正方形ABCD的对角线AC上取一点E.使得∠CDE=15°,连接BE并延长BE到F,使CF=CB,BF与CD相交于点H,若AB=1,有下列结论:①BE=DE;②CE+DE=EF;③S△DEC 则正确的结论的个数有 ( )
A. 3 个 B. 2个 C. 1 个 D. 0个
二、填空题(每小题4分,共24分)
11. 如图,已知在△ABC中,D,E分别是AB,AC的中点,F,G分别是AD,AE的中点,且FG=2cm,则 BC 的长度是 cm.
12. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
13. 如图,在菱形 ABCD 中,E,F 分别是AD,DC 的中点,若BD=4,EF =3,则菱形 ABCD 的周长为 .
14. 如图,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为点E,且AE平分∠BAC,则AB的长为 .
15. 如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作 DM⊥AB 于点M,DN⊥AC于点 N,连接MN,则线段MN的最小值为 .
16. 如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE,AF,EF,∠EAF=45°,BE=3,CF=4,则正方形的边长为 .
三、解答题(共56分)
17. (8分)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD, CF⊥BD,垂足分别为E,F,AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数.
(2)求证:AE=CF.
18. (8分)如图,菱形ABCD 的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB, OG∥EF.
(1)求证:四边形OEFG是矩形.
(2)若AD=10,EF=4,求OE 和BG的长.
19. (8分)如图,在△ABC中,AB=AC,点 D 是边AB的中点,DE∥BC 交AC于点E,连接BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH.
(2)当∠A为多少度时,FG⊥FH 并说明理由.
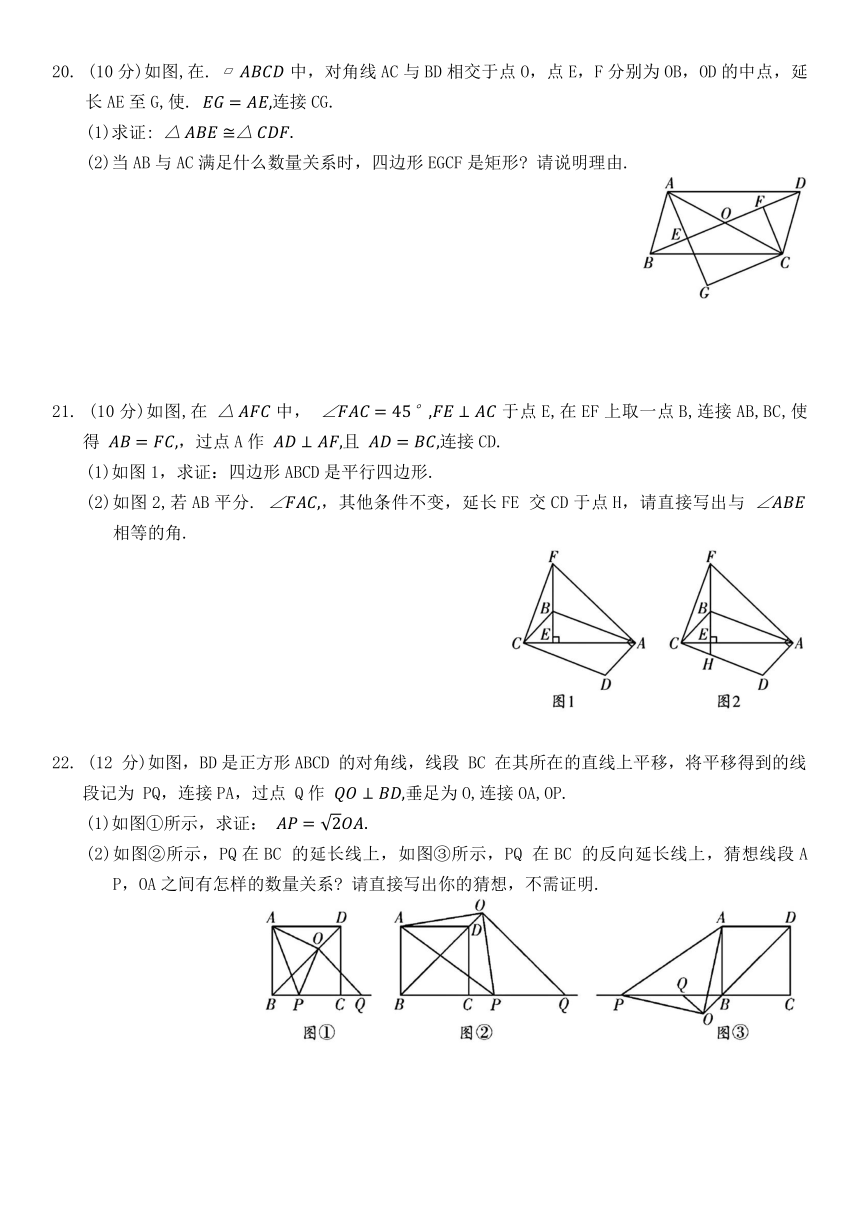
20. (10分)如图,在. 中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使. 连接CG.
(1)求证:
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形 请说明理由.
21. (10分)如图,在 中, 于点E,在EF上取一点B,连接AB,BC,使得 ,过点A作 且 连接CD.
(1)如图1,求证:四边形ABCD是平行四边形.
(2)如图2,若AB平分. ,其他条件不变,延长FE 交CD于点H,请直接写出与 相等的角.
22. (12 分)如图,BD是正方形ABCD 的对角线,线段 BC 在其所在的直线上平移,将平移得到的线段记为 PQ,连接PA,过点 Q作 垂足为O,连接OA,OP.
(1)如图①所示,求证:
(2)如图②所示,PQ在BC 的延长线上,如图③所示,PQ 在BC 的反向延长线上,猜想线段AP,OA之间有怎样的数量关系 请直接写出你的猜想,不需证明.
第十八章综合测试卷
1. C 2. D 3. C 4. D 5. A 6. C 7. C 8. C 9. B 10. A11. 8 12. 30
13. 4 16. 6
17. (1)解:∵AE⊥BD,∴∠AEO=90°,∵∠AOE=50°,∴∠EAO =40°,
又AC平分∠DAE,∴∠OAD =∠EAO=40°,
∵ 四边形ABCD是平行四边形,∴AD∥BC,
∴∠ACB=∠OAD=40°.
(2)证明:∵ 四边形ABCD是平行四边形,∴AO=CO,
∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°,
在△AEO 和△CFO中,
∴△AEO≌△CFO(AAS),∴AE=CF.
18. (1)证明:∵ 四边形ABCD是菱形,对角线AC与BD相交于点 O,∴点O为BD的中点,
又E是AD的中点,∴OE∥AB,
∵EF⊥AB,∴EF⊥OE.
又OG∥EF,∴OG⊥AB,∴四边形OEFG是矩形.
(2)解:∵ 四边形ABCD是菱形,∴AC⊥BD,
∵点E是AD的中点,且AD=10,
∵EF⊥AB,∴∠EFA=90°,
在 Rt△AEF中,EF=4,AE=5,
∵ 四边形ABCD为菱形,∴AB=AD=10,
∵ 四边形 OEFG为矩形,∴FG=OE=5,
∴BG=AB-AF--FG=10-3-5=2.
19. (1)证明:∵AB=AC,∴∠ABC=∠ACB,
∵ DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,∴AD=AE,∴DB=EC,
∵点F,G,H分别为BE,DE,BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
(2)解:当∠A=90°时,FG⊥FH.理由如下:如图,延长FG交AC于点N,
∵ FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,∴∠FNC=∠A,
∵∠A=90°,∴∠FNC=90°,即FN⊥AC,
∵FH∥AC,∴FG⊥FH,∴当∠A=90°时,FG⊥FH.
20. (1)证明:∵ 四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,.
∴BE=DF,在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
(2)解:当AC=2AB时,四边形EGCF是矩形.理由如下:
∵AC=2OA,AC=2AB,∴AB=OA,
∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,
同理:CF⊥OD,∴AG∥CF,即EG∥CF,
∵△ABE≌△CDF,∴AE=CF,
∵EG=AE,∴EG=CF,∴四边形EGCF是平行四边形,
∵∠OEG=90°,∴ 四边形 EGCF 是矩形.
21. (1)证明:∵FE⊥AC,∴∠FEA=∠FEC=90°,
∵∠FAC=45°,∴△AEF是等腰直角三角形,
∴AE=EF,∠AFE=∠FAE=45°,
在 Rt△AEB和Rt△FEC中,
∴Rt△AEB≌Rt△FEC(HL),∴BE=CE,∴∠CBE=∠BCE=45°,
∵AD⊥AF,∴∠FAD=90°,
∵∠FAC=45°,∴∠CAD=90°-45°=45°,
∴∠BCE=∠CAD,∴BC∥AD,又BC=AD,∴四边形ABCD是平行四边形.
(2)解:与∠ABE 相等的角有:∠CHB,∠BCD,∠BAD,∠FCA,∠CFA.理由如下:
由(1)得:Rt△AEB≌Rt△FEC,四边形ABCD是平行四边形,
∴∠BAE=∠CFE,∠FCE=∠ABE,∠BCH=∠BAD,AB∥CD,
∴∠CHB=∠ABE,∠BAE=∠DCA,
∵AB平分∠FAC,∠FAC=45°,∴∠BAC=∠BAF=22.5°,
∴∠ABE=90°-22.5°=67.5°,∠CFE=22.5°,∠DCA=22.5°,又∠AFH=∠BCE=∠CAD=45°,
∴∠CFA=∠BCD=∠BAD=67.5°,
∴∠CFA=∠BCD=∠BAD=∠ABE.
综上,与∠ABE相等的角为∠CHB,∠BCD,∠BAD,∠FCA,∠CFA.
22. (1)证明:∵四边形ABCD是正方形,∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠CBD=45°,∴OB=OQ,
∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,∴∠BOP+∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,.
(2)解:①当PQ在BC的延长线上时,线段PA,OA之间的数量关系为: 理由如下:
∵ 四边形ABCD是正方形,∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠CBD=45°,∴OB=OQ,
∵PQ=BC,∴AB=PQ,
在△ABO 和△PQO 中,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,∴∠BOP+∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,.
②当PQ 在 BC 的反向延长线上时,线段AP,OA之间的数量关系为: 理由如下:
∵四边形 ABCD 是正方形,∴AB = BC,∠ABC =90°,∠ABD =
∠CBD=45°,∴∠ABP=90°,∠OBQ=45°,∴∠ABO=135°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠OBQ=45°,
∴OB=OQ,∠PQO=135°,∴∠ABO=∠PQO,
∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP-∠POQ=90°,∴∠BOP-∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,∴
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 矩形具有而平行四边形不一定具有的性质是 ( )
A. 对边相等 B. 对角相等 C. 对角线相等 D. 对角线互相平分
2. (益阳中考)如图, ABCD 的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是 ( )
A. 10 B. 8 C. 7 D. 6
3. 如图,△ABC中,AB=4,AC=3,AD,AE分别是其角平分线和中线,过点C作CG⊥AD于点F,交AB 于点 G,连接EF,则线段EF的长为 ( )
A. 1 B. C. D.
4. 如图,在平面直角坐标系中,四边形OABC为菱形,O(0,0),A(4,0),∠AOC=60°,则对角线交点 E 的坐标为 ( )
A.(2, C.( ,3) D.(3,
5. 下面是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形. 下列推理过程正确的是 ( )
A. 由②推出③,由③推出① B. 由①推出②,由②推出③
C. 由③推出①,由①推出② D. 由①推出③,由③推出②
6. 如图,在□ABCD 中,按以下步骤作图:
①以点A为圆心,AB的长为半径作弧,交AD 于点 F;
②分别以点F,B为圆心,大于 FB的长为半径作弧,两弧在∠DAB 内交于点 G;
③作射线AG,交边BC于点 E,连接EF.若AB=5,BF=8,则四边形ABEF的面积为 ( )
A. 12 B. 20 C. 24 D. 48
7. 如图,正方形ABCD的面积为144,菱形BCEF的面积为108,则 ( )
A. 18 B. 36 D. 36
8. 矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH= ( )
A. 1 B. 2/3
9. 如图,菱形ABCD 的边长为13,对角线AC=24,点E,F 分别是边CD,BC的中点,连接EF并延长与AB 的延长线相交于点 G,则EG= ( )
A. 13 B. 10 C. 12 D. 5
10. 如图,在正方形ABCD的对角线AC上取一点E.使得∠CDE=15°,连接BE并延长BE到F,使CF=CB,BF与CD相交于点H,若AB=1,有下列结论:①BE=DE;②CE+DE=EF;③S△DEC 则正确的结论的个数有 ( )
A. 3 个 B. 2个 C. 1 个 D. 0个
二、填空题(每小题4分,共24分)
11. 如图,已知在△ABC中,D,E分别是AB,AC的中点,F,G分别是AD,AE的中点,且FG=2cm,则 BC 的长度是 cm.
12. 如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
13. 如图,在菱形 ABCD 中,E,F 分别是AD,DC 的中点,若BD=4,EF =3,则菱形 ABCD 的周长为 .
14. 如图,在矩形ABCD中,AD=8,对角线AC与BD相交于点O,AE⊥BD,垂足为点E,且AE平分∠BAC,则AB的长为 .
15. 如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作 DM⊥AB 于点M,DN⊥AC于点 N,连接MN,则线段MN的最小值为 .
16. 如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE,AF,EF,∠EAF=45°,BE=3,CF=4,则正方形的边长为 .
三、解答题(共56分)
17. (8分)如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作AE⊥BD, CF⊥BD,垂足分别为E,F,AC平分∠DAE.
(1)若∠AOE=50°,求∠ACB的度数.
(2)求证:AE=CF.
18. (8分)如图,菱形ABCD 的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB, OG∥EF.
(1)求证:四边形OEFG是矩形.
(2)若AD=10,EF=4,求OE 和BG的长.
19. (8分)如图,在△ABC中,AB=AC,点 D 是边AB的中点,DE∥BC 交AC于点E,连接BE,点F,G,H分别为BE,DE,BC的中点.
(1)求证:FG=FH.
(2)当∠A为多少度时,FG⊥FH 并说明理由.
20. (10分)如图,在. 中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使. 连接CG.
(1)求证:
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形 请说明理由.
21. (10分)如图,在 中, 于点E,在EF上取一点B,连接AB,BC,使得 ,过点A作 且 连接CD.
(1)如图1,求证:四边形ABCD是平行四边形.
(2)如图2,若AB平分. ,其他条件不变,延长FE 交CD于点H,请直接写出与 相等的角.
22. (12 分)如图,BD是正方形ABCD 的对角线,线段 BC 在其所在的直线上平移,将平移得到的线段记为 PQ,连接PA,过点 Q作 垂足为O,连接OA,OP.
(1)如图①所示,求证:
(2)如图②所示,PQ在BC 的延长线上,如图③所示,PQ 在BC 的反向延长线上,猜想线段AP,OA之间有怎样的数量关系 请直接写出你的猜想,不需证明.
第十八章综合测试卷
1. C 2. D 3. C 4. D 5. A 6. C 7. C 8. C 9. B 10. A11. 8 12. 30
13. 4 16. 6
17. (1)解:∵AE⊥BD,∴∠AEO=90°,∵∠AOE=50°,∴∠EAO =40°,
又AC平分∠DAE,∴∠OAD =∠EAO=40°,
∵ 四边形ABCD是平行四边形,∴AD∥BC,
∴∠ACB=∠OAD=40°.
(2)证明:∵ 四边形ABCD是平行四边形,∴AO=CO,
∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°,
在△AEO 和△CFO中,
∴△AEO≌△CFO(AAS),∴AE=CF.
18. (1)证明:∵ 四边形ABCD是菱形,对角线AC与BD相交于点 O,∴点O为BD的中点,
又E是AD的中点,∴OE∥AB,
∵EF⊥AB,∴EF⊥OE.
又OG∥EF,∴OG⊥AB,∴四边形OEFG是矩形.
(2)解:∵ 四边形ABCD是菱形,∴AC⊥BD,
∵点E是AD的中点,且AD=10,
∵EF⊥AB,∴∠EFA=90°,
在 Rt△AEF中,EF=4,AE=5,
∵ 四边形ABCD为菱形,∴AB=AD=10,
∵ 四边形 OEFG为矩形,∴FG=OE=5,
∴BG=AB-AF--FG=10-3-5=2.
19. (1)证明:∵AB=AC,∴∠ABC=∠ACB,
∵ DE∥BC,∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,∴AD=AE,∴DB=EC,
∵点F,G,H分别为BE,DE,BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
(2)解:当∠A=90°时,FG⊥FH.理由如下:如图,延长FG交AC于点N,
∵ FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,∴∠FNC=∠A,
∵∠A=90°,∴∠FNC=90°,即FN⊥AC,
∵FH∥AC,∴FG⊥FH,∴当∠A=90°时,FG⊥FH.
20. (1)证明:∵ 四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,.
∴BE=DF,在△ABE和△CDF中,
∴△ABE≌△CDF(SAS).
(2)解:当AC=2AB时,四边形EGCF是矩形.理由如下:
∵AC=2OA,AC=2AB,∴AB=OA,
∵E是OB的中点,∴AG⊥OB,∴∠OEG=90°,
同理:CF⊥OD,∴AG∥CF,即EG∥CF,
∵△ABE≌△CDF,∴AE=CF,
∵EG=AE,∴EG=CF,∴四边形EGCF是平行四边形,
∵∠OEG=90°,∴ 四边形 EGCF 是矩形.
21. (1)证明:∵FE⊥AC,∴∠FEA=∠FEC=90°,
∵∠FAC=45°,∴△AEF是等腰直角三角形,
∴AE=EF,∠AFE=∠FAE=45°,
在 Rt△AEB和Rt△FEC中,
∴Rt△AEB≌Rt△FEC(HL),∴BE=CE,∴∠CBE=∠BCE=45°,
∵AD⊥AF,∴∠FAD=90°,
∵∠FAC=45°,∴∠CAD=90°-45°=45°,
∴∠BCE=∠CAD,∴BC∥AD,又BC=AD,∴四边形ABCD是平行四边形.
(2)解:与∠ABE 相等的角有:∠CHB,∠BCD,∠BAD,∠FCA,∠CFA.理由如下:
由(1)得:Rt△AEB≌Rt△FEC,四边形ABCD是平行四边形,
∴∠BAE=∠CFE,∠FCE=∠ABE,∠BCH=∠BAD,AB∥CD,
∴∠CHB=∠ABE,∠BAE=∠DCA,
∵AB平分∠FAC,∠FAC=45°,∴∠BAC=∠BAF=22.5°,
∴∠ABE=90°-22.5°=67.5°,∠CFE=22.5°,∠DCA=22.5°,又∠AFH=∠BCE=∠CAD=45°,
∴∠CFA=∠BCD=∠BAD=67.5°,
∴∠CFA=∠BCD=∠BAD=∠ABE.
综上,与∠ABE相等的角为∠CHB,∠BCD,∠BAD,∠FCA,∠CFA.
22. (1)证明:∵四边形ABCD是正方形,∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠CBD=45°,∴OB=OQ,
∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,∴∠BOP+∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,.
(2)解:①当PQ在BC的延长线上时,线段PA,OA之间的数量关系为: 理由如下:
∵ 四边形ABCD是正方形,∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠CBD=45°,∴OB=OQ,
∵PQ=BC,∴AB=PQ,
在△ABO 和△PQO 中,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,∴∠BOP+∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,.
②当PQ 在 BC 的反向延长线上时,线段AP,OA之间的数量关系为: 理由如下:
∵四边形 ABCD 是正方形,∴AB = BC,∠ABC =90°,∠ABD =
∠CBD=45°,∴∠ABP=90°,∠OBQ=45°,∴∠ABO=135°,
∵QO⊥BD,∴∠BOQ=90°,∴∠BQO=∠OBQ=45°,
∴OB=OQ,∠PQO=135°,∴∠ABO=∠PQO,
∵PQ=BC,∴AB=PQ,
在△ABO和△PQO中,
∴△ABO≌△PQO(SAS),∴OA=OP,∠AOB=∠POQ,
∵∠BOP-∠POQ=90°,∴∠BOP-∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,∴
