人教版数学八年级下册 期中模拟综合测试卷(含答案)
文档属性
| 名称 | 人教版数学八年级下册 期中模拟综合测试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览




文档简介
期中模拟综合测试卷
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 下列各式是最简二次根式的是 ( )
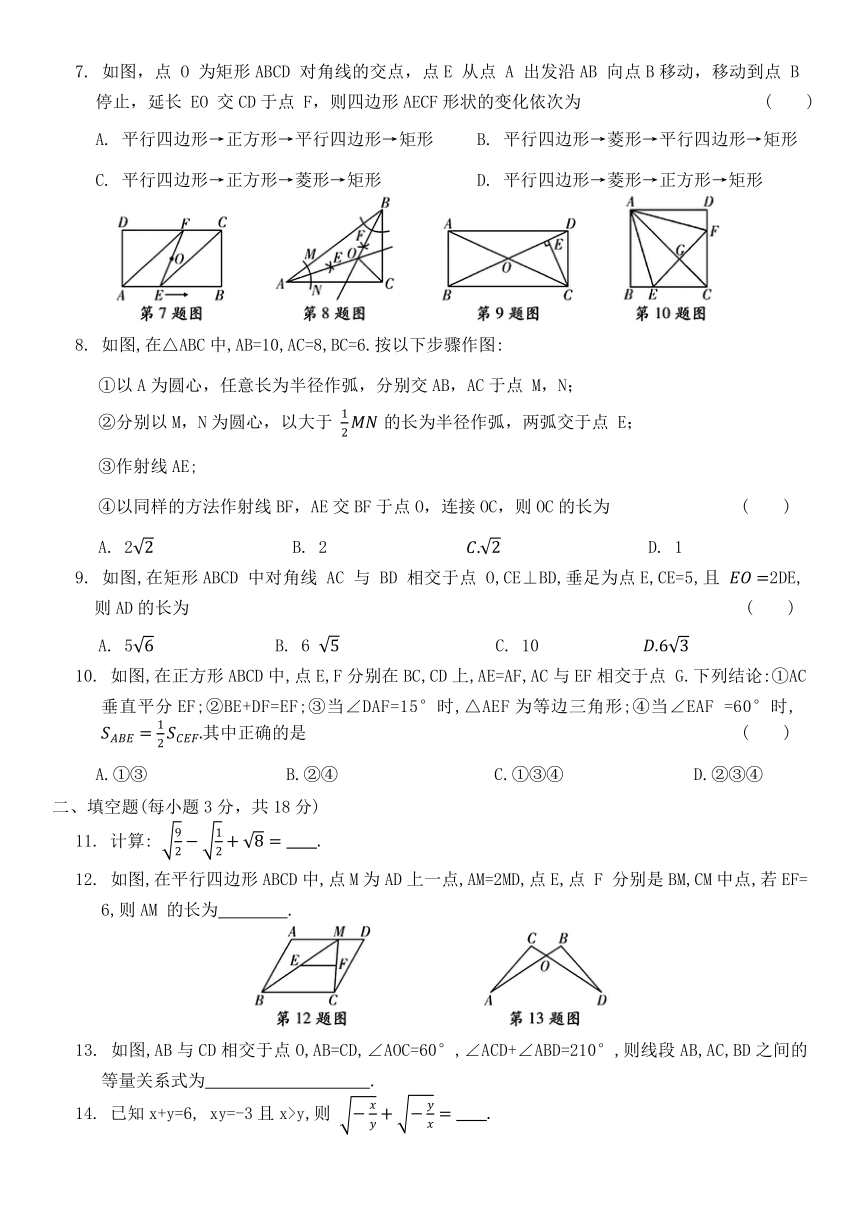
2. 如图,菱形ABCD中,∠D=150°,则∠1= ( )
A. 30° B. 25°
C. 20° D. 15°
3. 下列计算或运算中,正确的是 ( )
4. 如图,将矩形纸片ABCD 沿BE折叠,使点 A落在对角线BD上的A'处.若∠DBC=24°,则
∠A'EB等于 ( )
A. 66° B. 60° C. 57° D. 48°
5. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ( )
A. 直角三角形的面积 B. 最大正方形的面积
C. 较小两个正方形重叠部分的面积 D. 最大正方形与直角三角形的面积和
6. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点 C 和点 D距离门槛AB 都为1尺(1尺=10寸),则AB的长是 ( )
A. 50.5寸 B. 52寸 C. 101 寸 D. 104寸
7. 如图,点 O 为矩形ABCD 对角线的交点,点E 从点 A 出发沿AB 向点B移动,移动到点 B 停止,延长 EO 交CD于点 F,则四边形AECF形状的变化依次为 ( )
A. 平行四边形→正方形→平行四边形→矩形 B. 平行四边形→菱形→平行四边形→矩形
C. 平行四边形→正方形→菱形→矩形 D. 平行四边形→菱形→正方形→矩形
8. 如图,在△ABC中,AB=10,AC=8,BC=6.按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AC于点 M,N;
②分别以M,N为圆心,以大于 的长为半径作弧,两弧交于点 E;
③作射线AE;
④以同样的方法作射线BF,AE交BF于点O,连接OC,则OC的长为 ( )
A. 2 B. 2 D. 1
9. 如图,在矩形ABCD 中对角线 AC 与 BD 相交于点 O,CE⊥BD,垂足为点E,CE=5,且 2DE,则AD的长为 ( )
A. 5 B. 6 C. 10
10. 如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点 G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF =60°时, 其中正确的是 ( )
A.①③ B.②④ C.①③④ D.②③④
二、填空题(每小题3分,共18分)
11. 计算:
12. 如图,在平行四边形ABCD中,点M为AD上一点,AM=2MD,点E,点 F 分别是BM,CM中点,若EF=6,则AM 的长为 .
13. 如图,AB与CD相交于点O,AB=CD,∠AOC=60°,∠ACD+∠ABD=210°,则线段AB,AC,BD之间的等量关系式为 .
14. 已知x+y=6, xy=-3且x>y,则
15. 勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位: km).笔直铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为 km.
16. 如图,在菱形ABCD 中,对角线AC,BD 相交于点 O,点 E在线段BO上,连接AE,若CD=2BE,∠DAE=∠DEA,EO=1,则线段AE的长为 .
三、解答题(共72分)
17. (6分)计算:
18. (6分)如图,四边形ABCD是平行四边形, ,且分别交对角线AC于点 E,F,连接BE,DF.
(1)求证:AE=CF.
(2)若BE=DE,求证:四边形EBFD 为菱形.
19. (5分)在化简式子 时,李东的解答过程如下:
解:
(第一步)
(第二步)
.(第三步)
(1)李东的解答过程错在第 步.
(2)若其中 给出正确的化简过程,并求值.
20. (6分)如图,在菱形ABCD中,点E,F 分别是边AD,AB 的中点.
(1)求证:
(2)若 求菱形ABCD的面积.
21. (6分)观察下列各式及其验证过程:
验证:
验证:
(1)按照上述两个等式及其验证过程的基本思路,猜想 的变形结果并进行验证.
(2)针对上述各式反映的规律,写出用n(n为自然数,且 )表示的等式,并给出证明.
22. (9分)(1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图1,其中四个直角三角形较大的直角边长都为α,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为( 也可以表示为 所以 即 由此推导出重要勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则 图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)试用勾股定理解决以下问题:
如果直角三角形ABC的两直角边长为3 和4,则斜边上的高为 .
(3)试构造一个图形,使它的面积能够解释 画在下面的网格中,并标出字母a,b所表示的线段.
23. (8分)如图,菱形ABCD中,. ,点E,F分别在AB,AD上,且.
(1)求证: 为等边三角形.
(2)连接AC,若AC将四边形AECF的面积分为1:2 两部分,当 时,求 的面积.
24. (8分)在 中, ,如图①,若. 则有 若 为锐角三角形时,小明猜想: 理由如下:如图②,过点A作. 于点D,设 在 中, 在 中, 整理得 ∴ 当 为锐角三角形时, 小明的猜想是正确的.
(1)请你猜想,当 为钝角三角形时, 与 的大小关系.
(2)证明你猜想的结论是否正确.(温馨提示:在图③中,作BC边上的高)
25. (8分)如图,已知四边形ABCD为正方形, 点E为对角线AC上一动点,连接DE,过点 E 作 ,交BC于点F,以 DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)探究: 的值是否为定值 若是,请求出这个定值;若不是,请说明理由.
26. (10分)若 和 均为等腰三角形,且.
(1)如图1,点 B是DE的中点,判定四边形BEAC的形状,并说明理由.
(2)如图2,若点 G是EC的中点,连接 GB并延长至点F,使
求证:
期中模拟综合测试卷
1. A 2. D 3. B 4. C 5. C 6. C 7. B 8. A 9. A 10. C11. 3√2 12. 8
13. AB =AC + BD 14. 4 15.(1)20 (2)13 16. 2
17. 解:(1)原式
(2)原式
18. 证明:(1)如图,连接BD交AC于点O,
∵ 四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
又DE∥BF,∴∠DEO=∠BFO,
在△BOF和△DOE中,
∴△BOF≌△DOE(AAS),∴OF=OE,
∴AO-OE=CO-OF,∴AE=CF.
(2)由(1)可知,△BOF≌△DOE,∴BF=DE,∵ DE∥BF,∴四边形EBFD 是平行四边形.又 BE=DE,∴四边形 EBFD是菱形.
19. 解:(1)错在第二步.故答案为:二.
(2)原式 当 时,l-a<0,
∴原式
20. (1)证明:∵ 四边形ABCD是菱形,∴AB=AD,
∵点E,F 分别是AD,AB的中点,
在△ABE和△ADF中
(2)解:如图,连接BD,
∵四边形ABCD是菱形,∴∠A=∠C=60°,
AD=AB,∴△ABD是等边三角形,
∵E是AD的中点,∴BE⊥AD,
在 Rt△AEB中,∵∠A=60°,
由勾股定理得
解得AB=2,∴AD=AB=2,∴S菱形.
21. 解:
验 证:
(n为自然数,且n≥2).
证明如下:
22. 解:(1)梯形ABCD的面积可以表示为 也可以表示为 即
(2)∵直角三角形的两直角边分别为3,4,∴斜边为5,设斜边上的高为h,则 解得 故答案为:
(3)∵图形面积为:
∴该图形的边长为( ,由此可画出的图形为:
23. 解:(1)证明:如图,连接AC,
∵ 四边形ABCD是菱形,
又
和 都是等边三角形,
在 和 中, ∴△CBE≌△CAF(SAS),∴CE=CF,∠BCE=∠ACF,
∵∠BCE+∠ACE=∠ACB=60°,∴∠FCA+∠ACE=60°,
∴∠ECF=60°,∴△ECF为等边三角形.
(2)由(1)可知
∴= , 过点A作AH⊥BC交BC于点H,
如图,则∠AHB=90°,在△ABH中,∵∠B=60°,∴∠BAH=30°,
当 时, 的面积
当 时, 的面积 =
综上,△BEC的面积为: 或
24. (1)解:当△ABC为钝角三角形时, 与 的大小关系为:
(2)证明:如图,过点 A 作 AD⊥BC于点 D,设CD=x,
在 Rt△ADC中,
在 Rt△ADB 中,
即当△ABC为钝角三角形时,( 25. (1)证明:如图,过点E作EM⊥BC于M,EN⊥CD于点 N,则∠DNE=∠FME=90°,
∵ 四边形 ABCD是正方形,
∴∠BCD=90°,∴∠MEN=90°,
∵ 点 E 是正方形ABCD对角线上的点,
∴EM=EN,
∵ 四边形 DEFG是矩形,∴∠DEF=90°,∴∠DEN=∠MEF,
在△DEN和△FEM中,
∴△DEN≌△FEM(ASA),∴EF=DE,
∵ 四边形DEFG是矩形,∴矩形DEFG是正方形.
(2)解:CE+CG的值是定值,定值为6.理由如下:
∵ 四边形ABCD和四边形 DEFG是正方形,
∵ DE=DG,AD=DC,∠ADC=∠EDG=90°,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,
在△ADE 和△CDG中,
∴△ADE≌△CDG(SAS),∴AE=CG,
∴CE+CG=CE+AE=AC= AB= 3 =6,
∴CE+CG的值是定值6.
26. (1)解:四边形BEAC是平行四边形.理由如下:
∵ △EAD为等腰三角形且∠EAD=90°,∴∠E=45°,
∵B是DE的中点,∴AB⊥DE,∴∠BAE=45°,
∵△ABC是等腰三角形且∠BAC=90°,∴∠CBA=45°,
∴∠BAE=∠CBA,∴BC∥EA,又AB⊥DE,∴∠EBA=∠BAC=90°,
∴BE∥AC,
∴ 四边形 BEAC 是平行四边形.
(2)证明:①∵△AED和△ABC为等腰三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=90°,
∴∠EAD+∠DAB=∠BAC+∠DAB,
即∠EAB=∠DAC,
∴△AEB≌△ADC(SAS).
∴EB=DC.
②如图,延长 FG至点H,使GH=FG.
∵G是EC的中点,∴EG=CG,又∠EGH=∠CGF,∴△EHG≌△CFG.
∴∠BFC=∠H,CF=EH,
∵CF=CD,BE=CD,∴BE=CF,
∴BE=EH,∴∠EBG=∠H,∴∠EBG=∠BFC.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题3分,共30分)
1. 下列各式是最简二次根式的是 ( )
2. 如图,菱形ABCD中,∠D=150°,则∠1= ( )
A. 30° B. 25°
C. 20° D. 15°
3. 下列计算或运算中,正确的是 ( )
4. 如图,将矩形纸片ABCD 沿BE折叠,使点 A落在对角线BD上的A'处.若∠DBC=24°,则
∠A'EB等于 ( )
A. 66° B. 60° C. 57° D. 48°
5. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ( )
A. 直角三角形的面积 B. 最大正方形的面积
C. 较小两个正方形重叠部分的面积 D. 最大正方形与直角三角形的面积和
6. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点 C 和点 D距离门槛AB 都为1尺(1尺=10寸),则AB的长是 ( )
A. 50.5寸 B. 52寸 C. 101 寸 D. 104寸
7. 如图,点 O 为矩形ABCD 对角线的交点,点E 从点 A 出发沿AB 向点B移动,移动到点 B 停止,延长 EO 交CD于点 F,则四边形AECF形状的变化依次为 ( )
A. 平行四边形→正方形→平行四边形→矩形 B. 平行四边形→菱形→平行四边形→矩形
C. 平行四边形→正方形→菱形→矩形 D. 平行四边形→菱形→正方形→矩形
8. 如图,在△ABC中,AB=10,AC=8,BC=6.按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AC于点 M,N;
②分别以M,N为圆心,以大于 的长为半径作弧,两弧交于点 E;
③作射线AE;
④以同样的方法作射线BF,AE交BF于点O,连接OC,则OC的长为 ( )
A. 2 B. 2 D. 1
9. 如图,在矩形ABCD 中对角线 AC 与 BD 相交于点 O,CE⊥BD,垂足为点E,CE=5,且 2DE,则AD的长为 ( )
A. 5 B. 6 C. 10
10. 如图,在正方形ABCD中,点E,F分别在BC,CD上,AE=AF,AC与EF相交于点 G.下列结论:①AC垂直平分EF;②BE+DF=EF;③当∠DAF=15°时,△AEF为等边三角形;④当∠EAF =60°时, 其中正确的是 ( )
A.①③ B.②④ C.①③④ D.②③④
二、填空题(每小题3分,共18分)
11. 计算:
12. 如图,在平行四边形ABCD中,点M为AD上一点,AM=2MD,点E,点 F 分别是BM,CM中点,若EF=6,则AM 的长为 .
13. 如图,AB与CD相交于点O,AB=CD,∠AOC=60°,∠ACD+∠ABD=210°,则线段AB,AC,BD之间的等量关系式为 .
14. 已知x+y=6, xy=-3且x>y,则
15. 勘测队按实际需要构建了平面直角坐标系,并标示了A,B,C三地的坐标,数据如图(单位: km).笔直铁路经过A,B两地.
(1)A,B间的距离为 km.
(2)计划修一条从C到铁路AB的最短公路l,并在l上建一个维修站D,使D到A,C的距离相等,则C,D间的距离为 km.
16. 如图,在菱形ABCD 中,对角线AC,BD 相交于点 O,点 E在线段BO上,连接AE,若CD=2BE,∠DAE=∠DEA,EO=1,则线段AE的长为 .
三、解答题(共72分)
17. (6分)计算:
18. (6分)如图,四边形ABCD是平行四边形, ,且分别交对角线AC于点 E,F,连接BE,DF.
(1)求证:AE=CF.
(2)若BE=DE,求证:四边形EBFD 为菱形.
19. (5分)在化简式子 时,李东的解答过程如下:
解:
(第一步)
(第二步)
.(第三步)
(1)李东的解答过程错在第 步.
(2)若其中 给出正确的化简过程,并求值.
20. (6分)如图,在菱形ABCD中,点E,F 分别是边AD,AB 的中点.
(1)求证:
(2)若 求菱形ABCD的面积.
21. (6分)观察下列各式及其验证过程:
验证:
验证:
(1)按照上述两个等式及其验证过程的基本思路,猜想 的变形结果并进行验证.
(2)针对上述各式反映的规律,写出用n(n为自然数,且 )表示的等式,并给出证明.
22. (9分)(1)教材在探索平方差公式时利用了面积法,面积法可以帮助我们直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图1,其中四个直角三角形较大的直角边长都为α,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为( 也可以表示为 所以 即 由此推导出重要勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则 图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)试用勾股定理解决以下问题:
如果直角三角形ABC的两直角边长为3 和4,则斜边上的高为 .
(3)试构造一个图形,使它的面积能够解释 画在下面的网格中,并标出字母a,b所表示的线段.
23. (8分)如图,菱形ABCD中,. ,点E,F分别在AB,AD上,且.
(1)求证: 为等边三角形.
(2)连接AC,若AC将四边形AECF的面积分为1:2 两部分,当 时,求 的面积.
24. (8分)在 中, ,如图①,若. 则有 若 为锐角三角形时,小明猜想: 理由如下:如图②,过点A作. 于点D,设 在 中, 在 中, 整理得 ∴ 当 为锐角三角形时, 小明的猜想是正确的.
(1)请你猜想,当 为钝角三角形时, 与 的大小关系.
(2)证明你猜想的结论是否正确.(温馨提示:在图③中,作BC边上的高)
25. (8分)如图,已知四边形ABCD为正方形, 点E为对角线AC上一动点,连接DE,过点 E 作 ,交BC于点F,以 DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)探究: 的值是否为定值 若是,请求出这个定值;若不是,请说明理由.
26. (10分)若 和 均为等腰三角形,且.
(1)如图1,点 B是DE的中点,判定四边形BEAC的形状,并说明理由.
(2)如图2,若点 G是EC的中点,连接 GB并延长至点F,使
求证:
期中模拟综合测试卷
1. A 2. D 3. B 4. C 5. C 6. C 7. B 8. A 9. A 10. C11. 3√2 12. 8
13. AB =AC + BD 14. 4 15.(1)20 (2)13 16. 2
17. 解:(1)原式
(2)原式
18. 证明:(1)如图,连接BD交AC于点O,
∵ 四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
又DE∥BF,∴∠DEO=∠BFO,
在△BOF和△DOE中,
∴△BOF≌△DOE(AAS),∴OF=OE,
∴AO-OE=CO-OF,∴AE=CF.
(2)由(1)可知,△BOF≌△DOE,∴BF=DE,∵ DE∥BF,∴四边形EBFD 是平行四边形.又 BE=DE,∴四边形 EBFD是菱形.
19. 解:(1)错在第二步.故答案为:二.
(2)原式 当 时,l-a<0,
∴原式
20. (1)证明:∵ 四边形ABCD是菱形,∴AB=AD,
∵点E,F 分别是AD,AB的中点,
在△ABE和△ADF中
(2)解:如图,连接BD,
∵四边形ABCD是菱形,∴∠A=∠C=60°,
AD=AB,∴△ABD是等边三角形,
∵E是AD的中点,∴BE⊥AD,
在 Rt△AEB中,∵∠A=60°,
由勾股定理得
解得AB=2,∴AD=AB=2,∴S菱形.
21. 解:
验 证:
(n为自然数,且n≥2).
证明如下:
22. 解:(1)梯形ABCD的面积可以表示为 也可以表示为 即
(2)∵直角三角形的两直角边分别为3,4,∴斜边为5,设斜边上的高为h,则 解得 故答案为:
(3)∵图形面积为:
∴该图形的边长为( ,由此可画出的图形为:
23. 解:(1)证明:如图,连接AC,
∵ 四边形ABCD是菱形,
又
和 都是等边三角形,
在 和 中, ∴△CBE≌△CAF(SAS),∴CE=CF,∠BCE=∠ACF,
∵∠BCE+∠ACE=∠ACB=60°,∴∠FCA+∠ACE=60°,
∴∠ECF=60°,∴△ECF为等边三角形.
(2)由(1)可知
∴= , 过点A作AH⊥BC交BC于点H,
如图,则∠AHB=90°,在△ABH中,∵∠B=60°,∴∠BAH=30°,
当 时, 的面积
当 时, 的面积 =
综上,△BEC的面积为: 或
24. (1)解:当△ABC为钝角三角形时, 与 的大小关系为:
(2)证明:如图,过点 A 作 AD⊥BC于点 D,设CD=x,
在 Rt△ADC中,
在 Rt△ADB 中,
即当△ABC为钝角三角形时,( 25. (1)证明:如图,过点E作EM⊥BC于M,EN⊥CD于点 N,则∠DNE=∠FME=90°,
∵ 四边形 ABCD是正方形,
∴∠BCD=90°,∴∠MEN=90°,
∵ 点 E 是正方形ABCD对角线上的点,
∴EM=EN,
∵ 四边形 DEFG是矩形,∴∠DEF=90°,∴∠DEN=∠MEF,
在△DEN和△FEM中,
∴△DEN≌△FEM(ASA),∴EF=DE,
∵ 四边形DEFG是矩形,∴矩形DEFG是正方形.
(2)解:CE+CG的值是定值,定值为6.理由如下:
∵ 四边形ABCD和四边形 DEFG是正方形,
∵ DE=DG,AD=DC,∠ADC=∠EDG=90°,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,
在△ADE 和△CDG中,
∴△ADE≌△CDG(SAS),∴AE=CG,
∴CE+CG=CE+AE=AC= AB= 3 =6,
∴CE+CG的值是定值6.
26. (1)解:四边形BEAC是平行四边形.理由如下:
∵ △EAD为等腰三角形且∠EAD=90°,∴∠E=45°,
∵B是DE的中点,∴AB⊥DE,∴∠BAE=45°,
∵△ABC是等腰三角形且∠BAC=90°,∴∠CBA=45°,
∴∠BAE=∠CBA,∴BC∥EA,又AB⊥DE,∴∠EBA=∠BAC=90°,
∴BE∥AC,
∴ 四边形 BEAC 是平行四边形.
(2)证明:①∵△AED和△ABC为等腰三角形,
∴AE=AD,AB=AC,∠EAD=∠BAC=90°,
∴∠EAD+∠DAB=∠BAC+∠DAB,
即∠EAB=∠DAC,
∴△AEB≌△ADC(SAS).
∴EB=DC.
②如图,延长 FG至点H,使GH=FG.
∵G是EC的中点,∴EG=CG,又∠EGH=∠CGF,∴△EHG≌△CFG.
∴∠BFC=∠H,CF=EH,
∵CF=CD,BE=CD,∴BE=CF,
∴BE=EH,∴∠EBG=∠H,∴∠EBG=∠BFC.
同课章节目录
