人教版数学八年级下册 19.2.2-19.3 基础复习(二)(含答案)
文档属性
| 名称 | 人教版数学八年级下册 19.2.2-19.3 基础复习(二)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 541.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 08:48:42 | ||
图片预览


文档简介
第十九章基础复习(二)
知识点 1 一次函数
1. 一次函数:一般地,形如y= kx+b(k,b是常数,k≠0)的函数,叫做一次函数,特别地,当b=0时,y= kx+b为y= kx,所以说正比例函数是一种特殊的一次函数.
2. 性质:当k>0时,图象左低右高,y随x的增大而增大;当k<0时,图象左高右低,y随x的增大而减小.
3. 待定系数法求解析式:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
1. 若点 P 在一次函数y=-x+4的图象上,则点 P 一定不在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 直线y=3x+1向下平移2个单位,所得直线的解析式是 ( )
A. y=3x+3 B. y=3x-2 C. y=3x+2 D. y=3x-1
是一次函数y=5x-3图象上的两点,则下列判断正确的是 ( )
C. 当 时, D. 当. 时,
4. 在平面直角坐标系中,已知函数y= ax+a(a≠0)的图象过点 P(1,2),则该函数的图象可能是 ( )
5. 一条直线与x轴的正半轴、y轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点 P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数解析式是 ( )
A. y= -x+4 B. y=x+4 C. y=x+8 D. y= -x+8
6. 如图,一次函数 的图象与x轴,y轴分别交于点A,B,过点B的直线l平分△ABO的面积,则直线l相应的函数解析式为 ( )
7. 已知点A(a,b)在直线y=-3x+5上,则6a+2b-1的值为 .
8. 在平面直角坐标系中,点. 到直线 的距离公式为: 则点 到直线 的距离为 .
9. 函数 的图象与x轴、y轴分别交于A,B两点,点C在x轴上.若 为等腰三角形,则满足条件的点 C 共有 个.
10. 已知
(1)化简 P.
(2)若点(a,b)在一次函数 的图象上,求P 的值.
11. 如图,一次函数 的图象与y轴交于点A,一次函数y 的图象与y轴交于点B(0,6),点 C 为两函数图象交点,且点 C 的横坐标为2.
(1)求一次函数, 的函数解析式.
(2)求 的面积.
(3)在坐标轴上,是否存在一点P,使得 请直接写出点 P 的坐标.
知识点 2 一次函数与方程、不等式
1. 一次函数与一元一次方程的关系:由于任何一个以x为未知数的一元一次方程都可以转化为 (a,b为常数, 的形式,所以解一元一次方程可以转化为:当某个一次函数 的函数值为0时,求自变量x的值.
2. 一次函数与一元一次不等式:因为任何一个以x为未知数的一元一次不等式都可以转化为 (或 (a,b为常数, 的形式,则解一元一次不等式可以看作:当一次函数的函数值大于0(或小于0)时,求自变量x的取值范围.
3. 一次函数与二元一次方程(组):①一般地,因为每个含有未知数x和γ的二元一次方程都可以转化为 的形式,所以每个二元一次方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
②一般地,每个二元一次方程组都对应两个一次函数,于是也对应两条直线.
③从“数”的角度看,解方程组就是求使两个函数值相等的自变量的值以及此时的函数值.
④从“形”的角度看,解方程组就是确定两条直线的交点坐标.
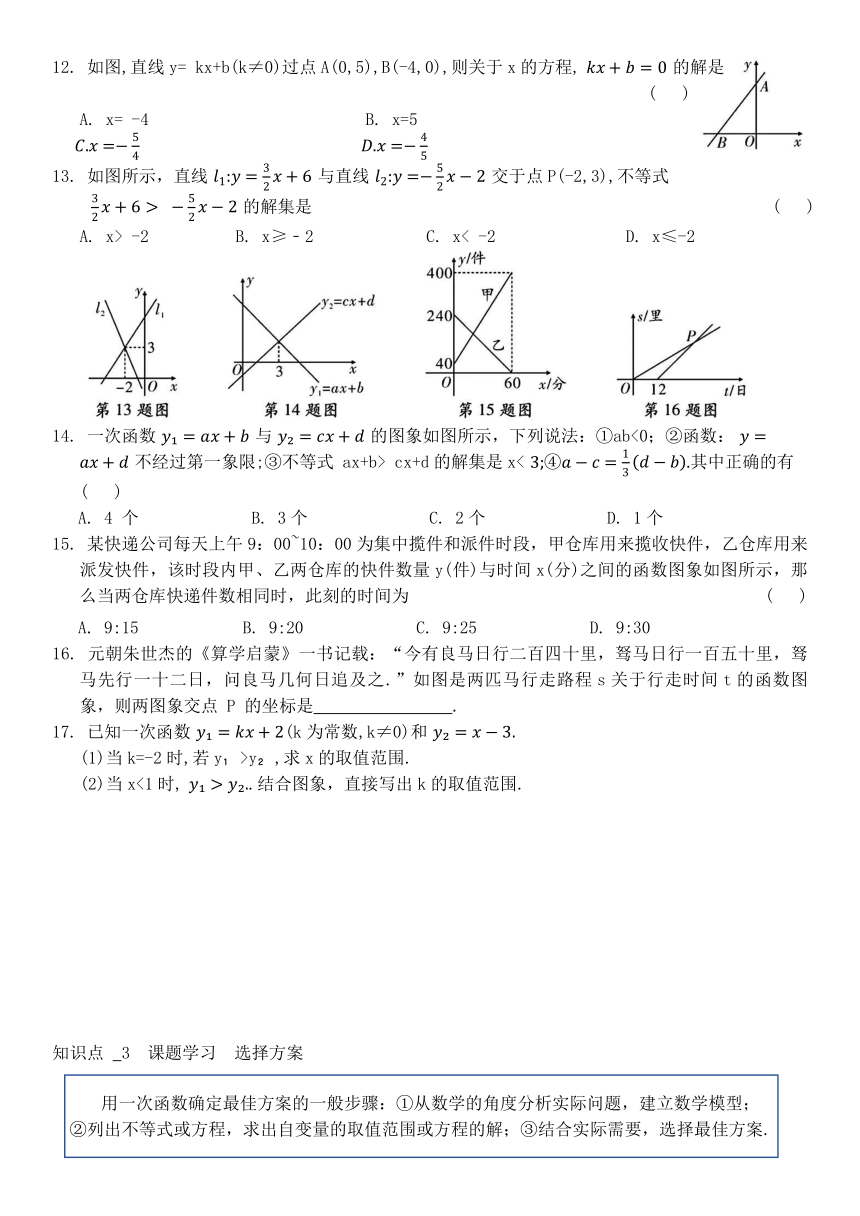
12. 如图,直线y= kx+b(k≠0)过点A(0,5),B(-4,0),则关于x的方程, 的解是
( )
A. x= -4 B. x=5
13. 如图所示,直线 与直线 交于点P(-2,3),不等式
的解集是 ( )
A. x> -2 B. x≥﹣2 C. x< -2 D. x≤-2
14. 一次函数 与 的图象如图所示,下列说法:①ab<0;②函数: 不经过第一象限;③不等式 ax+b> cx+d的解集是x< 其中正确的有 ( )
A. 4 个 B. 3个 C. 2个 D. 1个
15. 某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )
A. 9:15 B. 9:20 C. 9:25 D. 9:30
16. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点 P 的坐标是 .
17. 已知一次函数 (k为常数,k≠0)和
(1)当k=-2时,若y >y ,求x的取值范围.
(2)当x<1时, .结合图象,直接写出k的取值范围.
知识点 3 课题学习 选择方案
用一次函数确定最佳方案的一般步骤:①从数学的角度分析实际问题,建立数学模型;
②列出不等式或方程,求出自变量的取值范围或方程的解;③结合实际需要,选择最佳方案.
18. 某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为x张,购票总价为γ元).方案一:购票总价由图中的折线OAB所表示的函数关系确定;方案二:提供8000 元赞助后,每张票的票价为50元.则两种方案购票总价相同时,x的值为 ( )
A. 80 B. 120 C. 160 D. 200
19. 在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达B地后,停留3秒卸货,然后原路返回A地,慢车到达A地即停运休息,如图表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a,b的值分别为 ( )
A. 39,26 B. 39,26.4 C. 38,26 D. 38,26.4
20. 一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离s( km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B 两村相距10km;②出发1.25h后两人相遇;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了15min或65 min时两人相距2 km.其中正确的个数是 ( )
A. 1 个 B. 2 个 C. 3 个 D. 4个
21. 某商店今年6月初销售纯净水的数量如下表所示:
日期 l 2 3 4
数量(瓶) 120 125 130 135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为 瓶.
22. 某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480 元购买 B 款保温杯的数量与用360 元购买 A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元
第十九章基础复习(二)
1. C 2. D 3. D 4. A 5. A 6. D 7. 9 9. 4
10. 解:
(2)∵点(a,b)在一次函数 的图象上,
11. 解:(1)当 时,y =2x﹣2=2,∴C(2,2),设 把B(0,6),C(2,2)代入可得 解得 一次函数 的函数解析式为
(2)对于一次函数 令 则
①当P在y轴上时, 即 又A(0,-2),∴P(0,14)或 ②当P在x轴上时,设直线 的图象与x轴交于点D,令 则 l 又D(1,0),∴P(-7,0)或(9,0).综上,在坐标轴上,存在一点 P,使得 此时P点的坐标为(0,14)或(0,-18)或( -7,0)或(9,0).
12. A 13. A 14. A 15. B 16.(32,4800)
17. 解:(1)k=-2时, 根据题意得-2x+2>x-3,解得
(2)当x=1时, 把(1,-2)代入 得k+2 =-2,解得k=-4;当直线 2 与直线 平行时,k=1,一次函数y=-4x+2,y=x+2和 的图象如图,由图可知,当-4≤k<0时, 当018. D 19. B 20. D 21. 150
22. 解:(1)设A款保温杯的销售单价为x元,则B款保温杯的销售单价为(x+10)元,根据题意可得 解得x=30,经检验x=30是原方程的解且符合实际,∴x+10=40.
答:A款保温杯的销售单价为 30 元,B款保温杯的销售单价为40元.
(2)设购进B款保温杯的数量为y个,则购进A款保温杯的数量为 个,由题意得, 解得
设销售利润为w,则根据题意可得
∵6>0,∴w随y的增大而增大,
∴当 时,w有最大值,最大值为1 440.
答:当购进B款保温杯的数量为40个,A款保温杯的数量为80个时销售利润最大,最大利润为1 440 元.
知识点 1 一次函数
1. 一次函数:一般地,形如y= kx+b(k,b是常数,k≠0)的函数,叫做一次函数,特别地,当b=0时,y= kx+b为y= kx,所以说正比例函数是一种特殊的一次函数.
2. 性质:当k>0时,图象左低右高,y随x的增大而增大;当k<0时,图象左高右低,y随x的增大而减小.
3. 待定系数法求解析式:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
1. 若点 P 在一次函数y=-x+4的图象上,则点 P 一定不在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 直线y=3x+1向下平移2个单位,所得直线的解析式是 ( )
A. y=3x+3 B. y=3x-2 C. y=3x+2 D. y=3x-1
是一次函数y=5x-3图象上的两点,则下列判断正确的是 ( )
C. 当 时, D. 当. 时,
4. 在平面直角坐标系中,已知函数y= ax+a(a≠0)的图象过点 P(1,2),则该函数的图象可能是 ( )
5. 一条直线与x轴的正半轴、y轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点 P 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数解析式是 ( )
A. y= -x+4 B. y=x+4 C. y=x+8 D. y= -x+8
6. 如图,一次函数 的图象与x轴,y轴分别交于点A,B,过点B的直线l平分△ABO的面积,则直线l相应的函数解析式为 ( )
7. 已知点A(a,b)在直线y=-3x+5上,则6a+2b-1的值为 .
8. 在平面直角坐标系中,点. 到直线 的距离公式为: 则点 到直线 的距离为 .
9. 函数 的图象与x轴、y轴分别交于A,B两点,点C在x轴上.若 为等腰三角形,则满足条件的点 C 共有 个.
10. 已知
(1)化简 P.
(2)若点(a,b)在一次函数 的图象上,求P 的值.
11. 如图,一次函数 的图象与y轴交于点A,一次函数y 的图象与y轴交于点B(0,6),点 C 为两函数图象交点,且点 C 的横坐标为2.
(1)求一次函数, 的函数解析式.
(2)求 的面积.
(3)在坐标轴上,是否存在一点P,使得 请直接写出点 P 的坐标.
知识点 2 一次函数与方程、不等式
1. 一次函数与一元一次方程的关系:由于任何一个以x为未知数的一元一次方程都可以转化为 (a,b为常数, 的形式,所以解一元一次方程可以转化为:当某个一次函数 的函数值为0时,求自变量x的值.
2. 一次函数与一元一次不等式:因为任何一个以x为未知数的一元一次不等式都可以转化为 (或 (a,b为常数, 的形式,则解一元一次不等式可以看作:当一次函数的函数值大于0(或小于0)时,求自变量x的取值范围.
3. 一次函数与二元一次方程(组):①一般地,因为每个含有未知数x和γ的二元一次方程都可以转化为 的形式,所以每个二元一次方程都对应一个一次函数,于是也对应一条直线.这条直线上每个点的坐标(x,y)都是这个二元一次方程的解.
②一般地,每个二元一次方程组都对应两个一次函数,于是也对应两条直线.
③从“数”的角度看,解方程组就是求使两个函数值相等的自变量的值以及此时的函数值.
④从“形”的角度看,解方程组就是确定两条直线的交点坐标.
12. 如图,直线y= kx+b(k≠0)过点A(0,5),B(-4,0),则关于x的方程, 的解是
( )
A. x= -4 B. x=5
13. 如图所示,直线 与直线 交于点P(-2,3),不等式
的解集是 ( )
A. x> -2 B. x≥﹣2 C. x< -2 D. x≤-2
14. 一次函数 与 的图象如图所示,下列说法:①ab<0;②函数: 不经过第一象限;③不等式 ax+b> cx+d的解集是x< 其中正确的有 ( )
A. 4 个 B. 3个 C. 2个 D. 1个
15. 某快递公司每天上午9:00~10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )
A. 9:15 B. 9:20 C. 9:25 D. 9:30
16. 元朝朱世杰的《算学启蒙》一书记载:“今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何日追及之.”如图是两匹马行走路程s关于行走时间t的函数图象,则两图象交点 P 的坐标是 .
17. 已知一次函数 (k为常数,k≠0)和
(1)当k=-2时,若y >y ,求x的取值范围.
(2)当x<1时, .结合图象,直接写出k的取值范围.
知识点 3 课题学习 选择方案
用一次函数确定最佳方案的一般步骤:①从数学的角度分析实际问题,建立数学模型;
②列出不等式或方程,求出自变量的取值范围或方程的解;③结合实际需要,选择最佳方案.
18. 某市体育馆将举办明星足球赛,为此体育馆推出两种团体购票方案(设购票张数为x张,购票总价为γ元).方案一:购票总价由图中的折线OAB所表示的函数关系确定;方案二:提供8000 元赞助后,每张票的票价为50元.则两种方案购票总价相同时,x的值为 ( )
A. 80 B. 120 C. 160 D. 200
19. 在“加油向未来”电视节目中,王清和李北进行无人驾驶汽车运送货物表演,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达B地后,停留3秒卸货,然后原路返回A地,慢车到达A地即停运休息,如图表示的是两车之间的距离y(米)与行驶时间x(秒)的函数图象,根据图象信息,计算a,b的值分别为 ( )
A. 39,26 B. 39,26.4 C. 38,26 D. 38,26.4
20. 一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离s( km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B 两村相距10km;②出发1.25h后两人相遇;③甲每小时比乙多骑行8km;④相遇后,乙又骑行了15min或65 min时两人相距2 km.其中正确的个数是 ( )
A. 1 个 B. 2 个 C. 3 个 D. 4个
21. 某商店今年6月初销售纯净水的数量如下表所示:
日期 l 2 3 4
数量(瓶) 120 125 130 135
观察此表,利用所学函数知识预测今年6月7日该商店销售纯净水的数量约为 瓶.
22. 某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480 元购买 B 款保温杯的数量与用360 元购买 A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B款保温杯数量的两倍.若A款保温杯的销售单价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元
第十九章基础复习(二)
1. C 2. D 3. D 4. A 5. A 6. D 7. 9 9. 4
10. 解:
(2)∵点(a,b)在一次函数 的图象上,
11. 解:(1)当 时,y =2x﹣2=2,∴C(2,2),设 把B(0,6),C(2,2)代入可得 解得 一次函数 的函数解析式为
(2)对于一次函数 令 则
①当P在y轴上时, 即 又A(0,-2),∴P(0,14)或 ②当P在x轴上时,设直线 的图象与x轴交于点D,令 则 l 又D(1,0),∴P(-7,0)或(9,0).综上,在坐标轴上,存在一点 P,使得 此时P点的坐标为(0,14)或(0,-18)或( -7,0)或(9,0).
12. A 13. A 14. A 15. B 16.(32,4800)
17. 解:(1)k=-2时, 根据题意得-2x+2>x-3,解得
(2)当x=1时, 把(1,-2)代入 得k+2 =-2,解得k=-4;当直线 2 与直线 平行时,k=1,一次函数y=-4x+2,y=x+2和 的图象如图,由图可知,当-4≤k<0时, 当0
22. 解:(1)设A款保温杯的销售单价为x元,则B款保温杯的销售单价为(x+10)元,根据题意可得 解得x=30,经检验x=30是原方程的解且符合实际,∴x+10=40.
答:A款保温杯的销售单价为 30 元,B款保温杯的销售单价为40元.
(2)设购进B款保温杯的数量为y个,则购进A款保温杯的数量为 个,由题意得, 解得
设销售利润为w,则根据题意可得
∵6>0,∴w随y的增大而增大,
∴当 时,w有最大值,最大值为1 440.
答:当购进B款保温杯的数量为40个,A款保温杯的数量为80个时销售利润最大,最大利润为1 440 元.
