24.2.2直线和圆的位置关系(第3课时) 课件(共35张PPT)——初中数学人教版(2012)九年级上册
文档属性
| 名称 | 24.2.2直线和圆的位置关系(第3课时) 课件(共35张PPT)——初中数学人教版(2012)九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 39.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览






文档简介
(共35张PPT)
24.2.2直线和圆的位置关系(第3课时)
人教版(2012)九年级上册
学习目录
Part One
壹
学习目录
了解切线长的定义及切线长定理
1
会运用切线长定理进行计算与证明
2
认识三角形的内切圆及其有关概念,会作一个三角形的内切圆,掌握内心的性质
3
探索新知
Part Two
贰
知识回顾
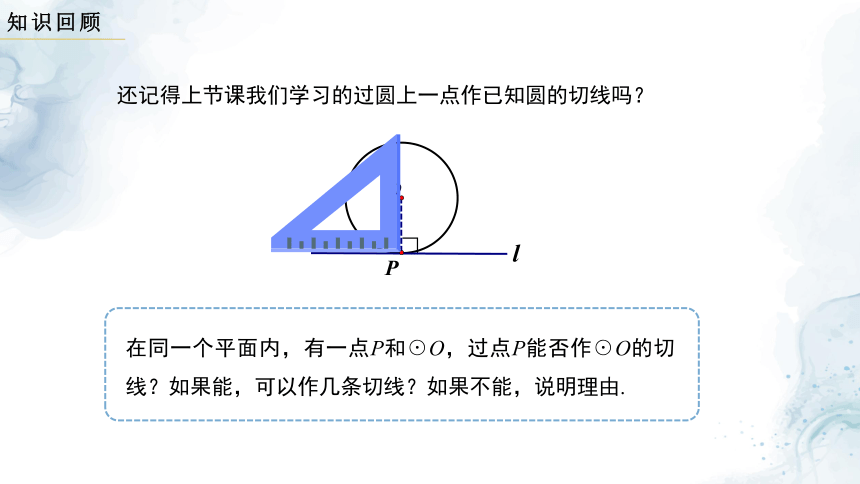
还记得上节课我们学习的过圆上一点作已知圆的切线吗?
∟
o
P
l
在同一个平面内,有一点P和☉O,过点P能否作☉O的切线?如果能,可以作几条切线?如果不能,说明理由.
知识回顾
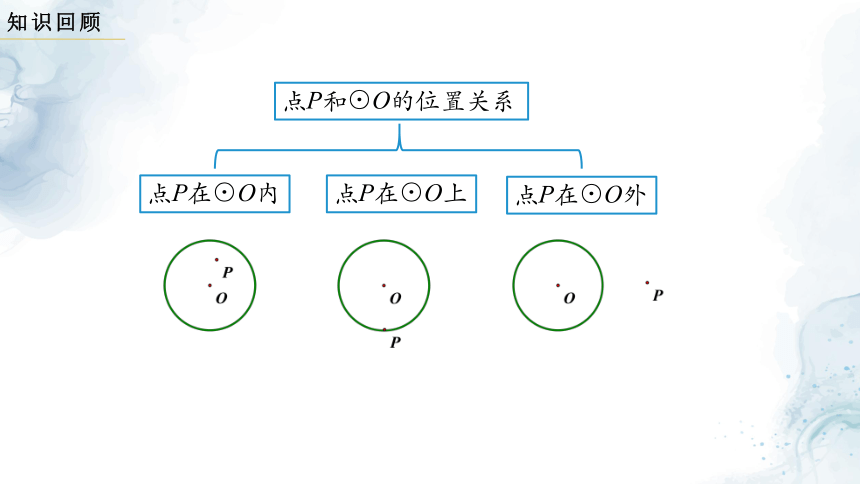
点P和⊙O的位置关系
点P在⊙O内
点P在⊙O上
点P在⊙O外
知识回顾
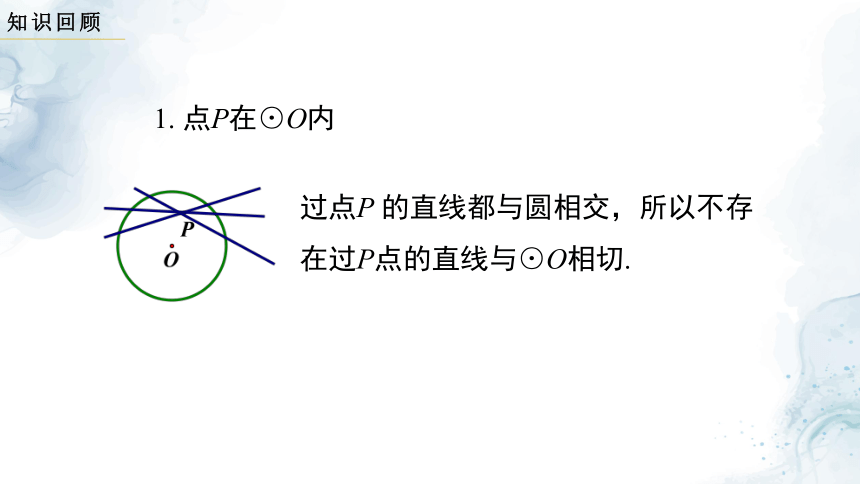
1. 点P在⊙O内
过点P 的直线都与圆相交,所以不存在过P点的直线与⊙O相切.
知识回顾
2. 点P在⊙O上
作法:
①连接OP;
②过P点作已知线段OP的垂线l,
直线l即为⊙O的切线.
作图依据:经过半径的外端并且垂直于这条半径的直线是圆的切线.
知识回顾
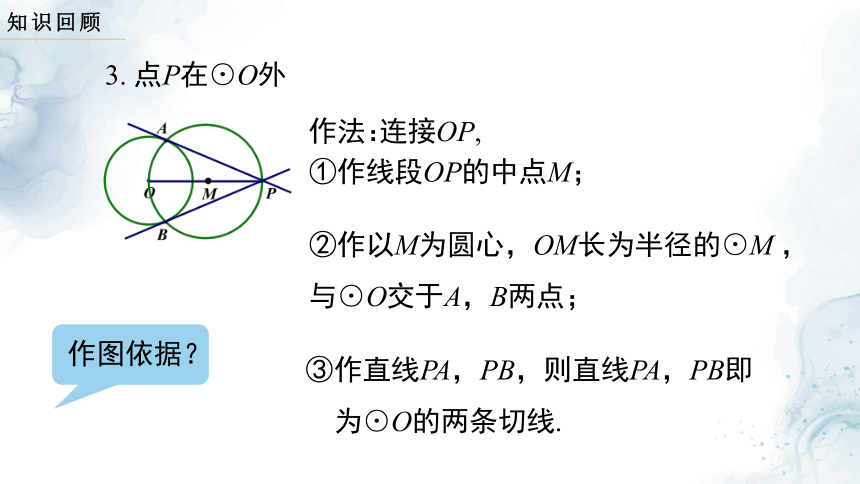
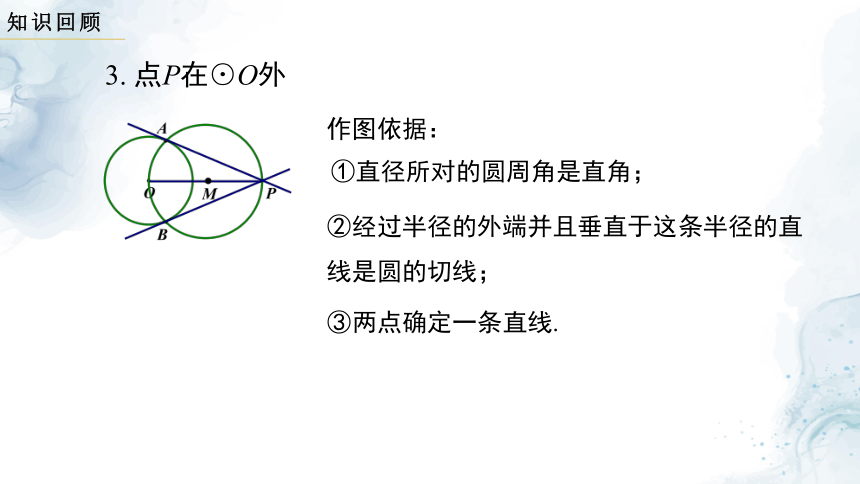
3. 点P在⊙O外
作法:
连接OP,
①作线段OP的中点M;
②作以M为圆心,OM长为半径的⊙M ,与⊙O交于A,B两点;
③作直线PA,PB,则直线PA,PB即
为⊙O的两条切线.
作图依据?
知识回顾
3. 点P在⊙O外
作图依据:
①直径所对的圆周角是直角;
②经过半径的外端并且垂直于这条半径的直线是圆的切线;
③两点确定一条直线.
知识回顾
总结:
点P在⊙O内,过P点,不存在圆的切线;
点P在⊙O上,过P点,可以作圆的一条切线;
点P在⊙O外,过P点,可以作圆的两条切线.
探索新知 知识点1 切线长定理及其应用
A
P
O
B
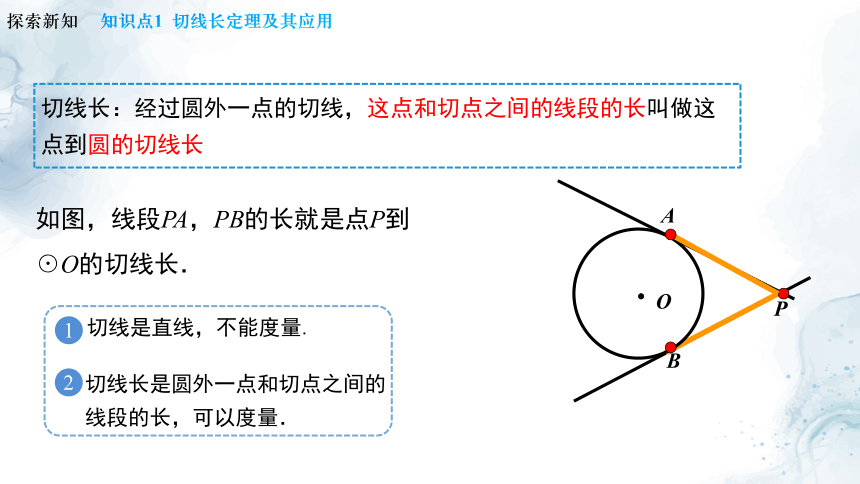
如图,线段PA,PB的长就是点P到☉O的切线长.
切线长:经过圆外一点的切线,这点和切点之间的线段的长叫做这点到圆的切线长
切线是直线,不能度量.
切线长是圆外一点和切点之间的线段的长,可以度量.
1
2
探索新知 知识点1 切线长定理及其应用
探究
如图,PA,PB是☉O的两条切线,切点分别为A,B. 在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
PA=PB
∠APO=∠BPO
你能证明你的结论吗?
猜想:
探索新知 知识点1 切线长定理及其应用
探究
如图,PA,PB是☉O的两条切线,切点分别为A,B. 在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
证明:连接OA,OB
∵PA和PB是☉O 的两条切线,
∴OA⊥AP,OB⊥BP.
又OA=OB,OP=OP,
∴Rt△AOP≌ Rt△BOP.
∴PA=PB,∠APO=∠BPO
∟
∟
思考
你能用简洁的语言把这一结论总结出来吗?
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角.
符号表示:
∵PA、PB分别与☉O相切于点A、B,
∴ PA = PB ,
∠OPA=∠OPB.
探索新知 知识点1 切线长定理及其应用
思考
若连接两切点 A,B,AB 交 OP 于点 M. 你又能得出什么新的结论 请给出证明.
探索新知 知识点1 切线长定理及其应用
解:OP 垂直平分 AB.
证明:∵ PA,PB 是 ☉O 的切线,
点 A,B 是切点,
∴ PA = PB,∠OPA =∠OPB.
∴ △PAB 是等腰三角形,
PM 为顶角的平分线.
∴ OP 垂直平分 AB.
M
O
P
A
B
PA、PB是☉O的两条切线,A、B为切点,直线OP交☉O于点D、E,交AB于C.
探索新知 知识点1 切线长定理及其应用
延伸
B
P
O
A
C
E
D
(1)图中所有的垂直关系:OA⊥PA,OB ⊥PB,AB ⊥OP.
(2)图中与∠OAC和∠AOC相等的角:
∠OAC=∠OBC=∠APC=∠BPC.
∠AOC=∠BOC=∠PAC=∠PBC
(3)图中所有的相等的线段:
PA=PB,AC =BC,OA =OB.
(4)图中所有的全等三角形:
△AOP≌ △BOP,
△AOC≌ △BOC,
△ACP≌ △BCP.
(5)图中所有的等腰三角形:
△ABP ,△AOB
探索新知 知识点2 三角形的内切圆及其作法
思考
如图,下面是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三条边都相切?请动手画一画.
作圆的关键是什么?
确定圆心和半径.
怎样确定圆心的位置?
作两条角平分线,其交点就是圆心的位置.
圆心的位置确定后,怎样确定圆的半径?
过圆心作三角形一边的垂线,垂线段的长
就是圆的半径.
圆心到三条边的距离相等
角平分线上的点到角的两边的距离相等
相切时圆心到直线的距离等于半径
探索新知 知识点2 三角形的内切圆及其作法
已知△ABC,求作一个圆,使它与△ABC的三条边都相切.
I
M
N
∟
D
作法:
1.作∠ABC、∠ACB的平分线BM和CN,交点为I;
2.过点I作ID⊥BC,垂足为D;
3.以I为圆心,ID为半径作☉I,☉I就是所求.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
与三角形各边都相切的圆叫做三角形的内切圆.
三角形的内切圆
三角形的内心
三角形内心的性质
三角形的内心是三角形三条角平分线的交点.
三角形的内心到三角形三边的距离相等.
B
A
C
I
E
F
G
AI、BI、CI 分别平分∠CAB、∠ABC、∠BCA,IE=IF=IG.
探索新知 知识点2 三角形的内切圆及其作法
例2 △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13,求AF、BD、CE的长.
根据切线长定理可以得到:AF=AE,BF=BD,CD=CE.如果设AF=x,那么其他线段就都可以用含x的式子来表示,然后利用线段之间的和差关系建立方程即可求出.
分析:
A
C
E
D
F
O
B
例2 △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13,求AF、BD、CE的长.
解:设AF=x,则AE=x,
CD=CE=AC AE=13 x,
BD=BF=AB AF=9 x.
由BD+CD=BC,可得
(9 x)+(13 x)=14.
解得x=4.
因此AF=4,BD=5,CE=9.
A
C
E
D
F
O
B
x
x
13 x
13 x
9 x
9 x
14
方程思想
有关三角形内切圆的两个重要结论
延伸
探索新知 知识点2 三角形的内切圆及其作法
若已知△ABC的面积为 ,求△ABC内切圆的半径.
解:
有关三角形内切圆的两个重要结论
延伸
探索新知 知识点2 三角形的内切圆及其作法
其中a,b为直角三角形的直角边长;c为斜边长.
探索新知 知识点2 三角形的内切圆及其作法
三角形的外接圆与三角形的内切圆,有什么区别呢?
图形 名称 性质 位置 角度关系
外心:三角形外接圆的圆心(或三角形三边中垂线的交点).
三角形外心到三角形的三个顶点的距离相等.即OA=OB=OC.
锐角三角形的外心在形内;
直角三角形的外心在斜边中点;
钝角三角形的外心在形外.
内心:三角形内切圆的圆心(或三角形三内角平分线的交点).
三角形内心到三角形的三边的距离相等.即ID=IE=IF.
三角形的内心一定在三角形内.
当堂检测
Part Three
叁
D
B
B
C
A
课堂总结
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
有关概念
内心概念及性质
应用
THANKS
感谢观看
Enter The Appropriate Content Here, Or After Copying The Text
演讲人:
20XX
24.2.2直线和圆的位置关系(第3课时)
人教版(2012)九年级上册
学习目录
Part One
壹
学习目录
了解切线长的定义及切线长定理
1
会运用切线长定理进行计算与证明
2
认识三角形的内切圆及其有关概念,会作一个三角形的内切圆,掌握内心的性质
3
探索新知
Part Two
贰
知识回顾
还记得上节课我们学习的过圆上一点作已知圆的切线吗?
∟
o
P
l
在同一个平面内,有一点P和☉O,过点P能否作☉O的切线?如果能,可以作几条切线?如果不能,说明理由.
知识回顾
点P和⊙O的位置关系
点P在⊙O内
点P在⊙O上
点P在⊙O外
知识回顾
1. 点P在⊙O内
过点P 的直线都与圆相交,所以不存在过P点的直线与⊙O相切.
知识回顾
2. 点P在⊙O上
作法:
①连接OP;
②过P点作已知线段OP的垂线l,
直线l即为⊙O的切线.
作图依据:经过半径的外端并且垂直于这条半径的直线是圆的切线.
知识回顾
3. 点P在⊙O外
作法:
连接OP,
①作线段OP的中点M;
②作以M为圆心,OM长为半径的⊙M ,与⊙O交于A,B两点;
③作直线PA,PB,则直线PA,PB即
为⊙O的两条切线.
作图依据?
知识回顾
3. 点P在⊙O外
作图依据:
①直径所对的圆周角是直角;
②经过半径的外端并且垂直于这条半径的直线是圆的切线;
③两点确定一条直线.
知识回顾
总结:
点P在⊙O内,过P点,不存在圆的切线;
点P在⊙O上,过P点,可以作圆的一条切线;
点P在⊙O外,过P点,可以作圆的两条切线.
探索新知 知识点1 切线长定理及其应用
A
P
O
B
如图,线段PA,PB的长就是点P到☉O的切线长.
切线长:经过圆外一点的切线,这点和切点之间的线段的长叫做这点到圆的切线长
切线是直线,不能度量.
切线长是圆外一点和切点之间的线段的长,可以度量.
1
2
探索新知 知识点1 切线长定理及其应用
探究
如图,PA,PB是☉O的两条切线,切点分别为A,B. 在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
PA=PB
∠APO=∠BPO
你能证明你的结论吗?
猜想:
探索新知 知识点1 切线长定理及其应用
探究
如图,PA,PB是☉O的两条切线,切点分别为A,B. 在半透明的纸上画出这个图形,沿着直线PO将图形对折,图中的PA与PB,∠APO与∠BPO有什么关系?
证明:连接OA,OB
∵PA和PB是☉O 的两条切线,
∴OA⊥AP,OB⊥BP.
又OA=OB,OP=OP,
∴Rt△AOP≌ Rt△BOP.
∴PA=PB,∠APO=∠BPO
∟
∟
思考
你能用简洁的语言把这一结论总结出来吗?
切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角.
符号表示:
∵PA、PB分别与☉O相切于点A、B,
∴ PA = PB ,
∠OPA=∠OPB.
探索新知 知识点1 切线长定理及其应用
思考
若连接两切点 A,B,AB 交 OP 于点 M. 你又能得出什么新的结论 请给出证明.
探索新知 知识点1 切线长定理及其应用
解:OP 垂直平分 AB.
证明:∵ PA,PB 是 ☉O 的切线,
点 A,B 是切点,
∴ PA = PB,∠OPA =∠OPB.
∴ △PAB 是等腰三角形,
PM 为顶角的平分线.
∴ OP 垂直平分 AB.
M
O
P
A
B
PA、PB是☉O的两条切线,A、B为切点,直线OP交☉O于点D、E,交AB于C.
探索新知 知识点1 切线长定理及其应用
延伸
B
P
O
A
C
E
D
(1)图中所有的垂直关系:OA⊥PA,OB ⊥PB,AB ⊥OP.
(2)图中与∠OAC和∠AOC相等的角:
∠OAC=∠OBC=∠APC=∠BPC.
∠AOC=∠BOC=∠PAC=∠PBC
(3)图中所有的相等的线段:
PA=PB,AC =BC,OA =OB.
(4)图中所有的全等三角形:
△AOP≌ △BOP,
△AOC≌ △BOC,
△ACP≌ △BCP.
(5)图中所有的等腰三角形:
△ABP ,△AOB
探索新知 知识点2 三角形的内切圆及其作法
思考
如图,下面是一块三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下来的圆与三角形的三条边都相切?请动手画一画.
作圆的关键是什么?
确定圆心和半径.
怎样确定圆心的位置?
作两条角平分线,其交点就是圆心的位置.
圆心的位置确定后,怎样确定圆的半径?
过圆心作三角形一边的垂线,垂线段的长
就是圆的半径.
圆心到三条边的距离相等
角平分线上的点到角的两边的距离相等
相切时圆心到直线的距离等于半径
探索新知 知识点2 三角形的内切圆及其作法
已知△ABC,求作一个圆,使它与△ABC的三条边都相切.
I
M
N
∟
D
作法:
1.作∠ABC、∠ACB的平分线BM和CN,交点为I;
2.过点I作ID⊥BC,垂足为D;
3.以I为圆心,ID为半径作☉I,☉I就是所求.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
与三角形各边都相切的圆叫做三角形的内切圆.
三角形的内切圆
三角形的内心
三角形内心的性质
三角形的内心是三角形三条角平分线的交点.
三角形的内心到三角形三边的距离相等.
B
A
C
I
E
F
G
AI、BI、CI 分别平分∠CAB、∠ABC、∠BCA,IE=IF=IG.
探索新知 知识点2 三角形的内切圆及其作法
例2 △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13,求AF、BD、CE的长.
根据切线长定理可以得到:AF=AE,BF=BD,CD=CE.如果设AF=x,那么其他线段就都可以用含x的式子来表示,然后利用线段之间的和差关系建立方程即可求出.
分析:
A
C
E
D
F
O
B
例2 △ABC的内切圆☉O与BC、CA、AB分别相切于点D、E、F,且AB=9,BC=14,CA=13,求AF、BD、CE的长.
解:设AF=x,则AE=x,
CD=CE=AC AE=13 x,
BD=BF=AB AF=9 x.
由BD+CD=BC,可得
(9 x)+(13 x)=14.
解得x=4.
因此AF=4,BD=5,CE=9.
A
C
E
D
F
O
B
x
x
13 x
13 x
9 x
9 x
14
方程思想
有关三角形内切圆的两个重要结论
延伸
探索新知 知识点2 三角形的内切圆及其作法
若已知△ABC的面积为 ,求△ABC内切圆的半径.
解:
有关三角形内切圆的两个重要结论
延伸
探索新知 知识点2 三角形的内切圆及其作法
其中a,b为直角三角形的直角边长;c为斜边长.
探索新知 知识点2 三角形的内切圆及其作法
三角形的外接圆与三角形的内切圆,有什么区别呢?
图形 名称 性质 位置 角度关系
外心:三角形外接圆的圆心(或三角形三边中垂线的交点).
三角形外心到三角形的三个顶点的距离相等.即OA=OB=OC.
锐角三角形的外心在形内;
直角三角形的外心在斜边中点;
钝角三角形的外心在形外.
内心:三角形内切圆的圆心(或三角形三内角平分线的交点).
三角形内心到三角形的三边的距离相等.即ID=IE=IF.
三角形的内心一定在三角形内.
当堂检测
Part Three
叁
D
B
B
C
A
课堂总结
切线长
切线长定理
作用
图形的轴对称性
原理
提供了证线段和
角相等的新方法
辅助线
分别连接圆心和切点;
连接两切点;
连接圆心和圆外一点.
三角形内切圆
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
有关概念
内心概念及性质
应用
THANKS
感谢观看
Enter The Appropriate Content Here, Or After Copying The Text
演讲人:
20XX
同课章节目录
