2024-2025学年度第一学期期中质量检测高二数学试题(含解析)
文档属性
| 名称 | 2024-2025学年度第一学期期中质量检测高二数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 594.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 10:18:36 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年度第一学期期中质量检测
高二数学试题(含解析)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.本试卷共19小题,满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2AB铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷 (选择题 共58分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知平面的法向量为(2,-2,4),=(-1,1,-2),则直线AB与平面α的位置关系为( )
A.AB α B.AB α C.AB与α相交但不垂直 D.AB∥α
2.直线的倾斜角为( )
A. 75° B.105° C.15° D.60°
3.“a=±4”是“圆x2+y2=1与圆x2+(y+a)2=9相切”的( )
A.充分不必要条件 B.必要不充分条件 C. 既不充分也不必要条件 D.充要条件
4.在空间直角坐标系中,已知A(1,0,1),B(1,1,1),C(0,0,),则点A到直线BC的距离为( )
A. 3 B. 5 C. D.
5.与直线3x-4y+5=0关于x轴对称的直线的方程是( )
A.3x-4y+5=0 B.3x-4y-5=0 C.3x+4y+5=0 D.3x+4y-5=0
6.某广场一个椭球水景雕塑如图所示,其横截面为圆,过横截面圆心的纵截面为椭圆,
该椭圆的离心率为.若该椭球的横截面的最大直径为1.8m,则该椭球的高为( )
A.3.2m B.3.4m
C.4m D.3.6m
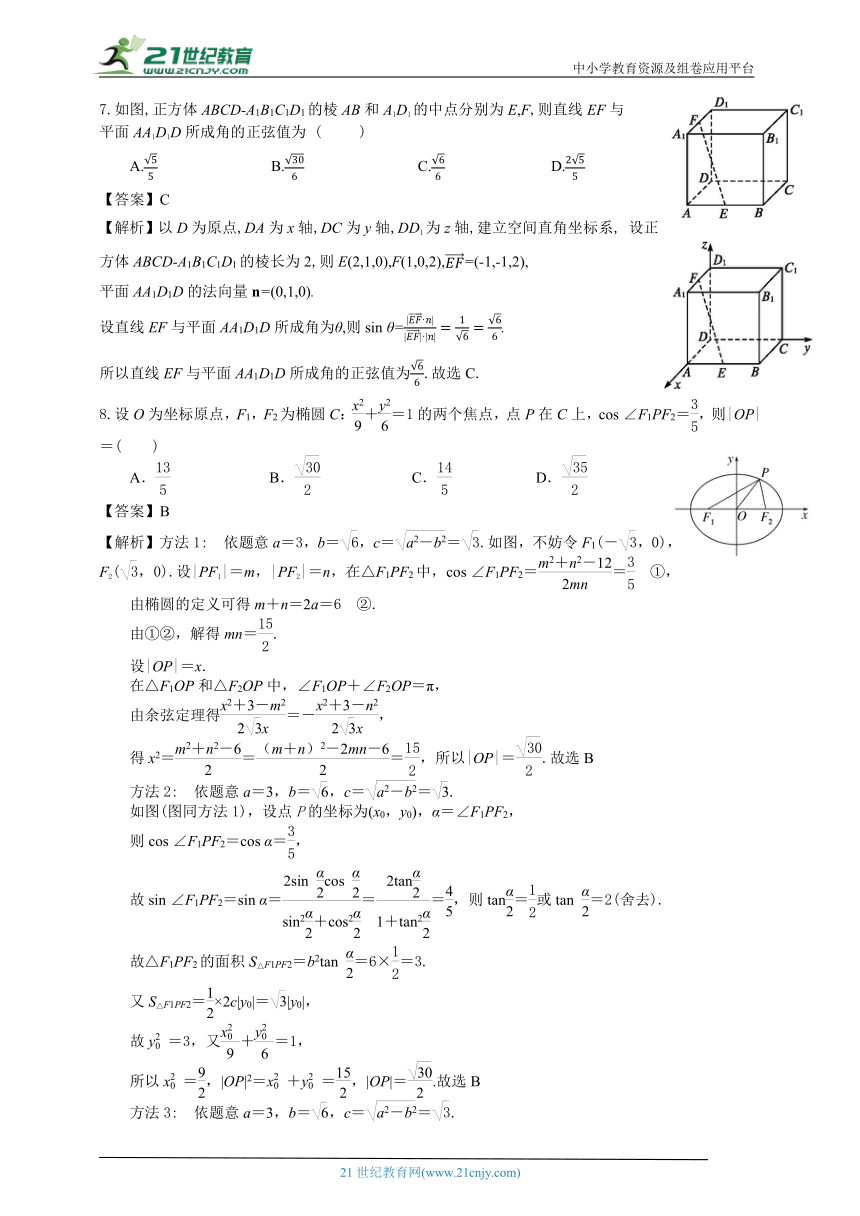
7.如图,正方体ABCD-A1B1C1D1的棱AB和A1D1的中点分别为E,F,则直线EF与
平面AA1D1D所成角的正弦值为 ( )
A. B. C. D.
8.设O为坐标原点,F1,F2为椭圆C:+=1的两个焦点,点P在C上,cos ∠F1PF2=,则|OP|=( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.已知点P是平行四边形ABCD所在的平面外一点,如果=(2,-1,-4),=(4,2,0),=(-1,2,-1).则下列结论正确的是( )
A. AP AB B.AP AD C. 是平面ABCD的法向量 D. ∥
10.已知直线l:(1-2m)x-(m-1)y+7m-4=0, 圆C:x2+y2-2x-4y-20=0,则以下命题正确的是( )
A.直线l恒过定点(-3,-1) B.直线l与圆C恒相交
C.圆C被x轴截得的弦长为 D.直线l被圆C截得的弦最短时,
11.已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线与椭圆C交于A,B两点,且|AB|=3,则( )
A.椭圆的焦点在y轴上 B.△ABF1的周长为6
C.△AF1F2的周长为6 D.椭圆C的方程为=1
第Ⅱ卷 (非选择题 共92分)
填空题:本题共3小题,每小题5分,共15分.
12.圆x2+y2=8内有一点P(2,-1),AB为过点P的弦,则AB的中点Q的轨迹方程为 .
13.已知F1,F2为椭圆C:+=1的两个焦点,P,Q为C上关于坐标原点对称的两点,且|PQ|=|F1F2|,则四边形PF1QF2的面积为________.
14.在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体,
该几何体的上、下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分).
现有一个如图所示的曲池,它的高为2,AA1,BB1,CC1,DD1均与曲池的底面
垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为90°,则图
中异面直线AB1与CD1所成角的余弦值为 .
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分13分)
已知△ABC的顶点C(2,-8),直线AB的方程为y=-2x+11,AC边上的高BH所在直线的方程为x+3y+2=0.
⑴求顶点A和B的坐标;
⑵求△ABC外接圆的一般方程.
16.(本题满分15分)
如图,已知四棱锥P-ABCD的底面ABCD是矩形,PA 平面ABCD,
PA=AD=2,BD=.
⑴求证:BD 平面PAC;
⑵求二面角P-CD-B的余弦值的大小;
⑶求点C到平面PBD的距离.
17.(本题满分15分)
已知动点P与平面上点A(-1,0),B(1,0)的距离之和等于2.
⑴试求动点P的轨迹方程C;
⑵设直线l: 与曲线C交于M、N两点,当|MN|=时,求直线l的方程.
18.(本题满分17分)
如图1,等腰梯形AECD是由三个全等的等边三角形拼成,现△BCE将沿BC翻折至△BCP,使得PD=AB,如图2所示.
⑴求证:PD BC;
⑵在直线PD上是否存在点M,使得直线BM与平面APD所成角的余弦值为 ?若存在,求出的值; 若不存在,说明理由.
19.(本题满分17分)
如图,在平面直角坐标系xOy中,已知椭圆C:(a>b>0)的离心率e=,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
⑴求椭圆C的方程;
⑵已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP EQ,若存在,求出点Q的坐标;若不存在说明理由;
⑶若过O点作直线l的平行线交椭圆C于点M,求的最小值.
试题解析
选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知平面的法向量为(2,-2,4),=(-1,1,-2),则直线AB与平面α的位置关系为( )
A.AB α B.AB α C.AB与α相交但不垂直 D.AB∥α
【答案】A
【解析】∵(2,-2,4),=(-1,1,-2),,∴,∴∥,∴AB α.故选A.
2.直线的倾斜角为( )
A. 75° B.105° C.15° D.60°
【答案】B
【解析】由题意得,直线的斜率, 则直线的倾斜角为105°.故选B.
3.“a=±4”是“圆x2+y2=1与圆x2+(y+a)2=9相切”的( )
A.充分不必要条件 B.必要不充分条件 C. 既不充分也不必要条件 D.充要条件
【答案】A
【解析】若a=±4,则圆x2+y2=1与圆x2+(y+a)2=9相外切;若圆x2+y2=1与圆x2+(y+a)2=9相切,分外切和内切,a不一定等于±4,也可能等于2或-2.所以“a=±4”是“圆x2+y2=1与圆x2+(y+a)2=9相切”的充分不必要条件.故选A.
4.在空间直角坐标系中,已知A(1,0,1),B(1,1,1),C(0,0,),则点A到直线BC的距离为( )
A. 3 B. 5 C. D.
【答案】D
【解析】∵=(0,1,0),,=(-1,-1,),直线BC的方向向量,则点A到直线BC的距离为,故选D.
5.与直线3x-4y+5=0关于x轴对称的直线的方程是( )
A.3x-4y+5=0 B.3x-4y-5=0 C.3x+4y+5=0 D.3x+4y-5=0
【答案】C
【解析】设所求直线上点的坐标(x,y),则关于x轴的对称点的坐标(x,-y)在已知的直线3x-4y+5=0上,∴所求对称直线方程为3x+4y+5=0. 故选C.
6.某广场一个椭球水景雕塑如图所示,其横截面为圆,过横截面圆心的纵截面为椭圆,该椭圆的离心率为.若该椭球的横截面的最大直径为1.8m,则该椭球的高为( )
A.3.2m B.3.4m
C.4m D.3.6m
【答案】D.
【解析】由题意知,e=,∴a=2b,由该椭球的横截面的最大直径为1.8m,可知2b=1.8m,即a=1.8m,该椭球的高2a=3.6m.故选D.
7.如图,正方体ABCD-A1B1C1D1的棱AB和A1D1的中点分别为E,F,则直线EF与
平面AA1D1D所成角的正弦值为 ( )
A. B. C. D.
【答案】C
【解析】以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系, 设正方体ABCD-A1B1C1D1的棱长为2,则E(2,1,0),F(1,0,2),=(-1,-1,2),
平面AA1D1D的法向量n=(0,1,0).
设直线EF与平面AA1D1D所成角为θ,则sin θ=.
所以直线EF与平面AA1D1D所成角的正弦值为.故选C.
8.设O为坐标原点,F1,F2为椭圆C:+=1的两个焦点,点P在C上,cos ∠F1PF2=,则|OP|=( )
A. B. C. D.
【答案】B
【解析】方法1: 依题意a=3,b=,c==.如图,不妨令F1(-,0),F2(,0).设|PF1|=m,|PF2|=n,在△F1PF2中,cos ∠F1PF2== ①,
由椭圆的定义可得m+n=2a=6 ②.
由①②,解得mn=.
设|OP|=x.
在△F1OP和△F2OP中,∠F1OP+∠F2OP=π,
由余弦定理得=-,
得x2===,所以|OP|=.故选B
方法2: 依题意a=3,b=,c==.
如图(图同方法1),设点P的坐标为(x0,y0),α=∠F1PF2,
则cos ∠F1PF2=cos α=,
故sin ∠F1PF2=sin α===,则tan=或tan =2(舍去).
故△F1PF2的面积S△F1PF2=b2tan =6×=3.
又S△F1PF2=×2c|y0|=|y0|,
故y=3,又+=1,
所以x=,|OP|2=x+y=,|OP|=.故选B
方法3: 依题意a=3,b=,c==.
如图(图同方法1),设点P的坐标为(x0,y0),利用焦点三角形面积公式知S△F1PF2=.
因为cos ∠F1PF2=,所以sin ∠F1PF2=,故S△F1PF2==3.又S△F1PF2=×2c|y0|=|y0|,
故y=3,
又+=1,所以x=,|OP|2=x+y=,|OP|=.故选B
方法4: 依题意a=3,b=,c==.
如图(图同方法1),不妨令F1(-,0),F2(,0).
设|PF1|=m,|PF2|=n,在△F1PF2中,cos ∠F1PF2== ①,
由椭圆的定义可得m+n=2a=6 ②.
由①②,解得mn=.
因为=(+),
所以||2=(m2+n2+2mn cos ∠F1PF2)==,所以|PO|=.故选B.
选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.已知点P是平行四边形ABCD所在的平面外一点,如果=(2,-1,-4),=(4,2,0),=(-1,2,-1).则下列结论正确的是( )
A. AP AB B.AP AD C. 是平面ABCD的法向量 D. ∥
【答案】ABC
【解析】∵=0,=0, ∴AP AB,AP AD,即选项A,B正确;
又与不平行, ∴是平面ABCD的法向量,选项C正确 ;
∵=(2,3,4),=(-1,2,-1),∴与 不平行,选项D错误.
故选ABC.
10.已知直线l:(1-2m)x-(m-1)y+7m-4=0, 圆C:x2+y2-2x-4y-20=0,则以下命题正确 的是( )
A.直线l恒过定点(-3,-1) B.直线l与圆C恒相交
C.圆C被x轴截得的弦长为 D.直线l被圆C截得的弦最短时,
【答案】BC
【解析】依题意,直线l:(1-2m)x-(m-1)y+7m-4=0可化为(-2x-y+7)m+x+y-4=0,
由解得x=3,y=1,即直线l恒过定点P(3,1),选项A错误;
∵圆方程x2+y2-2x-4y-20=0可化为(x-1)2+(y-2)2=25,∴圆C的圆心为C(1,2),半径为r=5,
|PC|=圆心C到x轴的距离d=2,则圆C被x轴截得的弦长为2,选项C正确;
由于直线l过定点P(3,1),而,∴当直线l被圆C截得的弦最短时,l PC,
=2,即,,则选项D错误.
故选BC.
11.已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线与椭圆C交于A,B两点,且|AB|=3,则( )
A.椭圆的焦点在y轴上 B.△ABF1的周长为6
C.△AF1F2的周长为6 D.椭圆C的方程为=1
【答案】CD
【解析】显然椭圆的焦点在x轴上,A错误.
设椭圆C的方程为=1(a>b>0),c=1.
∵过F2且垂直于x轴的直线与椭圆交于A,B两点,设A(c,y1),
代入方程可得+=1.求得.由于|AB|=3,
∴=,b2=a2-c2,所以a2=4,a=2,b2=a2-c2=4-1=3,
椭圆的方程为=1,△ABF1的周长为4a=8,△AF1F2的周长为2a+2c=6.
故选CD.
填空题:本题共3小题,每小题5分,共15分.
12.圆x2+y2=8内有一点P(2,-1),AB为过点P的弦,则AB的中点Q的轨迹方程为 .
【答案】x2+y2+y-2x=0
【解析】设AB的中点为Q(x,y),则AB的斜率为k=,又OQ⊥AB,
∴kOQ·k=-1,即,整理得x2+y2+y-2x=0,
∴过点P的弦中点的轨迹方程为x2+y2+y-2x=0.
13.已知F1,F2为椭圆C:+=1的两个焦点,P,Q为C上关于坐标原点对称的两点,且|PQ|=|F1F2|,则四边形PF1QF2的面积为________.
【答案】8.
【解析】根据椭圆的对称性及|PQ|=|F1F2|可以得到四边形PF1QF2为对角线相等的平行四边形,所以四边形PF1QF2为矩形.设|PF1|=m,则|PF2|=2a-|PF1|=8-m,则|PF1|2+|PF2|2=m2+(8-m)2=2m2+64-16m=|F1F2|2=4c2=4(a2-b2)=48,得m(8-m)=8,所以四边形PF1QF2的面积为|PF1|×|PF2|=m(8-m)=8.
14.在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体,
该几何体的上、下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分).
现有一个如图所示的曲池,它的高为2,AA1,BB1,CC1,DD1均与曲池的底面
垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为90°,则图中异面直线AB1与CD1所成角的余弦值为 .
【答案】
【解析】设上底面圆心为O,下底面圆心为O′,连接OO′,OB,OC,以O为原点,分
别以OC,OB,OO′ 所在直线为x轴,y轴,z轴建立空间直角坐标系,则C(1,0,0),
A(0,2,0),B1(0,1,2),D1(2,0,2),
∴=(0,-1,2),=(1,0,2),
∴.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.已知△ABC的顶点C(2,-8),直线AB的方程为y=-2x+11,AC边上的高BH所在直线的方程为x+3y+2=0.
⑴求顶点A和B的坐标;
⑵求△ABC外接圆的一般方程.
【答案】⑴A(5,1),B(7,-3); ⑵x2+y2.
【解析】⑴联立,解得,
∴顶点B(7,-3),
∵AC⊥BH,∴kAC·kBH=-1,
已知kBH=-,∴kAC=3,
∴设直线AC的方程为y=3x+b,
将C(2,-8)代入得b=-14,
∴直线AC的方程为y=3x-14.
由,可得顶点A(5,1).
⑵设△ABC的外接圆方程为x2+y2+Dx+Ey+F=0,
将A(5,1),B(7,-3)和C(2,-8)三点的坐标分别代入,得
,解得D=-4,E=6,F=-12,
∴x2+y2
16.如图,已知四棱锥P-ABCD的底面ABCD是矩形,PA 平面ABCD,
PA=AD=2,BD=.
⑴求证:BD 平面PAC;
⑵求二面角P-CD-B的余弦值的大小;
⑶求点C到平面PBD的距离.
【答案】⑴详见解析; ⑵; ⑶
【解析】⑴证明:∵四棱锥P-ABCD的底面ABCD是矩形,PA 平面ABCD,PA=AD=2,BD=.
∴PA BD,AB==2,
∴四边形ABCD为正方形,
∴BD AC,
又AC,PA 平面PAC,AC∩PA=A,
∴BD 平面PAC
⑵方法1:∵四棱锥P-ABCD的底面ABCD是矩形,PA 平面ABCD,PA=AD=2,BD=.
∴PA CD,AD CD,
∴CD 平面PAD,
∴CD PD,
∴∠PDA是二面角P-CD-B的的平面角,
∵PA=AD=2,PA AD,
∴∠PDA=45°,cos∠PDA=cos45°=
∴二面角P-CD-B的余弦值为.
方法2:如图,以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,则C(2,2,0),D(0,2,0),P(0,0,2),
=(2,2,-2),=(0,2,-2),
设平面PCD的法向量=(x,y,z),则
,即,
取y=z=1,x=0,则=(0,1,1),
显然,平面ABCD的法向量=(0,0,1),
设二面角P-CD-B的平面角为θ,则
,
∴二面角P-CD-B的余弦值为.
⑶同⑵方法2建立空间直角坐标系,则
=(2,0,-2),=(2,2,-2),=(0,2,-2),
设平面PBD的法向量=(x0,y0,z0),则
,即,
取x0=y0=z0=1,则=(1,1,1),
∴点C到平面PBD的距离.
17.已知动点P与平面上点A(-1,0),B(1,0)的距离之和等于2.
⑴试求动点P的轨迹方程C;
⑵设直线l: 与曲线C交于M、N两点,当|MN|=时,求直线l的方程.
【答案】⑴;⑵y=x-.
【解析】⑴设动点P的坐标为(x,y),
∵|PA|+|PB|=2>2=|AB|,
∴由椭圆定义可知点P轨迹是以A,B为焦点的椭圆.
∴a=,c=1,b==1,
∴动点P的轨迹方程C为:.
⑵将直线l: 代入椭圆方程得:(1+2k2)x2-4kx+4=0,
∴ =,即k2>1,
设M(x1,y1),N(x2,y2),
∴x1+x2=, ,
∴|MN|=
=.
∴17k4-32k2-57=0,即(17k2+19)(k2-3)=0,
∴k2=3,.
∴直线l的方程为y=x-.
18.如图1,等腰梯形AECD是由三个全等的等边三角形拼成,现△BCE将沿BC翻折至△BCP,使得PD=AB,如图2所示.
⑴求证:PD BC;
⑵在直线PD上是否存在点M,使得直线BM与平面APD所成角的余弦值为 ?若存在,求出的值; 若不存在,说明理由.
【答案】⑴详见解析; ⑵在直线PD上存在点M,使得直线BM与平面APD所成角的余弦值为.此时,的值为2或.
【解析】⑴证明:在图1连接DE交BC于O点,
在图2中,易知△BCD、△BCP 都是等边三角形,
易得DO BC,PO BC,
又DO,PO 平面POD,DO∩PO=O,
∴BC 平面POD,
∴PD BC.
⑵方法1:假设存在点M,符合题意.
设AB=2,则PD=3,
则在△POD中,由OD=OP=,PD=3,由余弦定理得∠POD=120°,
由⑴得BC 平面POD,
又AD∥BC,∴直线AD 平面POD,
∵AD 平面ADP,∴平面ADP 平面POD,
作OQ PD,垂足为Q,则OQ 平面ADP,
在△POD中,由OD=OP=,PD=3,∠POD=120°,
∴OQ=.
如图3,取AP的中点N,连接BN,QN,
由QN∥AD,OB∥AD,得QN∥OB,
又QN=AD=OB,
∴四边形BNQO为平行四边形,
∵OQ 平面ADP,∴BN 平面ADP,
则直线BM与平面APD所成角θ为∠BMN,且BN=OQ=.
由已知得,得,
由BN=BMsin∠BMN=,得BM=,
在△BDM 中,设DM=t,由余弦定理得
,即t2-3t+2=0,
解得t=1或t=2,
∴在直线PD上存在点M,使得直线BM与平面APD所成角的余弦值为.此时,的值为2或.
方法2(等体积法):设AB=2,则PD=3,
则在△POD中,由OD=OP=,PD=3,由余弦定理得∠POD=120°,
作PH DO,垂足为H,连OH,得∠POH=60°,
∴PH=POsin60°=.
由⑴得BC 平面POD,
又AD∥BC,∴直线AD 平面POD,
∴AD PD,即△ADP为直角三角形,
∴△ADP的面积为×AD×PD=×2×3=3,
设点B到平面ADP的距离为h,由VP-ABD=VB-ADP,得
,得h=.
设直线BM与平面APD所成角为θ,则,∴,
∴h=BMsinθ=,得BM=,
在△BDM 中,设DM=t,由余弦定理得
,即t2-3t+2=0,
解得t=1或t=2,
∴在直线PD上存在点M,使得直线BM与平面APD所成角的余弦值为.此时,的值为2或.
方法3(向量法):由方法2知PH=,如图3,以BC的中点O为原点,OB,DO,OZ分别为x,y,z 轴的正方向,建立空间直角坐标系.则B(1,0,0),A(2,,0),D(0,,0),P(0,,).
∴,,
设平面APD的法向量=(x,y,z),则
,即,
解得x=0,令y=-1,得z=,
即=(0,-1,).
设存在点M,,满足题意.
则,
∴,
设直线BM与平面APD所成角为θ,则,∴,
∴.
解得,
∴在直线PD上存在点M,使得直线BM与平面APD所成角的余弦值为.此时,的值为2或.
19.如图,在平面直角坐标系xOy中,已知椭圆C:(a>b>0)的离心率e=,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
⑴求椭圆C的方程;
⑵已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP EQ,若存在,求出点Q的坐标;若不存在说明理由;
⑶若过O点作直线l的平行线交椭圆C于点M,求的最小值.
【答案】⑴; ⑵存在定点Q,对于任意的k(k≠0)都有OP EQ,定点Q的坐标为(-3,0); ⑶当时,的最小值为.
【解析】⑴∵椭圆C:(a>b>0)的离心率e=,左顶点为A(-4,0),
∴a=4,c=2,b2=a2-c2=12.
∴椭圆C的方程为.
⑵直线l的方程为y=k(x+4),
由化简得(x+4)[(4k2+3)x+16k2-12]=0,
∴x1=-4,,
当x=时,,即点D(,),
∵点P为AD的中点,∴点P的坐标为(,),则(k≠0).
对直线l的方程为y=k(x+4),令x=0,得点E坐标为(0,4k),
假设存在定点Q(m,n)(m≠0),使得OP EQ,
则kOPkEQ=-1,即恒成立,
∴(4m+12)k-3n=0恒成立,
∴,即,
∴定点Q的坐标为(-3,0).
⑶∵OM∥l,∴OM的方程可设为y=kx,
由,得点M的横坐标为,
由OM∥l,得
,
当且仅当时,即时取等号,
∴当时,的最小值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年度第一学期期中质量检测
高二数学试题(含解析)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.本试卷共19小题,满分150分,考试时间120分钟.
注意事项:
1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.
2.选择题答案使用2AB铅笔填涂,如需改动,用橡皮擦干净后,再选涂其它答案标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,书写要工整、笔迹清楚,将答案书写在答题卡规定的位置上.
3.所有题目必须在答题卡上作答,在试卷上答题无效.
第Ⅰ卷 (选择题 共58分)
一.选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知平面的法向量为(2,-2,4),=(-1,1,-2),则直线AB与平面α的位置关系为( )
A.AB α B.AB α C.AB与α相交但不垂直 D.AB∥α
2.直线的倾斜角为( )
A. 75° B.105° C.15° D.60°
3.“a=±4”是“圆x2+y2=1与圆x2+(y+a)2=9相切”的( )
A.充分不必要条件 B.必要不充分条件 C. 既不充分也不必要条件 D.充要条件
4.在空间直角坐标系中,已知A(1,0,1),B(1,1,1),C(0,0,),则点A到直线BC的距离为( )
A. 3 B. 5 C. D.
5.与直线3x-4y+5=0关于x轴对称的直线的方程是( )
A.3x-4y+5=0 B.3x-4y-5=0 C.3x+4y+5=0 D.3x+4y-5=0
6.某广场一个椭球水景雕塑如图所示,其横截面为圆,过横截面圆心的纵截面为椭圆,
该椭圆的离心率为.若该椭球的横截面的最大直径为1.8m,则该椭球的高为( )
A.3.2m B.3.4m
C.4m D.3.6m
7.如图,正方体ABCD-A1B1C1D1的棱AB和A1D1的中点分别为E,F,则直线EF与
平面AA1D1D所成角的正弦值为 ( )
A. B. C. D.
8.设O为坐标原点,F1,F2为椭圆C:+=1的两个焦点,点P在C上,cos ∠F1PF2=,则|OP|=( )
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.已知点P是平行四边形ABCD所在的平面外一点,如果=(2,-1,-4),=(4,2,0),=(-1,2,-1).则下列结论正确的是( )
A. AP AB B.AP AD C. 是平面ABCD的法向量 D. ∥
10.已知直线l:(1-2m)x-(m-1)y+7m-4=0, 圆C:x2+y2-2x-4y-20=0,则以下命题正确的是( )
A.直线l恒过定点(-3,-1) B.直线l与圆C恒相交
C.圆C被x轴截得的弦长为 D.直线l被圆C截得的弦最短时,
11.已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线与椭圆C交于A,B两点,且|AB|=3,则( )
A.椭圆的焦点在y轴上 B.△ABF1的周长为6
C.△AF1F2的周长为6 D.椭圆C的方程为=1
第Ⅱ卷 (非选择题 共92分)
填空题:本题共3小题,每小题5分,共15分.
12.圆x2+y2=8内有一点P(2,-1),AB为过点P的弦,则AB的中点Q的轨迹方程为 .
13.已知F1,F2为椭圆C:+=1的两个焦点,P,Q为C上关于坐标原点对称的两点,且|PQ|=|F1F2|,则四边形PF1QF2的面积为________.
14.在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体,
该几何体的上、下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分).
现有一个如图所示的曲池,它的高为2,AA1,BB1,CC1,DD1均与曲池的底面
垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为90°,则图
中异面直线AB1与CD1所成角的余弦值为 .
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分13分)
已知△ABC的顶点C(2,-8),直线AB的方程为y=-2x+11,AC边上的高BH所在直线的方程为x+3y+2=0.
⑴求顶点A和B的坐标;
⑵求△ABC外接圆的一般方程.
16.(本题满分15分)
如图,已知四棱锥P-ABCD的底面ABCD是矩形,PA 平面ABCD,
PA=AD=2,BD=.
⑴求证:BD 平面PAC;
⑵求二面角P-CD-B的余弦值的大小;
⑶求点C到平面PBD的距离.
17.(本题满分15分)
已知动点P与平面上点A(-1,0),B(1,0)的距离之和等于2.
⑴试求动点P的轨迹方程C;
⑵设直线l: 与曲线C交于M、N两点,当|MN|=时,求直线l的方程.
18.(本题满分17分)
如图1,等腰梯形AECD是由三个全等的等边三角形拼成,现△BCE将沿BC翻折至△BCP,使得PD=AB,如图2所示.
⑴求证:PD BC;
⑵在直线PD上是否存在点M,使得直线BM与平面APD所成角的余弦值为 ?若存在,求出的值; 若不存在,说明理由.
19.(本题满分17分)
如图,在平面直角坐标系xOy中,已知椭圆C:(a>b>0)的离心率e=,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
⑴求椭圆C的方程;
⑵已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP EQ,若存在,求出点Q的坐标;若不存在说明理由;
⑶若过O点作直线l的平行线交椭圆C于点M,求的最小值.
试题解析
选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知平面的法向量为(2,-2,4),=(-1,1,-2),则直线AB与平面α的位置关系为( )
A.AB α B.AB α C.AB与α相交但不垂直 D.AB∥α
【答案】A
【解析】∵(2,-2,4),=(-1,1,-2),,∴,∴∥,∴AB α.故选A.
2.直线的倾斜角为( )
A. 75° B.105° C.15° D.60°
【答案】B
【解析】由题意得,直线的斜率, 则直线的倾斜角为105°.故选B.
3.“a=±4”是“圆x2+y2=1与圆x2+(y+a)2=9相切”的( )
A.充分不必要条件 B.必要不充分条件 C. 既不充分也不必要条件 D.充要条件
【答案】A
【解析】若a=±4,则圆x2+y2=1与圆x2+(y+a)2=9相外切;若圆x2+y2=1与圆x2+(y+a)2=9相切,分外切和内切,a不一定等于±4,也可能等于2或-2.所以“a=±4”是“圆x2+y2=1与圆x2+(y+a)2=9相切”的充分不必要条件.故选A.
4.在空间直角坐标系中,已知A(1,0,1),B(1,1,1),C(0,0,),则点A到直线BC的距离为( )
A. 3 B. 5 C. D.
【答案】D
【解析】∵=(0,1,0),,=(-1,-1,),直线BC的方向向量,则点A到直线BC的距离为,故选D.
5.与直线3x-4y+5=0关于x轴对称的直线的方程是( )
A.3x-4y+5=0 B.3x-4y-5=0 C.3x+4y+5=0 D.3x+4y-5=0
【答案】C
【解析】设所求直线上点的坐标(x,y),则关于x轴的对称点的坐标(x,-y)在已知的直线3x-4y+5=0上,∴所求对称直线方程为3x+4y+5=0. 故选C.
6.某广场一个椭球水景雕塑如图所示,其横截面为圆,过横截面圆心的纵截面为椭圆,该椭圆的离心率为.若该椭球的横截面的最大直径为1.8m,则该椭球的高为( )
A.3.2m B.3.4m
C.4m D.3.6m
【答案】D.
【解析】由题意知,e=,∴a=2b,由该椭球的横截面的最大直径为1.8m,可知2b=1.8m,即a=1.8m,该椭球的高2a=3.6m.故选D.
7.如图,正方体ABCD-A1B1C1D1的棱AB和A1D1的中点分别为E,F,则直线EF与
平面AA1D1D所成角的正弦值为 ( )
A. B. C. D.
【答案】C
【解析】以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系, 设正方体ABCD-A1B1C1D1的棱长为2,则E(2,1,0),F(1,0,2),=(-1,-1,2),
平面AA1D1D的法向量n=(0,1,0).
设直线EF与平面AA1D1D所成角为θ,则sin θ=.
所以直线EF与平面AA1D1D所成角的正弦值为.故选C.
8.设O为坐标原点,F1,F2为椭圆C:+=1的两个焦点,点P在C上,cos ∠F1PF2=,则|OP|=( )
A. B. C. D.
【答案】B
【解析】方法1: 依题意a=3,b=,c==.如图,不妨令F1(-,0),F2(,0).设|PF1|=m,|PF2|=n,在△F1PF2中,cos ∠F1PF2== ①,
由椭圆的定义可得m+n=2a=6 ②.
由①②,解得mn=.
设|OP|=x.
在△F1OP和△F2OP中,∠F1OP+∠F2OP=π,
由余弦定理得=-,
得x2===,所以|OP|=.故选B
方法2: 依题意a=3,b=,c==.
如图(图同方法1),设点P的坐标为(x0,y0),α=∠F1PF2,
则cos ∠F1PF2=cos α=,
故sin ∠F1PF2=sin α===,则tan=或tan =2(舍去).
故△F1PF2的面积S△F1PF2=b2tan =6×=3.
又S△F1PF2=×2c|y0|=|y0|,
故y=3,又+=1,
所以x=,|OP|2=x+y=,|OP|=.故选B
方法3: 依题意a=3,b=,c==.
如图(图同方法1),设点P的坐标为(x0,y0),利用焦点三角形面积公式知S△F1PF2=.
因为cos ∠F1PF2=,所以sin ∠F1PF2=,故S△F1PF2==3.又S△F1PF2=×2c|y0|=|y0|,
故y=3,
又+=1,所以x=,|OP|2=x+y=,|OP|=.故选B
方法4: 依题意a=3,b=,c==.
如图(图同方法1),不妨令F1(-,0),F2(,0).
设|PF1|=m,|PF2|=n,在△F1PF2中,cos ∠F1PF2== ①,
由椭圆的定义可得m+n=2a=6 ②.
由①②,解得mn=.
因为=(+),
所以||2=(m2+n2+2mn cos ∠F1PF2)==,所以|PO|=.故选B.
选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,有选错的得0分.若只有两个正确选项,每选对 一个得3分;若只有三个正确选项 ,每选对一个得2分.
9.已知点P是平行四边形ABCD所在的平面外一点,如果=(2,-1,-4),=(4,2,0),=(-1,2,-1).则下列结论正确的是( )
A. AP AB B.AP AD C. 是平面ABCD的法向量 D. ∥
【答案】ABC
【解析】∵=0,=0, ∴AP AB,AP AD,即选项A,B正确;
又与不平行, ∴是平面ABCD的法向量,选项C正确 ;
∵=(2,3,4),=(-1,2,-1),∴与 不平行,选项D错误.
故选ABC.
10.已知直线l:(1-2m)x-(m-1)y+7m-4=0, 圆C:x2+y2-2x-4y-20=0,则以下命题正确 的是( )
A.直线l恒过定点(-3,-1) B.直线l与圆C恒相交
C.圆C被x轴截得的弦长为 D.直线l被圆C截得的弦最短时,
【答案】BC
【解析】依题意,直线l:(1-2m)x-(m-1)y+7m-4=0可化为(-2x-y+7)m+x+y-4=0,
由解得x=3,y=1,即直线l恒过定点P(3,1),选项A错误;
∵圆方程x2+y2-2x-4y-20=0可化为(x-1)2+(y-2)2=25,∴圆C的圆心为C(1,2),半径为r=5,
|PC|=
由于直线l过定点P(3,1),而,∴当直线l被圆C截得的弦最短时,l PC,
=2,即,,则选项D错误.
故选BC.
11.已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线与椭圆C交于A,B两点,且|AB|=3,则( )
A.椭圆的焦点在y轴上 B.△ABF1的周长为6
C.△AF1F2的周长为6 D.椭圆C的方程为=1
【答案】CD
【解析】显然椭圆的焦点在x轴上,A错误.
设椭圆C的方程为=1(a>b>0),c=1.
∵过F2且垂直于x轴的直线与椭圆交于A,B两点,设A(c,y1),
代入方程可得+=1.求得.由于|AB|=3,
∴=,b2=a2-c2,所以a2=4,a=2,b2=a2-c2=4-1=3,
椭圆的方程为=1,△ABF1的周长为4a=8,△AF1F2的周长为2a+2c=6.
故选CD.
填空题:本题共3小题,每小题5分,共15分.
12.圆x2+y2=8内有一点P(2,-1),AB为过点P的弦,则AB的中点Q的轨迹方程为 .
【答案】x2+y2+y-2x=0
【解析】设AB的中点为Q(x,y),则AB的斜率为k=,又OQ⊥AB,
∴kOQ·k=-1,即,整理得x2+y2+y-2x=0,
∴过点P的弦中点的轨迹方程为x2+y2+y-2x=0.
13.已知F1,F2为椭圆C:+=1的两个焦点,P,Q为C上关于坐标原点对称的两点,且|PQ|=|F1F2|,则四边形PF1QF2的面积为________.
【答案】8.
【解析】根据椭圆的对称性及|PQ|=|F1F2|可以得到四边形PF1QF2为对角线相等的平行四边形,所以四边形PF1QF2为矩形.设|PF1|=m,则|PF2|=2a-|PF1|=8-m,则|PF1|2+|PF2|2=m2+(8-m)2=2m2+64-16m=|F1F2|2=4c2=4(a2-b2)=48,得m(8-m)=8,所以四边形PF1QF2的面积为|PF1|×|PF2|=m(8-m)=8.
14.在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体,
该几何体的上、下底面平行,且均为扇环形(扇环是指圆环被扇形截得的部分).
现有一个如图所示的曲池,它的高为2,AA1,BB1,CC1,DD1均与曲池的底面
垂直,底面扇环对应的两个圆的半径分别为1和2,对应的圆心角为90°,则图中异面直线AB1与CD1所成角的余弦值为 .
【答案】
【解析】设上底面圆心为O,下底面圆心为O′,连接OO′,OB,OC,以O为原点,分
别以OC,OB,OO′ 所在直线为x轴,y轴,z轴建立空间直角坐标系,则C(1,0,0),
A(0,2,0),B1(0,1,2),D1(2,0,2),
∴=(0,-1,2),=(1,0,2),
∴.
四、解答题:本题共5道题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.已知△ABC的顶点C(2,-8),直线AB的方程为y=-2x+11,AC边上的高BH所在直线的方程为x+3y+2=0.
⑴求顶点A和B的坐标;
⑵求△ABC外接圆的一般方程.
【答案】⑴A(5,1),B(7,-3); ⑵x2+y2.
【解析】⑴联立,解得,
∴顶点B(7,-3),
∵AC⊥BH,∴kAC·kBH=-1,
已知kBH=-,∴kAC=3,
∴设直线AC的方程为y=3x+b,
将C(2,-8)代入得b=-14,
∴直线AC的方程为y=3x-14.
由,可得顶点A(5,1).
⑵设△ABC的外接圆方程为x2+y2+Dx+Ey+F=0,
将A(5,1),B(7,-3)和C(2,-8)三点的坐标分别代入,得
,解得D=-4,E=6,F=-12,
∴x2+y2
16.如图,已知四棱锥P-ABCD的底面ABCD是矩形,PA 平面ABCD,
PA=AD=2,BD=.
⑴求证:BD 平面PAC;
⑵求二面角P-CD-B的余弦值的大小;
⑶求点C到平面PBD的距离.
【答案】⑴详见解析; ⑵; ⑶
【解析】⑴证明:∵四棱锥P-ABCD的底面ABCD是矩形,PA 平面ABCD,PA=AD=2,BD=.
∴PA BD,AB==2,
∴四边形ABCD为正方形,
∴BD AC,
又AC,PA 平面PAC,AC∩PA=A,
∴BD 平面PAC
⑵方法1:∵四棱锥P-ABCD的底面ABCD是矩形,PA 平面ABCD,PA=AD=2,BD=.
∴PA CD,AD CD,
∴CD 平面PAD,
∴CD PD,
∴∠PDA是二面角P-CD-B的的平面角,
∵PA=AD=2,PA AD,
∴∠PDA=45°,cos∠PDA=cos45°=
∴二面角P-CD-B的余弦值为.
方法2:如图,以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,则C(2,2,0),D(0,2,0),P(0,0,2),
=(2,2,-2),=(0,2,-2),
设平面PCD的法向量=(x,y,z),则
,即,
取y=z=1,x=0,则=(0,1,1),
显然,平面ABCD的法向量=(0,0,1),
设二面角P-CD-B的平面角为θ,则
,
∴二面角P-CD-B的余弦值为.
⑶同⑵方法2建立空间直角坐标系,则
=(2,0,-2),=(2,2,-2),=(0,2,-2),
设平面PBD的法向量=(x0,y0,z0),则
,即,
取x0=y0=z0=1,则=(1,1,1),
∴点C到平面PBD的距离.
17.已知动点P与平面上点A(-1,0),B(1,0)的距离之和等于2.
⑴试求动点P的轨迹方程C;
⑵设直线l: 与曲线C交于M、N两点,当|MN|=时,求直线l的方程.
【答案】⑴;⑵y=x-.
【解析】⑴设动点P的坐标为(x,y),
∵|PA|+|PB|=2>2=|AB|,
∴由椭圆定义可知点P轨迹是以A,B为焦点的椭圆.
∴a=,c=1,b==1,
∴动点P的轨迹方程C为:.
⑵将直线l: 代入椭圆方程得:(1+2k2)x2-4kx+4=0,
∴ =,即k2>1,
设M(x1,y1),N(x2,y2),
∴x1+x2=, ,
∴|MN|=
=.
∴17k4-32k2-57=0,即(17k2+19)(k2-3)=0,
∴k2=3,.
∴直线l的方程为y=x-.
18.如图1,等腰梯形AECD是由三个全等的等边三角形拼成,现△BCE将沿BC翻折至△BCP,使得PD=AB,如图2所示.
⑴求证:PD BC;
⑵在直线PD上是否存在点M,使得直线BM与平面APD所成角的余弦值为 ?若存在,求出的值; 若不存在,说明理由.
【答案】⑴详见解析; ⑵在直线PD上存在点M,使得直线BM与平面APD所成角的余弦值为.此时,的值为2或.
【解析】⑴证明:在图1连接DE交BC于O点,
在图2中,易知△BCD、△BCP 都是等边三角形,
易得DO BC,PO BC,
又DO,PO 平面POD,DO∩PO=O,
∴BC 平面POD,
∴PD BC.
⑵方法1:假设存在点M,符合题意.
设AB=2,则PD=3,
则在△POD中,由OD=OP=,PD=3,由余弦定理得∠POD=120°,
由⑴得BC 平面POD,
又AD∥BC,∴直线AD 平面POD,
∵AD 平面ADP,∴平面ADP 平面POD,
作OQ PD,垂足为Q,则OQ 平面ADP,
在△POD中,由OD=OP=,PD=3,∠POD=120°,
∴OQ=.
如图3,取AP的中点N,连接BN,QN,
由QN∥AD,OB∥AD,得QN∥OB,
又QN=AD=OB,
∴四边形BNQO为平行四边形,
∵OQ 平面ADP,∴BN 平面ADP,
则直线BM与平面APD所成角θ为∠BMN,且BN=OQ=.
由已知得,得,
由BN=BMsin∠BMN=,得BM=,
在△BDM 中,设DM=t,由余弦定理得
,即t2-3t+2=0,
解得t=1或t=2,
∴在直线PD上存在点M,使得直线BM与平面APD所成角的余弦值为.此时,的值为2或.
方法2(等体积法):设AB=2,则PD=3,
则在△POD中,由OD=OP=,PD=3,由余弦定理得∠POD=120°,
作PH DO,垂足为H,连OH,得∠POH=60°,
∴PH=POsin60°=.
由⑴得BC 平面POD,
又AD∥BC,∴直线AD 平面POD,
∴AD PD,即△ADP为直角三角形,
∴△ADP的面积为×AD×PD=×2×3=3,
设点B到平面ADP的距离为h,由VP-ABD=VB-ADP,得
,得h=.
设直线BM与平面APD所成角为θ,则,∴,
∴h=BMsinθ=,得BM=,
在△BDM 中,设DM=t,由余弦定理得
,即t2-3t+2=0,
解得t=1或t=2,
∴在直线PD上存在点M,使得直线BM与平面APD所成角的余弦值为.此时,的值为2或.
方法3(向量法):由方法2知PH=,如图3,以BC的中点O为原点,OB,DO,OZ分别为x,y,z 轴的正方向,建立空间直角坐标系.则B(1,0,0),A(2,,0),D(0,,0),P(0,,).
∴,,
设平面APD的法向量=(x,y,z),则
,即,
解得x=0,令y=-1,得z=,
即=(0,-1,).
设存在点M,,满足题意.
则,
∴,
设直线BM与平面APD所成角为θ,则,∴,
∴.
解得,
∴在直线PD上存在点M,使得直线BM与平面APD所成角的余弦值为.此时,的值为2或.
19.如图,在平面直角坐标系xOy中,已知椭圆C:(a>b>0)的离心率e=,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
⑴求椭圆C的方程;
⑵已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP EQ,若存在,求出点Q的坐标;若不存在说明理由;
⑶若过O点作直线l的平行线交椭圆C于点M,求的最小值.
【答案】⑴; ⑵存在定点Q,对于任意的k(k≠0)都有OP EQ,定点Q的坐标为(-3,0); ⑶当时,的最小值为.
【解析】⑴∵椭圆C:(a>b>0)的离心率e=,左顶点为A(-4,0),
∴a=4,c=2,b2=a2-c2=12.
∴椭圆C的方程为.
⑵直线l的方程为y=k(x+4),
由化简得(x+4)[(4k2+3)x+16k2-12]=0,
∴x1=-4,,
当x=时,,即点D(,),
∵点P为AD的中点,∴点P的坐标为(,),则(k≠0).
对直线l的方程为y=k(x+4),令x=0,得点E坐标为(0,4k),
假设存在定点Q(m,n)(m≠0),使得OP EQ,
则kOPkEQ=-1,即恒成立,
∴(4m+12)k-3n=0恒成立,
∴,即,
∴定点Q的坐标为(-3,0).
⑶∵OM∥l,∴OM的方程可设为y=kx,
由,得点M的横坐标为,
由OM∥l,得
,
当且仅当时,即时取等号,
∴当时,的最小值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
