【人教九上第23章《旋转》中档题专题提优】专题三 旋转作图问题基本方法(1)——中心对称图形(含解析)
文档属性
| 名称 | 【人教九上第23章《旋转》中档题专题提优】专题三 旋转作图问题基本方法(1)——中心对称图形(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 214.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题三 旋转作图问题基本方法(1)——中心对称图形
核心考点一 利用中心对称图形的对称中心构造8字型全等得等线段
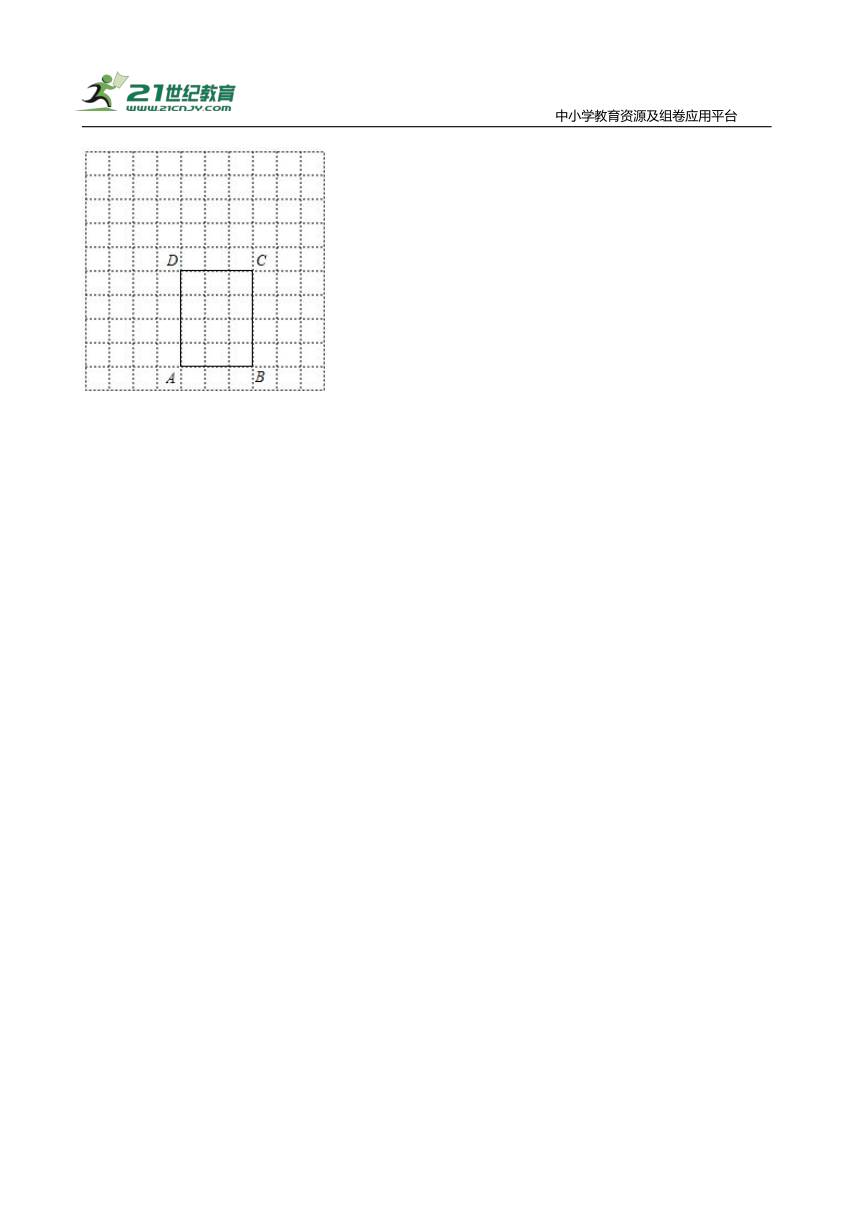
01.如图平行四边形ABCD,E在AD边上,且DE=CD,仅用无刻度直尺作图并保留作图痕迹,不写画法.
(1)在图1中,画出∠C的角平分线,并说明理由;
(2)沿用(1)中解决问题的思路并结合平行四边形的性质,在图2中,画出∠BAD的角平分线,并说明理由.
核心考点二 利用中心对称图形的对称中心得中点,再利用重心或者中位线的性质
02.只用直尺(不带刻度)作图按要求作图,不要求写作法,但要保留作图痕迹.
(1)我们知道,三角形的三条中线交于一点,如图1,在平行四边形中,为的中点,作的中点;
(2)我们知道,三角形的三条高交于一点,如图2,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作的高.
核心考点三 利用过中心对称图形的对称中心的直线分割面积
03.如图,在每个小正方形的边长均为1的网格中,点A,B,C,D均在格点上,请在此网格中仅用无刻度的直尺画图(保留连线痕迹).
(1)画出线段BE,使BE∥AC,且BE=AC;
(2)画出以AC为边的正方形ACMN;
(3)在(1)的条件下,画出直线PQ,使PQ平分四边形ABED的面积(作出一条即可).
专题三 旋转作图问题基本方法(1)——中心对称图形
核心考点一 利用中心对称图形的对称中心构造8字型全等得等线段
01.如图平行四边形ABCD,E在AD边上,且DE=CD,仅用无刻度直尺作图并保留作图痕迹,不写画法.
(1)在图1中,画出∠C的角平分线,并说明理由;
(2)沿用(1)中解决问题的思路并结合平行四边形的性质,在图2中,画出∠BAD的角平分线,并说明理由.
解:(1)如图1,∵DE=DC,
∴∠DEC=∠DCE,
∵AD∥BC,
∴∠DEC=∠BCE,
则∠DCE=∠BCE,
即CE平分∠BCD,
则CE为所求作;
(2)如图2,延长EO交BC于F,则AF为所作.
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,OD=OB,AB=CD,
∴∠EDO=∠FBO,∠EOD=∠FOB,
∴△BOF≌△DOE(ASA),
又∵DE=CD,
∴BF=DE=CD=AB,
∴∠BAF=∠BFA=∠FAD,
则AF是所求作的角平分线.
核心考点二 利用中心对称图形的对称中心得中点,再利用重心或者中位线的性质
02.只用直尺(不带刻度)作图按要求作图,不要求写作法,但要保留作图痕迹.
(1)我们知道,三角形的三条中线交于一点,如图1,在平行四边形中,为的中点,作的中点;
(2)我们知道,三角形的三条高交于一点,如图2,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作的高.
解:(1)如图1中,四边形ABCD即为所求;
(2)如图2中,线段AH即为所求.
核心考点三 利用过中心对称图形的对称中心的直线分割面积
03.如图,在每个小正方形的边长均为1的网格中,点A,B,C,D均在格点上,请在此网格中仅用无刻度的直尺画图(保留连线痕迹).
(1)画出线段BE,使BE∥AC,且BE=AC;
(2)画出以AC为边的正方形ACMN;
(3)在(1)的条件下,画出直线PQ,使PQ平分四边形ABED的面积(作出一条即可).
解:(1)如图所示BE即为所作;
(2)如图所示ACMN即为所作;
(3)如图所示,作线段AB的中点G,作直线CG,直线CG即为所作直线PQ.
专题三 旋转作图问题基本方法(1)——中心对称图形
核心考点一 利用中心对称图形的对称中心构造8字型全等得等线段
01.如图平行四边形ABCD,E在AD边上,且DE=CD,仅用无刻度直尺作图并保留作图痕迹,不写画法.
(1)在图1中,画出∠C的角平分线,并说明理由;
(2)沿用(1)中解决问题的思路并结合平行四边形的性质,在图2中,画出∠BAD的角平分线,并说明理由.
核心考点二 利用中心对称图形的对称中心得中点,再利用重心或者中位线的性质
02.只用直尺(不带刻度)作图按要求作图,不要求写作法,但要保留作图痕迹.
(1)我们知道,三角形的三条中线交于一点,如图1,在平行四边形中,为的中点,作的中点;
(2)我们知道,三角形的三条高交于一点,如图2,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作的高.
核心考点三 利用过中心对称图形的对称中心的直线分割面积
03.如图,在每个小正方形的边长均为1的网格中,点A,B,C,D均在格点上,请在此网格中仅用无刻度的直尺画图(保留连线痕迹).
(1)画出线段BE,使BE∥AC,且BE=AC;
(2)画出以AC为边的正方形ACMN;
(3)在(1)的条件下,画出直线PQ,使PQ平分四边形ABED的面积(作出一条即可).
专题三 旋转作图问题基本方法(1)——中心对称图形
核心考点一 利用中心对称图形的对称中心构造8字型全等得等线段
01.如图平行四边形ABCD,E在AD边上,且DE=CD,仅用无刻度直尺作图并保留作图痕迹,不写画法.
(1)在图1中,画出∠C的角平分线,并说明理由;
(2)沿用(1)中解决问题的思路并结合平行四边形的性质,在图2中,画出∠BAD的角平分线,并说明理由.
解:(1)如图1,∵DE=DC,
∴∠DEC=∠DCE,
∵AD∥BC,
∴∠DEC=∠BCE,
则∠DCE=∠BCE,
即CE平分∠BCD,
则CE为所求作;
(2)如图2,延长EO交BC于F,则AF为所作.
理由:∵四边形ABCD是平行四边形,
∴AD∥BC,OD=OB,AB=CD,
∴∠EDO=∠FBO,∠EOD=∠FOB,
∴△BOF≌△DOE(ASA),
又∵DE=CD,
∴BF=DE=CD=AB,
∴∠BAF=∠BFA=∠FAD,
则AF是所求作的角平分线.
核心考点二 利用中心对称图形的对称中心得中点,再利用重心或者中位线的性质
02.只用直尺(不带刻度)作图按要求作图,不要求写作法,但要保留作图痕迹.
(1)我们知道,三角形的三条中线交于一点,如图1,在平行四边形中,为的中点,作的中点;
(2)我们知道,三角形的三条高交于一点,如图2,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作的高.
解:(1)如图1中,四边形ABCD即为所求;
(2)如图2中,线段AH即为所求.
核心考点三 利用过中心对称图形的对称中心的直线分割面积
03.如图,在每个小正方形的边长均为1的网格中,点A,B,C,D均在格点上,请在此网格中仅用无刻度的直尺画图(保留连线痕迹).
(1)画出线段BE,使BE∥AC,且BE=AC;
(2)画出以AC为边的正方形ACMN;
(3)在(1)的条件下,画出直线PQ,使PQ平分四边形ABED的面积(作出一条即可).
解:(1)如图所示BE即为所作;
(2)如图所示ACMN即为所作;
(3)如图所示,作线段AB的中点G,作直线CG,直线CG即为所作直线PQ.
同课章节目录
