1.6有理数的乘方(第1课时) 课件(共18张PPT)
文档属性
| 名称 | 1.6有理数的乘方(第1课时) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 12:52:49 | ||
图片预览






文档简介
(共18张PPT)
2024-09-24
沪科版(2024)七年级数学上册 第一章有理数
1.6 有理数的乘方
第一课时 有理数的乘方
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
若对折100次,算式中有几个2相乘?
对折2次可裁成4张,即2×2张;
对折3次可裁成8张,即2×2×2张;
试一试:将一张纸按下列要求对折。
情景导入
对折10次裁成的张数用以下算式计算
对折100次裁成的张数,可用算式
计算,在这个积中有100个2相乘。
2×2×2×2×2×2×2×2×2×2
是一个有10个2相乘的乘积式;
思考:这么长的算式有简单的记法吗?
(2)如图,边长为2 的立方体,它的体积是: ,可记: 。
(1)如图,边长为2的正方形,它的面积是_________,可记作: 。
22
23
2×2×2=8
2×2= 4
2
2
2
体积
2
2
面积
2×2×2×2 可记作: ,
2×2×2×2×2 可记 作: ,
2×2×···×2
n个2
可记作: ,
a · a · a · … · a 可记作: , 即a · a · a · … · a= .
n个a
n个a
24
25
2n
an
an
想一想:上面各式具有什么共同特征?
猜想:
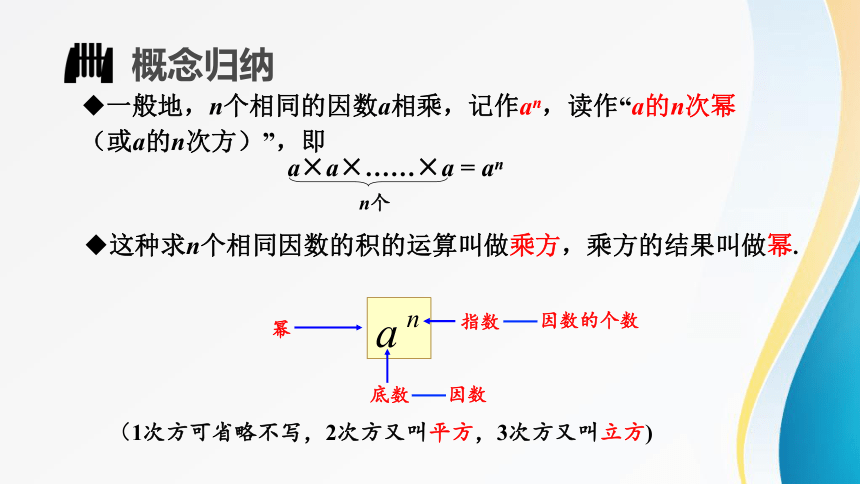
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
(1次方可省略不写,2次方又叫平方,3次方又叫立方)
a×a×……×a = an
n个
幂
指数
因数的个数
底数
因数
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
概念归纳
运算 加法 减法 乘法 除法 乘方
结果
幂
和
差
积
商
五种运算及其运算结果的名称
1.(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示 个 相乘,读作 的 次方,也读作 的 次幂,其中 叫做 ,6叫做 .
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
练一练
1.乘方的意义及运算
新知探究
横、纵向观察你发现有理数的幂有什么规律?
例1
1.计算(先确定符号,再算结果):
(1)(-1.5) ; (2)4 ×(-2) ;
(3); (4)(-2) ×(-2) .
练一练
(-3)2 -32
议一议:(-3)2与-32有什么不同?结果相等吗?
有括号
无括号
-3的平方
3的平方的相反数
2个(-3)相乘
即(-3)×(-3)
2个3相乘的积的相反数
即-(3×3)
-9
写法
读法
意义
结果
9
注意:底数是负数或分数时,必须加上括号.
练一练
2.在计算时,有的同学认为结果为 22+=4,
有的同学认为先化带分数为假分数,再乘方,
即==.
通过计算,你认为哪种看法是正确的?
3.口答:
(1)13 (2)12024
(3)(-1)8 (4)(-1)2024
(5)(-1)7 (6)(-1)2025
练一练
(1)1的任何次幂都为1;
(2)-1的幂很有规律:
-1的奇次幂是-1, -1的偶次幂是1.
概念归纳
练习:(-1)n
解析:(-1)n= .
(当n为奇数时)
(当n为偶数时)
观察上述结果,你发现了什么规律?
100
1000
10000
100000
100
-1000
10000
-100000
做一做
1.底数为10的幂的特点:
10的几次幂,1的后面就有几个0.
2.有理数乘方运算的符号法则:
正数的任何次幂都是正数;
负数的偶数次幂是正数,奇数次幂是负数.
3.互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
总结归纳
2.如果 x-3 +(y+2)2=0,求y x的值.
且 |x-3| +(y+2)2=0,
解:∵ |x-3| ≥0,(y+2)2≥0
∴ |x-3| =0,(y+2)2=0,
∴x=3,y=-2,
∴y x=(-2)3=-8.
方法总结:几个非负数的和为0,则这几个数都等于0.
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正整数次幂都是零.
幂
指数
底数
课堂小结
2024-09-24
沪科版(2024)七年级数学上册 第一章有理数
1.6 有理数的乘方
第一课时 有理数的乘方
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
若对折100次,算式中有几个2相乘?
对折2次可裁成4张,即2×2张;
对折3次可裁成8张,即2×2×2张;
试一试:将一张纸按下列要求对折。
情景导入
对折10次裁成的张数用以下算式计算
对折100次裁成的张数,可用算式
计算,在这个积中有100个2相乘。
2×2×2×2×2×2×2×2×2×2
是一个有10个2相乘的乘积式;
思考:这么长的算式有简单的记法吗?
(2)如图,边长为2 的立方体,它的体积是: ,可记: 。
(1)如图,边长为2的正方形,它的面积是_________,可记作: 。
22
23
2×2×2=8
2×2= 4
2
2
2
体积
2
2
面积
2×2×2×2 可记作: ,
2×2×2×2×2 可记 作: ,
2×2×···×2
n个2
可记作: ,
a · a · a · … · a 可记作: , 即a · a · a · … · a= .
n个a
n个a
24
25
2n
an
an
想一想:上面各式具有什么共同特征?
猜想:
这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
(1次方可省略不写,2次方又叫平方,3次方又叫立方)
a×a×……×a = an
n个
幂
指数
因数的个数
底数
因数
一般地,n个相同的因数a相乘,记作an,读作“a的n次幂(或a的n次方)”,即
概念归纳
运算 加法 减法 乘法 除法 乘方
结果
幂
和
差
积
商
五种运算及其运算结果的名称
1.(1)(-5)2的底数是_____,指数是_____,(-5)2表示2个_____相乘,读作_____的2次方,也读作-5的_____.
(2) 表示 个 相乘,读作 的 次方,也读作 的 次幂,其中 叫做 ,6叫做 .
温馨提示:幂的底数是分数或负数时,底数应该添上括号!
练一练
1.乘方的意义及运算
新知探究
横、纵向观察你发现有理数的幂有什么规律?
例1
1.计算(先确定符号,再算结果):
(1)(-1.5) ; (2)4 ×(-2) ;
(3); (4)(-2) ×(-2) .
练一练
(-3)2 -32
议一议:(-3)2与-32有什么不同?结果相等吗?
有括号
无括号
-3的平方
3的平方的相反数
2个(-3)相乘
即(-3)×(-3)
2个3相乘的积的相反数
即-(3×3)
-9
写法
读法
意义
结果
9
注意:底数是负数或分数时,必须加上括号.
练一练
2.在计算时,有的同学认为结果为 22+=4,
有的同学认为先化带分数为假分数,再乘方,
即==.
通过计算,你认为哪种看法是正确的?
3.口答:
(1)13 (2)12024
(3)(-1)8 (4)(-1)2024
(5)(-1)7 (6)(-1)2025
练一练
(1)1的任何次幂都为1;
(2)-1的幂很有规律:
-1的奇次幂是-1, -1的偶次幂是1.
概念归纳
练习:(-1)n
解析:(-1)n= .
(当n为奇数时)
(当n为偶数时)
观察上述结果,你发现了什么规律?
100
1000
10000
100000
100
-1000
10000
-100000
做一做
1.底数为10的幂的特点:
10的几次幂,1的后面就有几个0.
2.有理数乘方运算的符号法则:
正数的任何次幂都是正数;
负数的偶数次幂是正数,奇数次幂是负数.
3.互为相反数的相同偶次幂相等,相同奇次幂互为相反数.
总结归纳
2.如果 x-3 +(y+2)2=0,求y x的值.
且 |x-3| +(y+2)2=0,
解:∵ |x-3| ≥0,(y+2)2≥0
∴ |x-3| =0,(y+2)2=0,
∴x=3,y=-2,
∴y x=(-2)3=-8.
方法总结:几个非负数的和为0,则这几个数都等于0.
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数,负数的偶次幂是正数;
(3)零的正整数次幂都是零.
幂
指数
底数
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
