2.3整式的概念(第1课时整式)课件(共30张PPT)-七年级数学上册(湘教版2024)
文档属性
| 名称 | 2.3整式的概念(第1课时整式)课件(共30张PPT)-七年级数学上册(湘教版2024) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
湘教版(2024)七年级数学上册 第二章 代数式
2.3.1 整式
2.3 整式的概念
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
理解单项式、多项式和整式的概念,掌握单项式系
数、次数以及多项式项、次数的概念.
2. 能准确地确定一个单项式的系数和次数以及一个多
项式的次数和项数.
情景导入
据了解“天宫一号”在太空中绕地球飞行的速度约为7.5千米每秒.绕地球一圈只需要一个小时.
“天宫一号”飞行10秒能飞_____千米;飞行1分钟能飞_____千米;飞行 t 秒能飞_____千米.
75
450
7.5 t
新知探究
下面下划线上的代数式里含有加减运算吗 只含有哪些运算
(1) 以 8 km/h 的平均速度行走 t h 的路程是 ;
(2) 半径为 r 的圆的面积是 ;
(3) 底面是边长为 x 的正方形,高为 y 的长方体的体积是 .
8t
πr2
x2y
我们知道,8t表示8与t的积,πr2表示π与r2的积,x2y表示x2与y的积. 这三个代数式均不含加减运算,只含有数与字母的幂的乘法运算.
新知探究
由数与字母及其幂的乘积组成的代数式叫作单项式,其中这个数叫作单项式的系数,所有字母的指数的和叫作单项式的次数 .
当单项式的系数为“1” 或“-1”时,“1”省略不写.
例 如 , x, 8t, πr2 , -x2y都 是 单 项 式 . 其中,x 的系数是 1,次数是 1;8t 的 系数是 8,次数是 1; πr2的系数是 π,次数是2; -x2y的系数是-1,次数是3.
单独一个数也可看作单项式,并约定一个不为0的数其次数为0.
做一做
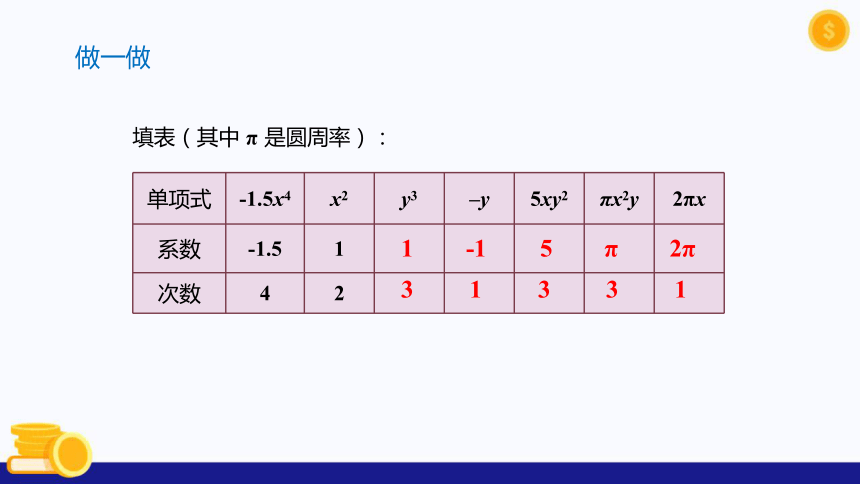
填表(其中 π 是圆周率):
单项式 -1.5x4 x2 y3 –y 5xy2 πx2y 2πx
系数 -1.5 1
次数 4 2
1
3
-1
1
5
3
π
3
2π
1
说一说
右图是由一个长方形和一个半圆组成. 已知长方形的长为 x,宽为 y,半圆的直径为y.
(1) 长方形的面积为多少?
(2) 半圆的面积为多少?
(3) 由长方形和半圆组成的图形的面积为多少?
y
x
xy
y2
xy + y2
从这个例子受到启发,有时需要考虑几个单项式的和.
概念归纳
几个单项式的和叫作多项式,其中的每个单项式叫作多项式的项,不含字 母的项叫作常数项,次数最高的项的次数叫作这个多项式的次数.
单项式与多项式统称为整式.
由数与字母及其幂的乘积组成的代数式叫作单项式,其中这个数叫作单项式的系数,所有字母的指数的和叫作单项式的次数 .
课本例题
例1 分别写出下列多项式的次数和常数项:
(1)2x-3; (2)-x3+7x -4;
(3)3x2 -5xy + y2-4x + 6y -9 .
解 (1)2x-3 的次数是 1 ,常数项是-3 .
(2)-x3+7x -4 的次数是 3 ,常数项是-4 .
(3)3x2 -5xy + y2-4x + 6y -9 的次数是 2 ,常数项是-9 .
课堂练习
1.填表(其中 π 是圆周率):
单项式 x4 2 000x2 –x πx3 4xy5 –6x4y2
系数
次数
4
2
2 000
1
-1
3
π
6
4
6
-6
2.分别写出下列多项式的次数和常数项.
(1)-3x +11;
(2)- x2 + 4x -7;
(3)x3-2x2y -3x+ y2 + 5y -1;
(4)-x4+ 5x2y3 -12xy + y2-2y + 25 .
次数:1 ;常数项:11 .
次数:2 ;常数项:-7 .
次数:3 ;常数项:-1 .
次数:5 ;常数项:25 .
分层练习-基础
知识点1 单项式及相关概念
1. 在- a , , , , m3 n2, xy -1,0, 中,是单
项式的有( B )
A. 6个 B. 5个
C. 4个 D. 3个
B
2. 下列说法中,正确的是( )
A. a 的系数为0
B. π xy3的系数为 π
C. ab2 c 的次数是2
D. -5是一次单项式
【点拨】
a 的系数为1,故A不符合题意; π xy3的系数是 π,
故B符合题意; ab2 c 的次数是4,故C不符合题意;-5是
零次单项式,故D不符合题意.
B
3. [2023江西]单项式-5 ab 的系数为 .
4. [新视角·结论开放题]请写出一个含有字母 a , b ,且次数
是5的单项式: .
-5
ab4(答案不唯一)
知识点2 多项式及相关概念
5. 在 x2-2,-1,-2 x -1,π, , x2+ +1,4 x 中,
多项式有( C )
A. 1个 B. 2个
C. 3个 D. 4个
【点拨】
多项式有 x2-2,-2 x -1, .对于 x2+ +1,由
于 不是单项式,所以 x2+ +1不是多项式.
C
6. [2024成都青羊区模拟]多项式1+2 xy -3 xy2的次数及最高次项的系数分别是( A )
A. 3,-3 B. 2,-3
C. 5,-3 D. 2,3
A
7. 若多项式 xy| m- n|+( n -2) x2 y2+1是关于 x , y 的三次多项式,则 mn = .
【点拨】
因为多项式 xy| m- n|+( n -2) x2 y2+1是关于 x , y 的三次多项式,
所以 n -2=0,1+| m - n |=3.
所以 n =2,| m - n |=2.
所以 m - n =2或 n - m =2.
所以 m =4或 m =0.所以 mn =0或8.
0或8
知识点3 整式及整式的值
8. 把下列各式分别填在相应的大括号里.
4, , + b ,π R2-π r2, x2,2 x -3,- x2+ yz , a2+ +2.
单项式:{4, x2};
4, x2
多项式:{ + b ,π R2-π r2,2 x -3,- x2+ yz };
整式:{4, + b ,π R2-π r2, x2,2 x -3,- x2+ yz }.
+ b ,π R2-π r2,2 x -3,- x2+ yz
4, + b ,π R2-π r2, x2,2 x -3,- x2+ yz
9. [易错题]下列说法错误的是( )
A. m 是单项式也是整式
B. ( m - n )是多项式也是整式
C. 整式一定是单项式
D. 整式不一定是多项式
C
10. [新考法·整体求值法23南通]若 a2-4 a -12=0,则2 a2-8 a -8的值为( )
A. 24 B. 20
C. 18 D. 16
D
11. [2023重庆]用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,…,按此规律排列下去,则第⑧个图案用的木棍根数是( B )
A. 39 B. 44
C. 49 D. 54
【点拨】
由题图可得,图案①有4+5=9根木棍,
图案②有4+5×2=14根木棍,
图案③有4+5×3=19根木棍,
…
所以第 个图案有(4+5 n )根木棍.
所以第⑧个图案有4+5×8=44根木棍.
故选B.
B
【答案】
易错点 确定多项式各项及各项系数时,因易漏掉前面的符号而出错
12. 对于多项式-3 x -2 xy2-1,下列说法中,正确的是
( C )
A. 一次项系数是3 B. 最高次项是2 xy2
C. 常数项是-1 D. 是四次三项式
【点拨】
多项式的每一项都是单项式,且每一项都包括它前
面的符号,特别是单项式的符号为负号时,一定不要漏
掉该项的符号.
C
分层练习-巩固
利用单项式的相关概念求字母的值
13. (1)已知单项式6 x2 y4与- a2 bm+2的次数相同,求 m2-2 m 的值;
【解】根据题意,得 m +2+2=2+4,
解得 m =2.所以 m2-2 m =22-2×2=0.
(2)若 x2 yn+1是关于 x , y 的五次单项式且系数为1,试求 m , n 的值.
【解】由题意得 n +1+2=5,且3 m +3=1,
解得 m =- , n =2.
利用整式的相关定义求字母的值
14. [2024岳阳岳化三中模拟]已知关于 x 的整式( k2-9) x3+( k -3) x2- k .
(1)若该整式是二次式,求 k2+2 k +1的值;
【解】由题意,知 k2-9=0且 k -3≠0,
所以 k =-3. 则 k2+2 k +1=(-3)2+2×(-3)+1=4.
(2)若该整式是二项式,求 k 的值.
【解】当 k =0时,原式=-9 x3-3 x2,符合题意.
当 k2-9=0时, k =±3.
当 k =3时,原式=-3,不符合题意,舍去;
当 k =-3时,原式=-6 x2+3,符合题意.
综上, k =-3或0.
15. 已知关于 x 的多项式3 x4-( m +5) x3+( n -1) x2-5 x +3
不含 x3项和 x2项,求 m +2 n 的值.
【解】由题意知,-( m +5)=0, n -1=0,
解得 m =-5, n =1.
所以 m +2 n =-5+2×1=-3.
分层练习-拓展
利用求整式的值探求实际中的应用问题
16. [新趋势·跨学科综合]如图是某种杆秤.在秤杆的点 A 处固定提纽,点 B 处挂秤盘,点 C 为0刻度点,当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点 C ,秤杆处于平衡.秤盘放入 x g物品后移动秤砣,当秤砣所挂位置与提纽的距离为 y mm时秤杆处于平衡,测得 x 与 y 的几组对应数据如下表:
x/ g 0 2 4 6 10
y/ mm 10 14 18 22 30
由表中数据的规律可知,当 x =20时, y = .
50
由题可得,
当放入0 g物品时,秤砣所挂位置与提纽的距离为10 mm,
当放入2 g物品时,秤砣所挂位置与提纽的距离为10+2×2=14(mm),
当放入4 g物品时,秤砣所挂位置与提纽的距离为10+2×4=18(mm),
【点拨】
当放入6 g物品时,秤砣所挂位置与提纽的距离为10+2×6=22(mm),
当放入8 g物品时,秤砣所挂位置与提纽的距离为10+2×8=26(mm),
当放入10 g物品时,秤砣所挂位置与提纽的距离为10+2×10=30(mm),
…
所以当放入 x g物品时,秤砣所挂位置与提纽的距离为(10+2 x )mm.
所以当放入20 g物品时,秤砣所挂位置与提纽的距离为10+2×20=50(mm).
利用整式探求排列规律
17. [新考法归纳法2023安徽][观察思考]
[规律发现]
请用含 n 的式子填空:
(1)第 n 个图案中“◎”的个数为 ;
3 n
(2)第1个图案中“★”的个数可表示为 ,第2个图案
中“★”的个数可表示为 ,第3个图案中“★”的
个数可表示为 ,第4个图案中“★”的个数可表示
为 ,
…
则第 n 个图案中“★”的个数可表示为 .
课堂小结
整式
单项式
多项式
次数
常数项
次数
系数
定义
定义
由数与字母及其幂的乘积组成的代数式叫作单项式
单项式中这个数叫作单项式的系数
单项式中所有字母的指数的和叫作单项式的次数
几个单项式的和叫作多项式
多项式中不含字母的项叫作常数项
多项式中次数最高的项的次数叫作这个多项式的次数
湘教版(2024)七年级数学上册 第二章 代数式
2.3.1 整式
2.3 整式的概念
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
理解单项式、多项式和整式的概念,掌握单项式系
数、次数以及多项式项、次数的概念.
2. 能准确地确定一个单项式的系数和次数以及一个多
项式的次数和项数.
情景导入
据了解“天宫一号”在太空中绕地球飞行的速度约为7.5千米每秒.绕地球一圈只需要一个小时.
“天宫一号”飞行10秒能飞_____千米;飞行1分钟能飞_____千米;飞行 t 秒能飞_____千米.
75
450
7.5 t
新知探究
下面下划线上的代数式里含有加减运算吗 只含有哪些运算
(1) 以 8 km/h 的平均速度行走 t h 的路程是 ;
(2) 半径为 r 的圆的面积是 ;
(3) 底面是边长为 x 的正方形,高为 y 的长方体的体积是 .
8t
πr2
x2y
我们知道,8t表示8与t的积,πr2表示π与r2的积,x2y表示x2与y的积. 这三个代数式均不含加减运算,只含有数与字母的幂的乘法运算.
新知探究
由数与字母及其幂的乘积组成的代数式叫作单项式,其中这个数叫作单项式的系数,所有字母的指数的和叫作单项式的次数 .
当单项式的系数为“1” 或“-1”时,“1”省略不写.
例 如 , x, 8t, πr2 , -x2y都 是 单 项 式 . 其中,x 的系数是 1,次数是 1;8t 的 系数是 8,次数是 1; πr2的系数是 π,次数是2; -x2y的系数是-1,次数是3.
单独一个数也可看作单项式,并约定一个不为0的数其次数为0.
做一做
填表(其中 π 是圆周率):
单项式 -1.5x4 x2 y3 –y 5xy2 πx2y 2πx
系数 -1.5 1
次数 4 2
1
3
-1
1
5
3
π
3
2π
1
说一说
右图是由一个长方形和一个半圆组成. 已知长方形的长为 x,宽为 y,半圆的直径为y.
(1) 长方形的面积为多少?
(2) 半圆的面积为多少?
(3) 由长方形和半圆组成的图形的面积为多少?
y
x
xy
y2
xy + y2
从这个例子受到启发,有时需要考虑几个单项式的和.
概念归纳
几个单项式的和叫作多项式,其中的每个单项式叫作多项式的项,不含字 母的项叫作常数项,次数最高的项的次数叫作这个多项式的次数.
单项式与多项式统称为整式.
由数与字母及其幂的乘积组成的代数式叫作单项式,其中这个数叫作单项式的系数,所有字母的指数的和叫作单项式的次数 .
课本例题
例1 分别写出下列多项式的次数和常数项:
(1)2x-3; (2)-x3+7x -4;
(3)3x2 -5xy + y2-4x + 6y -9 .
解 (1)2x-3 的次数是 1 ,常数项是-3 .
(2)-x3+7x -4 的次数是 3 ,常数项是-4 .
(3)3x2 -5xy + y2-4x + 6y -9 的次数是 2 ,常数项是-9 .
课堂练习
1.填表(其中 π 是圆周率):
单项式 x4 2 000x2 –x πx3 4xy5 –6x4y2
系数
次数
4
2
2 000
1
-1
3
π
6
4
6
-6
2.分别写出下列多项式的次数和常数项.
(1)-3x +11;
(2)- x2 + 4x -7;
(3)x3-2x2y -3x+ y2 + 5y -1;
(4)-x4+ 5x2y3 -12xy + y2-2y + 25 .
次数:1 ;常数项:11 .
次数:2 ;常数项:-7 .
次数:3 ;常数项:-1 .
次数:5 ;常数项:25 .
分层练习-基础
知识点1 单项式及相关概念
1. 在- a , , , , m3 n2, xy -1,0, 中,是单
项式的有( B )
A. 6个 B. 5个
C. 4个 D. 3个
B
2. 下列说法中,正确的是( )
A. a 的系数为0
B. π xy3的系数为 π
C. ab2 c 的次数是2
D. -5是一次单项式
【点拨】
a 的系数为1,故A不符合题意; π xy3的系数是 π,
故B符合题意; ab2 c 的次数是4,故C不符合题意;-5是
零次单项式,故D不符合题意.
B
3. [2023江西]单项式-5 ab 的系数为 .
4. [新视角·结论开放题]请写出一个含有字母 a , b ,且次数
是5的单项式: .
-5
ab4(答案不唯一)
知识点2 多项式及相关概念
5. 在 x2-2,-1,-2 x -1,π, , x2+ +1,4 x 中,
多项式有( C )
A. 1个 B. 2个
C. 3个 D. 4个
【点拨】
多项式有 x2-2,-2 x -1, .对于 x2+ +1,由
于 不是单项式,所以 x2+ +1不是多项式.
C
6. [2024成都青羊区模拟]多项式1+2 xy -3 xy2的次数及最高次项的系数分别是( A )
A. 3,-3 B. 2,-3
C. 5,-3 D. 2,3
A
7. 若多项式 xy| m- n|+( n -2) x2 y2+1是关于 x , y 的三次多项式,则 mn = .
【点拨】
因为多项式 xy| m- n|+( n -2) x2 y2+1是关于 x , y 的三次多项式,
所以 n -2=0,1+| m - n |=3.
所以 n =2,| m - n |=2.
所以 m - n =2或 n - m =2.
所以 m =4或 m =0.所以 mn =0或8.
0或8
知识点3 整式及整式的值
8. 把下列各式分别填在相应的大括号里.
4, , + b ,π R2-π r2, x2,2 x -3,- x2+ yz , a2+ +2.
单项式:{4, x2};
4, x2
多项式:{ + b ,π R2-π r2,2 x -3,- x2+ yz };
整式:{4, + b ,π R2-π r2, x2,2 x -3,- x2+ yz }.
+ b ,π R2-π r2,2 x -3,- x2+ yz
4, + b ,π R2-π r2, x2,2 x -3,- x2+ yz
9. [易错题]下列说法错误的是( )
A. m 是单项式也是整式
B. ( m - n )是多项式也是整式
C. 整式一定是单项式
D. 整式不一定是多项式
C
10. [新考法·整体求值法23南通]若 a2-4 a -12=0,则2 a2-8 a -8的值为( )
A. 24 B. 20
C. 18 D. 16
D
11. [2023重庆]用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了9根木棍,第②个图案用了14根木棍,第③个图案用了19根木棍,第④个图案用了24根木棍,…,按此规律排列下去,则第⑧个图案用的木棍根数是( B )
A. 39 B. 44
C. 49 D. 54
【点拨】
由题图可得,图案①有4+5=9根木棍,
图案②有4+5×2=14根木棍,
图案③有4+5×3=19根木棍,
…
所以第 个图案有(4+5 n )根木棍.
所以第⑧个图案有4+5×8=44根木棍.
故选B.
B
【答案】
易错点 确定多项式各项及各项系数时,因易漏掉前面的符号而出错
12. 对于多项式-3 x -2 xy2-1,下列说法中,正确的是
( C )
A. 一次项系数是3 B. 最高次项是2 xy2
C. 常数项是-1 D. 是四次三项式
【点拨】
多项式的每一项都是单项式,且每一项都包括它前
面的符号,特别是单项式的符号为负号时,一定不要漏
掉该项的符号.
C
分层练习-巩固
利用单项式的相关概念求字母的值
13. (1)已知单项式6 x2 y4与- a2 bm+2的次数相同,求 m2-2 m 的值;
【解】根据题意,得 m +2+2=2+4,
解得 m =2.所以 m2-2 m =22-2×2=0.
(2)若 x2 yn+1是关于 x , y 的五次单项式且系数为1,试求 m , n 的值.
【解】由题意得 n +1+2=5,且3 m +3=1,
解得 m =- , n =2.
利用整式的相关定义求字母的值
14. [2024岳阳岳化三中模拟]已知关于 x 的整式( k2-9) x3+( k -3) x2- k .
(1)若该整式是二次式,求 k2+2 k +1的值;
【解】由题意,知 k2-9=0且 k -3≠0,
所以 k =-3. 则 k2+2 k +1=(-3)2+2×(-3)+1=4.
(2)若该整式是二项式,求 k 的值.
【解】当 k =0时,原式=-9 x3-3 x2,符合题意.
当 k2-9=0时, k =±3.
当 k =3时,原式=-3,不符合题意,舍去;
当 k =-3时,原式=-6 x2+3,符合题意.
综上, k =-3或0.
15. 已知关于 x 的多项式3 x4-( m +5) x3+( n -1) x2-5 x +3
不含 x3项和 x2项,求 m +2 n 的值.
【解】由题意知,-( m +5)=0, n -1=0,
解得 m =-5, n =1.
所以 m +2 n =-5+2×1=-3.
分层练习-拓展
利用求整式的值探求实际中的应用问题
16. [新趋势·跨学科综合]如图是某种杆秤.在秤杆的点 A 处固定提纽,点 B 处挂秤盘,点 C 为0刻度点,当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点 C ,秤杆处于平衡.秤盘放入 x g物品后移动秤砣,当秤砣所挂位置与提纽的距离为 y mm时秤杆处于平衡,测得 x 与 y 的几组对应数据如下表:
x/ g 0 2 4 6 10
y/ mm 10 14 18 22 30
由表中数据的规律可知,当 x =20时, y = .
50
由题可得,
当放入0 g物品时,秤砣所挂位置与提纽的距离为10 mm,
当放入2 g物品时,秤砣所挂位置与提纽的距离为10+2×2=14(mm),
当放入4 g物品时,秤砣所挂位置与提纽的距离为10+2×4=18(mm),
【点拨】
当放入6 g物品时,秤砣所挂位置与提纽的距离为10+2×6=22(mm),
当放入8 g物品时,秤砣所挂位置与提纽的距离为10+2×8=26(mm),
当放入10 g物品时,秤砣所挂位置与提纽的距离为10+2×10=30(mm),
…
所以当放入 x g物品时,秤砣所挂位置与提纽的距离为(10+2 x )mm.
所以当放入20 g物品时,秤砣所挂位置与提纽的距离为10+2×20=50(mm).
利用整式探求排列规律
17. [新考法归纳法2023安徽][观察思考]
[规律发现]
请用含 n 的式子填空:
(1)第 n 个图案中“◎”的个数为 ;
3 n
(2)第1个图案中“★”的个数可表示为 ,第2个图案
中“★”的个数可表示为 ,第3个图案中“★”的
个数可表示为 ,第4个图案中“★”的个数可表示
为 ,
…
则第 n 个图案中“★”的个数可表示为 .
课堂小结
整式
单项式
多项式
次数
常数项
次数
系数
定义
定义
由数与字母及其幂的乘积组成的代数式叫作单项式
单项式中这个数叫作单项式的系数
单项式中所有字母的指数的和叫作单项式的次数
几个单项式的和叫作多项式
多项式中不含字母的项叫作常数项
多项式中次数最高的项的次数叫作这个多项式的次数
同课章节目录
