4.2合并同类项(第1课时)(同步课件)-七年级数学上册同步精品课堂(青岛版2024)
文档属性
| 名称 | 4.2合并同类项(第1课时)(同步课件)-七年级数学上册同步精品课堂(青岛版2024) |

|
|
| 格式 | pptx | ||
| 文件大小 | 52.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 11:20:33 | ||
图片预览











文档简介
(共31张PPT)
第4章 整式的加法与减法
4.2 合并同类项(1)
学习目标
1. 理解同类项的概念,能够认识同类项;
2. 会合并同类项,知道合并同类项所依据的运算律。
问题引入
上一节我们认识了整式,整式是不是可以像数一样进行运算呢
问题引入
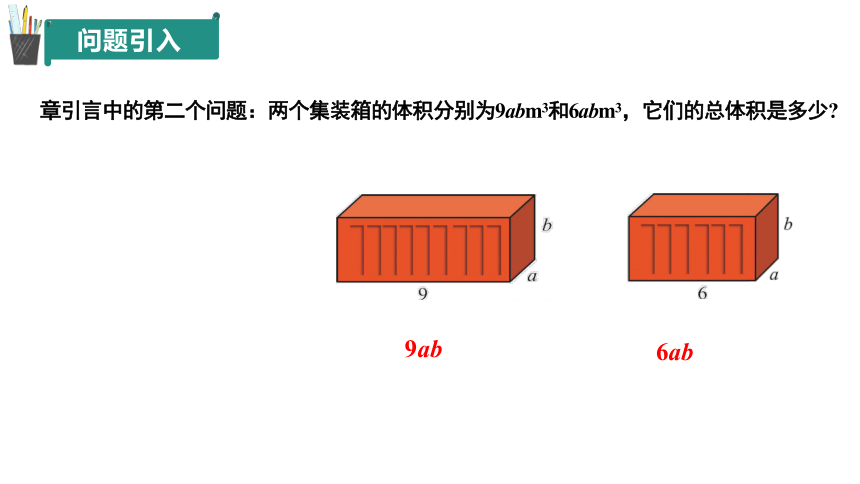
章引言中的第二个问题:两个集装箱的体积分别为9abm3和6abm3,它们的总体积是多少
9ab
6ab
问题引入
章引言中的第二个问题:两个集装箱的体积分别为9abm3和6abm3,它们的总体积是多少
总体积是两个集装箱体积之和,为(9ab+6ab)m3。
问题引入
章引言中的第二个问题:两个集装箱的体积分别为9abm3和6abm3,它们的总体积是多少
9ab
6ab
问题引入
章引言中的第二个问题:两个集装箱的体积分别为9abm3和6abm3,它们的总体积是多少
如图,可以把两个集装箱组合成一个长为15m,宽为a m,高为bm的新长方体,体积是15abm3。
9ab+6ab=15ab
9 ab+6 ab
思考与交流
(1)你能用乘法对加法的分配律说明为什么9ab+6ab=15ab吗
看作同一个数
=15 ab。
=(9+6) ab
(乘法对加法的分配律)
观察与发现
3x2+x2=(3+1) x2=4x2。
-5x2y+x2y=(-5+1)x2y=-5x2y。
(2)在多项式3x2-5x2y+x2+x2y中,哪些项可以合并成一项 它们有什么特征
(3)一般情况下,在多项式中,什么样的项可以合并成一项 怎样合并
概括与表达
像3x 与x ,-5x y与x y这样,所含字母相同,并且相同字母的指数也相同的项叫作同类项。
常数项都是同类项。
注意:同类项都是单项式。
新知巩固
① 3x与3mx是同类项。 ( )
② 2ab与-5ab是同类项。 ( )
③ 3x2y与-yx2是同类项。 ( )
④ 5ab2与-2ab2c是同类项。 ( )
⑤ 23与32是同类项。 ( )
⑥ x3与53是同类项。 ( )
判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
×
√
√
×
√
×
1.两相同:①字母相同;②相同字母指数相同。
2.两无关:与系数无关,与字母次序无关。
3.常数项都是同类项。
归纳与总结
同类项的判断方法:
两者必须同时满足,缺一不可。
概括与表达
把多项式中的同类项合并成一项,叫作合并同类项。
合并同类项时,把同类项的系数相加,所得的和作为系数,字母与字母的指数不变。
合并同类项法则
例题讲解
(1) 3x2+2x2; (2)-x2y-6x2y;
解:(1)3x2+2x2=(3+2)x2=5x2。
例1 合并下列各式中的同类项:
(2)-x2y-6x2y=(-1-6)x2y=-7x2y。
例题讲解
(3)2mn-5mn+10mn; (4)-3a2b+a2b+2a2b。
例1 合并下列各式中的同类项:
(4)-3a2b+a2b+2a2b=(-3+1+2)a2b=0。
(3)2mn-5mn+10mn=(2-5+10))mn=7mn。
归纳与总结
合并同类项的注意点:
一相加: 系数相加 (新系数为原来各系数的和。系数相加时要带上项的符号);
两不变:字母和字母指数不变 (原来的字母和字母的指数照抄)。
新知巩固
1. 判断下列计算是否正确,并说明理由。
(1) 3a+2b=5ab; (2) 5y2-3y2=2;
(3) 7ab-7ba=0; (4) 3x2+4x2=7x4。
2y2
7x2
新知巩固
2. 合并下列各式中的同类项:
(1) 3x-5x; (2) -xy+xy; (3)-a b-a b。
解:(1) 3x-5x=(3-5)x=-2x。
(2) -xy+xy=(-+)xy=0。
(3)-a b-a b=(-1-)a b=-a b。
新知巩固
3. 下列各式中的两项是否为同类项 如果是,请合并。
(1) a +b ; (2) a b+ba ; (3)-3a b +2a b 。
解:(1)不是。
(2) 是,a b+ba =(+)a b=a b。
(3) 不是。
拓展与提升
例2 已知关于x,y的单项式(5-m)x5yn与单项式-3y4是同类项,求m+n的值。
∴=5且5-m≠0,n=4,
解得m=±5且m≠5,n=4,
∴ m=-5,n=4,
∴ m+n=-5+4=-1。
解:∵单项式(5-m)x5yn与单项式-3y4是同类项,
1.同类项的概念。
2.合并同类项的概念和法则。
1.(2024·四川内江·中考真题)下列单项式中,的同类项是( )
A. B. C. D.
课堂检测
基础过关
A
2.(2024·江苏常州·中考真题)计算的结果是( )
A.2 B. C. D.
B
课堂检测
基础过关
3.(2023·四川宜宾·中考真题)下列计算正确的是( )
A.
B.
C.
D.
B
4.(2024·河南·中考真题)请写出的一个同类项: 。
课堂检测
基础过关
5.(2024·广东东莞·三模)已知单项式与是同类项,则的值为 。
m(答案不唯一)
课堂检测
基础过关
6.指出下列各组中的两项是不是同类项,若不是,请说明理由。
(1)与;(2)与0;(3)与;
(4)与; (5)与.
解:(1)(2)(5)都符合同类项的定义,都是同类项;
(3)与虽然所含的字母相同,但相同字母的指数都不相同,
所以它们不是同类项;
(4)与所含的字母不相同,故它们不是同类项.
课堂检测
基础过关
7.合并同类项:
(1);(2)。
解:(1)
;
(2);
。
课堂检测
能力提升
1.(2024·内蒙古包头·一模)下列各项中,能与合并的是( )
A. B. C. D.
C
2.下列各选项的两项中,属于同类项的是( )
A. 62与x2 B. 4ab与4abc C. 0.2x2y与0.2xy2 D. nm与-mn
D
课堂检测
能力提升
3.(2024·甘肃武威·三模)下列计算中正确的是( )
A.
B.
C.
D.
B
4.(2024·广东·二模)若,则______。
课堂检测
能力提升
4
5. 若7axb2与-a3by的和为单项式,则yx= 。
8
6. 化简:a-2a+3a-4a+5a-6a+…+99a-100a= 。
-50a
课堂检测
能力提升
7.合并同类项:
(1); (2) 。
解:(1);
(2)。
课堂检测
能力提升
8.(2023·广东清远·一模)已知关于的多项式化简后是单项式,其结果(关于的单项式)的系数为4,求的值。
解:关于的多项式的化简结果是单项式,
∴与是同类项,
,解得.
∵关于的多项式化简后是单项式,其结果(关于的单项式)的系数为4,
∴,
原式。
第4章 整式的加法与减法
4.2 合并同类项(1)
学习目标
1. 理解同类项的概念,能够认识同类项;
2. 会合并同类项,知道合并同类项所依据的运算律。
问题引入
上一节我们认识了整式,整式是不是可以像数一样进行运算呢
问题引入
章引言中的第二个问题:两个集装箱的体积分别为9abm3和6abm3,它们的总体积是多少
9ab
6ab
问题引入
章引言中的第二个问题:两个集装箱的体积分别为9abm3和6abm3,它们的总体积是多少
总体积是两个集装箱体积之和,为(9ab+6ab)m3。
问题引入
章引言中的第二个问题:两个集装箱的体积分别为9abm3和6abm3,它们的总体积是多少
9ab
6ab
问题引入
章引言中的第二个问题:两个集装箱的体积分别为9abm3和6abm3,它们的总体积是多少
如图,可以把两个集装箱组合成一个长为15m,宽为a m,高为bm的新长方体,体积是15abm3。
9ab+6ab=15ab
9 ab+6 ab
思考与交流
(1)你能用乘法对加法的分配律说明为什么9ab+6ab=15ab吗
看作同一个数
=15 ab。
=(9+6) ab
(乘法对加法的分配律)
观察与发现
3x2+x2=(3+1) x2=4x2。
-5x2y+x2y=(-5+1)x2y=-5x2y。
(2)在多项式3x2-5x2y+x2+x2y中,哪些项可以合并成一项 它们有什么特征
(3)一般情况下,在多项式中,什么样的项可以合并成一项 怎样合并
概括与表达
像3x 与x ,-5x y与x y这样,所含字母相同,并且相同字母的指数也相同的项叫作同类项。
常数项都是同类项。
注意:同类项都是单项式。
新知巩固
① 3x与3mx是同类项。 ( )
② 2ab与-5ab是同类项。 ( )
③ 3x2y与-yx2是同类项。 ( )
④ 5ab2与-2ab2c是同类项。 ( )
⑤ 23与32是同类项。 ( )
⑥ x3与53是同类项。 ( )
判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
×
√
√
×
√
×
1.两相同:①字母相同;②相同字母指数相同。
2.两无关:与系数无关,与字母次序无关。
3.常数项都是同类项。
归纳与总结
同类项的判断方法:
两者必须同时满足,缺一不可。
概括与表达
把多项式中的同类项合并成一项,叫作合并同类项。
合并同类项时,把同类项的系数相加,所得的和作为系数,字母与字母的指数不变。
合并同类项法则
例题讲解
(1) 3x2+2x2; (2)-x2y-6x2y;
解:(1)3x2+2x2=(3+2)x2=5x2。
例1 合并下列各式中的同类项:
(2)-x2y-6x2y=(-1-6)x2y=-7x2y。
例题讲解
(3)2mn-5mn+10mn; (4)-3a2b+a2b+2a2b。
例1 合并下列各式中的同类项:
(4)-3a2b+a2b+2a2b=(-3+1+2)a2b=0。
(3)2mn-5mn+10mn=(2-5+10))mn=7mn。
归纳与总结
合并同类项的注意点:
一相加: 系数相加 (新系数为原来各系数的和。系数相加时要带上项的符号);
两不变:字母和字母指数不变 (原来的字母和字母的指数照抄)。
新知巩固
1. 判断下列计算是否正确,并说明理由。
(1) 3a+2b=5ab; (2) 5y2-3y2=2;
(3) 7ab-7ba=0; (4) 3x2+4x2=7x4。
2y2
7x2
新知巩固
2. 合并下列各式中的同类项:
(1) 3x-5x; (2) -xy+xy; (3)-a b-a b。
解:(1) 3x-5x=(3-5)x=-2x。
(2) -xy+xy=(-+)xy=0。
(3)-a b-a b=(-1-)a b=-a b。
新知巩固
3. 下列各式中的两项是否为同类项 如果是,请合并。
(1) a +b ; (2) a b+ba ; (3)-3a b +2a b 。
解:(1)不是。
(2) 是,a b+ba =(+)a b=a b。
(3) 不是。
拓展与提升
例2 已知关于x,y的单项式(5-m)x5yn与单项式-3y4是同类项,求m+n的值。
∴=5且5-m≠0,n=4,
解得m=±5且m≠5,n=4,
∴ m=-5,n=4,
∴ m+n=-5+4=-1。
解:∵单项式(5-m)x5yn与单项式-3y4是同类项,
1.同类项的概念。
2.合并同类项的概念和法则。
1.(2024·四川内江·中考真题)下列单项式中,的同类项是( )
A. B. C. D.
课堂检测
基础过关
A
2.(2024·江苏常州·中考真题)计算的结果是( )
A.2 B. C. D.
B
课堂检测
基础过关
3.(2023·四川宜宾·中考真题)下列计算正确的是( )
A.
B.
C.
D.
B
4.(2024·河南·中考真题)请写出的一个同类项: 。
课堂检测
基础过关
5.(2024·广东东莞·三模)已知单项式与是同类项,则的值为 。
m(答案不唯一)
课堂检测
基础过关
6.指出下列各组中的两项是不是同类项,若不是,请说明理由。
(1)与;(2)与0;(3)与;
(4)与; (5)与.
解:(1)(2)(5)都符合同类项的定义,都是同类项;
(3)与虽然所含的字母相同,但相同字母的指数都不相同,
所以它们不是同类项;
(4)与所含的字母不相同,故它们不是同类项.
课堂检测
基础过关
7.合并同类项:
(1);(2)。
解:(1)
;
(2);
。
课堂检测
能力提升
1.(2024·内蒙古包头·一模)下列各项中,能与合并的是( )
A. B. C. D.
C
2.下列各选项的两项中,属于同类项的是( )
A. 62与x2 B. 4ab与4abc C. 0.2x2y与0.2xy2 D. nm与-mn
D
课堂检测
能力提升
3.(2024·甘肃武威·三模)下列计算中正确的是( )
A.
B.
C.
D.
B
4.(2024·广东·二模)若,则______。
课堂检测
能力提升
4
5. 若7axb2与-a3by的和为单项式,则yx= 。
8
6. 化简:a-2a+3a-4a+5a-6a+…+99a-100a= 。
-50a
课堂检测
能力提升
7.合并同类项:
(1); (2) 。
解:(1);
(2)。
课堂检测
能力提升
8.(2023·广东清远·一模)已知关于的多项式化简后是单项式,其结果(关于的单项式)的系数为4,求的值。
解:关于的多项式的化简结果是单项式,
∴与是同类项,
,解得.
∵关于的多项式化简后是单项式,其结果(关于的单项式)的系数为4,
∴,
原式。
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
