4.2合并同类项(第2课时) 课件(共33张ppt)
文档属性
| 名称 | 4.2合并同类项(第2课时) 课件(共33张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 50.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 14:39:35 | ||
图片预览











文档简介
(共33张PPT)
第4章 整式的加法与减法
4.2 合并同类项(2)
学习目标
1. 通过合并同类项,进一步巩固合并同类项法则;
2. 会先合并同类项再求值,体会合并同类项在代数式求值计算中的作用。
问题引入
上一节学习了合并同类项,我们一起来回忆一下同类项的概念以及合并同类项法则。
知识回顾
同类项的定义:所含 ,并且 的 也相同的项,叫做同类项。常数项都是_______。
字母相同
相同字母
指数
同类项
合并同类项法则:_______相加,作为结果的系数,字母和字母的指数______。
系数
不变
合并同类项用到了什么运算律?
分配律:a(b+c)=ab+ac
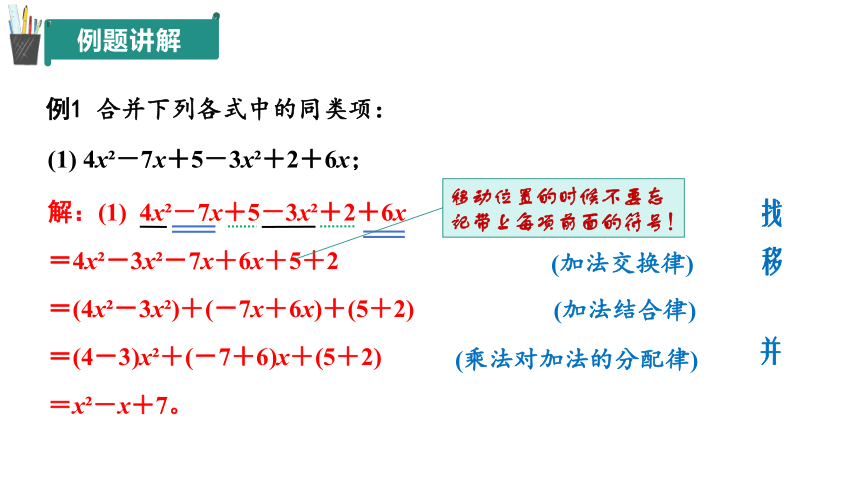
例题讲解
解:(1) 4x -7x+5-3x +2+6x
=4x -3x -7x+6x+5+2
=(4x -3x )+(-7x+6x)+(5+2)
=(4-3)x +(-7+6)x+(5+2)
=x -x+7。
例1 合并下列各式中的同类项:
(1) 4x -7x+5-3x +2+6x;
(加法交换律)
(加法结合律)
(乘法对加法的分配律)
找
移
移动位置的时候不要忘记带上每项前面的符号!
并
(2) 3a +9b +2ab-5a -5b
=3a -5a +9b -9b +2ab
=(3-5)a +(9-9)b +2ab
=-2a +2ab。
例题讲解
例1 合并下列各式中的同类项:
(2) 3a +9b +2ab-5a -5b 。
若两个同类项的系数互为相反数,则合并的结果为0。
归纳与总结
合并同类项的一般步骤:
(1)“找”:根据同类项的定义找出同类项,通常在同类项下面做相同的标记(如画线);
(2)“移”:利用加法交换律和结合律移动某些项的位置,移动位置时。要连同项的符号一起移动;
(3)“并”:根据“一相加,两不变”的法则合并同类项。
新知巩固
合并下列各式中的同类项:
(1) 3x-4y-2x+y; (2) x2-2xy-4x2 +6xy;
(3) 4a2b-5ab2-a2b+5ab2; (4) x3-x2+x3-x2+x。
例题讲解
解: 2x y-2xy +5x y+xy -4x y
=2x y+5x y-4x y-2xy +xy
=3x y-xy 。
当x=3,y=-2时,
原式=3×()2×(-2)-×(-2)
=--
=-2。
例2 当x=,y=-2时,求多项式2x y-2xy +5x y+xy -4x y的值。
在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算。
新知巩固
1. 先化简,再求值:3y2-6y+1-y2+2y-4,其中y=-2。
解: 3y2-6y+1-y2+2y-4
=3y2-y2-6y+2y+1-4
=2y2-4y-3。
当y=-2时,
原式=2×(-2)2-4×(-2)-3
=8+8-3
=13。
新知巩固
2. 已知(x-3)2+=0,求3x2y-2xy2+2xy-3x2y-3xy+5xy2的值。
解:∵(x-3)2+=0,
∴x-3=0,且y+ =0,即x=3,y=-,
3x2y-2xy2+2xy-3x2y-3xy+5xy2
=3x2y-3x2y-2xy2+5xy2+2xy-3xy
=3xy2-xy,
当x=3,y=- 时,
原式=3×3×(- )2-3×(- )=1+1=2。
例3 类比合并同类项,将下列式子进行化简:
(1) 3(a+b)+2(a+b)-4(a+b);
拓展与提升
解:(1) 方法一:
3(a+b)+2(a+b)-4(a+b)
=a+b。
方法二:
原式=3m+2m-4m=m,
设m=a+b,
即:原式=a+b。
化繁为简
整体思想
例3 类比合并同类项,将下列式子进行化简:
(2) 3(a+b) -2(a-b)-4(a+b) +2(a-b)。
拓展与提升
解:(2) 方法一:
3(a+b) -2(a-b)-4(a+b) +2(a-b)
=-(a+b) 。
方法二:
原式=3m2-2n-4m2+2n
=-m2,
设m=a+b,n=a-b,
即:原式=-(a+b) 。
拓展与提升
例4 已知关于x,y的多项式mx3+3nxy2+2x3-xy+y合并后不含三次项,求2m+3n的值。
解: mx3+3nxy2+2x3-xy+y
=(m+2)x3+3nxy2-xy+y,
∵合并后不含三次项,
∴m+2=0,3n=0,
所以m=-2,n=0,
所以2m+3n=2×(-2)+3×0=-4。
1. 求代数式5(x-2y)-3(x-2y)+8(x-2y)-4(x-2y)的值,其中x=y= 。
解:设x-2y=a,
原式=5a-3a+8a-4a=6a,
当x=y=时,
a=x-2y
=-2× ,
原式=6a= 6×(- = 1。
新知巩固
拓展与提升
2. 若多项式的值与x的取值无关,求的值;
解:
=,
∵原式的值与x的值无关,
∴,,
∴,,
∴
1.合并同类项的一般步骤:找、移、并。
2.多项式的化简求值。
课堂检测
基础过关
1.下列计算正确的是( )
A. B.
C. D.
A
课堂检测
基础过关
2.将多项式2x2-5x+x2+4x-3x2合并同类项后所得的结果是( )
A.二次二项式 B.二次三项式
C.一次二项式 D.单项式
D
课堂检测
基础过关
3.-5x2+3x-1+2x2+4x+9=__________________。
-3x2+7x+8
4.关于x的多项式ax-2bx合并同类项后的值为0,则a、b满足的条件是_______________。
a-2b=0
5.多项式中,不含项,则= 。
2
课堂检测
基础过关
6. 化简下列多项式:
(1)3a2-2a-a2+5a; (2)p2+5pq-8-7p2+2pq;
解:(1)原式=3a2-a2-2a+5a
=(3-1)a2+(-2+5)a
=2a2+3a。
(2)原式=p2-7p2+5pq+2pq-8
=(1-7)p2+(5+2)pq-8
=-6p2+7pq-8。
课堂检测
基础过关
7. 先化简,再求值:
(1)7x2-3x2-2x-2x2+5+6x,其中x=-2;
解:(1) 原式=2x2+4x+5,
当x=-2时,
原式=2×(-2)2+4×(-2)+5
=5。
课堂检测
基础过关
7. 先化简,再求值:
(2)5a-26+3b-4a-1,其中a=-1,b=2;
解:(2) 原式=a+3b-27,
当a=-1,b=2时,
原式=-1+6-27
=-22。
课堂检测
基础过关
8. 已知 a3+xb8-y与3a4b6是同类项,求3y3-4x3y-4y3+2x3y的值。
解:∵ a3+xb8-y与3a4b6是同类项,
∴3+x=4,8-y=6,即x=1,y=2.
3y3-4x3y-4y3+2x3y
=-y3-2x3y,
把x=1,y=2代入得,
原式=-23-2×13×2=-8-4=-12。
课堂检测
能力提升
1.(2024七年级上·全国·专题练习)下列合并同类项正确的是( )
; ; ;
;;;; .
A. B. C. D.
B
课堂检测
能力提升
2.已知多项式-的值与x无关,= 。
-8
3.若多项式与的和不含项,则 。
3
课堂检测
能力提升
4.如图中阴影部分的面积为 。(结果保留)
课堂检测
基础过关
5.合并同类项:
(1)4x2-8x+5-3x2+6x-2;
解:(1)原式=(4x2-3x2)+(-8x+6x)+(5-2)
=(4-3)x2+(-8+6)x+(5-2)
=x2-2x+3。
课堂检测
基础过关
解:(2)原式=(11x2-x2)+(4x-4x)-(1+5)
=10x2-6。
5.合并同类项:
(2)11x2+4x-1-x2-4x-5。
课堂检测
能力提升
6.先化简,再求值:
0.5a2b- ab2+0.5ba2+ b2a- a2b,其中a=-5,b=-3。
解:原式= a2b+ ab2。
当a=-5,b=-3时,
原式=×(-5)2×(-3)+×(-5)×(-3)2
=-15-15
=-30。
课堂检测
能力提升
7.把和各看成一个整体,对下列各式进行化简:
(1) ;
解:(1)
。
课堂检测
能力提升
7.把和各看成一个整体,对下列各式进行化简:
(2)。
解:(2)
课堂检测
能力提升
8.若关于x、y的多项式不含二次项,求的值;
解:
,
∵多项式不含二次项,
∴,,
∴,,
∴。
第4章 整式的加法与减法
4.2 合并同类项(2)
学习目标
1. 通过合并同类项,进一步巩固合并同类项法则;
2. 会先合并同类项再求值,体会合并同类项在代数式求值计算中的作用。
问题引入
上一节学习了合并同类项,我们一起来回忆一下同类项的概念以及合并同类项法则。
知识回顾
同类项的定义:所含 ,并且 的 也相同的项,叫做同类项。常数项都是_______。
字母相同
相同字母
指数
同类项
合并同类项法则:_______相加,作为结果的系数,字母和字母的指数______。
系数
不变
合并同类项用到了什么运算律?
分配律:a(b+c)=ab+ac
例题讲解
解:(1) 4x -7x+5-3x +2+6x
=4x -3x -7x+6x+5+2
=(4x -3x )+(-7x+6x)+(5+2)
=(4-3)x +(-7+6)x+(5+2)
=x -x+7。
例1 合并下列各式中的同类项:
(1) 4x -7x+5-3x +2+6x;
(加法交换律)
(加法结合律)
(乘法对加法的分配律)
找
移
移动位置的时候不要忘记带上每项前面的符号!
并
(2) 3a +9b +2ab-5a -5b
=3a -5a +9b -9b +2ab
=(3-5)a +(9-9)b +2ab
=-2a +2ab。
例题讲解
例1 合并下列各式中的同类项:
(2) 3a +9b +2ab-5a -5b 。
若两个同类项的系数互为相反数,则合并的结果为0。
归纳与总结
合并同类项的一般步骤:
(1)“找”:根据同类项的定义找出同类项,通常在同类项下面做相同的标记(如画线);
(2)“移”:利用加法交换律和结合律移动某些项的位置,移动位置时。要连同项的符号一起移动;
(3)“并”:根据“一相加,两不变”的法则合并同类项。
新知巩固
合并下列各式中的同类项:
(1) 3x-4y-2x+y; (2) x2-2xy-4x2 +6xy;
(3) 4a2b-5ab2-a2b+5ab2; (4) x3-x2+x3-x2+x。
例题讲解
解: 2x y-2xy +5x y+xy -4x y
=2x y+5x y-4x y-2xy +xy
=3x y-xy 。
当x=3,y=-2时,
原式=3×()2×(-2)-×(-2)
=--
=-2。
例2 当x=,y=-2时,求多项式2x y-2xy +5x y+xy -4x y的值。
在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算。
新知巩固
1. 先化简,再求值:3y2-6y+1-y2+2y-4,其中y=-2。
解: 3y2-6y+1-y2+2y-4
=3y2-y2-6y+2y+1-4
=2y2-4y-3。
当y=-2时,
原式=2×(-2)2-4×(-2)-3
=8+8-3
=13。
新知巩固
2. 已知(x-3)2+=0,求3x2y-2xy2+2xy-3x2y-3xy+5xy2的值。
解:∵(x-3)2+=0,
∴x-3=0,且y+ =0,即x=3,y=-,
3x2y-2xy2+2xy-3x2y-3xy+5xy2
=3x2y-3x2y-2xy2+5xy2+2xy-3xy
=3xy2-xy,
当x=3,y=- 时,
原式=3×3×(- )2-3×(- )=1+1=2。
例3 类比合并同类项,将下列式子进行化简:
(1) 3(a+b)+2(a+b)-4(a+b);
拓展与提升
解:(1) 方法一:
3(a+b)+2(a+b)-4(a+b)
=a+b。
方法二:
原式=3m+2m-4m=m,
设m=a+b,
即:原式=a+b。
化繁为简
整体思想
例3 类比合并同类项,将下列式子进行化简:
(2) 3(a+b) -2(a-b)-4(a+b) +2(a-b)。
拓展与提升
解:(2) 方法一:
3(a+b) -2(a-b)-4(a+b) +2(a-b)
=-(a+b) 。
方法二:
原式=3m2-2n-4m2+2n
=-m2,
设m=a+b,n=a-b,
即:原式=-(a+b) 。
拓展与提升
例4 已知关于x,y的多项式mx3+3nxy2+2x3-xy+y合并后不含三次项,求2m+3n的值。
解: mx3+3nxy2+2x3-xy+y
=(m+2)x3+3nxy2-xy+y,
∵合并后不含三次项,
∴m+2=0,3n=0,
所以m=-2,n=0,
所以2m+3n=2×(-2)+3×0=-4。
1. 求代数式5(x-2y)-3(x-2y)+8(x-2y)-4(x-2y)的值,其中x=y= 。
解:设x-2y=a,
原式=5a-3a+8a-4a=6a,
当x=y=时,
a=x-2y
=-2× ,
原式=6a= 6×(- = 1。
新知巩固
拓展与提升
2. 若多项式的值与x的取值无关,求的值;
解:
=,
∵原式的值与x的值无关,
∴,,
∴,,
∴
1.合并同类项的一般步骤:找、移、并。
2.多项式的化简求值。
课堂检测
基础过关
1.下列计算正确的是( )
A. B.
C. D.
A
课堂检测
基础过关
2.将多项式2x2-5x+x2+4x-3x2合并同类项后所得的结果是( )
A.二次二项式 B.二次三项式
C.一次二项式 D.单项式
D
课堂检测
基础过关
3.-5x2+3x-1+2x2+4x+9=__________________。
-3x2+7x+8
4.关于x的多项式ax-2bx合并同类项后的值为0,则a、b满足的条件是_______________。
a-2b=0
5.多项式中,不含项,则= 。
2
课堂检测
基础过关
6. 化简下列多项式:
(1)3a2-2a-a2+5a; (2)p2+5pq-8-7p2+2pq;
解:(1)原式=3a2-a2-2a+5a
=(3-1)a2+(-2+5)a
=2a2+3a。
(2)原式=p2-7p2+5pq+2pq-8
=(1-7)p2+(5+2)pq-8
=-6p2+7pq-8。
课堂检测
基础过关
7. 先化简,再求值:
(1)7x2-3x2-2x-2x2+5+6x,其中x=-2;
解:(1) 原式=2x2+4x+5,
当x=-2时,
原式=2×(-2)2+4×(-2)+5
=5。
课堂检测
基础过关
7. 先化简,再求值:
(2)5a-26+3b-4a-1,其中a=-1,b=2;
解:(2) 原式=a+3b-27,
当a=-1,b=2时,
原式=-1+6-27
=-22。
课堂检测
基础过关
8. 已知 a3+xb8-y与3a4b6是同类项,求3y3-4x3y-4y3+2x3y的值。
解:∵ a3+xb8-y与3a4b6是同类项,
∴3+x=4,8-y=6,即x=1,y=2.
3y3-4x3y-4y3+2x3y
=-y3-2x3y,
把x=1,y=2代入得,
原式=-23-2×13×2=-8-4=-12。
课堂检测
能力提升
1.(2024七年级上·全国·专题练习)下列合并同类项正确的是( )
; ; ;
;;;; .
A. B. C. D.
B
课堂检测
能力提升
2.已知多项式-的值与x无关,= 。
-8
3.若多项式与的和不含项,则 。
3
课堂检测
能力提升
4.如图中阴影部分的面积为 。(结果保留)
课堂检测
基础过关
5.合并同类项:
(1)4x2-8x+5-3x2+6x-2;
解:(1)原式=(4x2-3x2)+(-8x+6x)+(5-2)
=(4-3)x2+(-8+6)x+(5-2)
=x2-2x+3。
课堂检测
基础过关
解:(2)原式=(11x2-x2)+(4x-4x)-(1+5)
=10x2-6。
5.合并同类项:
(2)11x2+4x-1-x2-4x-5。
课堂检测
能力提升
6.先化简,再求值:
0.5a2b- ab2+0.5ba2+ b2a- a2b,其中a=-5,b=-3。
解:原式= a2b+ ab2。
当a=-5,b=-3时,
原式=×(-5)2×(-3)+×(-5)×(-3)2
=-15-15
=-30。
课堂检测
能力提升
7.把和各看成一个整体,对下列各式进行化简:
(1) ;
解:(1)
。
课堂检测
能力提升
7.把和各看成一个整体,对下列各式进行化简:
(2)。
解:(2)
课堂检测
能力提升
8.若关于x、y的多项式不含二次项,求的值;
解:
,
∵多项式不含二次项,
∴,,
∴,,
∴。
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
