4.3.2用一元一次方程解决问题——行程问题(同步课件)-七年级数学上册同步精品课堂(苏科版2024)
文档属性
| 名称 | 4.3.2用一元一次方程解决问题——行程问题(同步课件)-七年级数学上册同步精品课堂(苏科版2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 35.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 11:25:43 | ||
图片预览







文档简介
(共26张PPT)
4.3.2 用一元一次方程解决问题——行程问题
第4章 一元一次方程
教学目标
01
掌握与行程问题有关的基本公式,进一步用一元一次方程解决相遇问题、追及问题、相背问题等,初步理解“单位1”的概念
问 题 目 录
销售问题
??问题
行程问题
……
Q1:小明从家步行到学校大约需要20min,走的路程为1200m,求小明步行的速度。
小明步行的速度==60m/min
Q2:(1)行程问题中的基本量是什么?
(2)这些基本量之间的关系是什么?
路程=速度×时间
速度、路程、时间
01
情境引入
Part1:乌龟与兔子相遇的故事
乌龟的速度是10m/min,
兔子的速度是590m/min,
两家相距15000m,
龟兔同时出发,
请问多久以后他们会在路上遇到呢?
啦啦啦~
跑啊跑~
01
情境引入
解:设x分钟后它们在路上相遇,
相遇
根据题意得:590x+10x=15000,
590x
10x
10m/min
590m/min
15000m
解得:x=25,
答:乌龟和兔子经过了25分钟后可以相遇。
01
情境引入
Part2:乌龟与兔子追及的故事
乌龟的速度是10m/min,兔子的速度是590m/min,
乌龟出发2个小时后兔子再出发,请问多久以后兔子能追上乌龟?
看我追上你~
让我先走2个小时
01
情境引入
设x分钟后兔子追上乌龟,
追及
590x
10x
590m/min
10m/min
根据题意得:590x-10x=1200,
解:兔子出发时与乌龟的距离为:10×120=1200(m),
1200m
01
情境引入
解得:x=,答:兔子再经过了分钟追上乌龟。
02
590x+10x=15000
相遇问题
02
知识精讲
相遇
590x
10x
15000m
相遇问题的等量关系:两者的路程之和=两者间的距离。
追及问题
02
知识精讲
追及
590x
10x
1200m
590x-10x=1200
追及问题的等量关系:两者的路程之差=两者间的距离。
例1、甲、乙两站相距365km,一列慢车从甲地开往乙地,每小时行驶65km,慢车行驶1h后,另有一列快车从乙站开往甲站,每小时行驶85km,快车行驶几小时后与慢车相遇?
【分析】相遇问题:两者的路程之和=两者间的距离
03
典例精析
适当画图更清楚哦~
365km
甲
乙
慢车
快车
65km/h
85km/h
相遇
65(x+1)
85x
解:设快车行驶x小时后与慢车相遇,则慢车行驶(x+1)小时,
根据题意得:65(x+1)+85x=365,
解得:x=2,
答:快车行驶2小时后与慢车相遇。
365km
甲
乙
慢车
快车
65km/h
85km/h
03
典例精析
例2、一队学生去校外进行军事野营训练,他们以5km/h的速度行进,走了18min的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14km/h的速度按原路追上去,通讯员需多少时间可以追上学生队伍?
【分析】追及问题:两者的路程之差=两者间的距离
03
典例精析
注意:
单位要统一,可提前单位换算:18min=h=h
追及
5km/h
14km/h
通讯员
学生
km
03
典例精析
设通讯员需x小时可以追上学生队伍,
14x
5x
解:通讯员出发时与乌龟的距离为:5×=(km),
根据题意得:14x-5x=,
解得:x=,答:通讯员需小时可以追上学生队伍。
例3、甲从A地到B地需4h,乙从B地到A地需10h。
(1)若两人同时相向而行,几小时可以相遇?
(2)若两人同时同向而行,甲几小时可以追到乙?
【分析】(1)相遇问题:两者的路程之和=两者间的距离
(2)追及问题:两者的路程之差=两者间的距离
未知速度和总路程该如何列式呢?
若是知道总路程,甲、乙的速度就可以分别表示出来了
03
典例精析
不妨设总路程为单位1
03
典例精析
什么是单位1?
单位1:
泛指一个完整的量,比如一段路程、一项工程、一箱苹果、一本书、一段时间等,再赋予它们自然数1的特性。
03
典例精析
【分析】若总路程为“1”,则甲的速度为,乙的速度为,
解:(1)设x小时可以相遇,
根据题意得:x+x=1,
解得:x=,
答:若两人同时相向而行,小时可以相遇;
03
典例精析
(2)设家x小时可以追到乙,
根据题意得:x-x=1,
解得:x=,
答:若两人同时同向而行,甲小时可以追到乙。
例4、甲、乙两站相距480km,一列慢车从甲站开出,每小时行90km,一列快车从乙站开出,每小时行140km。
(1)慢车先开出1h,快车再开,两车相向而行,问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600km?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600km?
【分析】(1)相遇问题:两者的路程之和=两者间的距离
03
典例精析
解:(1)设快车开出x小时后两车相遇,
根据题意得:90(x+1)+140x=480,
解得:x=,答:快车开出小时后两车相遇。
【分析】
(2)相遇问题的变形——相背问题
03
典例精析
例4、甲、乙两站相距480km,一列慢车从甲站开出,每小时行90km,一列快车从乙站开出,每小时行140km。
(1)慢车先开出1h,快车再开,两车相向而行,问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600km?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600km?
相背问题也要画图哦~
480km
甲
乙
←慢车
快车→
90km/h
140km/h
600km
(2)设相背而行x小时后两车相距600km,
480km
甲
乙
←慢车
快车→
90km/h
140km/h
600km
90x
140x
03
典例精析
根据题意得:90x+480+140x=600,
解得:x=,
答:相背而行小时后两车相距600km。
【分析】
(3)追及问题的变形——追击未追上问题
03
典例精析
例4、甲、乙两站相距480km,一列慢车从甲站开出,每小时行90km,一列快车从乙站开出,每小时行140km。
(1)慢车先开出1h,快车再开,两车相向而行,问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600km?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600km?
480km
甲
乙
慢车→
快车→
90km/h
140km/h
追击未追上问题也要画图哦~
(3)设x小时后两车相距600km,
480km
甲
乙
慢车→
快车→
90km/h
140km/h
600km
03
典例精析
140x
90x
根据题意得:480+140x=90x+600,
解得:x=,答:小时后两车相距600km。
90x+480+140x=600
480km
甲
乙
←慢车
快车→
90km/h
140km/h
600km
90x
140x
相背问题
03
典例精析
相背问题的等量关系:
两者的路程之和+两者的初距离=两者的终距离。
480+140x=90x+600,即140x-90x=600-480
追击未追上问题
480km
甲
乙
慢车→
快车→
600km
140x
90x
03
典例精析
追击未追上问题的等量关系:
两者的路程之差=|两者的终距离-两者的初距离|。
课后总结
路程问题的几种情形:
相遇问题的等量关系:两者的路程之和=两者间的距离。
追及问题的等量关系:两者的路程之差=两者间的距离。
相背问题的等量关系:两者的路程之和+两者的初距离=两者的终距离。
追击未追上问题的等量关系:两者的路程之差=|两者的终距离-两者的初距离|。
单位1:
泛指一个完整的量,比如一段路程、一项工程、一箱苹果、一本书、一段时间等,再赋予它们自然数1的特性。
4.3.2 用一元一次方程解决问题——行程问题
第4章 一元一次方程
教学目标
01
掌握与行程问题有关的基本公式,进一步用一元一次方程解决相遇问题、追及问题、相背问题等,初步理解“单位1”的概念
问 题 目 录
销售问题
??问题
行程问题
……
Q1:小明从家步行到学校大约需要20min,走的路程为1200m,求小明步行的速度。
小明步行的速度==60m/min
Q2:(1)行程问题中的基本量是什么?
(2)这些基本量之间的关系是什么?
路程=速度×时间
速度、路程、时间
01
情境引入
Part1:乌龟与兔子相遇的故事
乌龟的速度是10m/min,
兔子的速度是590m/min,
两家相距15000m,
龟兔同时出发,
请问多久以后他们会在路上遇到呢?
啦啦啦~
跑啊跑~
01
情境引入
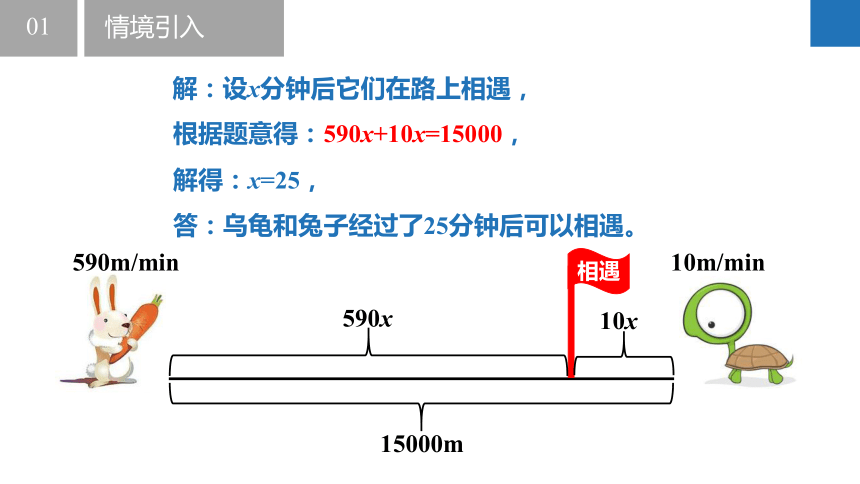
解:设x分钟后它们在路上相遇,
相遇
根据题意得:590x+10x=15000,
590x
10x
10m/min
590m/min
15000m
解得:x=25,
答:乌龟和兔子经过了25分钟后可以相遇。
01
情境引入
Part2:乌龟与兔子追及的故事
乌龟的速度是10m/min,兔子的速度是590m/min,
乌龟出发2个小时后兔子再出发,请问多久以后兔子能追上乌龟?
看我追上你~
让我先走2个小时
01
情境引入
设x分钟后兔子追上乌龟,
追及
590x
10x
590m/min
10m/min
根据题意得:590x-10x=1200,
解:兔子出发时与乌龟的距离为:10×120=1200(m),
1200m
01
情境引入
解得:x=,答:兔子再经过了分钟追上乌龟。
02
590x+10x=15000
相遇问题
02
知识精讲
相遇
590x
10x
15000m
相遇问题的等量关系:两者的路程之和=两者间的距离。
追及问题
02
知识精讲
追及
590x
10x
1200m
590x-10x=1200
追及问题的等量关系:两者的路程之差=两者间的距离。
例1、甲、乙两站相距365km,一列慢车从甲地开往乙地,每小时行驶65km,慢车行驶1h后,另有一列快车从乙站开往甲站,每小时行驶85km,快车行驶几小时后与慢车相遇?
【分析】相遇问题:两者的路程之和=两者间的距离
03
典例精析
适当画图更清楚哦~
365km
甲
乙
慢车
快车
65km/h
85km/h
相遇
65(x+1)
85x
解:设快车行驶x小时后与慢车相遇,则慢车行驶(x+1)小时,
根据题意得:65(x+1)+85x=365,
解得:x=2,
答:快车行驶2小时后与慢车相遇。
365km
甲
乙
慢车
快车
65km/h
85km/h
03
典例精析
例2、一队学生去校外进行军事野营训练,他们以5km/h的速度行进,走了18min的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14km/h的速度按原路追上去,通讯员需多少时间可以追上学生队伍?
【分析】追及问题:两者的路程之差=两者间的距离
03
典例精析
注意:
单位要统一,可提前单位换算:18min=h=h
追及
5km/h
14km/h
通讯员
学生
km
03
典例精析
设通讯员需x小时可以追上学生队伍,
14x
5x
解:通讯员出发时与乌龟的距离为:5×=(km),
根据题意得:14x-5x=,
解得:x=,答:通讯员需小时可以追上学生队伍。
例3、甲从A地到B地需4h,乙从B地到A地需10h。
(1)若两人同时相向而行,几小时可以相遇?
(2)若两人同时同向而行,甲几小时可以追到乙?
【分析】(1)相遇问题:两者的路程之和=两者间的距离
(2)追及问题:两者的路程之差=两者间的距离
未知速度和总路程该如何列式呢?
若是知道总路程,甲、乙的速度就可以分别表示出来了
03
典例精析
不妨设总路程为单位1
03
典例精析
什么是单位1?
单位1:
泛指一个完整的量,比如一段路程、一项工程、一箱苹果、一本书、一段时间等,再赋予它们自然数1的特性。
03
典例精析
【分析】若总路程为“1”,则甲的速度为,乙的速度为,
解:(1)设x小时可以相遇,
根据题意得:x+x=1,
解得:x=,
答:若两人同时相向而行,小时可以相遇;
03
典例精析
(2)设家x小时可以追到乙,
根据题意得:x-x=1,
解得:x=,
答:若两人同时同向而行,甲小时可以追到乙。
例4、甲、乙两站相距480km,一列慢车从甲站开出,每小时行90km,一列快车从乙站开出,每小时行140km。
(1)慢车先开出1h,快车再开,两车相向而行,问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600km?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600km?
【分析】(1)相遇问题:两者的路程之和=两者间的距离
03
典例精析
解:(1)设快车开出x小时后两车相遇,
根据题意得:90(x+1)+140x=480,
解得:x=,答:快车开出小时后两车相遇。
【分析】
(2)相遇问题的变形——相背问题
03
典例精析
例4、甲、乙两站相距480km,一列慢车从甲站开出,每小时行90km,一列快车从乙站开出,每小时行140km。
(1)慢车先开出1h,快车再开,两车相向而行,问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600km?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600km?
相背问题也要画图哦~
480km
甲
乙
←慢车
快车→
90km/h
140km/h
600km
(2)设相背而行x小时后两车相距600km,
480km
甲
乙
←慢车
快车→
90km/h
140km/h
600km
90x
140x
03
典例精析
根据题意得:90x+480+140x=600,
解得:x=,
答:相背而行小时后两车相距600km。
【分析】
(3)追及问题的变形——追击未追上问题
03
典例精析
例4、甲、乙两站相距480km,一列慢车从甲站开出,每小时行90km,一列快车从乙站开出,每小时行140km。
(1)慢车先开出1h,快车再开,两车相向而行,问快车开出多少小时后两车相遇?
(2)两车同时开出,相背而行多少小时后两车相距600km?
(3)两车同时开出,慢车在快车后面同向而行,多少小时后快车与慢车相距600km?
480km
甲
乙
慢车→
快车→
90km/h
140km/h
追击未追上问题也要画图哦~
(3)设x小时后两车相距600km,
480km
甲
乙
慢车→
快车→
90km/h
140km/h
600km
03
典例精析
140x
90x
根据题意得:480+140x=90x+600,
解得:x=,答:小时后两车相距600km。
90x+480+140x=600
480km
甲
乙
←慢车
快车→
90km/h
140km/h
600km
90x
140x
相背问题
03
典例精析
相背问题的等量关系:
两者的路程之和+两者的初距离=两者的终距离。
480+140x=90x+600,即140x-90x=600-480
追击未追上问题
480km
甲
乙
慢车→
快车→
600km
140x
90x
03
典例精析
追击未追上问题的等量关系:
两者的路程之差=|两者的终距离-两者的初距离|。
课后总结
路程问题的几种情形:
相遇问题的等量关系:两者的路程之和=两者间的距离。
追及问题的等量关系:两者的路程之差=两者间的距离。
相背问题的等量关系:两者的路程之和+两者的初距离=两者的终距离。
追击未追上问题的等量关系:两者的路程之差=|两者的终距离-两者的初距离|。
单位1:
泛指一个完整的量,比如一段路程、一项工程、一箱苹果、一本书、一段时间等,再赋予它们自然数1的特性。
同课章节目录
