5.1函数与它的表示法(第1课时)(同步课件)-九年级数学下册同步精品课堂(青岛版)
文档属性
| 名称 | 5.1函数与它的表示法(第1课时)(同步课件)-九年级数学下册同步精品课堂(青岛版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 11:27:22 | ||
图片预览







文档简介
(共23张PPT)
5.1 函数与它的表示方法(第1课时)
主讲:
青岛版数学九年级下册
第1章 对函数的再探索
目录
02
复习导入
03
观察与思考
04
合作探究
05
课堂练习
06
课堂小结
01
课程目标
课程目标
1.回顾函数的概念,掌握函数的三种表示方法:解析法、列表法、图象法。
2.能够恰当地运用函数的三种表示方法解决一些实际问题,初步培养将实际问题转化为数学问题的能力。
我们在七年级和八年级的课程中都学到了函数的相关知识,请同学们仔细回忆,回答下列问题。
问题一:什么是函数?
问题二:什么是函数的表达式?
问题三:我们之前学过哪个函数?表达式是什么?
在同一个变化过程中,有两个变量x和y,如果对于变量x的每一个确定的值,都能随之确定一个y值,就把y叫做x的函数,其中x叫自变量。
如果一个变量与另一个变量之间的函数关系可以用一个数学式子表示出来,我们就把这个数学式子叫做该函数的表达式。
一次函数 y=kx+b (k≠0)
复习导入
观察与思考
在现实生活中,函数关系是处处存在的,那表示函数关系的方法通常有哪些呢?我们一起看下面三个实际问题,观察并回答问题。
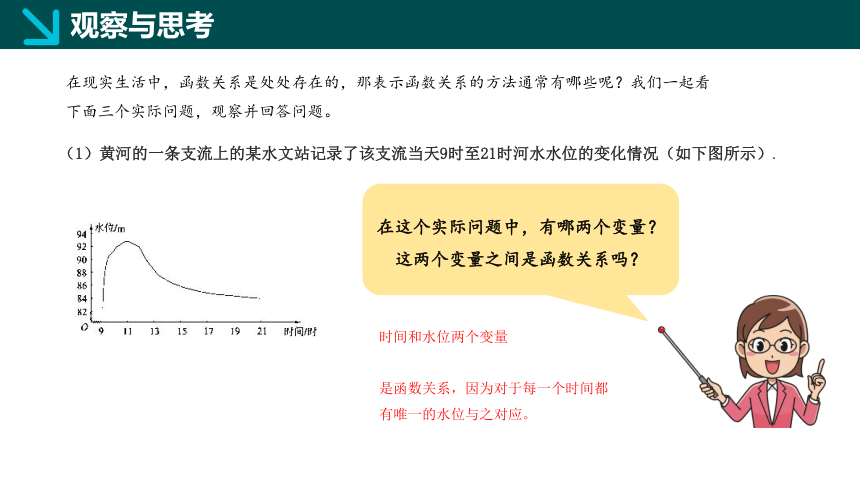
(1)黄河的一条支流上的某水文站记录了该支流当天9时至21时河水水位的变化情况(如下图所示).
时间和水位两个变量
是函数关系,因为对于每一个时间都有唯一的水位与之对应。
在这个实际问题中,有哪两个变量?这两个变量之间是函数关系吗?
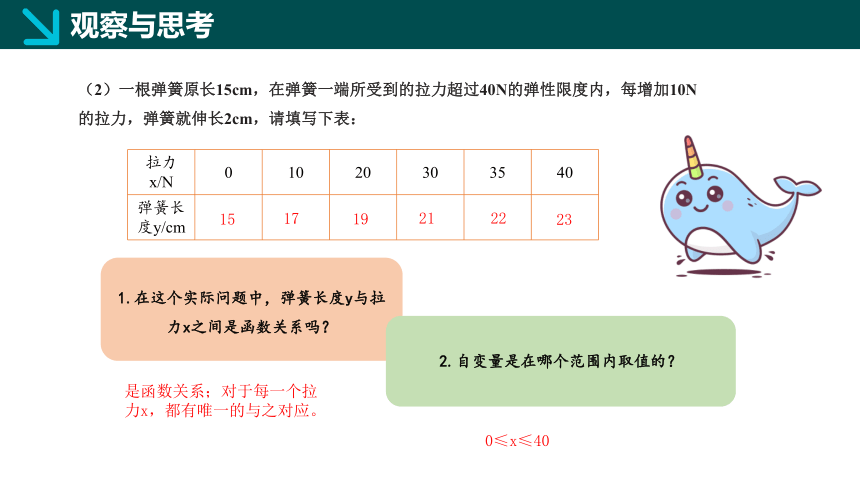
(2)一根弹簧原长15cm,在弹簧一端所受到的拉力超过40N的弹性限度内,每增加10N的拉力,弹簧就伸长2cm,请填写下表:
拉力x/N 0 10 20 30 35 40
弹簧长度y/cm
0≤x≤40
观察与思考
1.在这个实际问题中,弹簧长度y与拉力x之间是函数关系吗?
2.自变量是在哪个范围内取值的?
是函数关系;对于每一个拉力x,都有唯一的与之对应。
15
17
21
22
23
19
它的图象是以A(0,15)和B(40,23)为端点的一条线段.
由此可设函数的表达式为y = kx + 15(k是常数,0≤x≤40)
将x = 40,y = 23代入上式,得
23 = 40k + 15,
解得,k=
所以这个函数的表达式为
是一次函数
观察与思考
刚刚同学们已经确定y与x是函数关系,那么这个函数是一次函数吗?如果是,写出y与x的表达式。
不要忘记自变量的取值范围哦
用描点法画出函数图像。
根据函数的表达式和自变量可以取值的范围,列出下面的表格:
以时间t为横轴、高度h为纵轴画出直角坐标系(根据该问题的实际背景,横轴和纵轴选取不同的单位长度),然后以上表中的每一个有序实数对(t,h)为坐标,在直角坐标系中描出相应的各点,用一条平滑的曲线按自左向右的顺序顺次连接它们,便得函数y=490-4.9t2(0≤t≤10)的图象.它是一段曲线。
观察与思考
(3)物体从490m的高度处自由下落,物体距地面的高度h(m)与物体下落的时间 t(s)之间的关系满足表达式 h = 490-4.9t2
0≤t≤10
观察与思考
在这个实际问题中,物体距地面的高度h与物体下落的时间t之间是函数关系吗?
自变量是在哪个范围内取值的?
是函数关系
合作探究
上述(1)(2)(3)中,分别是用哪种方法表示两个变量之间的函数关系的?
(1)
(2)
(3)
图像法
列表法
解析法
合作探究
方法 优点 不足
图像法 直观,能够形象地反映出当自变量的值变化时函数值的变化趋势 不能准确地由
已知自变量的值求出函数值
列表法 已知表中给出的部分自变量的值 时,可以不通过计算直接查出对应的函数值 只能表示出自变量的
有限个离散值及其函数值
解析法 全面、准确、方便,对于自变量在 可以取值的范围内任取一个确定的值,都可以通过表达式计算求出它的函数 值 并不是每一个函数都可写出它的表达式,
例如上面问题(1)中的函数关系就无法用一个表达式表
以上3种表示方法各有哪些优点和不足?同学们小组讨论。
课堂练习
【例题1】一辆汽车在一段行驶过程中,速度v随行驶时间t变化的情况如图所示.
(1)在这个问题中,速度v与行驶时间t之间的函数关系是用哪种方法表示的?
(2)这个过程中汽车共行驶了多少分钟?在哪个时间段内,汽车行驶速度最大?最大速度是多少?
(3)在哪个时间段内汽车的行驶速度逐渐增加?在哪个时间段内行驶速度逐渐减少?在哪个时间段内汽车按匀速运动行驶?按匀速运动行驶时,速度是多少?
(4)根据图象,填写下表:
t/min 0 20 40 60 80 100 120
v/(km/h)
课堂练习
【解答】
(1)由题意可得,
在这个问题中,速度v与行驶时间t之间的函数关系是用图象法表示的;
(2)由图象可得,
这个过程中汽车共行驶了120分钟,在40~80这个时间段内,汽车行驶速度最大,最大速度是90km/h;
(3)由图象可得,
在0~10和20~40这两个时间段内汽车的行驶速度逐渐增加,在80~100这个时间段内行驶速度逐渐减少,在10~20、40~80和100~120这三个时间段内汽车按匀速运动行驶,按匀速运动行驶时,速度是60km/h,90km/h,60km/h;
(4)由图象可得,
当t=0时,v=0;当t=20时,v=60;当t=40时,v=90;当t=60时,v=90;当t=80时,v=90;当t=100时,v=60;
当t=120时,v=60;
故答案为:0,60,90,90,90,60,60.
t/min 0 20 40 60 80 100 120
v/(km/h) 0 60 90 90 90 60 60
课堂练习
【例题2】如图,正三角形ABC内接于圆O,设圆的半径为r.你能写出图中阴影部分的面积S与半径r之间的函数关系吗?你认为用哪种方法表示它们之间的函数关系比较方便?
课堂练习
【分析】
【解答】
所以利用解析式表示它们之间的函数关系比较方便.
课堂练习
【巩固练习1】
(2024春 市南区期末)我国首辆火星车正式被命名为:“祝融”,为应对极限温度环境,火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率K(W/m K)与温度T(℃)的关系如表,下列选项描述不正确的是( )
温度T(℃) 100 150 200 250
导热率K(W/m K) 0.15 0.2 0.25 0.3
A.在这个变化过程中,自变量是温度,因变量是导热率
B.在一定温度范围内,温度越高,该材料导热率越高
C.当温度为350℃时,该材料导热率为0.35W/m K
D.温度每升高增高10℃该材料导热率增加0.01W/m K
变式训练
课堂练习
【分析】
A.根据自变量和因变量的定义判断即可;
B.根据表格中数据的变化情况判断即可;
CD.根据数据变化规律判断即可.
【解答】
解:在这个变化过程中,导热率随着温度的变化而变化,即自变量是温度,因变量是导热率,
∴A正确,不符合题意;
根据表格可知,在一定温度范围内,温度越高,该材料导热率越高,
∴B正确,不符合题意;
根据表格可知,温度每升高50℃,导热率增加0.05W/m K,
∴当温度为350℃时,该材料导热率为0.4W/m K,
∴C不正确,符合题意;
∵温度每升高50℃,导热率增加0.05W/m K,
∴温度每升高增高10℃该材料导热率增加0.01W/m K,
∴D正确,不符合题意.
故选:C.
课堂练习
【巩固练习2】
(2024春 市北区期中)赵先生手中有一张记录他从出生到24周岁期间的身高情况表(如下):
年龄x/岁 0 3 6 9 12 15 18 21 24
身高h/cm 48 100 130 140 150 158 165 170 170.4
下列说法错误的是( )
A.赵先生的身高从0岁到3岁增长最快
B.赵先生的身高增长速度总体上先快后慢
C.赵先生的身高在21岁以后基本不长了
D.赵先生期待自己的身高在27岁时自然生长到180cm,这个愿望能够实现
变式训练
课堂练习
【分析】利用统计表给出的数据,逐项分析得出答案即可.
【解答】解:A、赵先生的身高从0岁到3岁增长最快,故不符合题意;
B、赵先生的身高增长速度总体上先快后慢,故不符合题意;
C、赵先生的身高在21岁以后基本不长了,故不符合题意;
D、赵先生的身高在21岁以后基本不长了,长到180cm的这个愿望不能够实现,故符合题意.
故选:D.
课堂练习
【巩固练习3】
(2024春 即墨区期中)一汽车油箱里有油40L,在行驶过程中,每小时耗油2.5L,回答下列问题:
(1)汽车行驶1h后油箱里还有油 L,汽车行驶6h后油箱里还有油 L;
(2)这一变化过程中共有 个变量,其中 是变
量, 是常量;
(3)设汽车行驶的时间为x h,油箱里剩下的油为Q L,请用含x的式子表示Q;
(4)这辆汽车最多能行驶多少小时?
变式训练
课堂练习
【分析】(1)根据邮箱里剩下的油量=油箱里原有的油量﹣耗油的油量,即可求出答案.
(2)根据题中的三个数量:油箱里原有的油量、油箱里剩下的油量和行驶的时间,直接判断出变化的量就是变量和不变的量就是常量.
(3)根据邮箱里的剩下的油量=油箱里原有的油量﹣每小时耗油的油量×时间,直接用字母表达即可.
(4)根据题意,使剩下的油量Q=0,即可用表达式求出结果.
【解答】解:(1)40﹣2.5=37.5(L),
40﹣2.5×6=25(L),
故答案为:37.5;25.
(2)这一变化过程中共有2个变量,
其中邮箱里剩下的油量和行驶的时间是变量,
每小时耗油的油量是常量,
故答案为:2;邮箱里剩下的油量和行驶的时间;每小时耗油的油量.
(3)Q=40﹣2.5x.
(4)40﹣2.5x=0,
解得x=16.
答:这辆汽车最多能行驶16小时.
课堂小结
1.函数的3种表示方法:解析法、列表法、图像法
2.三种方法的优缺点
主讲:
青岛版数学九年级下册
感谢聆听
5.1 函数与它的表示方法(第1课时)
主讲:
青岛版数学九年级下册
第1章 对函数的再探索
目录
02
复习导入
03
观察与思考
04
合作探究
05
课堂练习
06
课堂小结
01
课程目标
课程目标
1.回顾函数的概念,掌握函数的三种表示方法:解析法、列表法、图象法。
2.能够恰当地运用函数的三种表示方法解决一些实际问题,初步培养将实际问题转化为数学问题的能力。
我们在七年级和八年级的课程中都学到了函数的相关知识,请同学们仔细回忆,回答下列问题。
问题一:什么是函数?
问题二:什么是函数的表达式?
问题三:我们之前学过哪个函数?表达式是什么?
在同一个变化过程中,有两个变量x和y,如果对于变量x的每一个确定的值,都能随之确定一个y值,就把y叫做x的函数,其中x叫自变量。
如果一个变量与另一个变量之间的函数关系可以用一个数学式子表示出来,我们就把这个数学式子叫做该函数的表达式。
一次函数 y=kx+b (k≠0)
复习导入
观察与思考
在现实生活中,函数关系是处处存在的,那表示函数关系的方法通常有哪些呢?我们一起看下面三个实际问题,观察并回答问题。
(1)黄河的一条支流上的某水文站记录了该支流当天9时至21时河水水位的变化情况(如下图所示).
时间和水位两个变量
是函数关系,因为对于每一个时间都有唯一的水位与之对应。
在这个实际问题中,有哪两个变量?这两个变量之间是函数关系吗?
(2)一根弹簧原长15cm,在弹簧一端所受到的拉力超过40N的弹性限度内,每增加10N的拉力,弹簧就伸长2cm,请填写下表:
拉力x/N 0 10 20 30 35 40
弹簧长度y/cm
0≤x≤40
观察与思考
1.在这个实际问题中,弹簧长度y与拉力x之间是函数关系吗?
2.自变量是在哪个范围内取值的?
是函数关系;对于每一个拉力x,都有唯一的与之对应。
15
17
21
22
23
19
它的图象是以A(0,15)和B(40,23)为端点的一条线段.
由此可设函数的表达式为y = kx + 15(k是常数,0≤x≤40)
将x = 40,y = 23代入上式,得
23 = 40k + 15,
解得,k=
所以这个函数的表达式为
是一次函数
观察与思考
刚刚同学们已经确定y与x是函数关系,那么这个函数是一次函数吗?如果是,写出y与x的表达式。
不要忘记自变量的取值范围哦
用描点法画出函数图像。
根据函数的表达式和自变量可以取值的范围,列出下面的表格:
以时间t为横轴、高度h为纵轴画出直角坐标系(根据该问题的实际背景,横轴和纵轴选取不同的单位长度),然后以上表中的每一个有序实数对(t,h)为坐标,在直角坐标系中描出相应的各点,用一条平滑的曲线按自左向右的顺序顺次连接它们,便得函数y=490-4.9t2(0≤t≤10)的图象.它是一段曲线。
观察与思考
(3)物体从490m的高度处自由下落,物体距地面的高度h(m)与物体下落的时间 t(s)之间的关系满足表达式 h = 490-4.9t2
0≤t≤10
观察与思考
在这个实际问题中,物体距地面的高度h与物体下落的时间t之间是函数关系吗?
自变量是在哪个范围内取值的?
是函数关系
合作探究
上述(1)(2)(3)中,分别是用哪种方法表示两个变量之间的函数关系的?
(1)
(2)
(3)
图像法
列表法
解析法
合作探究
方法 优点 不足
图像法 直观,能够形象地反映出当自变量的值变化时函数值的变化趋势 不能准确地由
已知自变量的值求出函数值
列表法 已知表中给出的部分自变量的值 时,可以不通过计算直接查出对应的函数值 只能表示出自变量的
有限个离散值及其函数值
解析法 全面、准确、方便,对于自变量在 可以取值的范围内任取一个确定的值,都可以通过表达式计算求出它的函数 值 并不是每一个函数都可写出它的表达式,
例如上面问题(1)中的函数关系就无法用一个表达式表
以上3种表示方法各有哪些优点和不足?同学们小组讨论。
课堂练习
【例题1】一辆汽车在一段行驶过程中,速度v随行驶时间t变化的情况如图所示.
(1)在这个问题中,速度v与行驶时间t之间的函数关系是用哪种方法表示的?
(2)这个过程中汽车共行驶了多少分钟?在哪个时间段内,汽车行驶速度最大?最大速度是多少?
(3)在哪个时间段内汽车的行驶速度逐渐增加?在哪个时间段内行驶速度逐渐减少?在哪个时间段内汽车按匀速运动行驶?按匀速运动行驶时,速度是多少?
(4)根据图象,填写下表:
t/min 0 20 40 60 80 100 120
v/(km/h)
课堂练习
【解答】
(1)由题意可得,
在这个问题中,速度v与行驶时间t之间的函数关系是用图象法表示的;
(2)由图象可得,
这个过程中汽车共行驶了120分钟,在40~80这个时间段内,汽车行驶速度最大,最大速度是90km/h;
(3)由图象可得,
在0~10和20~40这两个时间段内汽车的行驶速度逐渐增加,在80~100这个时间段内行驶速度逐渐减少,在10~20、40~80和100~120这三个时间段内汽车按匀速运动行驶,按匀速运动行驶时,速度是60km/h,90km/h,60km/h;
(4)由图象可得,
当t=0时,v=0;当t=20时,v=60;当t=40时,v=90;当t=60时,v=90;当t=80时,v=90;当t=100时,v=60;
当t=120时,v=60;
故答案为:0,60,90,90,90,60,60.
t/min 0 20 40 60 80 100 120
v/(km/h) 0 60 90 90 90 60 60
课堂练习
【例题2】如图,正三角形ABC内接于圆O,设圆的半径为r.你能写出图中阴影部分的面积S与半径r之间的函数关系吗?你认为用哪种方法表示它们之间的函数关系比较方便?
课堂练习
【分析】
【解答】
所以利用解析式表示它们之间的函数关系比较方便.
课堂练习
【巩固练习1】
(2024春 市南区期末)我国首辆火星车正式被命名为:“祝融”,为应对极限温度环境,火星车使用的是新型隔温材料——纳米气凝胶,该材料导热率K(W/m K)与温度T(℃)的关系如表,下列选项描述不正确的是( )
温度T(℃) 100 150 200 250
导热率K(W/m K) 0.15 0.2 0.25 0.3
A.在这个变化过程中,自变量是温度,因变量是导热率
B.在一定温度范围内,温度越高,该材料导热率越高
C.当温度为350℃时,该材料导热率为0.35W/m K
D.温度每升高增高10℃该材料导热率增加0.01W/m K
变式训练
课堂练习
【分析】
A.根据自变量和因变量的定义判断即可;
B.根据表格中数据的变化情况判断即可;
CD.根据数据变化规律判断即可.
【解答】
解:在这个变化过程中,导热率随着温度的变化而变化,即自变量是温度,因变量是导热率,
∴A正确,不符合题意;
根据表格可知,在一定温度范围内,温度越高,该材料导热率越高,
∴B正确,不符合题意;
根据表格可知,温度每升高50℃,导热率增加0.05W/m K,
∴当温度为350℃时,该材料导热率为0.4W/m K,
∴C不正确,符合题意;
∵温度每升高50℃,导热率增加0.05W/m K,
∴温度每升高增高10℃该材料导热率增加0.01W/m K,
∴D正确,不符合题意.
故选:C.
课堂练习
【巩固练习2】
(2024春 市北区期中)赵先生手中有一张记录他从出生到24周岁期间的身高情况表(如下):
年龄x/岁 0 3 6 9 12 15 18 21 24
身高h/cm 48 100 130 140 150 158 165 170 170.4
下列说法错误的是( )
A.赵先生的身高从0岁到3岁增长最快
B.赵先生的身高增长速度总体上先快后慢
C.赵先生的身高在21岁以后基本不长了
D.赵先生期待自己的身高在27岁时自然生长到180cm,这个愿望能够实现
变式训练
课堂练习
【分析】利用统计表给出的数据,逐项分析得出答案即可.
【解答】解:A、赵先生的身高从0岁到3岁增长最快,故不符合题意;
B、赵先生的身高增长速度总体上先快后慢,故不符合题意;
C、赵先生的身高在21岁以后基本不长了,故不符合题意;
D、赵先生的身高在21岁以后基本不长了,长到180cm的这个愿望不能够实现,故符合题意.
故选:D.
课堂练习
【巩固练习3】
(2024春 即墨区期中)一汽车油箱里有油40L,在行驶过程中,每小时耗油2.5L,回答下列问题:
(1)汽车行驶1h后油箱里还有油 L,汽车行驶6h后油箱里还有油 L;
(2)这一变化过程中共有 个变量,其中 是变
量, 是常量;
(3)设汽车行驶的时间为x h,油箱里剩下的油为Q L,请用含x的式子表示Q;
(4)这辆汽车最多能行驶多少小时?
变式训练
课堂练习
【分析】(1)根据邮箱里剩下的油量=油箱里原有的油量﹣耗油的油量,即可求出答案.
(2)根据题中的三个数量:油箱里原有的油量、油箱里剩下的油量和行驶的时间,直接判断出变化的量就是变量和不变的量就是常量.
(3)根据邮箱里的剩下的油量=油箱里原有的油量﹣每小时耗油的油量×时间,直接用字母表达即可.
(4)根据题意,使剩下的油量Q=0,即可用表达式求出结果.
【解答】解:(1)40﹣2.5=37.5(L),
40﹣2.5×6=25(L),
故答案为:37.5;25.
(2)这一变化过程中共有2个变量,
其中邮箱里剩下的油量和行驶的时间是变量,
每小时耗油的油量是常量,
故答案为:2;邮箱里剩下的油量和行驶的时间;每小时耗油的油量.
(3)Q=40﹣2.5x.
(4)40﹣2.5x=0,
解得x=16.
答:这辆汽车最多能行驶16小时.
课堂小结
1.函数的3种表示方法:解析法、列表法、图像法
2.三种方法的优缺点
主讲:
青岛版数学九年级下册
感谢聆听
