23.1平移变换(同步课件)-九年级数学下册同步精品课堂(北京版)
文档属性
| 名称 | 23.1平移变换(同步课件)-九年级数学下册同步精品课堂(北京版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 11:40:54 | ||
图片预览







文档简介
(共28张PPT)
23.1 平移变换
主讲:
京改版九年级下册
第23章 图形的变换
章节导入
仔细观察这些美丽的图案,你能根据其中的一部分绘制出整个图案吗?
在这一章中,我们将走进图形变换的天地,探索图形变换的规律
学习目标
目标
1
目标
2
1.通过具体实例认识图形的平移变换,探索它的基本性质.
目标
3
2.能按要求作出简单的平面图形平移后的图形.
3.要明确平面图形的平移变换,不少平面图案都可以看作是由其中的某一部分,沿着上下或左右的方向,平移若干次而成的。
自学指导
仔细阅读教材P2---P3。用3分钟的时间看谁又快又好地解决以下问题:
1.什么是平移?
2.平移后的图形有什么特点?
实践
探究新知
在滑梯过程中,小朋友身体各部分运动的方向相同吗?运动距离呢?
答:方向相同;
运动距离相同。
这些图形的运动过程与小朋友滑滑梯的运动过程,是否有共同点?若有是什么?
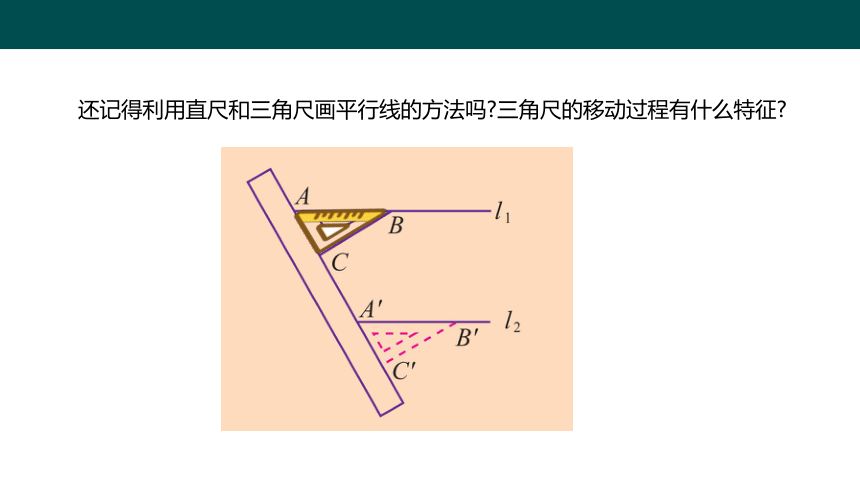
还记得利用直尺和三角尺画平行线的方法吗 三角尺的移动过程有什么特征
像这样,在平面内,将一个图形沿某个方向移动一定的距离,得到个新的图形,这样的图形运动称为平移变换,简称平移。
平移不改变图形的形状和大小。
知识要点
平移的定义
说一说
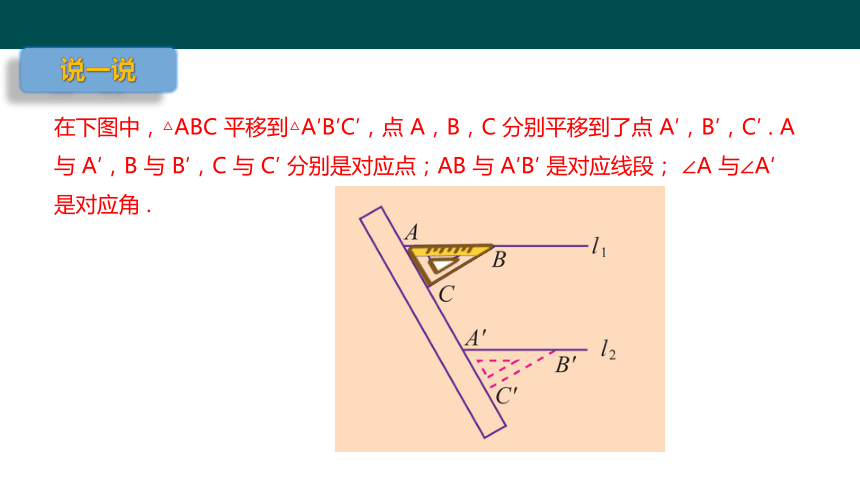
在下图中,△ABC 平移到△A′B′C′,点 A,B,C 分别平移到了点 A′,B′,C′ . A 与 A′,B 与 B′,C 与 C′ 分别是对应点;AB 与 A′B′ 是对应线段; ∠A 与∠A′ 是对应角 .
下面两个图形的变换各是什么变换?请说明理由。
做一做
答:平移变换;对称变换。
交流
1. 在下图中,对应线段、对应角之间有怎样的关系?
答:对应线段相等;对应角相等。
2. 在下图中,如果△ABC 沿着 PQ 方向移动到△A′B′C′ 的 位置,对应点所连的线段有怎样的关系?在图中,如果△ABC 沿着 MN 方向移动到△A″B″C″ 的位置呢?
经过平移,图形的对应线段相等且平行 ( 或在一条直线上 ) ;对应角相等;对应点所连的线段相等且平行 (或在同一条直线上 ).
知识要点
平移的性质
典型例题
例1 如图 ,平移△ABC,使点 A 移动到点 A′,作出平移后的△A′B′C′ .
分析:利用图形平移后对应点的特征,作出点 B,C 的对应点 B′,C′ .
如图,连接 AA′,过点 B 与点 C 分别作 AA′ 的平行线 l,l′,在l,l′ 上分别截取 BB′ = AA′,CC′ = AA′,则点 B′ 就是点 B 的对应点,点 C′ 就是点 C 的对应点 . 连接 A′B′,B′C′,C′A′,△A′B′C′ 就是△ABC 平移后的图形。
确定一个图形平移后的位置,需要什么条件?
交流
答:方向与距离。
例2 如图,将 N 状的图形按箭头所指的方向平移 3 cm,作出平移后的图形 .
典型例题
解:在图形上,找出关键的 4 个点,分别过这 4 个点按箭头所指的方向作
4 条长为 3 cm 的线段,将所作线段的另 4 个端点按原来的顺序连接,即可得到平移后的图形 .
实践
如图 ,在方格纸中,画出将图中的△ABC 向右平移 3 格后的△A′B′C′,然 后 再 画 出 将 △A′B′C′ 向 上 平 移 2 格 后的 △A″B″C″ . △A″B″C″ 是 否 可 以 看 成 是△ABC 经过一次平移后得到的呢?
实践
如图, 将 点 A( 2,3 ) 向左平移 4 个单位长度,得到点 A′,在图上标出这个点,并写出它的坐标;把点A 向下平移 3 个单位长度呢?把点 A 向右或向上平移呢?再找几个点,对它们进行平移,观察它们坐标的变化,你能从中发现什么规律?
A′
答:A′(-2,3);A 向下平移 3 个单位长度的点位置为(2,0).
在平面直角坐标系中,将点 ( x,y ) 向右 ( 或向左 ) 平移 a ( a > 0 )
个单位长度,可以得到对应点 ( x + a,y ) [或 ( x - a,y )] ;将点 ( x,y ) 向上 ( 或向下) 平移 b ( b > 0 ) 个单位长度,可以得到对应点 ( x,y + b ) [或 ( x,y - b ) ].
坐标的平移
例3 已知:如图 ,在梯形 ABCD 中,AD ∥ BC,对角线 AC,BD 交于点 O,AC = BD,且∠AOD = 60° .
求证:BC + AD = AC .
证明:过点 D 作 AC 的平行线,交 BC 的延长线于点 E,得四边形 ACED . 又∵ AD ∥ CE, ∴ 四边形 ACED 是平行四边形 .
∴ AC = DE,AD = CE .
又∵ AC = BD, ∴ BD = DE .
∵ DE ∥ AC,∠AOD = 60°,
∴ ∠BDE = 60° .
∴ △BDE 是等边三角形 .
∴ BE = DE = AC .
∵ BC + CE = AC,
∴ BC + AD = AC .
基础检测
1.下列图形中,哪个可以通过如图平移得到( )
2.如图,将△ABC沿BC方向平移到△DEF,若A,D之间的距离为2,CE=3,则BF等于( )
A.6 B.7 C.8 D.9
C
A. B. C. D.
B
3.如图,已知A,B的坐标分别为(1,2),(3,0),将△OAB沿x轴正方向平移,使B平移到点E,得到△DCE,若OE=4,则点C的坐标为( )。
A.(2,2) B.(3,2) C.(1,3) D.(1,4)
4.点A(3,4)向右平移2个单位长度,得到的点的坐标是( )。
A.(5,4) B.(3,6) C.(3,2) D.(1,4)
A
A
一展身手
如图,在边长为1的小正方形方格纸中,△ABC的顶点都在方格纸格点上.将△ABC使点A变换为点A',点B'、C'分别是B、C的对应点.
(1)请在图中画出平移后的△A'B'C';
(2)求△A'B'C'的面积.
解:(1)如图所示,△A'B'C'即为所求;
(2)△A'B'C'的面积.
挑战自我
如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
解:(1)结合所画图形可得:A1坐标为(4,7),点B1坐标为(1,2),C1坐标为(6,4).
(2)所画图形如下:
S△ABC=S矩形EBGF﹣S△ABE﹣S△GBC﹣S△AFC=255﹣3.
课堂小结
平移变换
1.平移的定义
2.平移的性质
3.与坐标有关的平移
主讲:
感谢聆听
京改版九年级下册
23.1 平移变换
主讲:
京改版九年级下册
第23章 图形的变换
章节导入
仔细观察这些美丽的图案,你能根据其中的一部分绘制出整个图案吗?
在这一章中,我们将走进图形变换的天地,探索图形变换的规律
学习目标
目标
1
目标
2
1.通过具体实例认识图形的平移变换,探索它的基本性质.
目标
3
2.能按要求作出简单的平面图形平移后的图形.
3.要明确平面图形的平移变换,不少平面图案都可以看作是由其中的某一部分,沿着上下或左右的方向,平移若干次而成的。
自学指导
仔细阅读教材P2---P3。用3分钟的时间看谁又快又好地解决以下问题:
1.什么是平移?
2.平移后的图形有什么特点?
实践
探究新知
在滑梯过程中,小朋友身体各部分运动的方向相同吗?运动距离呢?
答:方向相同;
运动距离相同。
这些图形的运动过程与小朋友滑滑梯的运动过程,是否有共同点?若有是什么?
还记得利用直尺和三角尺画平行线的方法吗 三角尺的移动过程有什么特征
像这样,在平面内,将一个图形沿某个方向移动一定的距离,得到个新的图形,这样的图形运动称为平移变换,简称平移。
平移不改变图形的形状和大小。
知识要点
平移的定义
说一说
在下图中,△ABC 平移到△A′B′C′,点 A,B,C 分别平移到了点 A′,B′,C′ . A 与 A′,B 与 B′,C 与 C′ 分别是对应点;AB 与 A′B′ 是对应线段; ∠A 与∠A′ 是对应角 .
下面两个图形的变换各是什么变换?请说明理由。
做一做
答:平移变换;对称变换。
交流
1. 在下图中,对应线段、对应角之间有怎样的关系?
答:对应线段相等;对应角相等。
2. 在下图中,如果△ABC 沿着 PQ 方向移动到△A′B′C′ 的 位置,对应点所连的线段有怎样的关系?在图中,如果△ABC 沿着 MN 方向移动到△A″B″C″ 的位置呢?
经过平移,图形的对应线段相等且平行 ( 或在一条直线上 ) ;对应角相等;对应点所连的线段相等且平行 (或在同一条直线上 ).
知识要点
平移的性质
典型例题
例1 如图 ,平移△ABC,使点 A 移动到点 A′,作出平移后的△A′B′C′ .
分析:利用图形平移后对应点的特征,作出点 B,C 的对应点 B′,C′ .
如图,连接 AA′,过点 B 与点 C 分别作 AA′ 的平行线 l,l′,在l,l′ 上分别截取 BB′ = AA′,CC′ = AA′,则点 B′ 就是点 B 的对应点,点 C′ 就是点 C 的对应点 . 连接 A′B′,B′C′,C′A′,△A′B′C′ 就是△ABC 平移后的图形。
确定一个图形平移后的位置,需要什么条件?
交流
答:方向与距离。
例2 如图,将 N 状的图形按箭头所指的方向平移 3 cm,作出平移后的图形 .
典型例题
解:在图形上,找出关键的 4 个点,分别过这 4 个点按箭头所指的方向作
4 条长为 3 cm 的线段,将所作线段的另 4 个端点按原来的顺序连接,即可得到平移后的图形 .
实践
如图 ,在方格纸中,画出将图中的△ABC 向右平移 3 格后的△A′B′C′,然 后 再 画 出 将 △A′B′C′ 向 上 平 移 2 格 后的 △A″B″C″ . △A″B″C″ 是 否 可 以 看 成 是△ABC 经过一次平移后得到的呢?
实践
如图, 将 点 A( 2,3 ) 向左平移 4 个单位长度,得到点 A′,在图上标出这个点,并写出它的坐标;把点A 向下平移 3 个单位长度呢?把点 A 向右或向上平移呢?再找几个点,对它们进行平移,观察它们坐标的变化,你能从中发现什么规律?
A′
答:A′(-2,3);A 向下平移 3 个单位长度的点位置为(2,0).
在平面直角坐标系中,将点 ( x,y ) 向右 ( 或向左 ) 平移 a ( a > 0 )
个单位长度,可以得到对应点 ( x + a,y ) [或 ( x - a,y )] ;将点 ( x,y ) 向上 ( 或向下) 平移 b ( b > 0 ) 个单位长度,可以得到对应点 ( x,y + b ) [或 ( x,y - b ) ].
坐标的平移
例3 已知:如图 ,在梯形 ABCD 中,AD ∥ BC,对角线 AC,BD 交于点 O,AC = BD,且∠AOD = 60° .
求证:BC + AD = AC .
证明:过点 D 作 AC 的平行线,交 BC 的延长线于点 E,得四边形 ACED . 又∵ AD ∥ CE, ∴ 四边形 ACED 是平行四边形 .
∴ AC = DE,AD = CE .
又∵ AC = BD, ∴ BD = DE .
∵ DE ∥ AC,∠AOD = 60°,
∴ ∠BDE = 60° .
∴ △BDE 是等边三角形 .
∴ BE = DE = AC .
∵ BC + CE = AC,
∴ BC + AD = AC .
基础检测
1.下列图形中,哪个可以通过如图平移得到( )
2.如图,将△ABC沿BC方向平移到△DEF,若A,D之间的距离为2,CE=3,则BF等于( )
A.6 B.7 C.8 D.9
C
A. B. C. D.
B
3.如图,已知A,B的坐标分别为(1,2),(3,0),将△OAB沿x轴正方向平移,使B平移到点E,得到△DCE,若OE=4,则点C的坐标为( )。
A.(2,2) B.(3,2) C.(1,3) D.(1,4)
4.点A(3,4)向右平移2个单位长度,得到的点的坐标是( )。
A.(5,4) B.(3,6) C.(3,2) D.(1,4)
A
A
一展身手
如图,在边长为1的小正方形方格纸中,△ABC的顶点都在方格纸格点上.将△ABC使点A变换为点A',点B'、C'分别是B、C的对应点.
(1)请在图中画出平移后的△A'B'C';
(2)求△A'B'C'的面积.
解:(1)如图所示,△A'B'C'即为所求;
(2)△A'B'C'的面积.
挑战自我
如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:(1)平移后的三个顶点坐标分别为:A1 ,B1 ,C1 ;
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
解:(1)结合所画图形可得:A1坐标为(4,7),点B1坐标为(1,2),C1坐标为(6,4).
(2)所画图形如下:
S△ABC=S矩形EBGF﹣S△ABE﹣S△GBC﹣S△AFC=255﹣3.
课堂小结
平移变换
1.平移的定义
2.平移的性质
3.与坐标有关的平移
主讲:
感谢聆听
京改版九年级下册
