26.1.1反比例函数(教学课件)-九年级数学下册同步教学精品课件(人教版)
文档属性
| 名称 | 26.1.1反比例函数(教学课件)-九年级数学下册同步教学精品课件(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
2 6 . 1 . 1 反比例函数
第二十六章 反比例函数
人教版·九年级·下册·第二十六章·反比例函数
学习目标
1
理解反比例函数的概念和意义,并会判断一个给定的函数是不是反比例函数;
2
能根据实际问题和已知条件用待定系数法求出反比例函数的解析式;理解反比例关系与反比例函数的区别与联系;
3
通过对反比例函数的研究和对一次函数(正比例函数)、二次函数的回顾,感受这三种函数之间的区别,体会数学中函数思想的应用;
知识回顾
函数
一次函数:
二次函数:
其他函数……
形如的函数
(正比例函数是特殊的一次函数)
函数是描述两个变量之间一一对应的数量关系的一个数学概念
反比例函数
形如的函数
?
新课探究
思考:下列问题中的变量间具有函数关系吗?如果有,请写出它们的解析式,并观察它们有什么共同特点?
问题1. 京沪线铁路全程为1463 km,某次列车的平均速度v (单位:km/h) 随此次列车的全程运行时间 t (单位:h) 的变化而变化;
解析:
函数解析式为:
速度会随着变小
两个变量和
时间变大
所以,这两个变量之间具有函数关系;
对于每一个确定的值, 都有唯一确定的值与其对应
解析:
函数解析式为:
长会随着变小
两个变量y和
宽变大
所以,这两个变量之间具有函数关系;
对于每一个确定的值, 都有唯一确定的值与其对应
问题2. 某住宅小区要种植一块面积为 1000 m2 的矩形草坪,草坪的长 (单位:m) 随宽 (单位:m)的变化而变化;
解析:
函数解析式为:
人均占有面积会随着变小
两个变量S和
人口变大
所以,这两个变量之间具有函数关系;
对于每一个确定的值, 都有唯一确定的值与其对应
问题3. 已知北京市的总面积为1.68×104 km2 ,人均占有面积 (km2/人) 随全市总人口 (单位:人) 的变化而变化.
小结:
问题1 得到的函数1:
问题2 得到的函数2:
问题3 得到的函数3:
请问以上三个函数有什么共同点?
分式的形式
分子上都是非零常数
新知讲解
一、反比例函数
1.概念:
一般地,形如 (为常数,) 的函数,叫做反比例函数 ,其中 是自变量, 是函数.
其中自变量的取值范围是:不等于0的一切实数(即)
称为比例系数
是分式中的分母,分母不为0
典例实践
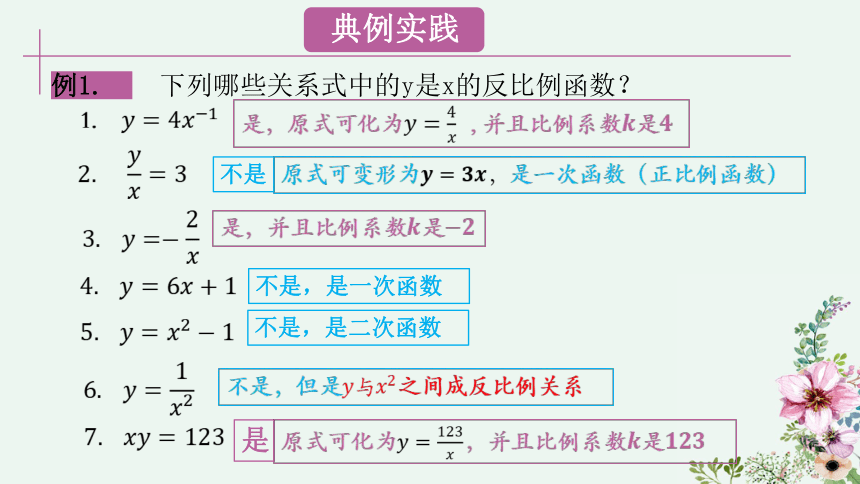
例1. 下列哪些关系式中的y是x的反比例函数?
1.
是,原式可化为, 并且比例系数是
不是
原式可变形为是一次函数(正比例函数)
是,并且比例系数是
不是,是一次函数
不是,是二次函数
不是,但是之间成反比例关系
是
原式可化为,并且比例系数是
新知讲解
2. 反比例函数解析式的几种形式:
典例小结
(1) ()
(2)
(3)
新知讲解
3. 反比例关系与反比例函数
典例小结
(1)反比例关系:
如果是常数,那么
与这两个变量成反比例关系,这里的可以表示多项式或者单项式;
如果 与 成反比例,则 (k 为常数,k≠0)
或者k 为常数,k≠0)
新知讲解
典例小结
(2)反比例关系与反比例函数的区别与联系:
两个变量成反比例关系,但不一定是反比例函数,但反比例函数 ()中的两个变量之间一定成反比例关系;
比如 与 成反比例,则 (k 为常数,k≠0)
此时并不是的反比例函数
反比例关系
反比例函数
典例实践
例2. 已知 与 成反比例,并且当时,
(1)写出关于的函数解析式;
(2)当时,求的值;
解
将中得
典例实践
例2. 已知 与 成反比例,并且当时,
(1)写出关于的函数解析式;
(2)当时,求的值;
(2)解
将 中得
中
得
例3. 已知 的反比例函数,并且当时,
(1)写出关于的函数解析式;
(2)当时,求的值;
解
将中得
(2)将 中
得
新知讲解
二、利用待定系数法求反比例函数的解析式
步骤:
①设(设出反比例函数解析式 () );
②代(将一组自变量与函数的对应值)代入解析式,
得到关于待定系数k的方程);
③解(解方程,求出待定系数k);
④写 (代入k,写出反比例函数解析式).
课堂练习
用函数解析式表示下列问题中变量间的对应关系,并判断是否是反比例函数;
(1)一个游泳池的容积为 1 800 m3,游泳池注满水所用时间 t(单位:h)
随注水速度 v(单位:m3/h)的变化而变化;
是反比例函数,其中
(2)某长方体的体积为 1 000 cm3,长方体的高 h(单位:cm)随底面积 S(单位:cm2)的变化而变化;
是反比例函数,其中
课堂练习
(3)一个物体重 100 N,物体对地面的压强 p(单位:Pa)随物体与地面的接触面积 S(单位:m2)的变化而变化.
P
(4)果果用完30元买练习本,买的练习本的本书y(单位:本)随练习本的价格x(单位:元)的变化而变化.
是反比例函数,其中
是反比例函数,其中
课堂练习
2. 已知反比例函数的解析式为 y = ,则 的取值范围是( )
课堂练习
3. 当为何值时,关于的反比例函数?
解关于的反比例函数
则
得
得
∴当 时,关于的反比例函数
课堂练习
拓展1. 当为何值时,关于的正比例函数?
解关于的正比例函数
则
得
得
∴当 时,关于的反比例函数
课堂练习
拓展2. 当为何值时,关于的二次函数?
解关于的二次函数
则
得
得
∴当 时,关于的二次函数
课堂小结
反比例函数
形如 (为常数,) 的函数,叫做反比例函数
概念
解析式的形式
(
待定系数法
①设:设反比例函数解析式为
(;
②代:将一对对应值代入解析式,
得到关于k的方程;
③解:解方程,求出k;
④写:代入k写出解析式
2 6 . 1 . 1 反比例函数
第二十六章 反比例函数
人教版·九年级·下册·第二十六章·反比例函数
学习目标
1
理解反比例函数的概念和意义,并会判断一个给定的函数是不是反比例函数;
2
能根据实际问题和已知条件用待定系数法求出反比例函数的解析式;理解反比例关系与反比例函数的区别与联系;
3
通过对反比例函数的研究和对一次函数(正比例函数)、二次函数的回顾,感受这三种函数之间的区别,体会数学中函数思想的应用;
知识回顾
函数
一次函数:
二次函数:
其他函数……
形如的函数
(正比例函数是特殊的一次函数)
函数是描述两个变量之间一一对应的数量关系的一个数学概念
反比例函数
形如的函数
?
新课探究
思考:下列问题中的变量间具有函数关系吗?如果有,请写出它们的解析式,并观察它们有什么共同特点?
问题1. 京沪线铁路全程为1463 km,某次列车的平均速度v (单位:km/h) 随此次列车的全程运行时间 t (单位:h) 的变化而变化;
解析:
函数解析式为:
速度会随着变小
两个变量和
时间变大
所以,这两个变量之间具有函数关系;
对于每一个确定的值, 都有唯一确定的值与其对应
解析:
函数解析式为:
长会随着变小
两个变量y和
宽变大
所以,这两个变量之间具有函数关系;
对于每一个确定的值, 都有唯一确定的值与其对应
问题2. 某住宅小区要种植一块面积为 1000 m2 的矩形草坪,草坪的长 (单位:m) 随宽 (单位:m)的变化而变化;
解析:
函数解析式为:
人均占有面积会随着变小
两个变量S和
人口变大
所以,这两个变量之间具有函数关系;
对于每一个确定的值, 都有唯一确定的值与其对应
问题3. 已知北京市的总面积为1.68×104 km2 ,人均占有面积 (km2/人) 随全市总人口 (单位:人) 的变化而变化.
小结:
问题1 得到的函数1:
问题2 得到的函数2:
问题3 得到的函数3:
请问以上三个函数有什么共同点?
分式的形式
分子上都是非零常数
新知讲解
一、反比例函数
1.概念:
一般地,形如 (为常数,) 的函数,叫做反比例函数 ,其中 是自变量, 是函数.
其中自变量的取值范围是:不等于0的一切实数(即)
称为比例系数
是分式中的分母,分母不为0
典例实践
例1. 下列哪些关系式中的y是x的反比例函数?
1.
是,原式可化为, 并且比例系数是
不是
原式可变形为是一次函数(正比例函数)
是,并且比例系数是
不是,是一次函数
不是,是二次函数
不是,但是之间成反比例关系
是
原式可化为,并且比例系数是
新知讲解
2. 反比例函数解析式的几种形式:
典例小结
(1) ()
(2)
(3)
新知讲解
3. 反比例关系与反比例函数
典例小结
(1)反比例关系:
如果是常数,那么
与这两个变量成反比例关系,这里的可以表示多项式或者单项式;
如果 与 成反比例,则 (k 为常数,k≠0)
或者k 为常数,k≠0)
新知讲解
典例小结
(2)反比例关系与反比例函数的区别与联系:
两个变量成反比例关系,但不一定是反比例函数,但反比例函数 ()中的两个变量之间一定成反比例关系;
比如 与 成反比例,则 (k 为常数,k≠0)
此时并不是的反比例函数
反比例关系
反比例函数
典例实践
例2. 已知 与 成反比例,并且当时,
(1)写出关于的函数解析式;
(2)当时,求的值;
解
将中得
典例实践
例2. 已知 与 成反比例,并且当时,
(1)写出关于的函数解析式;
(2)当时,求的值;
(2)解
将 中得
中
得
例3. 已知 的反比例函数,并且当时,
(1)写出关于的函数解析式;
(2)当时,求的值;
解
将中得
(2)将 中
得
新知讲解
二、利用待定系数法求反比例函数的解析式
步骤:
①设(设出反比例函数解析式 () );
②代(将一组自变量与函数的对应值)代入解析式,
得到关于待定系数k的方程);
③解(解方程,求出待定系数k);
④写 (代入k,写出反比例函数解析式).
课堂练习
用函数解析式表示下列问题中变量间的对应关系,并判断是否是反比例函数;
(1)一个游泳池的容积为 1 800 m3,游泳池注满水所用时间 t(单位:h)
随注水速度 v(单位:m3/h)的变化而变化;
是反比例函数,其中
(2)某长方体的体积为 1 000 cm3,长方体的高 h(单位:cm)随底面积 S(单位:cm2)的变化而变化;
是反比例函数,其中
课堂练习
(3)一个物体重 100 N,物体对地面的压强 p(单位:Pa)随物体与地面的接触面积 S(单位:m2)的变化而变化.
P
(4)果果用完30元买练习本,买的练习本的本书y(单位:本)随练习本的价格x(单位:元)的变化而变化.
是反比例函数,其中
是反比例函数,其中
课堂练习
2. 已知反比例函数的解析式为 y = ,则 的取值范围是( )
课堂练习
3. 当为何值时,关于的反比例函数?
解关于的反比例函数
则
得
得
∴当 时,关于的反比例函数
课堂练习
拓展1. 当为何值时,关于的正比例函数?
解关于的正比例函数
则
得
得
∴当 时,关于的反比例函数
课堂练习
拓展2. 当为何值时,关于的二次函数?
解关于的二次函数
则
得
得
∴当 时,关于的二次函数
课堂小结
反比例函数
形如 (为常数,) 的函数,叫做反比例函数
概念
解析式的形式
(
待定系数法
①设:设反比例函数解析式为
(;
②代:将一对对应值代入解析式,
得到关于k的方程;
③解:解方程,求出k;
④写:代入k写出解析式
