专题03勾股定理(考点串讲)-七年级数学上学期期中考点大串讲(鲁教版五四制)
文档属性
| 名称 | 专题03勾股定理(考点串讲)-七年级数学上学期期中考点大串讲(鲁教版五四制) |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 00:00:00 | ||
图片预览









文档简介
(共42张PPT)
七年级新鲁教版(2024)数学上册期中考点大串讲
串讲03 勾股定理
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
四大常考点:知识梳理
六大题型典例剖析+技巧点拨+举一反三
三大易错易混经典例题+针对训练
期中真题对应考点练
考点透视
知识点1.勾股定理
(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
(2)勾股定理应用的前提条件是在直角三角形中.
知识点2.勾股定理的证明
(1)勾股定理的证明方法有很多种,教材是采用了拼图的方法证明的.先利用拼图的方法,然后再利用面积相等证明勾股定理.
(2)证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理.
知识点3.勾股定理的逆定理
(1)勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
说明:
①勾股定理的逆定理验证利用了三角形的全等.
②勾股定理的逆定理将数转化为形,作用是判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.
知识点4.勾股数
勾股数:满足a2+b2=c2 的三个正整数,称为勾股数.
说明:
①三个数必须是正整数,例如:2.5、6、6.5满足a2+b2=c2,但是它们不是正整数,所以它们不是够勾股数.
②一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.
③记住常用的勾股数再做题可以提高速度.如:3,4,5;6,8,10;5,12,13;…
知识点5.勾股定理的应用
(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.
(2)在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
(3)常见的类型:①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.
②由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.
③勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.
④勾股定理在数轴上表示无理数的应用:利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
题型剖析
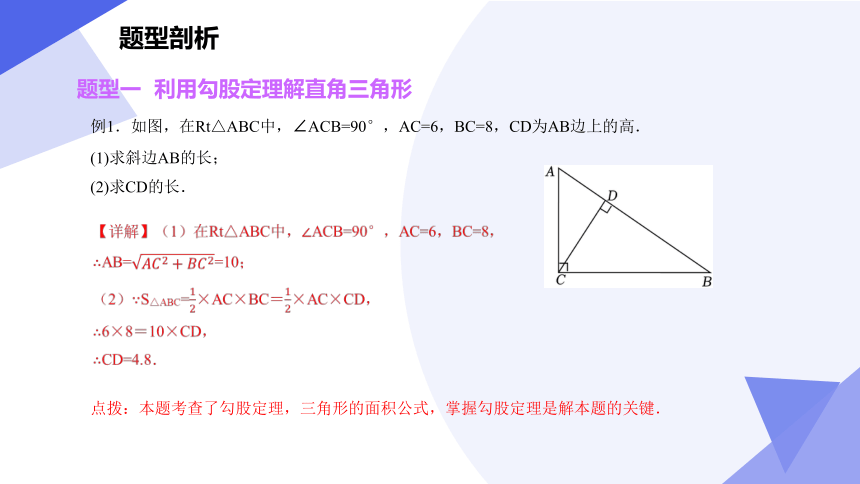
题型一 利用勾股定理解直角三角形
例1.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD为AB边上的高.
(1)求斜边AB的长;
(2)求CD的长.
【详解】(1)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB==10;
(2)∵S△ABC=×AC×BC=×AC×CD,
∴6×8=10×CD,
∴CD=4.8.
点拨:本题考查了勾股定理,三角形的面积公式,掌握勾股定理是解本题的关键.
举一反三
1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得AC=6cm,BC=10cm.求A,B两点间的距离.
【详解】解:由题意得:AB⊥AC,
∵AC=6cm,BC=10cm,
∴AB==8cm;
答:A、B两点间的距离为8cm.
【分析】本题主要考查勾股定理,熟练掌握勾股定理是解题的关键;由题意易得AB⊥AC,然后根据勾股定理可进行求解.
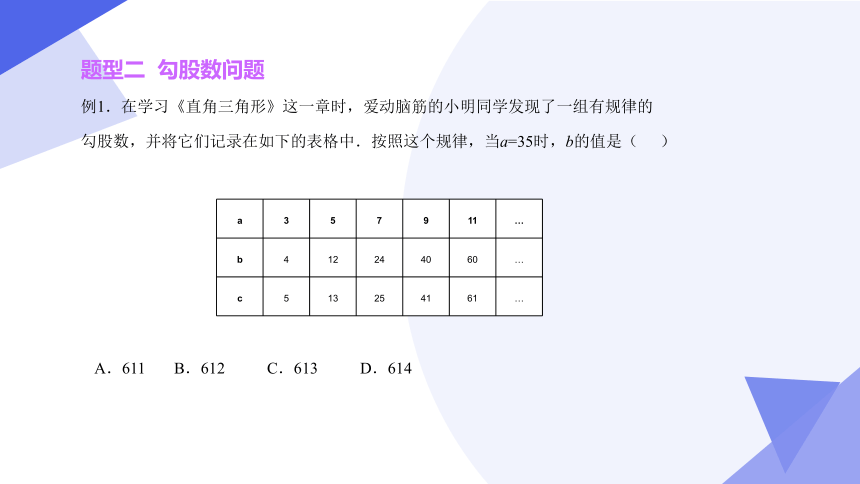
题型二 勾股数问题
例1.在学习《直角三角形》这一章时,爱动脑筋的小明同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.按照这个规律,当a=35时,b的值是( )
a 3 5 7 9 11 …
b 4 12 24 40 60 …
c 5 13 25 41 61 …
A.611 B.612 C.613 D.614
【详解】解:由表格中的数据得:,c=b+1,
∴,
∴当a=35时,则,
解得:b=612,
点拨:本题考查了勾股数,掌握表中数据的变化规律,找到数据的关系是解答本题的关键.由表格中的数据得:,c=b+1,即可得出,代入a=35即可求出b的值.
举一反三
1.下列各组数中不是勾股数的是( )
A.3、4、5 B.4、5、6 C.6、8、10 D.9、40、41
【答案】B
【详解】解:A、因为,所以3、4、5是勾股数,不符合题意;
B、 因为,所以4、5、6不是勾股数,符合题意;
C、 因为,所以6、8、10是勾股数,不符合题意;
D、 因为,所以9、40、41是勾股数,不符合题意.
故选:B.
点拨:本题主要考查了勾股数的知识,理解并掌握勾股数的定义是解题关键.满足的三个正整数,称为勾股数.根据勾股数的定义逐项分析判断即可.
题型三 勾股定理在网格中的应用
例1.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点都在小正方形网格线的交点上.求△ABC的周长及AB边上的高.
【详解】解:由题意可得BC=3,
由勾股定理可得AC=,AB=,
∴△ABC的周长为3+5+.
设AB边上的高为h,
∴S△ABC=
则5h=3×3,
∴h=
∴AB边上的高是.
点拨:此题考查了勾股定理,等面积法求线段长度,
首先根据网格的特点和勾股定理求出BC=3, AC=,AB=,然后根据三角形周长公式求解,然后利用等面积法求解即可.
举一反三
1.如图,网格小正方形的边长都为1,在△ABC中,试利用格点分别画出:边AC边上的中线BM、边AB边上的高CH,并判断△ABC的形状.
【详解】解:如图,△ABC的中线BM,高CH即为所求作.
∵AC==
∴AC=AB,
∴△ABC是等腰三角形.
点拨:本题考查作图-复杂作图,三角形的中线,高,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
根据三角形的中线,高的定义作出图形即可,利用勾股定理求出AC,AB,可得AC=AB.
题型四 勾股定理的证明方法
例1.请阅读下列材料,并完成相应的任务.
勾股定理的证明.勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”,而且在高等数学和其他学科中也有着极为广泛的应用.正因为这样,世界上几个文明古国都已发现并且进行了广泛深入的研究,我国三国时期的数学家赵爽在为《周髀算经》作注时,利用“弦图”巧妙地给出了勾股定理的证明,这个证明是有史以来四百多种证明中最巧妙的证法之一.
在西方勾股定理也称毕达哥拉斯定理.其中,美国第二十任总统詹姆斯·伽菲尔德的证法在数学史上被传为佳话.他将两个直角三角形拼成一个梯形(如图),根据基本活动经验:“表示同一个量(这里指梯形的面积)的两个代数式相等”进行证明.任务:
(1)勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么_______.
(2)根据阅读内容,图中梯形的面积分别可以表示为______和_______.
(3)根据(2)中的结果,写出证明过程.
【详解】(1)解:由勾股定理得,
故答案为:;
(2)解:根据梯形面积公式可得梯形面积为;
根据梯形面积等于三个直角三角形的面积可得梯形面积为=ab+,
故答案为:,;
(3)证明:∵(2)中两种表示方法表示的梯形面积相等,
∴,
∴,
∴.
点拨:本题主要考查了勾股定理及其证明方法:
(1)直角三角形中,两直角边的平方和等于斜边的平方,据此求解即可;
(2)根据梯形的面积公式以及梯形的面积等于三个直角三角形的面积进行求解即可 ;
(3)根据(2)中两种表示方法表示的面积相等列式证明即可.
举一反三
1.现有4个全等的直角三角形(阴影部分),直角边长分别为a、b,斜边长为c,将它们拼合为如图的形状.
(1)添加如图辅助线,根据该图,可以用两种不同的方法计算整个组合图形的面积,通过面积相等,从而证明勾股定理,请你将下面的证明过程补充完整:整个组合图形面积表示,方法一:以c为边的正方形的面积+两个直角三角形的面积,即最后化简为 ;方法二:以a和b为边的两个小正方形的面积+两个直角三角形的面积,即最后化简为 ;根据面积相等,直接得等式 ,化简最后结果是 ,从而证明勾股定理.
(2)当a=3,b=4时,求空白部分的面积.
【详解】(1)解:方法一:以c为边的正方形的面积+两个直角三角形的面积为:,
即最后化简为;
方法二:以a和b为边的两个小正方形的面积+两个直角三角形的面积,即最后化简为;
根据面积相等,得: =,
化简最后结果是 =.
故答案为:,, =,=
(2)解:根据题意得:空白部分的面积为:
当a=3,b=4时,原式=32+42-3×4=13.
点拨:本题考查了勾股定理的几何背景,代数式求值,正确识图是解题的关键.
(1)根据题意和图形即可求解;
(2)根据空白部分的面积等于以c为边的正方形的面积减去2个直角三角形的面积可得空白部分的面积为,再把a=3,b=4代入计算即可求解.
题型五 勾股定理逆定理的应用
例1.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
【详解】(1)解:是,
理由是:在△CHB中,
∵CH2+BH2=2.42+1.82=9=BC2,,
∴CH2+BH2=BC2
∴CH⊥AB,
∴CH是从村庄C到河边的最近路;
(2)解:设AC=x,则AH=x-1.8,CH=2.4
由勾股定理得:AC2=AH2+CH2
∴x2= (x-1.8)2+2.42
解得x =2.5
答:原来的路线AC的长为2.5千米.
点拨:此题考查勾股定理的应用,关键是根据勾股定理的逆定理和定理解答.
(1)根据勾股定理的逆定理解答即可;
(2)根据勾股定理解答即可.
举一反三
1.某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行20海里,“海天”号每小时航行15海里,它们离开港口两个小时后相距50海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【详解】解:由题意可得RP=2×15=30海里, PQ=2×20=40海里,QR=50海里,
则302+402=502,
∴RP2+PQ2=QR2,
∴△RPQ是直角三角形,
∴∠RPQ=90°,
∵“远航”号沿东北方向航行,
∴∠QPS=45°,
∴∠RPS=45°,
∴“海天”号沿北偏西45°方向航行.
点拨:本题主要考查了勾股定理的逆定理的应用,由题意可得RP=30海里,PQ=2×20=40海里,QR=50海里,根据勾股定理逆定理得△RPQ是直角三角形,从而有∠RPQ=90°,又“远航”号沿东北方向航行,则∠QPS=45°,最后由角度和差即可求解,掌握勾股定理的逆定理是解题关键.
题型六 勾股定理定理的应用举例
例1.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A、B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C会受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
【详解】(1)解:如图所示,过点C作CD⊥AB于D点,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,
∴AC×BC=AB×CD,
∴300×400=500CD,
∴CD=240km,
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C会受到台风影响;
(2)解:由(1)得CD=240km,
如图所示,当EC=FC=250km时,即台风经过EF段时,正好影响到海港C,此时△ECF为等腰三角形,
∵ED==70km,
∴EF=140km,
∵台风的速度为20km/h,
∴140÷20=7h,
∴台风影响该海港持续的时间有7h.
点拨:本题主要考查了勾股定理的逆定理,勾股定理,等腰三角形的性质,熟练掌握勾股定理的逆定理,勾股定理,等腰三角形的性质是解题的关键.
(1)过点C作CD⊥AB于D点,根据勾股定理逆定理可得△ABC为直角三角形,再由三角形的面积公式可得CD=240km,即可求解;
(2)当EC=FC=250km时,即台风经过EF段时,正好影响到海港C,此时△ECF为等腰三角形,根据勾股定理求出ED=70km,从而得到EF=140km,即可求解.
易错易混
易错题型一——求大树折断前的高度
1.如图,一棵树在离地面1.2米处断裂,树的顶部落在离底部1.6米处,树折断之前有( )米
A.2.2 B.2.8 C.3.2 D.4
【答案】C
【详解】如图,
由题意可知,BC=1.2米,AB=1.6米,∠ABC=90°,
由勾股定理得:
AC===2(米)
∴BC+AC=1.2+2=3.2(米)
即树折断之前有3.2米.
故选:C.
点拨:此题考查了勾股定理的应用,根据勾股定理求出AC的长是解题的关键.
由勾股定理求出AC的长,即可解决问题.
易错题型二——解决水杯中的筷子问题
例1.如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
A.12cm≤h≤19cm B.12cm≤h≤17cm
C.11cm≤h≤12cm D.5cm≤h≤12cm
【答案】C
【详解】解:由题意可知,h最长是筷子的长度减去杯子的高度,即hmax=24-12=12cm,
h最短是筷子的长度减去杯子斜边长度,
由勾股定理得,杯子的斜边长度 =13cm,即hmin=24-13=11cm,
∴h的取值范围是11cm≤h≤12cm,
故选:C.
点拨:本题考查了勾股定理的应用,正确理解题意解题关键.根据题意可知,h最长是筷子的长度减去杯子的高度,h最短是筷子的长度减去杯子斜边长度,利用勾股定理求出杯子的斜边长度,即可求出h的取值范围.
易错题型三——求台阶上地毯长度
例1.如图,楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?(精确到0.1m)
【详解】解:如图,由勾股定理得,AB2=BC2+AC2,
∴BC==米,
∴AC+BC=2+≈5.5米,
答:地毯的长度至少需要5.5米.
点拨:考查了勾股定理的应用,根据图形可得,地毯的长度等于AC+BC,利用勾股定理求出BC的长,即可求解,理解地毯的长度等于AC+BC是解题的关键.
易错题针对训练
1.如图,在一个高为3米的楼梯表面铺地毯,地毯总长度为7米,则楼梯斜面AB长为( )
A.4米 B.5米 C.6米 D.7米
由题意得AC+BC=7米,
∵AC=3米,
∴BC=4米,
∴AB2=BC2+AC2=25则AB=5米,
故选:B.
点拨:本题主要考查勾股定理,由勾股定理及平移的思想可进行求解.
【详解】解:如图所示,
【答案】B
2.一支铅笔斜放在圆柱体的笔筒中,如图所示,笔筒的内部底面直径是6cm,内壁高8cm.若这支铅笔在笔筒外面部分长度是5cm,则这支铅笔的长度是( )cm.
A.10 B.15 C.20 D.25
【答案】B
【详解】解:如图:
根据题意可得图形:AB=8cm,BC=6cm,
在Rt△ABC中:AC==10cm,
∵这支铅笔在笔筒外面部分长度是5cm,
∴这支铅笔的长度是10+5=15(cm).
故选:B.
点拨:首先根据题意画出图形,利用勾股定理计算出AC的长度.然后结合题意即可求解.
此题主要考查了勾股定理的应用,正确得出笔筒内铅笔的长度是解决问题的关键.
押题预测
练习&巩固
1.[2023年烟台市7年级上册期末] 如图,庭院中有两棵树,小鸟要从一棵高10m的树顶飞到一棵高4m的树顶上,两棵树相距8m,则小鸟至少要飞 米.
【答案】10
【详解】解:如图,连接AB,过点B作BC⊥AD
∵∠ADH=∠BCD=∠BHD=90°
∴四边形BCDH矩形
∴BH=DC=4cm,BC=DH=8m
∴AC=AD-CD=10-4=6(m),
在Rt△ABC中,由勾股定理得,
AB==10(m),
则小鸟至少要飞10m,
故答案为:10.
点拨:根据勾股定理求出AB的长即可.
本题考查了勾股定理的应用,熟记勾股定理是解题的关键.
2. [2023年济宁市7年级上册期末] 为了培养学生的数学核心素养,提高学生发现问题,分析问题,解决问题的能力.2024年昭通市某学校的156班组织了一次课外研学活动.在研学活动中,王宇同学欲控制遥控轮船匀速垂直横渡一条河,但由于水流的影响,实际上岸地点F与欲到达地点E相距10米,结果轮船在水中实际航行的路程HF比河的宽度EH多2米,则河的宽度EH是( ).
A.8米 B.12米 C.16米 D.24米
【答案】D
【详解】解:根据题意可知EF=10米,
设EH=x,则HF= x +2,
Rt△EFH中,由勾股定理得FH2=EF2+EH2,
即(x+2)2=102+x2,
解得x=24.
∴该河的宽度EH为24米.
故选:D.
点拨:本题考查了勾股定理的应用,根据题意可知△EFH为直角三角形,根据勾股定理列方程就可求出直角边EH的长度.
3. [2023年泰安市7年级期中] 2021年9月23日是第四个中国农民丰收节,小彬用3D打印机制作了一个底面周长为18cm,高为12cm的圆柱状粮仓模型,如图所示,BC是底面直径,AB是圆柱的高.现要在此模型的侧面贴一圈彩色装饰带,且装饰带经过A,C两点(接头不计),则装饰带的长度最短为 cm.
【答案】30
【详解】解:如图,圆柱的侧面展开图为长方形,AC=A’C,且点C为BB’的中点,
∵AB=12,BC=×18=9,
∴装饰带的长度=2AC=2×=30(cm),
故答案为:30.
点拨:由平面图形的折叠及立体图形的表面展开图的特点解题.此题主要考查了勾股定理,平面展开-最短路线问题,以及学生的立体思维能力.解题时注意:圆柱的侧面展开图是长方形.
4. [2023年济宁市7年级上册月考]如图,有一个绳索拉直的木马秋干,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,求此时木马上升的高度.
【答案】木马上升的高度为1米
【详解】解:如图,过点C作CF⊥AB于点F,则CF=DE=3米,
由题意得:AC=AB=5米,
在Rt△ACF中,由勾股定理得:AF===4米,
则BF=AB-AF=5-4=1米,
即木马上升的高度为1米.
点拨:本题主要考查了勾股定理的应用.过点C作CF⊥AB于点F,则CF=DE=3米,在Rt△ACF中,由勾股定理可得BF的长,即可求解.
七年级新鲁教版(2024)数学上册期中考点大串讲
串讲03 勾股定理
01
02
04
03
目
录
易错易混
题型剖析
考点透视
押题预测
四大常考点:知识梳理
六大题型典例剖析+技巧点拨+举一反三
三大易错易混经典例题+针对训练
期中真题对应考点练
考点透视
知识点1.勾股定理
(1)勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.
如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.
(2)勾股定理应用的前提条件是在直角三角形中.
知识点2.勾股定理的证明
(1)勾股定理的证明方法有很多种,教材是采用了拼图的方法证明的.先利用拼图的方法,然后再利用面积相等证明勾股定理.
(2)证明勾股定理时,用几个全等的直角三角形拼成一个规则的图形,然后利用大图形的面积等于几个小图形的面积和化简整理得到勾股定理.
知识点3.勾股定理的逆定理
(1)勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
说明:
①勾股定理的逆定理验证利用了三角形的全等.
②勾股定理的逆定理将数转化为形,作用是判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.
知识点4.勾股数
勾股数:满足a2+b2=c2 的三个正整数,称为勾股数.
说明:
①三个数必须是正整数,例如:2.5、6、6.5满足a2+b2=c2,但是它们不是正整数,所以它们不是够勾股数.
②一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数.
③记住常用的勾股数再做题可以提高速度.如:3,4,5;6,8,10;5,12,13;…
知识点5.勾股定理的应用
(1)在不规则的几何图形中,通常添加辅助线得到直角三角形.
(2)在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
(3)常见的类型:①勾股定理在几何中的应用:利用勾股定理求几何图形的面积和有关线段的长度.
②由勾股定理演变的结论:分别以一个直角三角形的三边为边长向外作正多边形,以斜边为边长的多边形的面积等于以直角边为边长的多边形的面积和.
③勾股定理在实际问题中的应用:运用勾股定理的数学模型解决现实世界的实际问题.
④勾股定理在数轴上表示无理数的应用:利用勾股定理把一个无理数表示成直角边是两个正整数的直角三角形的斜边.
题型剖析
题型一 利用勾股定理解直角三角形
例1.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,CD为AB边上的高.
(1)求斜边AB的长;
(2)求CD的长.
【详解】(1)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB==10;
(2)∵S△ABC=×AC×BC=×AC×CD,
∴6×8=10×CD,
∴CD=4.8.
点拨:本题考查了勾股定理,三角形的面积公式,掌握勾股定理是解本题的关键.
举一反三
1.如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得AC=6cm,BC=10cm.求A,B两点间的距离.
【详解】解:由题意得:AB⊥AC,
∵AC=6cm,BC=10cm,
∴AB==8cm;
答:A、B两点间的距离为8cm.
【分析】本题主要考查勾股定理,熟练掌握勾股定理是解题的关键;由题意易得AB⊥AC,然后根据勾股定理可进行求解.
题型二 勾股数问题
例1.在学习《直角三角形》这一章时,爱动脑筋的小明同学发现了一组有规律的勾股数,并将它们记录在如下的表格中.按照这个规律,当a=35时,b的值是( )
a 3 5 7 9 11 …
b 4 12 24 40 60 …
c 5 13 25 41 61 …
A.611 B.612 C.613 D.614
【详解】解:由表格中的数据得:,c=b+1,
∴,
∴当a=35时,则,
解得:b=612,
点拨:本题考查了勾股数,掌握表中数据的变化规律,找到数据的关系是解答本题的关键.由表格中的数据得:,c=b+1,即可得出,代入a=35即可求出b的值.
举一反三
1.下列各组数中不是勾股数的是( )
A.3、4、5 B.4、5、6 C.6、8、10 D.9、40、41
【答案】B
【详解】解:A、因为,所以3、4、5是勾股数,不符合题意;
B、 因为,所以4、5、6不是勾股数,符合题意;
C、 因为,所以6、8、10是勾股数,不符合题意;
D、 因为,所以9、40、41是勾股数,不符合题意.
故选:B.
点拨:本题主要考查了勾股数的知识,理解并掌握勾股数的定义是解题关键.满足的三个正整数,称为勾股数.根据勾股数的定义逐项分析判断即可.
题型三 勾股定理在网格中的应用
例1.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点都在小正方形网格线的交点上.求△ABC的周长及AB边上的高.
【详解】解:由题意可得BC=3,
由勾股定理可得AC=,AB=,
∴△ABC的周长为3+5+.
设AB边上的高为h,
∴S△ABC=
则5h=3×3,
∴h=
∴AB边上的高是.
点拨:此题考查了勾股定理,等面积法求线段长度,
首先根据网格的特点和勾股定理求出BC=3, AC=,AB=,然后根据三角形周长公式求解,然后利用等面积法求解即可.
举一反三
1.如图,网格小正方形的边长都为1,在△ABC中,试利用格点分别画出:边AC边上的中线BM、边AB边上的高CH,并判断△ABC的形状.
【详解】解:如图,△ABC的中线BM,高CH即为所求作.
∵AC==
∴AC=AB,
∴△ABC是等腰三角形.
点拨:本题考查作图-复杂作图,三角形的中线,高,勾股定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
根据三角形的中线,高的定义作出图形即可,利用勾股定理求出AC,AB,可得AC=AB.
题型四 勾股定理的证明方法
例1.请阅读下列材料,并完成相应的任务.
勾股定理的证明.勾股定理,是几何学中一颗光彩夺目的明珠,被称为“几何学的基石”,而且在高等数学和其他学科中也有着极为广泛的应用.正因为这样,世界上几个文明古国都已发现并且进行了广泛深入的研究,我国三国时期的数学家赵爽在为《周髀算经》作注时,利用“弦图”巧妙地给出了勾股定理的证明,这个证明是有史以来四百多种证明中最巧妙的证法之一.
在西方勾股定理也称毕达哥拉斯定理.其中,美国第二十任总统詹姆斯·伽菲尔德的证法在数学史上被传为佳话.他将两个直角三角形拼成一个梯形(如图),根据基本活动经验:“表示同一个量(这里指梯形的面积)的两个代数式相等”进行证明.任务:
(1)勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么_______.
(2)根据阅读内容,图中梯形的面积分别可以表示为______和_______.
(3)根据(2)中的结果,写出证明过程.
【详解】(1)解:由勾股定理得,
故答案为:;
(2)解:根据梯形面积公式可得梯形面积为;
根据梯形面积等于三个直角三角形的面积可得梯形面积为=ab+,
故答案为:,;
(3)证明:∵(2)中两种表示方法表示的梯形面积相等,
∴,
∴,
∴.
点拨:本题主要考查了勾股定理及其证明方法:
(1)直角三角形中,两直角边的平方和等于斜边的平方,据此求解即可;
(2)根据梯形的面积公式以及梯形的面积等于三个直角三角形的面积进行求解即可 ;
(3)根据(2)中两种表示方法表示的面积相等列式证明即可.
举一反三
1.现有4个全等的直角三角形(阴影部分),直角边长分别为a、b,斜边长为c,将它们拼合为如图的形状.
(1)添加如图辅助线,根据该图,可以用两种不同的方法计算整个组合图形的面积,通过面积相等,从而证明勾股定理,请你将下面的证明过程补充完整:整个组合图形面积表示,方法一:以c为边的正方形的面积+两个直角三角形的面积,即最后化简为 ;方法二:以a和b为边的两个小正方形的面积+两个直角三角形的面积,即最后化简为 ;根据面积相等,直接得等式 ,化简最后结果是 ,从而证明勾股定理.
(2)当a=3,b=4时,求空白部分的面积.
【详解】(1)解:方法一:以c为边的正方形的面积+两个直角三角形的面积为:,
即最后化简为;
方法二:以a和b为边的两个小正方形的面积+两个直角三角形的面积,即最后化简为;
根据面积相等,得: =,
化简最后结果是 =.
故答案为:,, =,=
(2)解:根据题意得:空白部分的面积为:
当a=3,b=4时,原式=32+42-3×4=13.
点拨:本题考查了勾股定理的几何背景,代数式求值,正确识图是解题的关键.
(1)根据题意和图形即可求解;
(2)根据空白部分的面积等于以c为边的正方形的面积减去2个直角三角形的面积可得空白部分的面积为,再把a=3,b=4代入计算即可求解.
题型五 勾股定理逆定理的应用
例1.在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
【详解】(1)解:是,
理由是:在△CHB中,
∵CH2+BH2=2.42+1.82=9=BC2,,
∴CH2+BH2=BC2
∴CH⊥AB,
∴CH是从村庄C到河边的最近路;
(2)解:设AC=x,则AH=x-1.8,CH=2.4
由勾股定理得:AC2=AH2+CH2
∴x2= (x-1.8)2+2.42
解得x =2.5
答:原来的路线AC的长为2.5千米.
点拨:此题考查勾股定理的应用,关键是根据勾股定理的逆定理和定理解答.
(1)根据勾股定理的逆定理解答即可;
(2)根据勾股定理解答即可.
举一反三
1.某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行20海里,“海天”号每小时航行15海里,它们离开港口两个小时后相距50海里,如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【详解】解:由题意可得RP=2×15=30海里, PQ=2×20=40海里,QR=50海里,
则302+402=502,
∴RP2+PQ2=QR2,
∴△RPQ是直角三角形,
∴∠RPQ=90°,
∵“远航”号沿东北方向航行,
∴∠QPS=45°,
∴∠RPS=45°,
∴“海天”号沿北偏西45°方向航行.
点拨:本题主要考查了勾股定理的逆定理的应用,由题意可得RP=30海里,PQ=2×20=40海里,QR=50海里,根据勾股定理逆定理得△RPQ是直角三角形,从而有∠RPQ=90°,又“远航”号沿东北方向航行,则∠QPS=45°,最后由角度和差即可求解,掌握勾股定理的逆定理是解题关键.
题型六 勾股定理定理的应用举例
例1.台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力,如图,有一台风中心沿东西方向AB由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A、B的距离分别为300km和400km,又AB=500km,以台风中心为圆心周围250km以内为受影响区域.
(1)海港C会受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
【详解】(1)解:如图所示,过点C作CD⊥AB于D点,
∵AC=300km,BC=400km,AB=500km,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,
∴AC×BC=AB×CD,
∴300×400=500CD,
∴CD=240km,
∵以台风中心为圆心周围250km以内为受影响区域,
∴海港C会受到台风影响;
(2)解:由(1)得CD=240km,
如图所示,当EC=FC=250km时,即台风经过EF段时,正好影响到海港C,此时△ECF为等腰三角形,
∵ED==70km,
∴EF=140km,
∵台风的速度为20km/h,
∴140÷20=7h,
∴台风影响该海港持续的时间有7h.
点拨:本题主要考查了勾股定理的逆定理,勾股定理,等腰三角形的性质,熟练掌握勾股定理的逆定理,勾股定理,等腰三角形的性质是解题的关键.
(1)过点C作CD⊥AB于D点,根据勾股定理逆定理可得△ABC为直角三角形,再由三角形的面积公式可得CD=240km,即可求解;
(2)当EC=FC=250km时,即台风经过EF段时,正好影响到海港C,此时△ECF为等腰三角形,根据勾股定理求出ED=70km,从而得到EF=140km,即可求解.
易错易混
易错题型一——求大树折断前的高度
1.如图,一棵树在离地面1.2米处断裂,树的顶部落在离底部1.6米处,树折断之前有( )米
A.2.2 B.2.8 C.3.2 D.4
【答案】C
【详解】如图,
由题意可知,BC=1.2米,AB=1.6米,∠ABC=90°,
由勾股定理得:
AC===2(米)
∴BC+AC=1.2+2=3.2(米)
即树折断之前有3.2米.
故选:C.
点拨:此题考查了勾股定理的应用,根据勾股定理求出AC的长是解题的关键.
由勾股定理求出AC的长,即可解决问题.
易错题型二——解决水杯中的筷子问题
例1.如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
A.12cm≤h≤19cm B.12cm≤h≤17cm
C.11cm≤h≤12cm D.5cm≤h≤12cm
【答案】C
【详解】解:由题意可知,h最长是筷子的长度减去杯子的高度,即hmax=24-12=12cm,
h最短是筷子的长度减去杯子斜边长度,
由勾股定理得,杯子的斜边长度 =13cm,即hmin=24-13=11cm,
∴h的取值范围是11cm≤h≤12cm,
故选:C.
点拨:本题考查了勾股定理的应用,正确理解题意解题关键.根据题意可知,h最长是筷子的长度减去杯子的高度,h最短是筷子的长度减去杯子斜边长度,利用勾股定理求出杯子的斜边长度,即可求出h的取值范围.
易错题型三——求台阶上地毯长度
例1.如图,楼梯的高度为2m,楼梯坡面的长度为4m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?(精确到0.1m)
【详解】解:如图,由勾股定理得,AB2=BC2+AC2,
∴BC==米,
∴AC+BC=2+≈5.5米,
答:地毯的长度至少需要5.5米.
点拨:考查了勾股定理的应用,根据图形可得,地毯的长度等于AC+BC,利用勾股定理求出BC的长,即可求解,理解地毯的长度等于AC+BC是解题的关键.
易错题针对训练
1.如图,在一个高为3米的楼梯表面铺地毯,地毯总长度为7米,则楼梯斜面AB长为( )
A.4米 B.5米 C.6米 D.7米
由题意得AC+BC=7米,
∵AC=3米,
∴BC=4米,
∴AB2=BC2+AC2=25则AB=5米,
故选:B.
点拨:本题主要考查勾股定理,由勾股定理及平移的思想可进行求解.
【详解】解:如图所示,
【答案】B
2.一支铅笔斜放在圆柱体的笔筒中,如图所示,笔筒的内部底面直径是6cm,内壁高8cm.若这支铅笔在笔筒外面部分长度是5cm,则这支铅笔的长度是( )cm.
A.10 B.15 C.20 D.25
【答案】B
【详解】解:如图:
根据题意可得图形:AB=8cm,BC=6cm,
在Rt△ABC中:AC==10cm,
∵这支铅笔在笔筒外面部分长度是5cm,
∴这支铅笔的长度是10+5=15(cm).
故选:B.
点拨:首先根据题意画出图形,利用勾股定理计算出AC的长度.然后结合题意即可求解.
此题主要考查了勾股定理的应用,正确得出笔筒内铅笔的长度是解决问题的关键.
押题预测
练习&巩固
1.[2023年烟台市7年级上册期末] 如图,庭院中有两棵树,小鸟要从一棵高10m的树顶飞到一棵高4m的树顶上,两棵树相距8m,则小鸟至少要飞 米.
【答案】10
【详解】解:如图,连接AB,过点B作BC⊥AD
∵∠ADH=∠BCD=∠BHD=90°
∴四边形BCDH矩形
∴BH=DC=4cm,BC=DH=8m
∴AC=AD-CD=10-4=6(m),
在Rt△ABC中,由勾股定理得,
AB==10(m),
则小鸟至少要飞10m,
故答案为:10.
点拨:根据勾股定理求出AB的长即可.
本题考查了勾股定理的应用,熟记勾股定理是解题的关键.
2. [2023年济宁市7年级上册期末] 为了培养学生的数学核心素养,提高学生发现问题,分析问题,解决问题的能力.2024年昭通市某学校的156班组织了一次课外研学活动.在研学活动中,王宇同学欲控制遥控轮船匀速垂直横渡一条河,但由于水流的影响,实际上岸地点F与欲到达地点E相距10米,结果轮船在水中实际航行的路程HF比河的宽度EH多2米,则河的宽度EH是( ).
A.8米 B.12米 C.16米 D.24米
【答案】D
【详解】解:根据题意可知EF=10米,
设EH=x,则HF= x +2,
Rt△EFH中,由勾股定理得FH2=EF2+EH2,
即(x+2)2=102+x2,
解得x=24.
∴该河的宽度EH为24米.
故选:D.
点拨:本题考查了勾股定理的应用,根据题意可知△EFH为直角三角形,根据勾股定理列方程就可求出直角边EH的长度.
3. [2023年泰安市7年级期中] 2021年9月23日是第四个中国农民丰收节,小彬用3D打印机制作了一个底面周长为18cm,高为12cm的圆柱状粮仓模型,如图所示,BC是底面直径,AB是圆柱的高.现要在此模型的侧面贴一圈彩色装饰带,且装饰带经过A,C两点(接头不计),则装饰带的长度最短为 cm.
【答案】30
【详解】解:如图,圆柱的侧面展开图为长方形,AC=A’C,且点C为BB’的中点,
∵AB=12,BC=×18=9,
∴装饰带的长度=2AC=2×=30(cm),
故答案为:30.
点拨:由平面图形的折叠及立体图形的表面展开图的特点解题.此题主要考查了勾股定理,平面展开-最短路线问题,以及学生的立体思维能力.解题时注意:圆柱的侧面展开图是长方形.
4. [2023年济宁市7年级上册月考]如图,有一个绳索拉直的木马秋干,绳索AB的长度为5米,若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,求此时木马上升的高度.
【答案】木马上升的高度为1米
【详解】解:如图,过点C作CF⊥AB于点F,则CF=DE=3米,
由题意得:AC=AB=5米,
在Rt△ACF中,由勾股定理得:AF===4米,
则BF=AB-AF=5-4=1米,
即木马上升的高度为1米.
点拨:本题主要考查了勾股定理的应用.过点C作CF⊥AB于点F,则CF=DE=3米,在Rt△ACF中,由勾股定理可得BF的长,即可求解.
