《旋转》全章复习与巩固--知识讲解(提高)
文档属性
| 名称 | 《旋转》全章复习与巩固--知识讲解(提高) |  | |
| 格式 | doc | ||
| 文件大小 | 292.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 11:07:19 | ||
图片预览


文档简介
人教版九上数学资料
《旋转》全章复习与巩固(提高)知识讲解
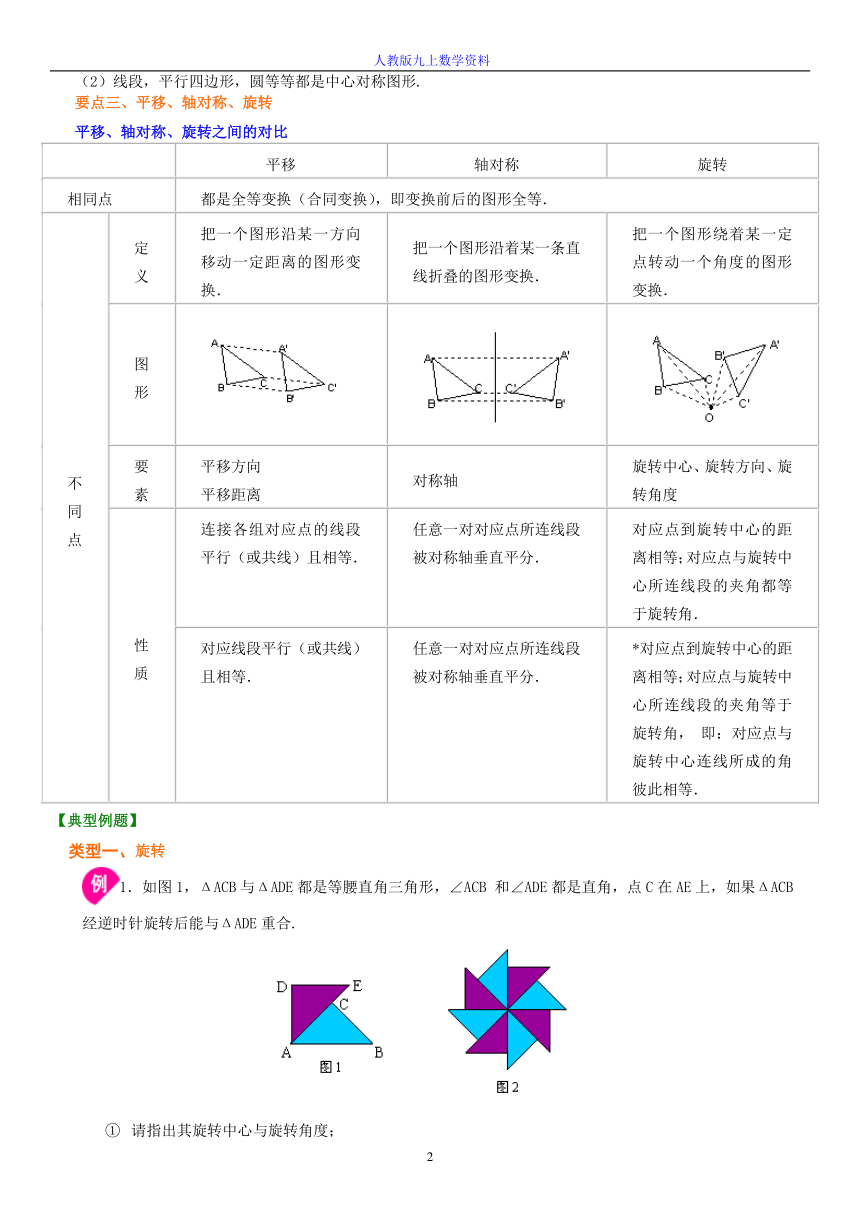
【知识网络】
【要点梳理】要点一、旋转
1. 旋转的概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转..点O叫做旋转中心,转动的角叫做旋转角(如∠AO A′),如果图形上的点A经过旋转变为点A′,那么,这两个点叫做这个旋转的对应点.
要点诠释:旋转的三个要素:旋转中心、旋转方向和旋转角度.
2.旋转的性质: (1)对应点到旋转中心的距离相等(OA= OA′);
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等(△ABC≌△).
要点诠释:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.
3. 旋转的作图: 在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键
沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.
要点诠释:
作图的步骤:(1)连接图形中的每一个关键点与旋转中心;
(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);
(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;
(4)连接所得到的各对应点.
要点二、特殊的旋转—中心对称
1.中心对称: 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.
要点诠释:(1)有两个图形,能够完全重合,即形状大小都相同;
(2)位置必须满足一个条件:将其中一个图形绕着某一个点旋转180°能够与另一个图形重合 (全等图形不一定是中心对称的,而中心对称的两个图形一定是全等的) .
2.中心对称图形: 把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
要点诠释:(1)中心对称图形指的是一个图形;
(2)线段,平行四边形,圆等等都是中心对称图形.
要点三、平移、轴对称、旋转
平移、轴对称、旋转之间的对比
平移 轴对称 旋转
相同点 都是全等变换(合同变换),即变换前后的图形全等.
不
同
点 定义 把一个图形沿某一方向移动一定距离的图形变换. 把一个图形沿着某一条直线折叠的图形变换. 把一个图形绕着某一定点转动一个角度的图形变换.
图形
要素 平移方向
平移距离 对称轴 旋转中心、旋转方向、旋转角度
性质 连接各组对应点的线段平行(或共线)且相等. 任意一对对应点所连线段被对称轴垂直平分. 对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角都等于旋转角.
对应线段平行(或共线)且相等. 任意一对对应点所连线段被对称轴垂直平分. *对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角, 即:对应点与旋转中心连线所成的角彼此相等.
【典型例题】
类型一、旋转
1.如图1,ΔACB与ΔADE都是等腰直角三角形,∠ACB 和∠ADE都是直角,点C在AE上,如果ΔACB经逆时针旋转后能与ΔADE重合.
请指出其旋转中心与旋转角度;
②用图1作为基本图形,经过怎样的旋转可以得到图2?
【答案与解析】①旋转中心:点A; 旋转角度:45°(逆时针旋转)
②以点A为旋转中心,将图1顺时针(或逆时针)旋转90°三次得到图2.
【总结升华】此类题型要把握好旋转的三个要素:旋转中心、旋转方向和旋转角度.
举一反三:
【变式】如图,在平面直角坐标系中,△ABC和△DEF为等边三角形,AB=DE,点B、C、D在x轴上,点A、E、F在y轴上,下面判断正确的是( )
A.△DEF是△ABC绕点O顺时针旋转90°得到的.
B.△DEF是△ABC绕点O逆时针旋转90°得到的.
C.△DEF是△ABC绕点O顺时针旋转60°得到的.
D.△DEF是△ABC绕点O顺时针旋转120°得到的.
【答案】A.
类型二、中心对称
2. 如图,△ABC中A(-2,3),B(-3,1),C(-1,2).
⑴将△ABC向右平移4个单位长度,画出平移后的△A1B1C1;
⑵画出△ABC关于x轴对称的△A2B2C2;
⑶画出△ABC关于原点O对称的△A3B3C3;
⑷在△A1B1C1,△A2B2C2,△A3B3C3中,
△______与△______成轴对称,对称轴是______;
△______与△______成中心对称,对称中心的坐标是______.
【答案与解析】 ⑷△A2B2C2与△A3B3C3成轴对称,对称轴是y轴.
△A3B3C3与△A1B1C1成中心对称,对称中心的坐标是(2,0).
【总结升华】注意观察中心对称和旋转对称的关系.
举一反三:
【变式】如图是正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.
【答案】
类型三、平移、轴对称、旋转
3.如图所示,△ABC,△ADE为等腰直角三角形,∠ACB=∠AED=90°.
(1)如图1,点E在AB上,点D与C重合,F为线段BD的中点.则线段EF与FC的数量关系是 ;∠EFD的度数为 ;
(2)如图2,在图1的基础上,将△ADE绕A点顺时针旋转到如图2的位置,其中D、A、C在一条直线上,F为线段BD的中点.则线段EF与FC是否存在某种确定的数量关系和位置关系?证明你的结论;
(3)若△ADE绕A点任意旋转一个角度到如图③的位置,F为线段BD的中点,连接EF、FC,请你完成图3,并直接写出线段EF与FC的关系(无需证明).
【思路点拨】(1)易得△EFC是等腰直角三角形,那么EF=FC,∠EFD=90°.
(2)延长线段CF到M,使CF=FM,连接DM、ME、EC,易证△BFC≌△DFM,进而可以证明△MDE≌△CAE,即可证明EF=FC,EF⊥FC;
(3)基本方法同(2).
【答案与解析】解:(1)EF=FC,90°.
(2)延长CF到M,使CF=FM,连接DM、ME、EC,如下图2
∵FC=FM,∠BFC=∠DFM,DF=FB,
∴△BFC≌△DFM,
∴DM=BC,∠MDB=∠FBC,
∴MD=AC,MD∥BC,
∵ED=EA,∠MDE=∠EAC=135°,
∴△MDE≌△CAE,
∴ME=EC,∠DEM=∠CEA,
∴∠MEC=90°,
∴EF=FC,EF⊥FC
(3)图形如下,结论为:EF=FC,EF⊥FC.
【总结升华】延长过三角形的中线构造全等三角形是常用的辅助线方法,证明线段相等的问题可以转化为证明三角形全等的问题解决.
举一反三:
【变式】如图,△ABC中,∠BAC=90°,AC=2,AB=,△ACD是等边三角形.
(1)求∠ABC的度数.
(2)以点A为中心,把△ABD顺时针旋转60°,画出旋转后的图形.
(3)求BD的长度.
【答案】
(1)Rt△ABC中,AC=2,AB=,
∴BC=4,
∴∠ABC=30°
(2)如图所示:
(3)连接BE.
由(2)知:△ACE≌△ADB,
∴AE=AB,∠BAE=60°,BD=EC,
∴BE=AE=AB=,∠EBA=60°,
∴∠EBC=90°,
又BC=2AC=4,
∴Rt△EBC中,EC=
4.如图,Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CE=CF,EF交AC于G,连接AF.
(1)填空:线段BE、AF的数量关系为 ,位置关系为 ;
(2)当=时,求证:=2;
(3)若当=n时,=,请直接写出n的值.
【思路点拨】(1)在Rt△ABC中,AC=BC,∠ACB=90°,CF⊥CE,可推出∠ECB=∠ACF,且CE=CF,由此可得△ECB≌△FCA,即得BE=AF,∠CBE=∠CAF,且∠CBE+∠CAB=90°,故∠CAF+∠CAB=90°,即BE⊥AF;
(2)作GM⊥AB于M,GN⊥AF于N,可得出GM=GN,从而有S△AEG=2S△AFG,即证=2;
(3)根据(2)的推理过程,知S△AEG=nS△AFG,则,即可求得n的值.
【答案与解析】 (1)解:∵∠ACB=90°,CF⊥CE,
∴∠ECB=∠ACF.
又AC=BC,CE=CF,
∴△ECB≌△FCA.
∴BE=AF,∠CBE=∠CAF,
又∠CBE+∠CAB=90°,
∴∠CAF+∠CAB=90°,
即BE=AF,BE⊥AF.
(2)证明:作GM⊥AB于M,GN⊥AF于N,
∵△ACF可由△BCE绕点C顺时针方向旋转90°而得到,
∴AF=BE,∠CAF=∠CBE=45°.
∴AE=2AF,∠CAF=∠CAB,
∴GM=GN.
∴S△AEG=2S△AFG,
∴EG=2GF,
∴=2.
(3)解:由(2),得
当=n时,S△AEG=nS△AFG,
则,
∴当n=时,=.
【总结升华】此题综合运用了全等三角形的判定和性质、旋转的性质,能够从特殊推广到一般发现规律.
5.已知:点P是正方形ABCD内的一点,连结PA、PB、PC,
(1)若PA=2,PB=4,∠APB=135°,求PC的长.
(2)若,请说明点P必在对角线AC上.
【思路点拨】通过旋转,把PA、PB、PC或关联的线段集中到同一个三角形,再根据两边的平方和等于第三边求证直角三角形,可以求解∠APD.
【答案与解析】
(1)∵AB=BC,∠ABC=90°,
∴△CBP绕点B逆时针旋转90°,得到△ABE,
∵BC=BA,BP=BE,∠CBP=∠ABE
∴△CBP≌△ABE
∴AE=PC
∵BE=BP,∠PBE=90°,PB=4
∴∠BPE=45°,PE=
又∵∠APB=135°
∴∠APE=90°
∴
即AE=6,
所以PC=6.
(2)由(1)证得:PE=BP,PC=AE
∵
∴
∴∠PAE=90°
即∠PAB+∠BAE=90°
又∵由(1)证得∠BAE=∠BCP
∴∠PAB+∠BCP=90
又∵∠ABC=90°
∴点A,P,C三点共线,
即P必在对角线AC上.
【总结升华】注意勾股定理及逆定理的灵活运用.
举一反三:
【变式】如图,在四边形ABCD中,AB=BC,,K为AB上一点,N为BC上一点.若的周长等于AB的2倍,求的度数.
【答案】显然,绕点D顺时针方向旋转至
6如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得它们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、C、F、D在同一条直线上,且点C与点F重合(在图3~图6中统一用F表示)
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
⑴将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
⑵将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
⑶将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH.
【答案与解析】⑴平移的距离为5cm(即)
⑵
⑶证明:
在△AHE与△DHB1中
∴△AHE≌△DHB1(AAS) ∴AH=DH.
【总结升华】注意平移和旋转综合运用时找出不变量是解题的关键.
PAGE
《旋转》全章复习与巩固(提高)知识讲解
【知识网络】
【要点梳理】要点一、旋转
1. 旋转的概念:把一个图形绕着某一点O转动一个角度的图形变换叫做旋转..点O叫做旋转中心,转动的角叫做旋转角(如∠AO A′),如果图形上的点A经过旋转变为点A′,那么,这两个点叫做这个旋转的对应点.
要点诠释:旋转的三个要素:旋转中心、旋转方向和旋转角度.
2.旋转的性质: (1)对应点到旋转中心的距离相等(OA= OA′);
(2)对应点与旋转中心所连线段的夹角等于旋转角;
(3)旋转前、后的图形全等(△ABC≌△).
要点诠释:图形绕某一点旋转,既可以按顺时针旋转也可以按逆时针旋转.
3. 旋转的作图: 在画旋转图形时,首先确定旋转中心,其次确定图形的关键点,再将这些关键
沿指定的方向旋转指定的角度,然后连接对应的部分,形成相应的图形.
要点诠释:
作图的步骤:(1)连接图形中的每一个关键点与旋转中心;
(2)把连线按要求(顺时针或逆时针)绕旋转中心旋转一定的角度(旋转角);
(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;
(4)连接所得到的各对应点.
要点二、特殊的旋转—中心对称
1.中心对称: 把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.
要点诠释:(1)有两个图形,能够完全重合,即形状大小都相同;
(2)位置必须满足一个条件:将其中一个图形绕着某一个点旋转180°能够与另一个图形重合 (全等图形不一定是中心对称的,而中心对称的两个图形一定是全等的) .
2.中心对称图形: 把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
要点诠释:(1)中心对称图形指的是一个图形;
(2)线段,平行四边形,圆等等都是中心对称图形.
要点三、平移、轴对称、旋转
平移、轴对称、旋转之间的对比
平移 轴对称 旋转
相同点 都是全等变换(合同变换),即变换前后的图形全等.
不
同
点 定义 把一个图形沿某一方向移动一定距离的图形变换. 把一个图形沿着某一条直线折叠的图形变换. 把一个图形绕着某一定点转动一个角度的图形变换.
图形
要素 平移方向
平移距离 对称轴 旋转中心、旋转方向、旋转角度
性质 连接各组对应点的线段平行(或共线)且相等. 任意一对对应点所连线段被对称轴垂直平分. 对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角都等于旋转角.
对应线段平行(或共线)且相等. 任意一对对应点所连线段被对称轴垂直平分. *对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角, 即:对应点与旋转中心连线所成的角彼此相等.
【典型例题】
类型一、旋转
1.如图1,ΔACB与ΔADE都是等腰直角三角形,∠ACB 和∠ADE都是直角,点C在AE上,如果ΔACB经逆时针旋转后能与ΔADE重合.
请指出其旋转中心与旋转角度;
②用图1作为基本图形,经过怎样的旋转可以得到图2?
【答案与解析】①旋转中心:点A; 旋转角度:45°(逆时针旋转)
②以点A为旋转中心,将图1顺时针(或逆时针)旋转90°三次得到图2.
【总结升华】此类题型要把握好旋转的三个要素:旋转中心、旋转方向和旋转角度.
举一反三:
【变式】如图,在平面直角坐标系中,△ABC和△DEF为等边三角形,AB=DE,点B、C、D在x轴上,点A、E、F在y轴上,下面判断正确的是( )
A.△DEF是△ABC绕点O顺时针旋转90°得到的.
B.△DEF是△ABC绕点O逆时针旋转90°得到的.
C.△DEF是△ABC绕点O顺时针旋转60°得到的.
D.△DEF是△ABC绕点O顺时针旋转120°得到的.
【答案】A.
类型二、中心对称
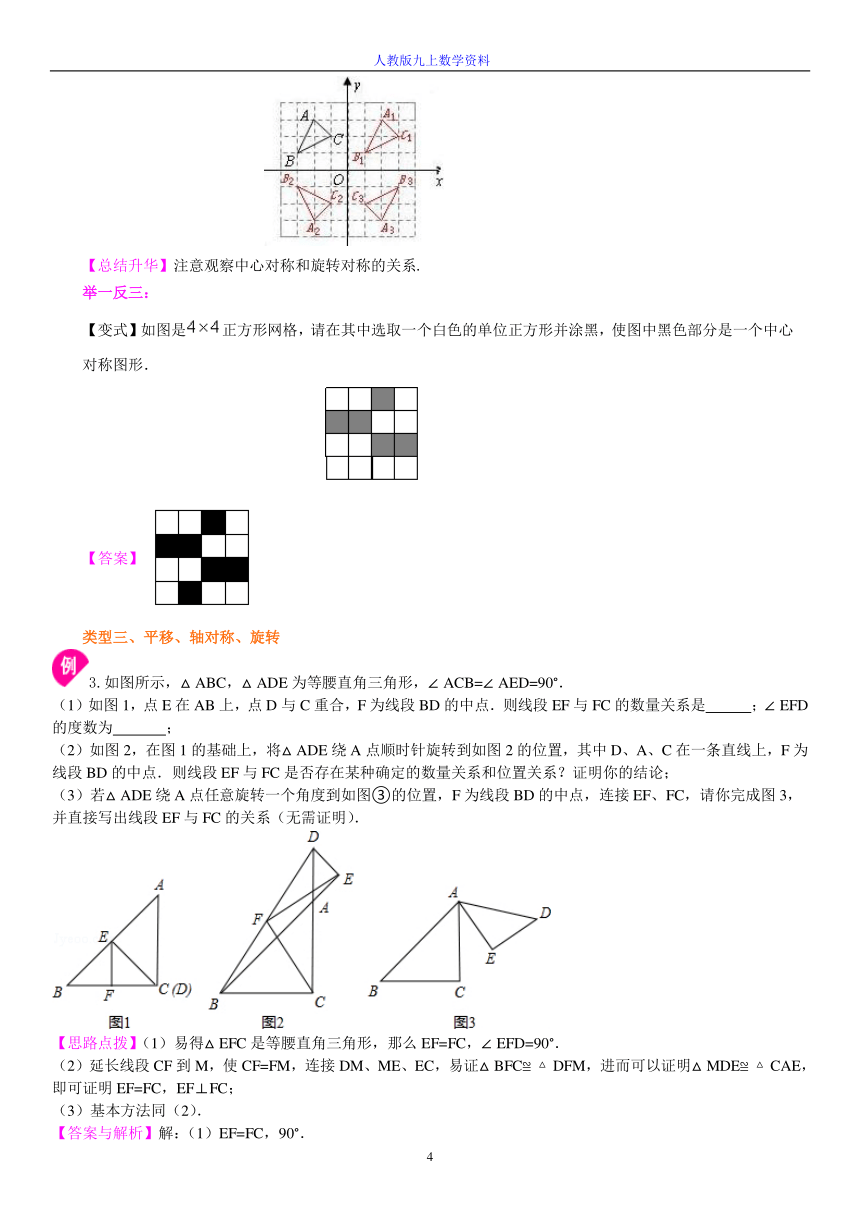
2. 如图,△ABC中A(-2,3),B(-3,1),C(-1,2).
⑴将△ABC向右平移4个单位长度,画出平移后的△A1B1C1;
⑵画出△ABC关于x轴对称的△A2B2C2;
⑶画出△ABC关于原点O对称的△A3B3C3;
⑷在△A1B1C1,△A2B2C2,△A3B3C3中,
△______与△______成轴对称,对称轴是______;
△______与△______成中心对称,对称中心的坐标是______.
【答案与解析】 ⑷△A2B2C2与△A3B3C3成轴对称,对称轴是y轴.
△A3B3C3与△A1B1C1成中心对称,对称中心的坐标是(2,0).
【总结升华】注意观察中心对称和旋转对称的关系.
举一反三:
【变式】如图是正方形网格,请在其中选取一个白色的单位正方形并涂黑,使图中黑色部分是一个中心对称图形.
【答案】
类型三、平移、轴对称、旋转
3.如图所示,△ABC,△ADE为等腰直角三角形,∠ACB=∠AED=90°.
(1)如图1,点E在AB上,点D与C重合,F为线段BD的中点.则线段EF与FC的数量关系是 ;∠EFD的度数为 ;
(2)如图2,在图1的基础上,将△ADE绕A点顺时针旋转到如图2的位置,其中D、A、C在一条直线上,F为线段BD的中点.则线段EF与FC是否存在某种确定的数量关系和位置关系?证明你的结论;
(3)若△ADE绕A点任意旋转一个角度到如图③的位置,F为线段BD的中点,连接EF、FC,请你完成图3,并直接写出线段EF与FC的关系(无需证明).
【思路点拨】(1)易得△EFC是等腰直角三角形,那么EF=FC,∠EFD=90°.
(2)延长线段CF到M,使CF=FM,连接DM、ME、EC,易证△BFC≌△DFM,进而可以证明△MDE≌△CAE,即可证明EF=FC,EF⊥FC;
(3)基本方法同(2).
【答案与解析】解:(1)EF=FC,90°.
(2)延长CF到M,使CF=FM,连接DM、ME、EC,如下图2
∵FC=FM,∠BFC=∠DFM,DF=FB,
∴△BFC≌△DFM,
∴DM=BC,∠MDB=∠FBC,
∴MD=AC,MD∥BC,
∵ED=EA,∠MDE=∠EAC=135°,
∴△MDE≌△CAE,
∴ME=EC,∠DEM=∠CEA,
∴∠MEC=90°,
∴EF=FC,EF⊥FC
(3)图形如下,结论为:EF=FC,EF⊥FC.
【总结升华】延长过三角形的中线构造全等三角形是常用的辅助线方法,证明线段相等的问题可以转化为证明三角形全等的问题解决.
举一反三:
【变式】如图,△ABC中,∠BAC=90°,AC=2,AB=,△ACD是等边三角形.
(1)求∠ABC的度数.
(2)以点A为中心,把△ABD顺时针旋转60°,画出旋转后的图形.
(3)求BD的长度.
【答案】
(1)Rt△ABC中,AC=2,AB=,
∴BC=4,
∴∠ABC=30°
(2)如图所示:
(3)连接BE.
由(2)知:△ACE≌△ADB,
∴AE=AB,∠BAE=60°,BD=EC,
∴BE=AE=AB=,∠EBA=60°,
∴∠EBC=90°,
又BC=2AC=4,
∴Rt△EBC中,EC=
4.如图,Rt△ABC中,AC=BC,∠ACB=90°,点E在线段AB上,CF⊥CE,CE=CF,EF交AC于G,连接AF.
(1)填空:线段BE、AF的数量关系为 ,位置关系为 ;
(2)当=时,求证:=2;
(3)若当=n时,=,请直接写出n的值.
【思路点拨】(1)在Rt△ABC中,AC=BC,∠ACB=90°,CF⊥CE,可推出∠ECB=∠ACF,且CE=CF,由此可得△ECB≌△FCA,即得BE=AF,∠CBE=∠CAF,且∠CBE+∠CAB=90°,故∠CAF+∠CAB=90°,即BE⊥AF;
(2)作GM⊥AB于M,GN⊥AF于N,可得出GM=GN,从而有S△AEG=2S△AFG,即证=2;
(3)根据(2)的推理过程,知S△AEG=nS△AFG,则,即可求得n的值.
【答案与解析】 (1)解:∵∠ACB=90°,CF⊥CE,
∴∠ECB=∠ACF.
又AC=BC,CE=CF,
∴△ECB≌△FCA.
∴BE=AF,∠CBE=∠CAF,
又∠CBE+∠CAB=90°,
∴∠CAF+∠CAB=90°,
即BE=AF,BE⊥AF.
(2)证明:作GM⊥AB于M,GN⊥AF于N,
∵△ACF可由△BCE绕点C顺时针方向旋转90°而得到,
∴AF=BE,∠CAF=∠CBE=45°.
∴AE=2AF,∠CAF=∠CAB,
∴GM=GN.
∴S△AEG=2S△AFG,
∴EG=2GF,
∴=2.
(3)解:由(2),得
当=n时,S△AEG=nS△AFG,
则,
∴当n=时,=.
【总结升华】此题综合运用了全等三角形的判定和性质、旋转的性质,能够从特殊推广到一般发现规律.
5.已知:点P是正方形ABCD内的一点,连结PA、PB、PC,
(1)若PA=2,PB=4,∠APB=135°,求PC的长.
(2)若,请说明点P必在对角线AC上.
【思路点拨】通过旋转,把PA、PB、PC或关联的线段集中到同一个三角形,再根据两边的平方和等于第三边求证直角三角形,可以求解∠APD.
【答案与解析】
(1)∵AB=BC,∠ABC=90°,
∴△CBP绕点B逆时针旋转90°,得到△ABE,
∵BC=BA,BP=BE,∠CBP=∠ABE
∴△CBP≌△ABE
∴AE=PC
∵BE=BP,∠PBE=90°,PB=4
∴∠BPE=45°,PE=
又∵∠APB=135°
∴∠APE=90°
∴
即AE=6,
所以PC=6.
(2)由(1)证得:PE=BP,PC=AE
∵
∴
∴∠PAE=90°
即∠PAB+∠BAE=90°
又∵由(1)证得∠BAE=∠BCP
∴∠PAB+∠BCP=90
又∵∠ABC=90°
∴点A,P,C三点共线,
即P必在对角线AC上.
【总结升华】注意勾股定理及逆定理的灵活运用.
举一反三:
【变式】如图,在四边形ABCD中,AB=BC,,K为AB上一点,N为BC上一点.若的周长等于AB的2倍,求的度数.
【答案】显然,绕点D顺时针方向旋转至
6如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得它们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、C、F、D在同一条直线上,且点C与点F重合(在图3~图6中统一用F表示)
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
⑴将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F 重合,请你求出平移的距离;
⑵将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
⑶将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH.
【答案与解析】⑴平移的距离为5cm(即)
⑵
⑶证明:
在△AHE与△DHB1中
∴△AHE≌△DHB1(AAS) ∴AH=DH.
【总结升华】注意平移和旋转综合运用时找出不变量是解题的关键.
PAGE
同课章节目录
