滁州市花山初级中学沪科版七年级数学下册6.2实数课件(共33张PPT)
文档属性
| 名称 | 滁州市花山初级中学沪科版七年级数学下册6.2实数课件(共33张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-06 00:00:00 | ||
图片预览







文档简介
课件33张PPT。6.2 实数 七(1)是我家,我爱我家!它们是正确的吗?
-4是16的平方根
16的平方根是4与-4
平方根等于本身的数1,0
算术平方根等于本身的数是1
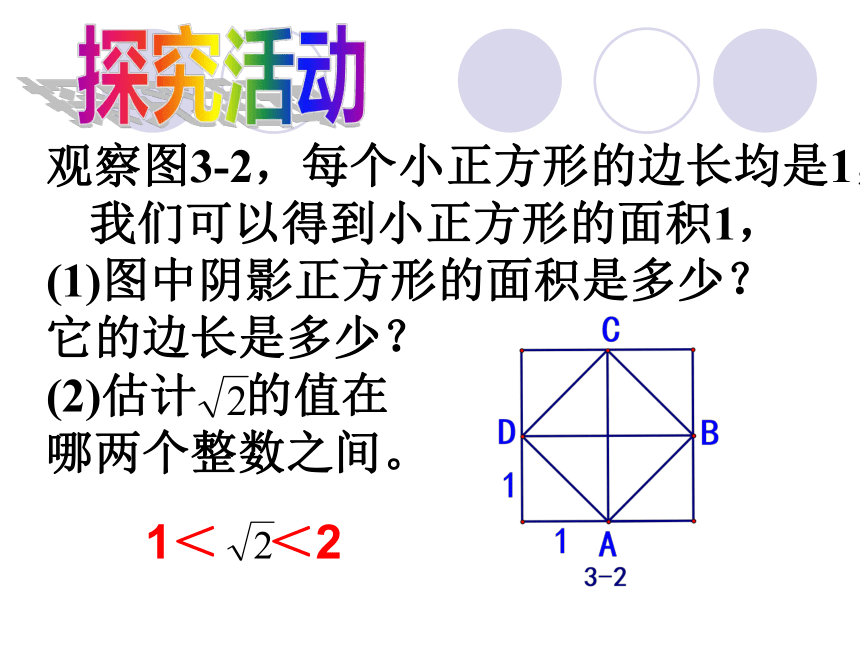
3的算术平方根记作观察图3-2,每个小正方形的边长均是1,我们可以得到小正方形的面积1,
(1)图中阴影正方形的面积是多少?
它的边长是多少?
(2)估计 的值在
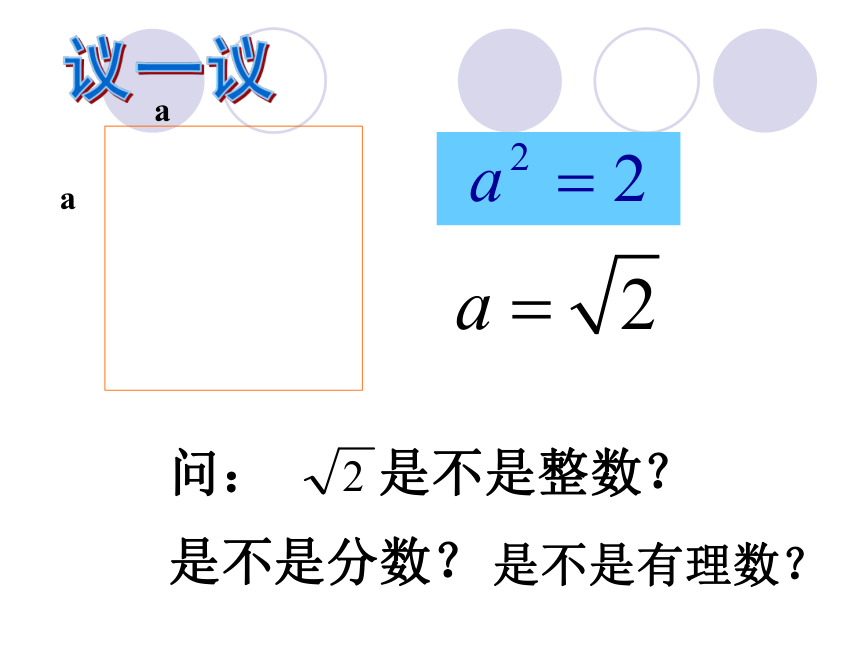
哪两个整数之间。 1< <2探究活动 是不是有理数?议一议aa问: 是不是整数?是不是分数?用这种方法可以得到一系列越来越接近
的 近似值。
=
1.414 213 562 373 095 048 801 688 724 209 6……我们把这种无限不循环小数叫做无理数。无理数的三种形式:
2 ). π, -π…3). 0.101001000…(两个“1”之间依次多一个0),
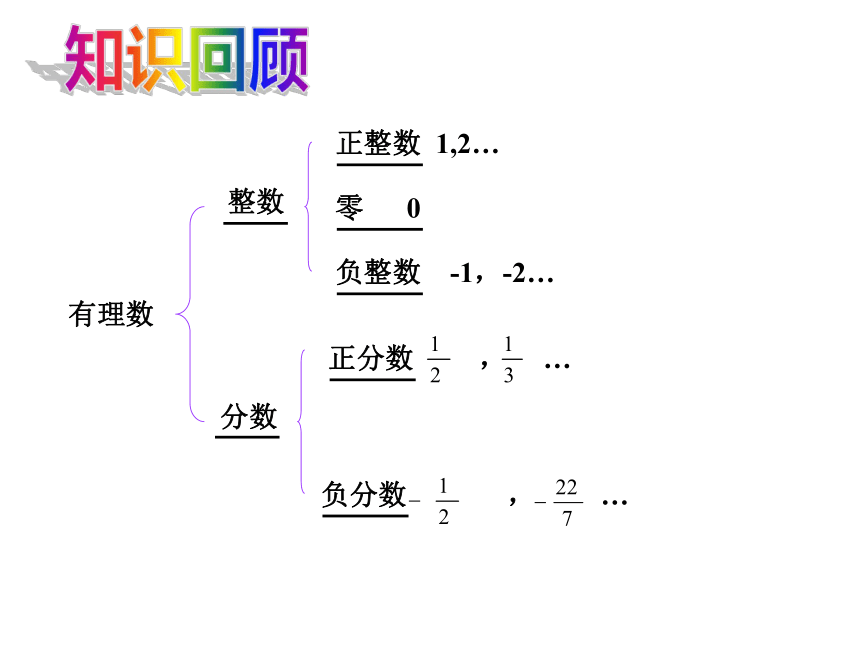
-7.2121121112… (两个“2”之间依次多一个1)有理数整数分数正整数 1,2… 零 0负整数 -1,-2… 负分数 , …知识回顾有理数还有分类方法吗?
有理数的分类:
正有理数
零
负有理数
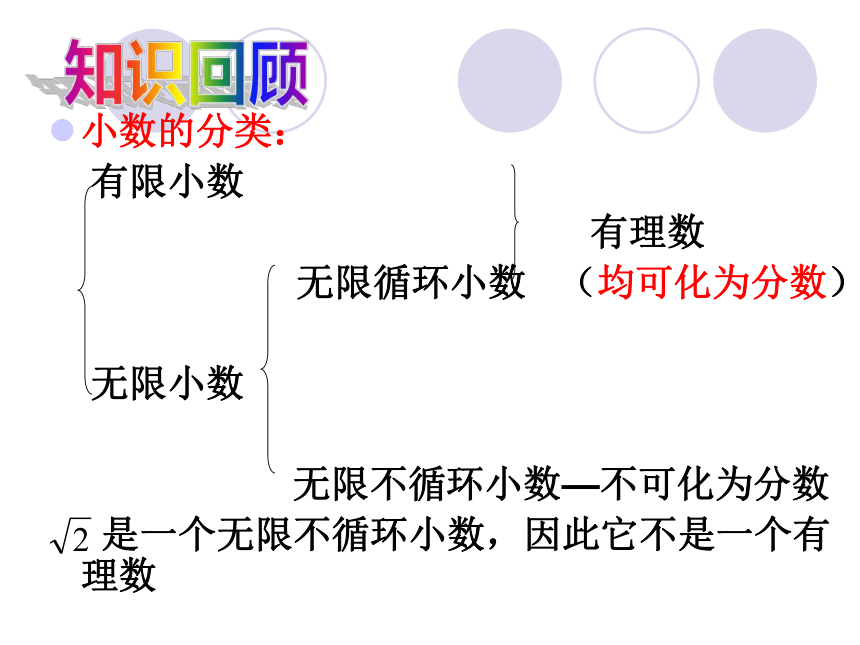
知识回顾小数的分类:
有限小数
有理数
无限循环小数 (均可化为分数)
无限小数
无限不循环小数—不可化为分数
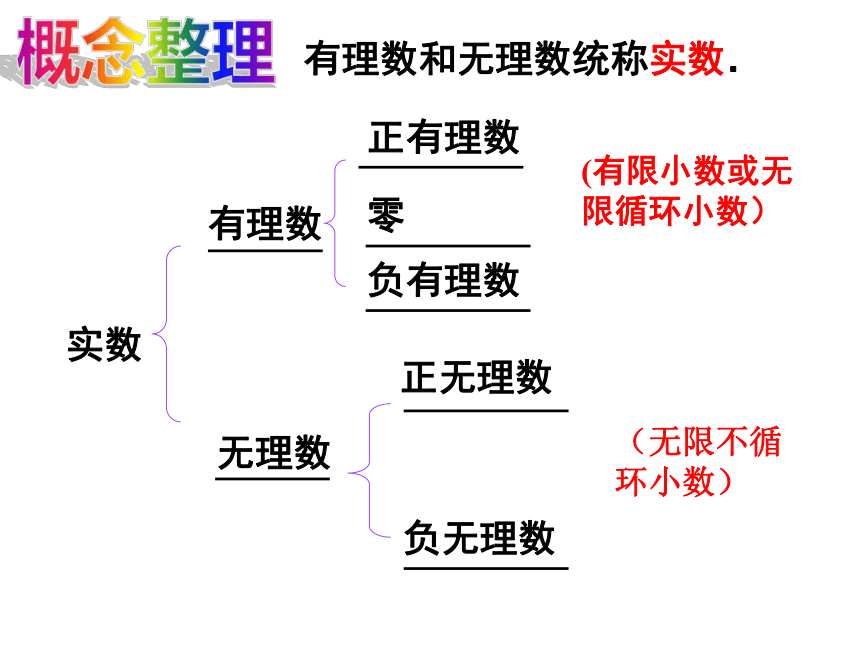
是一个无限不循环小数,因此它不是一个有理数知识回顾实数有理数无理数正有理数零负有理数正无理数负无理数有理数和无理数统称实数.(无限不循环小数)(有限小数或无限循环小数)概念整理1)在 中,属于有理数的:
属于无理数的:
属于实数的有:把数从有理数扩充到实数后,有理数的相反数和绝对值的概念同样适用于实数。∵
∴绝对值等于 的数是 和
例如: 和 互为相反数
填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________
5、一个数的绝对值是π,这个数是 ; ; ;实数轴按照昨天学过的知识,你能否想象出 在数轴上的位置吗?
你能想办法在数轴上找到 表示的点吗?
相关知识:正方形的面积=边长之积=对角线之积的一半单位正方形(边长为1的正方形)在数轴中找到
在数轴上作出 的对应点.0123-112012-1-2A一个实数a例:把下列实数表示在数轴上,并比较它们的
大小(用“<”号连接)解:在数轴上表示如下。由上图得,- <-1.4< <1.5<π<3.3 -2 -1 0 1 2 3 4 5····1.53.3··-1.4-2 -1 0 1 2 3 4 5试一试:
你能在数轴上表示出 吗?如果将所有的有理数都标到数轴上,那么数轴将被填满吗?
如果再将所有的无理数都标到数轴上,那么数轴被填满了吗?
总结:数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示。
即:实数与数轴上的点一一对应归纳整理让你的思维动起来想一想: 是有理数还是无理数?
判断:
带有根号的数一定是无理数( )
无理数一定含有根号( )
无限小数一定是无理数( )
无理数的绝对值一定是无理数 ( )
两无理数的和一定是无理数( )
两个无理数的积一定是无理数( )
有理数与数轴上的点一一对应( )×××××√×归纳总结谈一谈:本节课你有何收获?(1)无理数、实数的概念,实数的分类;
(2)知道实数与数轴上的点一一对应,能将实数表示在数轴上;
(3)相反数、绝对值、数的大小比较法则同样适用于实数. 小结: 实数的分类:
正有理数 整数 正有理数
正实数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负实数 无理数
负无理数 负无理数
(1)1.7 和
例:比较下列各组里两个数的大小.(2)布置作业1、草稿纸作业:课本第15页练习1 3 4习题1 3。
2、课堂作业:课本第16页2 4题。谢谢! 听一听ZLlb神奇的π祖冲之
(南北朝) 刘徽
(魏晋时期) 阿基米德(古希腊)神奇的π板书设计
-4是16的平方根
16的平方根是4与-4
平方根等于本身的数1,0
算术平方根等于本身的数是1
3的算术平方根记作观察图3-2,每个小正方形的边长均是1,我们可以得到小正方形的面积1,
(1)图中阴影正方形的面积是多少?
它的边长是多少?
(2)估计 的值在
哪两个整数之间。 1< <2探究活动 是不是有理数?议一议aa问: 是不是整数?是不是分数?用这种方法可以得到一系列越来越接近
的 近似值。
=
1.414 213 562 373 095 048 801 688 724 209 6……我们把这种无限不循环小数叫做无理数。无理数的三种形式:
2 ). π, -π…3). 0.101001000…(两个“1”之间依次多一个0),
-7.2121121112… (两个“2”之间依次多一个1)有理数整数分数正整数 1,2… 零 0负整数 -1,-2… 负分数 , …知识回顾有理数还有分类方法吗?
有理数的分类:
正有理数
零
负有理数
知识回顾小数的分类:
有限小数
有理数
无限循环小数 (均可化为分数)
无限小数
无限不循环小数—不可化为分数
是一个无限不循环小数,因此它不是一个有理数知识回顾实数有理数无理数正有理数零负有理数正无理数负无理数有理数和无理数统称实数.(无限不循环小数)(有限小数或无限循环小数)概念整理1)在 中,属于有理数的:
属于无理数的:
属于实数的有:把数从有理数扩充到实数后,有理数的相反数和绝对值的概念同样适用于实数。∵
∴绝对值等于 的数是 和
例如: 和 互为相反数
填空:
(1) 的相反数是__________
(2) 的相反数是
(3) ___________
(4)绝对值等于 的数是 _________
5、一个数的绝对值是π,这个数是 ; ; ;实数轴按照昨天学过的知识,你能否想象出 在数轴上的位置吗?
你能想办法在数轴上找到 表示的点吗?
相关知识:正方形的面积=边长之积=对角线之积的一半单位正方形(边长为1的正方形)在数轴中找到
在数轴上作出 的对应点.0123-112012-1-2A一个实数a例:把下列实数表示在数轴上,并比较它们的
大小(用“<”号连接)解:在数轴上表示如下。由上图得,- <-1.4< <1.5<π<3.3 -2 -1 0 1 2 3 4 5····1.53.3··-1.4-2 -1 0 1 2 3 4 5试一试:
你能在数轴上表示出 吗?如果将所有的有理数都标到数轴上,那么数轴将被填满吗?
如果再将所有的无理数都标到数轴上,那么数轴被填满了吗?
总结:数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示。
即:实数与数轴上的点一一对应归纳整理让你的思维动起来想一想: 是有理数还是无理数?
判断:
带有根号的数一定是无理数( )
无理数一定含有根号( )
无限小数一定是无理数( )
无理数的绝对值一定是无理数 ( )
两无理数的和一定是无理数( )
两个无理数的积一定是无理数( )
有理数与数轴上的点一一对应( )×××××√×归纳总结谈一谈:本节课你有何收获?(1)无理数、实数的概念,实数的分类;
(2)知道实数与数轴上的点一一对应,能将实数表示在数轴上;
(3)相反数、绝对值、数的大小比较法则同样适用于实数. 小结: 实数的分类:
正有理数 整数 正有理数
正实数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负实数 无理数
负无理数 负无理数
(1)1.7 和
例:比较下列各组里两个数的大小.(2)布置作业1、草稿纸作业:课本第15页练习1 3 4习题1 3。
2、课堂作业:课本第16页2 4题。谢谢! 听一听ZLlb神奇的π祖冲之
(南北朝) 刘徽
(魏晋时期) 阿基米德(古希腊)神奇的π板书设计
