第七单元扇形统计图情境化试题专练 (含答案)人教版数学六年级上册
文档属性
| 名称 | 第七单元扇形统计图情境化试题专练 (含答案)人教版数学六年级上册 |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 09:44:39 | ||
图片预览



文档简介
/ 让教学更有效
第七单元扇形统计图情境化专练
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.垃圾分类可减少污染,相关部门抽样调查了部分居民小区一段时间内垃圾分类情况,如果想清楚的看出每种生活垃圾占生活垃圾总量的百分比,选用( )比较合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.无法确定
2.美国人口仅占全球人口的3.5%(约3亿人),但排放的二氧化碳却占全球排放量的24%以上,是世界最大的温室气体排放国。因此,近年来,碳中和的呼声越来越高,各国相应出台了碳中和政策。下列说法错误的是( )。
A.美国每一亿人口碳排放量占全球排放量的8%。
B.美国每一亿人口碳排放量比中国每一亿人口碳排放量多。
C.中国碳排放量是美国的
D.美国与欧盟的碳排放量之和比其他国家排放量之和(不包含中国)都多。
3.地球陆地共分为七个大洲,即亚洲、欧洲、非洲、北美洲、南美洲、大洋洲和南极洲。下图是地球陆地面积分布统计图。根据图中的信息进行判断,关于七个大洲面积之间的关系,以下说法错误的是( )。
在七个大洲中,亚洲面积最大
B.北美洲的面积比南美洲的面积大
和欧洲面积最接近的是大洋洲的面积
D.亚洲与非洲的面积之和大于地球陆地总面积的50%
4.2023年10月8日晚,第19届亚运会在中国杭州圆满闭幕。在本届亚运会上,中国体育代表团再次展现了出色的体育实力。下面是本届亚运会中国体育代表团所获奖牌情况。
金牌 银牌 铜牌
数量/枚 201 111 71
约占本届亚运会中国体育代表团所获奖牌总数的百分比 52.5% 29.0% 18.5%
如果要用统计图清楚地表示金、银、铜牌占本届亚运会中国体育代表团所获奖牌总数的百分比,选择( )比较合适。
A.扇形统计图 B.条形统计图 C.折线统计图 D.复式折线统计图
5.为选拔更出色的运动员参加2024年巴黎奥运会,国家队从近3年就开始为每个队员绘制( ),来表示运动员们参加每次比赛成绩高低的变化。
A.条形统计图 B.折线统计图 C.扇形统计图 D.都不是
二、填空题
6.下图是第29届奥运会中国奖牌情况统计图。
(1)( )项目奖牌数最多,占奖牌总数的( )。( )项目的奖牌数最少,占奖牌总数的( )。
(2)( )和( )项目奖牌数等于( )项目的奖牌数。
(3)第29届奥运会中国奖牌总数为100枚,射击和体操一共获得了( )枚奖牌,占总奖牌数的( )。
7.“直播带货”已成为促进地区经济、文化发展的有效途径。2023年5月20日-5月25日,农产品直播电商平台“东方甄选”在太原古县城举办山西专场。短短6天,全国人民的热切目光对焦山西、上亿元的山西好物销往全国……据统计:此次“东方甄选山西行”销售“山西好物”约达130000000元,此前,仅一条宣传短视频就获得289000的点赞量。130000000读作( ),改写成用“亿”作单位的数是( );289000精确到万位是( )。如果把这6天每天的销售额占总销售额的百分比用统计图表示出来,最适宜选用( )统计图。(填“条形”“扇形”或“折线”)
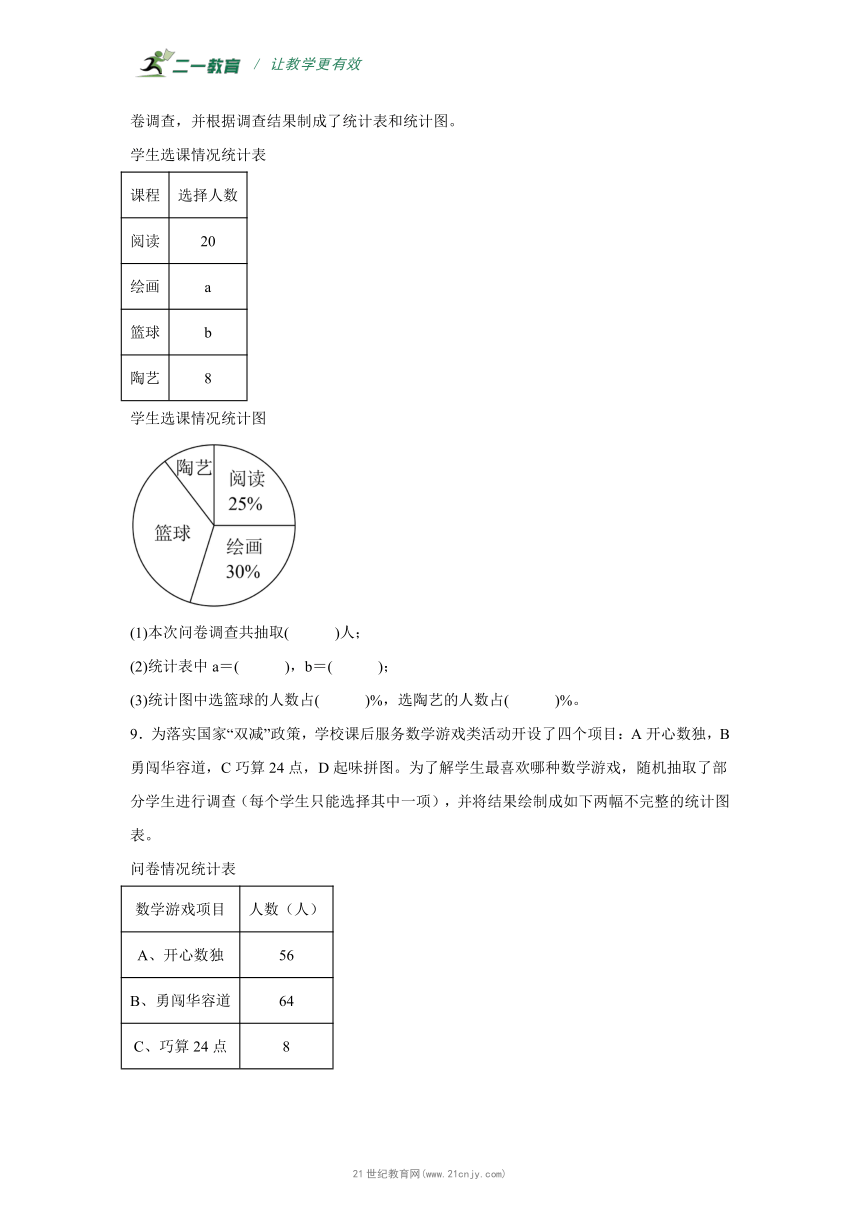
8.复兴小学一、二年级课后服务开设了阅读、绘画、羽毛球、陶艺四门兴趣课程,要求学生每人选择一门课程参加活动。为了了解学生的选课情况,学校随机抽取了部分学生进行问卷调查,并根据调查结果制成了统计表和统计图。
学生选课情况统计表
课程 选择人数
阅读 20
绘画 a
篮球 b
陶艺 8
学生选课情况统计图
(1)本次问卷调查共抽取( )人;
(2)统计表中a=( ),b=( );
(3)统计图中选篮球的人数占( )%,选陶艺的人数占( )%。
9.为落实国家“双减”政策,学校课后服务数学游戏类活动开设了四个项目:A开心数独,B勇闯华容道,C巧算24点,D起味拼图。为了解学生最喜欢哪种数学游戏,随机抽取了部分学生进行调查(每个学生只能选择其中一项),并将结果绘制成如下两幅不完整的统计图表。
问卷情况统计表
数学游戏项目 人数(人)
A、开心数独 56
B、勇闯华容道 64
C、巧算24点 8
D、趣味拼图
(1)本次一共调查了( )个学生,统计表中( )。
(2)若该校有2000名学生,请你估计该校最喜欢“C巧算24点”的学生约有( )人。
三、作图题
10.春峰小学2024年春季学期开展了“我最喜欢的实践活动场馆”调研,各年级学生参与调研的情况统计如表:
博物馆类 科技馆类 游艺场馆类 其它场馆
一年级 5 15 30 9
二年级 8 15 28 11
三年级 6 32 22 7
四年级 10 41 12 5
五年级 13 40 10 4
六年级 18 45 8 6
合计 60 188 110 42
(1)如图是军军同学对此次调研“最喜欢的实践活动场馆”情况进行整体分析后制作的部分统计图,请你继续完成统计图。
(2)根据统计图表,比较各年级“最喜欢科技类场馆”的情况,在括号写出你对调研结果的看法( )。
四、解答题
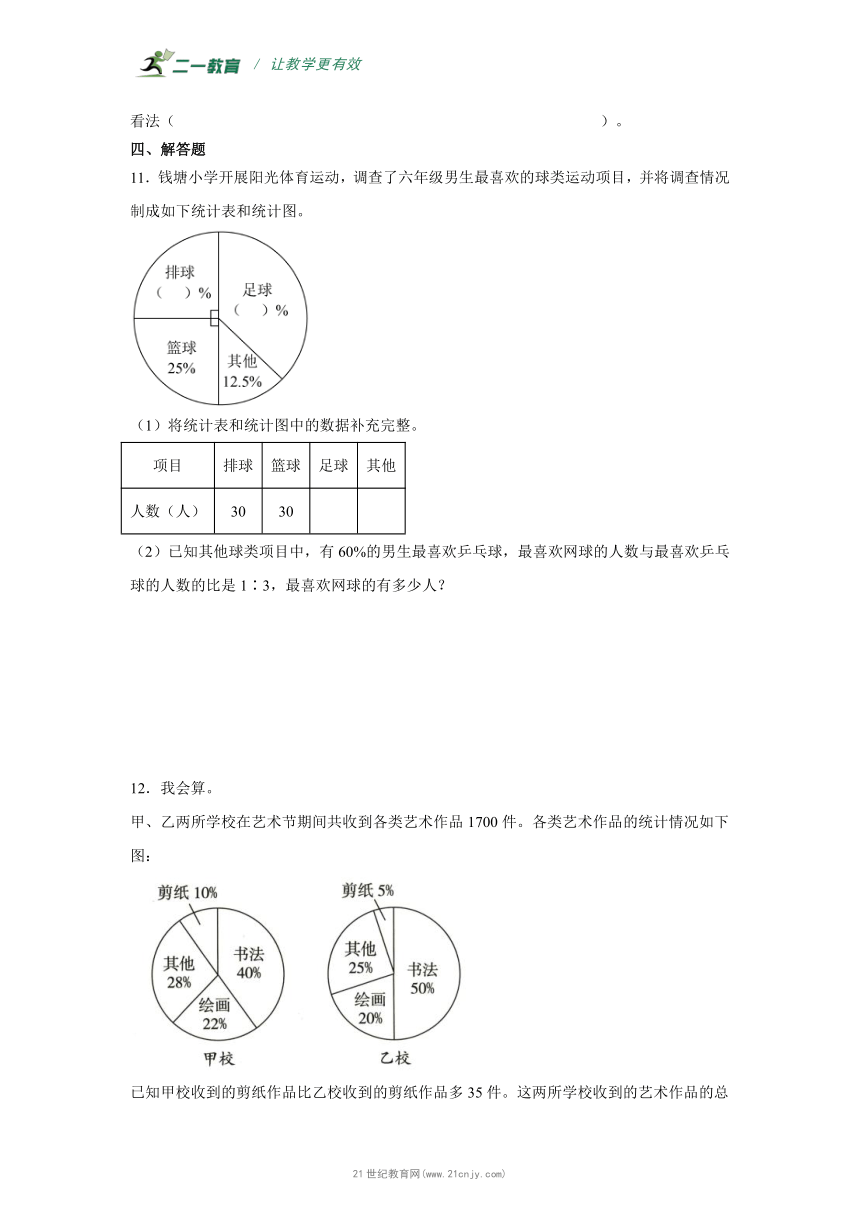
11.钱塘小学开展阳光体育运动,调查了六年级男生最喜欢的球类运动项目,并将调查情况制成如下统计表和统计图。
(1)将统计表和统计图中的数据补充完整。
项目 排球 篮球 足球 其他
人数(人) 30 30
(2)已知其他球类项目中,有60%的男生最喜欢乒乓球,最喜欢网球的人数与最喜欢乒乓球的人数的比是1∶3,最喜欢网球的有多少人?
12.我会算。
甲、乙两所学校在艺术节期间共收到各类艺术作品1700件。各类艺术作品的统计情况如下图:
已知甲校收到的剪纸作品比乙校收到的剪纸作品多35件。这两所学校收到的艺术作品的总数分别是多少件?
13.在习总书记“既要金山银山,又要绿水青山”思想的指导下,我国雾霾天气得到了较大改善,某校在学生中做了一次对雾霾知识了解程度的抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解。根据调查结果,绘制了如图所示的不完整的统计图。结合统计图,回答下列问题:
(1)本次参与调查的学生一共有( )人。
(2)“基本了解”的同学占( )。
(3)参与调查的学生中对雾霾情况“非常了解”的人数比“比较了解”的人数少百分之几?
14.对于电动自行车管理问题,《北京市单位消防安全主体责任规定》要求,单位设置的电动自行车停放场所应当符合有关技术标准规定的防火间距、防火分区、充电设施等要求。同时,从严规定了电动自行车禁止入楼的要求,即“制止在建筑物内违规停放电动自行车或者为电动自行车充电的行为”。就这个问题,明明查阅资料了解相关信息如下:
资料一:
今年3月我市共发生电动自行车火灾35起,起火地点均为室外。
(1)请将扇形统计图和条形统计图分别补充完整。
(2)今年3月我市发生电动自行车火灾中,处于停放状态有( )起。
资料二:
电动自行车起火危害极其严重,主要包括:火场高温、有毒烟气的产生、电池爆炸以及救援困难等。
(3)根据明明所查数据和信息,请分析我市“电动自行车禁止入楼”的要求的合理性,写出你的理由。
15.如图是对部分六年级同学进行的“你最喜欢的一种球类运动”问卷调查统计情况,认真读图,完成下列问题。
(1)这是一个( )统计图。
(2)如果最喜欢打排球的有36人,那么这次问卷活动调查了( )人。
(3)根据(2)题的结论,有( )人最喜欢踢足球。
16.山西文旅集团推出五条旅游研学线路(如图):某校为了了解学生对哪条研学线路最感兴趣,从该校六年级学生中随机抽取了若干名学生进行调查,绘制了如图所示的条形统计图和扇形统计图。
请根据以上信息,解答下列问题:
(1)本次参与调查的学生共有多少名?
(2)请将条形统计图补充完整。
(3)在扇形统计图中,E所在的圆心角的度数是( )°。
(4)如果该校六年级共有学生480人,请你估计选择“D游山西,读汇通天下晋商史”的有( )人。
17.王老师对300名五年级学生的课外阅读情况进行调查,绘制了如图统计图。
(1)调查的五年级学生中,从不阅读课外书籍的同学有( )人。
(2)根据题目中的数据,把条形统计图补充完整。
(3)阅读《西游记》的人数大约比阅读《三国演义》的人数多( )。
18.为了弘扬中华优秀传统文化,某市举办了“典籍里的中国”中华经典诵读活动,下图是各个组别参赛作品数量情况统计图。
(1)中学组有64篇参赛作品,本次活动一共有( )篇参赛作品。
(2)教师组参赛作品的数量与小学组参赛作品的数量的比是( )。
(3)社会组有( )篇参赛作品。
19.在“2023年打击电信网络诈骗犯罪行动”中,我国有23个部门和单位联手打击显成效。学校开展“防止电信网络诈骗”的调查活动。同学们将调查结果整理分析后,正在绘制统计图。
(1)学校共调查了( )人。
(2)请将两幅统计图补充完整。
(3)防止网络诈骗,你想对你身边的人说些什么?
20.向阳社区开展防范电信诈骗宣传教育活动,进行了防止“电信网络诈骗”的调查活动,选择“你觉得最容易上当的诈骗方式”,并且每人只能选一项。工作人员将调查结果整理后,绘制了两副不完整的统计图(下图),请根据图中信息按要求作答。
(1)和平社区工作人员一共调查了( )人。
(2)把两个统计图补充完整,其中条形统计图的每个条形上方标注数据。
(3)你有什么防止电信诈骗的秘籍给同学们分享一下?
21.巩义市某小学5月份进行“数学文化节”活动(每人参加一个项目)。六年级学生参加项目信息如下:
项目 数学口算 数学阅读 汉诺塔 索玛立方体 数独
人数 132人 人 36人 24人 36人
①根据统计表和统计图中的信息,请你算出参加“数学文化节”的一共有多少人?
②请把统计表和统计图内信息补充完整。
③请提一个数学问题,并解答。
22.2024年4月23日“世界读书日”发布了《中国少年儿童阅读素养调查研究报告》,参与调查问卷的少年儿童约12万人。以下选取了其中部分统计信息:
(1)平均每天阅读时间在30分钟及以上的有多少万人?
(2)2023年中国少年儿童人均阅读量是11.4本,比2018年增长百分之几?(百分号前保留一位小数)
(3)请你选择相关信息提出一个数学问题,并解决。
参考答案:
1.C
【分析】条形统计图可以清晰反映数据情况,折线统计图可以反映数据的变化情况,扇形统计图可反映部分占整体的百分比情况。据此解题。
【详解】如果想清楚的看出每种生活垃圾占生活垃圾总量的百分比,选用扇形统计图比较合适。
故答案为:C
2.C
【分析】A.将二氧化碳全球排放量看作单位“1”,美国约3亿人,美国二氧化碳排放量对应百分率÷3=美国每一亿人口碳排放量占全球排放量的百分之几;
B.中国约14亿人,中国二氧化碳排放量对应百分率÷14=中国每一亿人口碳排放量占全球排放量的百分之几,与美国每一亿人口碳排放量占全球排放量的百分之几比较即可。
C.将美国碳排放量看作单位“1”,中国碳排放量对应百分率÷美国碳排放量对应百分率=中国碳排放量是美国的几分之几;
D.将美国的碳排放量对应百分率与欧盟的碳排放量对应百分率相加,与其他国家排放量对应百分率比较即可。
【详解】A.24%÷3=8%
美国每一亿人口碳排放量占全球排放量的8%,说法正确;
B.28%÷14=2%
8%>2%,美国每一亿人口碳排放量比中国每一亿人口碳排放量多,说法正确;
C.28%÷24%==
中国碳排放量是美国的,选项说法错误;
D.24%+13%=37%
37%>35%
美国与欧盟的碳排放量之和比其他国家排放量之和(不包含中国)都多,说法正确。
说法错误的是中国碳排放量是美国的。
故答案为:C
3.D
【分析】根据扇形统计图中的信息,比较七个大洲面积之间的大小,逐项分析,进行判断。
【详解】A.29.4>20.2%>16.2%>12%>9.4%>6.8%>6%,在七个大洲中,亚洲面积最大,原题说法正确;
B.16.2%>12%,北美洲的面积比南美洲的面积大,原题说法正确;
C.6.8%与6%最接近,和欧洲面积最接近的是大洋洲的面积,原题说法正确;
D.29.4%+20.2%=49.6%,49.6<50%,亚洲与非洲的面积之和小于地球陆地总面积的50%,原题说法错误。
故答案为:D
4.A
【分析】条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
扇形统计图表示各部分数量与总数之间的关系。
【详解】如果要用统计图清楚地表示金、银、铜牌占本届亚运会中国体育代表团所获奖牌总数的百分比,选择扇形统计图比较合适。
故答案为:A
5.B
【分析】用统计图表示数据时,要根据实际情况选择合适的统计图:(1)要表示出各种数量的多少时,选择条形统计图;(2)既要表示出各种数量的多少,又要表示出数量增减变化的情况时,选择折线统计图;(3)要表示出各部分数量与总数之间的关系时,选择扇形统计图。
【详解】国家队即要了解运动员们3年来参加每次比赛的具体成绩,又要了解成绩的增减变化趋势,所以,国家队从近3年就开始为每个队员绘制折线统计图,来表示运动员们参加每次比赛成绩高低的变化。
故答案为:B
6.(1) 水上 23% 田径 2%
(2) 球类 田径 水上
(3) 29 29%
【分析】(1)比较各项目奖牌数占奖牌总数的百分比即可。
(2)从统计图中找出哪两个项目的奖牌数占奖牌总数的百分比的和等于另一个项目的奖牌数占奖牌总数的百分比即可。
(3)把第29届奥运会中国奖牌总数看作单位“1”,从统计图中可知,射击和体操的奖牌数一共占奖牌总数的(11%+18%),单位“1”已知,用奖牌总数乘(11%+18%),即可求出射击和体操一共获得奖牌的数量。
【详解】(1)23%>22%>21%>18%>11%>3%>2%
(水上)项目奖牌数最多,占奖牌总数的(23%)。(田径)项目的奖牌数最少,占奖牌总数的(2%)。
(2)21%+2%=23%
或18%+3%=21%
(球类)和(田径)项目奖牌数等于(水上)项目的奖牌数。
或(体操)和(其它)项目奖牌数等于(球类)项目的奖牌数。
(3)11%+18%=29%
100×29%
=100×0.29
=29(枚)
第29届奥运会中国奖牌总数为100枚,射击和体操一共获得了(29)枚奖牌,占总奖牌数的(29%)。
7. 一亿三千万 1.3亿 29万 扇形
【分析】整数的读法是从高位到低位,一级一级地读。读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零,据此读出此数;
改写成用“亿”作单位的数,就在亿位的右下角点上小数点,同时小数末尾的0去掉,并在后面加个“亿”字;精确到万位,则看千位上的数,如果千位上的数大于等于5,则进一,小于5,则舍去,后面加个“万”字;
根据统计图的特点:折线统计图可以清楚的观察数量的增减变化情况;条形统计图可以清晰的看出数量的多少;扇形统计图可以反应部分与整体之间的关系,据此即可选择。
【详解】由分析可知:
130000000读作:一亿三千万,改写成用“亿”作单位的数是1.3亿,289000精确到万位是29万。如果把这6天每天的销售额占总销售额的百分比用统计图表示出来,最适宜选用扇形统计图。
8.(1)80
(2) 24 28
(3) 35 10
【分析】(1)用选阅读的人数除以阅读人数占的百分率,即可求出一共抽取的人数;
(2)用一共抽取的人数乘绘画人数占的百分率,即可求出选绘画的人数,再用抽取的总人数减去选阅读、绘画、陶艺的人数即可求出选篮球的人数;
(3)用选篮球的人数除以抽取的总人数,求出选篮球的人数占的百分率;同理用选陶艺的人数除以抽取的总人数,求出选陶艺的人数占的百分率。
【详解】(1)抽取人数:(人)
(2)a
b
(3)选篮球的人数占总人数的:
选陶艺的人数占总人数的:
【点睛】本题查扇形统计图的应用,能够根据统计图表提供的信息,解决有关的实际问题,是解题的关键。
9.(1) 160 32
(2)100
【分析】(1)观察统计图表,根据项有56人,项占总人数的,用A项的人数除以A项占总人数的百分率,求出调查的总人数;再用总人数减去A、B和C三项人数,即可得出趣味拼图人数;
(2)用调查的统计图表的数据计算估计:调查的人数中,开心数独项目有56人,巧算24点有8人,占开心数独的,即相当于总数的的;也就是总数的,据此可估算出喜欢巧算24点的学生约有多少人。
【详解】(1)(人)
(人)
本次一共调查了160个学生,统计表中的等于32。
(2)
(人)
按调查数据推算,若该校有2000名学生,该校最喜欢“巧算24点”的学生约有100人。
10.(1)见详解
(2)见详解
【分析】(1)根据调研情况统计表分别计算出博物馆类、科技馆类、游艺场馆类、其他场馆占全部调研情况的占比后绘制扇形统计图即可;
(2)分别计算出每个年级“最喜欢科技类场馆”的占比情况后发表看法(答案不唯一,合理即可)。
【详解】(1)60+188+110+42=400(人)
博物馆类:60÷400=15%
科技馆类:188÷400=47%
游艺场馆类:110÷400=27.5%
其它场馆:42÷400=10.5%
47%>27.5%>15%>10.5%
完成的统计图,如图:
(2)一年级科技馆类:
15÷(5+15+30+9)
=15÷59
≈25.4%
二年级科技馆类:
15÷(8+15+28+11)
=15÷62
≈24.2%
三年级科技馆类:
32÷(6+32+22+7)
=32÷67
≈47.8%
四年级科技馆类:
41÷(10+41+12+5)
=41÷68
≈60.3%
五年级科技馆类:
40÷(13+40+10+4)
=40÷67
≈59.7%
六年级科技馆类:
45÷(18+45+8+6)
=45÷77
≈58.4%
60.3%>59.7%>58.4%>47.8%>25.4%>24.2%
因此可得,四年级“最喜欢科技类场馆”的占比最高。(答案不唯一)
11.(1)见详解;
(2)3人
【分析】(1)将男生总人数看作单位“1”,观察扇形统计图可知,喜欢排球的人数是总人数的25%,1-喜欢篮球的对应百分率-喜欢排球的对应百分率-喜欢其他的对应百分率=喜欢足球的对应百分率;喜欢排球的人数÷对应百分率=总人数,总人数×喜欢足球的对应百分率=喜欢足球的人数,总人数×喜欢其他的对应百分率=喜欢其他的人数,据此求出相关数据,补充统计表和统计图即可;
(2)将喜欢其他球类的人数看作单位“1”,喜欢其他球类的人数×最喜欢乒乓球的人数对应百分率=最喜欢乒乓球的人数,将比的前后项看成份数,最喜欢乒乓球的人数÷对应份数=一份数,一份数×最喜欢网球的对应份数=最喜欢网球的人数。
【详解】(1)1-25%-25%-12.5%=37.5%
30÷25%=30÷0.25=120(人)
120×37.5%=120×0.375=45(人)
120×12.5%=120×0.125=15(人)
项目 排球 篮球 足球 其他
人数(人) 30 30 45 15
(2)15×60%
=15×0.6
=9(人)
9÷3×1=3(人)
答:最喜欢网球的有3人。
12.800件;900件
【分析】观察统计 图可知,甲校剪纸作品占10%,乙校剪纸作品占5%。又知甲、乙两所学校共收到各类艺术作品1700件,甲校收到的剪纸作品比乙校收到的剪纸作品多35件。可列方程解答,设甲校收到x件艺术作品,则乙校收到(1700-x)件艺术作品。甲校的剪纸作品有10%x件,乙校的剪纸作品有(1700-x)×5%件,所以10%x-(1700-x)×5%=35,解此方程求出甲校收到的艺术作品件数,进而求出乙校收到的艺术作品件数。
【详解】解:设甲校收到艺术作品的总数是x件。
10%x-(1700-x)×5%=35
10%x-85+5%x=35
15%x-85=35
15%x-85+85=35+85
15%x=120
15%x÷15%=120÷15%
x=800
乙校:1700-800=900(件)
答:甲校收到艺术作品800件,乙校收到艺术作品900件。
13.(1)400
(2)40
(3)75%
【分析】(1)把调查的学生总人数看作单位“1”,根据条形统计图和扇形统计图可知,“非常了解”的人数占调查的学生总人数的5%,对应的是20人,求单位“1”,用20÷5%解答;
(2)“基本了解”的人数÷调查的学生总人数×100%,即可求出“基本了解”的同学占调查学生人数的百分比;
(3)把“比较了解”的人数看作单位“1”,用非常了解”的人数与“比较了解”的人数差,除以“比较了解”的人数,再乘100%,即可解答。
【详解】(1)20÷5%=400(人)
本次参与调查的学生一共有400人。
(2)160÷400×100%
=0.4×100%
=40%
“基本了解”的同学占40%。
(3)(80-20)÷80×100%
=60÷80×100%
=0.75×100%
=75%
答:参与调查的学生中对雾霾情况“非常了解”的人数比“比较了解”的人数少75%。
14.(1)见详解
(2)26
(3)见详解
【分析】(1)电动车起火时状态为行驶状态和停放状态,根据扇形统计图可知,停放状态时起火占比为74.3%,则行驶状态时起火占比为1-74.3%=25.7%;根据北京市3月份起火数量35起可知,电池故障原因起火23起,其他原因起火4起,则线路故障起火为35-23-4=8起,据此完成统计图的绘制;
(2)求一个数的百分之几是多少,用乘法计算,用起火数量乘停放状态起火占起火数量的百分
数即可求解;
(3)根据统计的结果,说明电动车进楼的危害即可。
【详解】(1)1-74.3%=25.7%
35-23-4
=12-4
=8(起)
如图所示:
(2)35×74.3%≈26(起)
则今年3月我市发生电动自行车火灾中,处于停放状态有26起。
(3)电动自行车进楼容易引发火灾,造成重大事故;堵塞楼道,埋下安全隐患;加速电梯损坏,带来运行风险。
15.(1)扇形
(2)200
(3)48
【分析】(1)扇形统计图:用整圆表示总数,各扇形表示部分占总数的百分比,能直观体现部分与总数的关系,扇形大小反映占比大小。
(2)已知最喜欢打排球的人数占比为18%,人数为36人。用最喜欢打排球的人数除以其占总人数的百分比,即可得到总人数。
(3)已知总人数和最喜欢踢足球的人数占比为24%。用总人数乘最喜欢踢足球的人数占比,就能得出最喜欢踢足球的人数。
【详解】(1)综上分析所述,这是一个扇形统计图。
(2)因为最喜欢打排球的人数占总人数的18%,且最喜欢打排球的有36人,所以总人数为:36÷18%=36÷0.18=200(人)
那么这次问卷活动调查了200人。
(3)因为最喜欢踢足球的人数占总人数的24%,总人数为200人,所以最喜欢踢足球的人数为:200×24%=200×0.24=48(人)
有48人最喜欢踢足球。
16.(1)80名
(2)见详解
(3)90
(4)102
【分析】(1)由题意可知,对A路线感兴趣的学生有16人,占总人数的20%,根据已知一个数的百分之几是多少,求这个数,用除法计算,即用16除以20%即可;
(2)用总人数分别减去对A、B、C、E路线感兴趣的人数即可求出对D感兴趣的人数,进而完成条形统计图即可;
(3)用选择用E的人数除以总人数,化为分数形式,再根据分数的基本性质化为分母为360的分数即可;
(4)先求出选择D游山西的人数占总人数的分率,再根据求一个数的几分之几是多少,用乘法计算即可。
【详解】(1)16÷20%=80(名)
答:本次参与调查的学生共有80名。
(2)80-16-13-14-20
=64-13-14-20
=51-14-20
=37-20
=17(名)
如图所示:
(3)20÷80=
在扇形统计图中,E所在的圆心角的度数是90°。
(4)17÷80=
480×=102(人)
则选择“D游山西,读汇通天下晋商史”的有102人。
17.(1)30
(2)见详解
(3)23.1
【分析】(1)由题意可知,被调查的300名五年级学生中有10%的学生从不阅读,根据求一个数的百分之几是多少,用乘法解答,用300乘10%即可解答。
(2)把被调查的300名五年级学生看作单位“1”,用“1”减去偶尔阅读、从不阅读的学生占单位“1”的百分率的和,求出经常阅读的学生占总数的百分率,再根据求一个数的百分之几是多少,用乘法解答求出经常阅读的人数,再用经常阅读的人数减去阅读其它三种图书的人数和,求出阅读《水浒传》的人数,据此数据完成条形统计图。
(3)根据求一个数比另一个数多百分之几,用两个数的差除以另一个数解答即可。
【详解】(1)300×10%=30(人)
所以从不阅读的同学有30人。
(2)1-(10%+20%)
=1-30%
=70%
300×70%-(80+18+65)
=210-(98+65)
=210-163
=47(人)
如下图:
(3)(80-65)÷65
=15÷65
≈23.1%
答:阅读《西游记》的人数大约比阅读《三国演义》的人数多23.1%。
18.(1)200
(2)1∶2
(3)16
【分析】(1)把参赛作品的总数看作单位“1”,中学组参赛作品的数量占参赛作品总数32%,对应的是64篇,求单位“1”,用64÷32%解答;
(2)根据比的意义,用教师组参赛作品的数量占参赛作品总数的分率∶小学组参赛作品的数量占参赛作品总数的分率,化简即可解答;
(3)用参赛作品的总数×社会组参赛作品占参赛作品总数的百分率,即可解答。
【详解】(1)64÷32%=200(篇)
本次活动一共有200篇参赛作品。
(2)20%∶40%
=0.2∶0.4
=(0.2÷0.2)∶(0.4÷0.2)
=1∶2
教师组参赛作品的数量与小学组参赛作品的数量的比是1∶2。
(3)200×8%=16(篇)
社会组有16篇参赛作品。
19.(1)200
(2)见详解
(3)见详解
【分析】(1)将调查总人数看作单位“1”,软件诈骗人数÷对应百分率=调查总人数;
(2)调查总人数×虚假中奖对应百分率=虚假中奖人数,总人数-网络诈骗人数-虚假中奖人数-软件诈骗人数=电话欠费人数,据此画出相应直条,标记数据,即可补充条形统计图;
网络诈骗人数÷总人数×100%=网络诈骗对应百分率,电话欠费人数÷总人数×100%=电话欠费对应百分率,据此补充扇形统计图;
(3)答案不唯一,合理即可,如加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电等。
【详解】(1)20÷10%=20÷0.1=200(人)
学校共调查了200人。
(2)200×25%=200×0.25=50(人)
200-90-50-20=40(人)
90÷200×100%
=0.45×100%
=45%
40÷200×100%
=0.2×100%
=20%
(3)为了防止网络诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电,关注国家反诈平台,加强自我道德建设,克服“贪小便宜”、“不劳而获”的思想等。(答案不唯一)
20.(1)600人
(2)见详解
(3)见详解
【分析】(1)将调查的总人数看作单位“1”,刷单返利的人数有60人,占了总人数的10%,根据已知一个数的百分之几是多少,求这个数,用除法,即用刷单返利的人数÷对应百分率=总人数,据此列式计算;
(2)1-刷单返利的对应百分率-虚拟中奖的对应百分率-购物退费的对应百分率=虚拟投资的对应百分率,据此补充扇形统计图;
总人数分别乘虚拟中奖、购物退费和虚拟投资的对应百分率,求出虚拟中奖、购物退费和虚拟投资的人数,补充条形统计图,即根据数据画出长短不同的直条,并注明数量。
(3)例如看到诈骗信息不要轻易相信,直接挂断,或者拒绝接听,不要轻信中奖消息。答案不唯一,合理即可。
【详解】(1)60÷10%=60÷0.1=600(人)
和平社区工作人员一共调查了600人。
(2)1-10%-30%-18%=42%
600×30%=600×0.3=180(人)
600×18%=600×0.18=108(人)
600×42%=600×0.42=252(人)
(3)答案不唯一,如不要轻信陌生来电,拒绝接听诈骗电话,陌生电话接听保持警惕等。
21.①240人
②12,图见解析
③见解析
【分析】①由图可知:参加索玛立方体项目的有24人,占六年级参加数学文化节总人数的10%,用24除以10%就能得到参加“数学文化节”的一共有多少人;
②用第一问求的参加“数学文化节”的总人数乘5%就得到了数学阅读的人数,再用参加数学口算的132人除以参加“数学文化节”的总人数再乘百分之百就能得到参加数学口算人数占六年级参加数学文化节总人数百分之几;
③根据题意,我们可以提一个减法问题:参加汉诺塔的人数比参加数学口算的人数少多少人?
用参加数学口算的人数减去汉诺塔的人数即可解答。(答案不唯一)
【详解】①24÷10%=240(人)
答:参加“数学文化节”的一共有240人。
②240×5%=12(人)
132÷240×100%
=0.55×100%
=55%
如图所示:
项目 数学口算 数学阅读 汉诺塔 索玛立方体 数独
人数 132人 12人 36人 24人 36人
。
③提问:参加汉诺塔的人数比参加数学口算的人数少多少人?
132-36=96(人)
答:参加汉诺塔的人数比参加数学口算的人数少96人。
(答案不唯一)
22.(1)2.16万人;
(2)26.7%
(3)见详解
【分析】(1)根据图示,阅读30分钟以上占了总人数的18%,则用总人数×18%,据此解答既即可。
(2)根据题意,已知2023年人均阅读量11.4本,比2018年增长百分之几?观察图示,2018年的阅读量是9本,我们需要计算增长的阅读量=2023年人均阅读量 2018年人均阅读量。然后计算增长的百分比=(增长的阅读量÷2018年的阅读量)×100%,据此解答即可。
(3)根据题意,可提出问题:不喜欢阅读的少年儿童有多少人?即用:总人数×1%,据此解答即可。
【详解】(1)12×18%=2.16(万)
答:平均每天阅读时间在30分钟及以上的有2.16万人。
(2)11.4-9=2.4(万)
(2.4÷9)×100%
=0.267×100%
≈26.7%
答:比2018年增长26.7%。
(3)不喜欢阅读的少年儿童有多少人?
12×1%=0.12(万)
答:不喜欢阅读的少年儿童有0.12万人。(答案不唯一)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第七单元扇形统计图情境化专练
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.垃圾分类可减少污染,相关部门抽样调查了部分居民小区一段时间内垃圾分类情况,如果想清楚的看出每种生活垃圾占生活垃圾总量的百分比,选用( )比较合适。
A.条形统计图 B.折线统计图 C.扇形统计图 D.无法确定
2.美国人口仅占全球人口的3.5%(约3亿人),但排放的二氧化碳却占全球排放量的24%以上,是世界最大的温室气体排放国。因此,近年来,碳中和的呼声越来越高,各国相应出台了碳中和政策。下列说法错误的是( )。
A.美国每一亿人口碳排放量占全球排放量的8%。
B.美国每一亿人口碳排放量比中国每一亿人口碳排放量多。
C.中国碳排放量是美国的
D.美国与欧盟的碳排放量之和比其他国家排放量之和(不包含中国)都多。
3.地球陆地共分为七个大洲,即亚洲、欧洲、非洲、北美洲、南美洲、大洋洲和南极洲。下图是地球陆地面积分布统计图。根据图中的信息进行判断,关于七个大洲面积之间的关系,以下说法错误的是( )。
在七个大洲中,亚洲面积最大
B.北美洲的面积比南美洲的面积大
和欧洲面积最接近的是大洋洲的面积
D.亚洲与非洲的面积之和大于地球陆地总面积的50%
4.2023年10月8日晚,第19届亚运会在中国杭州圆满闭幕。在本届亚运会上,中国体育代表团再次展现了出色的体育实力。下面是本届亚运会中国体育代表团所获奖牌情况。
金牌 银牌 铜牌
数量/枚 201 111 71
约占本届亚运会中国体育代表团所获奖牌总数的百分比 52.5% 29.0% 18.5%
如果要用统计图清楚地表示金、银、铜牌占本届亚运会中国体育代表团所获奖牌总数的百分比,选择( )比较合适。
A.扇形统计图 B.条形统计图 C.折线统计图 D.复式折线统计图
5.为选拔更出色的运动员参加2024年巴黎奥运会,国家队从近3年就开始为每个队员绘制( ),来表示运动员们参加每次比赛成绩高低的变化。
A.条形统计图 B.折线统计图 C.扇形统计图 D.都不是
二、填空题
6.下图是第29届奥运会中国奖牌情况统计图。
(1)( )项目奖牌数最多,占奖牌总数的( )。( )项目的奖牌数最少,占奖牌总数的( )。
(2)( )和( )项目奖牌数等于( )项目的奖牌数。
(3)第29届奥运会中国奖牌总数为100枚,射击和体操一共获得了( )枚奖牌,占总奖牌数的( )。
7.“直播带货”已成为促进地区经济、文化发展的有效途径。2023年5月20日-5月25日,农产品直播电商平台“东方甄选”在太原古县城举办山西专场。短短6天,全国人民的热切目光对焦山西、上亿元的山西好物销往全国……据统计:此次“东方甄选山西行”销售“山西好物”约达130000000元,此前,仅一条宣传短视频就获得289000的点赞量。130000000读作( ),改写成用“亿”作单位的数是( );289000精确到万位是( )。如果把这6天每天的销售额占总销售额的百分比用统计图表示出来,最适宜选用( )统计图。(填“条形”“扇形”或“折线”)
8.复兴小学一、二年级课后服务开设了阅读、绘画、羽毛球、陶艺四门兴趣课程,要求学生每人选择一门课程参加活动。为了了解学生的选课情况,学校随机抽取了部分学生进行问卷调查,并根据调查结果制成了统计表和统计图。
学生选课情况统计表
课程 选择人数
阅读 20
绘画 a
篮球 b
陶艺 8
学生选课情况统计图
(1)本次问卷调查共抽取( )人;
(2)统计表中a=( ),b=( );
(3)统计图中选篮球的人数占( )%,选陶艺的人数占( )%。
9.为落实国家“双减”政策,学校课后服务数学游戏类活动开设了四个项目:A开心数独,B勇闯华容道,C巧算24点,D起味拼图。为了解学生最喜欢哪种数学游戏,随机抽取了部分学生进行调查(每个学生只能选择其中一项),并将结果绘制成如下两幅不完整的统计图表。
问卷情况统计表
数学游戏项目 人数(人)
A、开心数独 56
B、勇闯华容道 64
C、巧算24点 8
D、趣味拼图
(1)本次一共调查了( )个学生,统计表中( )。
(2)若该校有2000名学生,请你估计该校最喜欢“C巧算24点”的学生约有( )人。
三、作图题
10.春峰小学2024年春季学期开展了“我最喜欢的实践活动场馆”调研,各年级学生参与调研的情况统计如表:
博物馆类 科技馆类 游艺场馆类 其它场馆
一年级 5 15 30 9
二年级 8 15 28 11
三年级 6 32 22 7
四年级 10 41 12 5
五年级 13 40 10 4
六年级 18 45 8 6
合计 60 188 110 42
(1)如图是军军同学对此次调研“最喜欢的实践活动场馆”情况进行整体分析后制作的部分统计图,请你继续完成统计图。
(2)根据统计图表,比较各年级“最喜欢科技类场馆”的情况,在括号写出你对调研结果的看法( )。
四、解答题
11.钱塘小学开展阳光体育运动,调查了六年级男生最喜欢的球类运动项目,并将调查情况制成如下统计表和统计图。
(1)将统计表和统计图中的数据补充完整。
项目 排球 篮球 足球 其他
人数(人) 30 30
(2)已知其他球类项目中,有60%的男生最喜欢乒乓球,最喜欢网球的人数与最喜欢乒乓球的人数的比是1∶3,最喜欢网球的有多少人?
12.我会算。
甲、乙两所学校在艺术节期间共收到各类艺术作品1700件。各类艺术作品的统计情况如下图:
已知甲校收到的剪纸作品比乙校收到的剪纸作品多35件。这两所学校收到的艺术作品的总数分别是多少件?
13.在习总书记“既要金山银山,又要绿水青山”思想的指导下,我国雾霾天气得到了较大改善,某校在学生中做了一次对雾霾知识了解程度的抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解。根据调查结果,绘制了如图所示的不完整的统计图。结合统计图,回答下列问题:
(1)本次参与调查的学生一共有( )人。
(2)“基本了解”的同学占( )。
(3)参与调查的学生中对雾霾情况“非常了解”的人数比“比较了解”的人数少百分之几?
14.对于电动自行车管理问题,《北京市单位消防安全主体责任规定》要求,单位设置的电动自行车停放场所应当符合有关技术标准规定的防火间距、防火分区、充电设施等要求。同时,从严规定了电动自行车禁止入楼的要求,即“制止在建筑物内违规停放电动自行车或者为电动自行车充电的行为”。就这个问题,明明查阅资料了解相关信息如下:
资料一:
今年3月我市共发生电动自行车火灾35起,起火地点均为室外。
(1)请将扇形统计图和条形统计图分别补充完整。
(2)今年3月我市发生电动自行车火灾中,处于停放状态有( )起。
资料二:
电动自行车起火危害极其严重,主要包括:火场高温、有毒烟气的产生、电池爆炸以及救援困难等。
(3)根据明明所查数据和信息,请分析我市“电动自行车禁止入楼”的要求的合理性,写出你的理由。
15.如图是对部分六年级同学进行的“你最喜欢的一种球类运动”问卷调查统计情况,认真读图,完成下列问题。
(1)这是一个( )统计图。
(2)如果最喜欢打排球的有36人,那么这次问卷活动调查了( )人。
(3)根据(2)题的结论,有( )人最喜欢踢足球。
16.山西文旅集团推出五条旅游研学线路(如图):某校为了了解学生对哪条研学线路最感兴趣,从该校六年级学生中随机抽取了若干名学生进行调查,绘制了如图所示的条形统计图和扇形统计图。
请根据以上信息,解答下列问题:
(1)本次参与调查的学生共有多少名?
(2)请将条形统计图补充完整。
(3)在扇形统计图中,E所在的圆心角的度数是( )°。
(4)如果该校六年级共有学生480人,请你估计选择“D游山西,读汇通天下晋商史”的有( )人。
17.王老师对300名五年级学生的课外阅读情况进行调查,绘制了如图统计图。
(1)调查的五年级学生中,从不阅读课外书籍的同学有( )人。
(2)根据题目中的数据,把条形统计图补充完整。
(3)阅读《西游记》的人数大约比阅读《三国演义》的人数多( )。
18.为了弘扬中华优秀传统文化,某市举办了“典籍里的中国”中华经典诵读活动,下图是各个组别参赛作品数量情况统计图。
(1)中学组有64篇参赛作品,本次活动一共有( )篇参赛作品。
(2)教师组参赛作品的数量与小学组参赛作品的数量的比是( )。
(3)社会组有( )篇参赛作品。
19.在“2023年打击电信网络诈骗犯罪行动”中,我国有23个部门和单位联手打击显成效。学校开展“防止电信网络诈骗”的调查活动。同学们将调查结果整理分析后,正在绘制统计图。
(1)学校共调查了( )人。
(2)请将两幅统计图补充完整。
(3)防止网络诈骗,你想对你身边的人说些什么?
20.向阳社区开展防范电信诈骗宣传教育活动,进行了防止“电信网络诈骗”的调查活动,选择“你觉得最容易上当的诈骗方式”,并且每人只能选一项。工作人员将调查结果整理后,绘制了两副不完整的统计图(下图),请根据图中信息按要求作答。
(1)和平社区工作人员一共调查了( )人。
(2)把两个统计图补充完整,其中条形统计图的每个条形上方标注数据。
(3)你有什么防止电信诈骗的秘籍给同学们分享一下?
21.巩义市某小学5月份进行“数学文化节”活动(每人参加一个项目)。六年级学生参加项目信息如下:
项目 数学口算 数学阅读 汉诺塔 索玛立方体 数独
人数 132人 人 36人 24人 36人
①根据统计表和统计图中的信息,请你算出参加“数学文化节”的一共有多少人?
②请把统计表和统计图内信息补充完整。
③请提一个数学问题,并解答。
22.2024年4月23日“世界读书日”发布了《中国少年儿童阅读素养调查研究报告》,参与调查问卷的少年儿童约12万人。以下选取了其中部分统计信息:
(1)平均每天阅读时间在30分钟及以上的有多少万人?
(2)2023年中国少年儿童人均阅读量是11.4本,比2018年增长百分之几?(百分号前保留一位小数)
(3)请你选择相关信息提出一个数学问题,并解决。
参考答案:
1.C
【分析】条形统计图可以清晰反映数据情况,折线统计图可以反映数据的变化情况,扇形统计图可反映部分占整体的百分比情况。据此解题。
【详解】如果想清楚的看出每种生活垃圾占生活垃圾总量的百分比,选用扇形统计图比较合适。
故答案为:C
2.C
【分析】A.将二氧化碳全球排放量看作单位“1”,美国约3亿人,美国二氧化碳排放量对应百分率÷3=美国每一亿人口碳排放量占全球排放量的百分之几;
B.中国约14亿人,中国二氧化碳排放量对应百分率÷14=中国每一亿人口碳排放量占全球排放量的百分之几,与美国每一亿人口碳排放量占全球排放量的百分之几比较即可。
C.将美国碳排放量看作单位“1”,中国碳排放量对应百分率÷美国碳排放量对应百分率=中国碳排放量是美国的几分之几;
D.将美国的碳排放量对应百分率与欧盟的碳排放量对应百分率相加,与其他国家排放量对应百分率比较即可。
【详解】A.24%÷3=8%
美国每一亿人口碳排放量占全球排放量的8%,说法正确;
B.28%÷14=2%
8%>2%,美国每一亿人口碳排放量比中国每一亿人口碳排放量多,说法正确;
C.28%÷24%==
中国碳排放量是美国的,选项说法错误;
D.24%+13%=37%
37%>35%
美国与欧盟的碳排放量之和比其他国家排放量之和(不包含中国)都多,说法正确。
说法错误的是中国碳排放量是美国的。
故答案为:C
3.D
【分析】根据扇形统计图中的信息,比较七个大洲面积之间的大小,逐项分析,进行判断。
【详解】A.29.4>20.2%>16.2%>12%>9.4%>6.8%>6%,在七个大洲中,亚洲面积最大,原题说法正确;
B.16.2%>12%,北美洲的面积比南美洲的面积大,原题说法正确;
C.6.8%与6%最接近,和欧洲面积最接近的是大洋洲的面积,原题说法正确;
D.29.4%+20.2%=49.6%,49.6<50%,亚洲与非洲的面积之和小于地球陆地总面积的50%,原题说法错误。
故答案为:D
4.A
【分析】条形统计图可以清楚地看出数量的多少。
折线统计图不但可以表示出数量的多少,而且能够清楚地表示出数量增减变化的情况。
扇形统计图表示各部分数量与总数之间的关系。
【详解】如果要用统计图清楚地表示金、银、铜牌占本届亚运会中国体育代表团所获奖牌总数的百分比,选择扇形统计图比较合适。
故答案为:A
5.B
【分析】用统计图表示数据时,要根据实际情况选择合适的统计图:(1)要表示出各种数量的多少时,选择条形统计图;(2)既要表示出各种数量的多少,又要表示出数量增减变化的情况时,选择折线统计图;(3)要表示出各部分数量与总数之间的关系时,选择扇形统计图。
【详解】国家队即要了解运动员们3年来参加每次比赛的具体成绩,又要了解成绩的增减变化趋势,所以,国家队从近3年就开始为每个队员绘制折线统计图,来表示运动员们参加每次比赛成绩高低的变化。
故答案为:B
6.(1) 水上 23% 田径 2%
(2) 球类 田径 水上
(3) 29 29%
【分析】(1)比较各项目奖牌数占奖牌总数的百分比即可。
(2)从统计图中找出哪两个项目的奖牌数占奖牌总数的百分比的和等于另一个项目的奖牌数占奖牌总数的百分比即可。
(3)把第29届奥运会中国奖牌总数看作单位“1”,从统计图中可知,射击和体操的奖牌数一共占奖牌总数的(11%+18%),单位“1”已知,用奖牌总数乘(11%+18%),即可求出射击和体操一共获得奖牌的数量。
【详解】(1)23%>22%>21%>18%>11%>3%>2%
(水上)项目奖牌数最多,占奖牌总数的(23%)。(田径)项目的奖牌数最少,占奖牌总数的(2%)。
(2)21%+2%=23%
或18%+3%=21%
(球类)和(田径)项目奖牌数等于(水上)项目的奖牌数。
或(体操)和(其它)项目奖牌数等于(球类)项目的奖牌数。
(3)11%+18%=29%
100×29%
=100×0.29
=29(枚)
第29届奥运会中国奖牌总数为100枚,射击和体操一共获得了(29)枚奖牌,占总奖牌数的(29%)。
7. 一亿三千万 1.3亿 29万 扇形
【分析】整数的读法是从高位到低位,一级一级地读。读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零,据此读出此数;
改写成用“亿”作单位的数,就在亿位的右下角点上小数点,同时小数末尾的0去掉,并在后面加个“亿”字;精确到万位,则看千位上的数,如果千位上的数大于等于5,则进一,小于5,则舍去,后面加个“万”字;
根据统计图的特点:折线统计图可以清楚的观察数量的增减变化情况;条形统计图可以清晰的看出数量的多少;扇形统计图可以反应部分与整体之间的关系,据此即可选择。
【详解】由分析可知:
130000000读作:一亿三千万,改写成用“亿”作单位的数是1.3亿,289000精确到万位是29万。如果把这6天每天的销售额占总销售额的百分比用统计图表示出来,最适宜选用扇形统计图。
8.(1)80
(2) 24 28
(3) 35 10
【分析】(1)用选阅读的人数除以阅读人数占的百分率,即可求出一共抽取的人数;
(2)用一共抽取的人数乘绘画人数占的百分率,即可求出选绘画的人数,再用抽取的总人数减去选阅读、绘画、陶艺的人数即可求出选篮球的人数;
(3)用选篮球的人数除以抽取的总人数,求出选篮球的人数占的百分率;同理用选陶艺的人数除以抽取的总人数,求出选陶艺的人数占的百分率。
【详解】(1)抽取人数:(人)
(2)a
b
(3)选篮球的人数占总人数的:
选陶艺的人数占总人数的:
【点睛】本题查扇形统计图的应用,能够根据统计图表提供的信息,解决有关的实际问题,是解题的关键。
9.(1) 160 32
(2)100
【分析】(1)观察统计图表,根据项有56人,项占总人数的,用A项的人数除以A项占总人数的百分率,求出调查的总人数;再用总人数减去A、B和C三项人数,即可得出趣味拼图人数;
(2)用调查的统计图表的数据计算估计:调查的人数中,开心数独项目有56人,巧算24点有8人,占开心数独的,即相当于总数的的;也就是总数的,据此可估算出喜欢巧算24点的学生约有多少人。
【详解】(1)(人)
(人)
本次一共调查了160个学生,统计表中的等于32。
(2)
(人)
按调查数据推算,若该校有2000名学生,该校最喜欢“巧算24点”的学生约有100人。
10.(1)见详解
(2)见详解
【分析】(1)根据调研情况统计表分别计算出博物馆类、科技馆类、游艺场馆类、其他场馆占全部调研情况的占比后绘制扇形统计图即可;
(2)分别计算出每个年级“最喜欢科技类场馆”的占比情况后发表看法(答案不唯一,合理即可)。
【详解】(1)60+188+110+42=400(人)
博物馆类:60÷400=15%
科技馆类:188÷400=47%
游艺场馆类:110÷400=27.5%
其它场馆:42÷400=10.5%
47%>27.5%>15%>10.5%
完成的统计图,如图:
(2)一年级科技馆类:
15÷(5+15+30+9)
=15÷59
≈25.4%
二年级科技馆类:
15÷(8+15+28+11)
=15÷62
≈24.2%
三年级科技馆类:
32÷(6+32+22+7)
=32÷67
≈47.8%
四年级科技馆类:
41÷(10+41+12+5)
=41÷68
≈60.3%
五年级科技馆类:
40÷(13+40+10+4)
=40÷67
≈59.7%
六年级科技馆类:
45÷(18+45+8+6)
=45÷77
≈58.4%
60.3%>59.7%>58.4%>47.8%>25.4%>24.2%
因此可得,四年级“最喜欢科技类场馆”的占比最高。(答案不唯一)
11.(1)见详解;
(2)3人
【分析】(1)将男生总人数看作单位“1”,观察扇形统计图可知,喜欢排球的人数是总人数的25%,1-喜欢篮球的对应百分率-喜欢排球的对应百分率-喜欢其他的对应百分率=喜欢足球的对应百分率;喜欢排球的人数÷对应百分率=总人数,总人数×喜欢足球的对应百分率=喜欢足球的人数,总人数×喜欢其他的对应百分率=喜欢其他的人数,据此求出相关数据,补充统计表和统计图即可;
(2)将喜欢其他球类的人数看作单位“1”,喜欢其他球类的人数×最喜欢乒乓球的人数对应百分率=最喜欢乒乓球的人数,将比的前后项看成份数,最喜欢乒乓球的人数÷对应份数=一份数,一份数×最喜欢网球的对应份数=最喜欢网球的人数。
【详解】(1)1-25%-25%-12.5%=37.5%
30÷25%=30÷0.25=120(人)
120×37.5%=120×0.375=45(人)
120×12.5%=120×0.125=15(人)
项目 排球 篮球 足球 其他
人数(人) 30 30 45 15
(2)15×60%
=15×0.6
=9(人)
9÷3×1=3(人)
答:最喜欢网球的有3人。
12.800件;900件
【分析】观察统计 图可知,甲校剪纸作品占10%,乙校剪纸作品占5%。又知甲、乙两所学校共收到各类艺术作品1700件,甲校收到的剪纸作品比乙校收到的剪纸作品多35件。可列方程解答,设甲校收到x件艺术作品,则乙校收到(1700-x)件艺术作品。甲校的剪纸作品有10%x件,乙校的剪纸作品有(1700-x)×5%件,所以10%x-(1700-x)×5%=35,解此方程求出甲校收到的艺术作品件数,进而求出乙校收到的艺术作品件数。
【详解】解:设甲校收到艺术作品的总数是x件。
10%x-(1700-x)×5%=35
10%x-85+5%x=35
15%x-85=35
15%x-85+85=35+85
15%x=120
15%x÷15%=120÷15%
x=800
乙校:1700-800=900(件)
答:甲校收到艺术作品800件,乙校收到艺术作品900件。
13.(1)400
(2)40
(3)75%
【分析】(1)把调查的学生总人数看作单位“1”,根据条形统计图和扇形统计图可知,“非常了解”的人数占调查的学生总人数的5%,对应的是20人,求单位“1”,用20÷5%解答;
(2)“基本了解”的人数÷调查的学生总人数×100%,即可求出“基本了解”的同学占调查学生人数的百分比;
(3)把“比较了解”的人数看作单位“1”,用非常了解”的人数与“比较了解”的人数差,除以“比较了解”的人数,再乘100%,即可解答。
【详解】(1)20÷5%=400(人)
本次参与调查的学生一共有400人。
(2)160÷400×100%
=0.4×100%
=40%
“基本了解”的同学占40%。
(3)(80-20)÷80×100%
=60÷80×100%
=0.75×100%
=75%
答:参与调查的学生中对雾霾情况“非常了解”的人数比“比较了解”的人数少75%。
14.(1)见详解
(2)26
(3)见详解
【分析】(1)电动车起火时状态为行驶状态和停放状态,根据扇形统计图可知,停放状态时起火占比为74.3%,则行驶状态时起火占比为1-74.3%=25.7%;根据北京市3月份起火数量35起可知,电池故障原因起火23起,其他原因起火4起,则线路故障起火为35-23-4=8起,据此完成统计图的绘制;
(2)求一个数的百分之几是多少,用乘法计算,用起火数量乘停放状态起火占起火数量的百分
数即可求解;
(3)根据统计的结果,说明电动车进楼的危害即可。
【详解】(1)1-74.3%=25.7%
35-23-4
=12-4
=8(起)
如图所示:
(2)35×74.3%≈26(起)
则今年3月我市发生电动自行车火灾中,处于停放状态有26起。
(3)电动自行车进楼容易引发火灾,造成重大事故;堵塞楼道,埋下安全隐患;加速电梯损坏,带来运行风险。
15.(1)扇形
(2)200
(3)48
【分析】(1)扇形统计图:用整圆表示总数,各扇形表示部分占总数的百分比,能直观体现部分与总数的关系,扇形大小反映占比大小。
(2)已知最喜欢打排球的人数占比为18%,人数为36人。用最喜欢打排球的人数除以其占总人数的百分比,即可得到总人数。
(3)已知总人数和最喜欢踢足球的人数占比为24%。用总人数乘最喜欢踢足球的人数占比,就能得出最喜欢踢足球的人数。
【详解】(1)综上分析所述,这是一个扇形统计图。
(2)因为最喜欢打排球的人数占总人数的18%,且最喜欢打排球的有36人,所以总人数为:36÷18%=36÷0.18=200(人)
那么这次问卷活动调查了200人。
(3)因为最喜欢踢足球的人数占总人数的24%,总人数为200人,所以最喜欢踢足球的人数为:200×24%=200×0.24=48(人)
有48人最喜欢踢足球。
16.(1)80名
(2)见详解
(3)90
(4)102
【分析】(1)由题意可知,对A路线感兴趣的学生有16人,占总人数的20%,根据已知一个数的百分之几是多少,求这个数,用除法计算,即用16除以20%即可;
(2)用总人数分别减去对A、B、C、E路线感兴趣的人数即可求出对D感兴趣的人数,进而完成条形统计图即可;
(3)用选择用E的人数除以总人数,化为分数形式,再根据分数的基本性质化为分母为360的分数即可;
(4)先求出选择D游山西的人数占总人数的分率,再根据求一个数的几分之几是多少,用乘法计算即可。
【详解】(1)16÷20%=80(名)
答:本次参与调查的学生共有80名。
(2)80-16-13-14-20
=64-13-14-20
=51-14-20
=37-20
=17(名)
如图所示:
(3)20÷80=
在扇形统计图中,E所在的圆心角的度数是90°。
(4)17÷80=
480×=102(人)
则选择“D游山西,读汇通天下晋商史”的有102人。
17.(1)30
(2)见详解
(3)23.1
【分析】(1)由题意可知,被调查的300名五年级学生中有10%的学生从不阅读,根据求一个数的百分之几是多少,用乘法解答,用300乘10%即可解答。
(2)把被调查的300名五年级学生看作单位“1”,用“1”减去偶尔阅读、从不阅读的学生占单位“1”的百分率的和,求出经常阅读的学生占总数的百分率,再根据求一个数的百分之几是多少,用乘法解答求出经常阅读的人数,再用经常阅读的人数减去阅读其它三种图书的人数和,求出阅读《水浒传》的人数,据此数据完成条形统计图。
(3)根据求一个数比另一个数多百分之几,用两个数的差除以另一个数解答即可。
【详解】(1)300×10%=30(人)
所以从不阅读的同学有30人。
(2)1-(10%+20%)
=1-30%
=70%
300×70%-(80+18+65)
=210-(98+65)
=210-163
=47(人)
如下图:
(3)(80-65)÷65
=15÷65
≈23.1%
答:阅读《西游记》的人数大约比阅读《三国演义》的人数多23.1%。
18.(1)200
(2)1∶2
(3)16
【分析】(1)把参赛作品的总数看作单位“1”,中学组参赛作品的数量占参赛作品总数32%,对应的是64篇,求单位“1”,用64÷32%解答;
(2)根据比的意义,用教师组参赛作品的数量占参赛作品总数的分率∶小学组参赛作品的数量占参赛作品总数的分率,化简即可解答;
(3)用参赛作品的总数×社会组参赛作品占参赛作品总数的百分率,即可解答。
【详解】(1)64÷32%=200(篇)
本次活动一共有200篇参赛作品。
(2)20%∶40%
=0.2∶0.4
=(0.2÷0.2)∶(0.4÷0.2)
=1∶2
教师组参赛作品的数量与小学组参赛作品的数量的比是1∶2。
(3)200×8%=16(篇)
社会组有16篇参赛作品。
19.(1)200
(2)见详解
(3)见详解
【分析】(1)将调查总人数看作单位“1”,软件诈骗人数÷对应百分率=调查总人数;
(2)调查总人数×虚假中奖对应百分率=虚假中奖人数,总人数-网络诈骗人数-虚假中奖人数-软件诈骗人数=电话欠费人数,据此画出相应直条,标记数据,即可补充条形统计图;
网络诈骗人数÷总人数×100%=网络诈骗对应百分率,电话欠费人数÷总人数×100%=电话欠费对应百分率,据此补充扇形统计图;
(3)答案不唯一,合理即可,如加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电等。
【详解】(1)20÷10%=20÷0.1=200(人)
学校共调查了200人。
(2)200×25%=200×0.25=50(人)
200-90-50-20=40(人)
90÷200×100%
=0.45×100%
=45%
40÷200×100%
=0.2×100%
=20%
(3)为了防止网络诈骗,我想对身边的人说:加强自我防范意识,保护好个人信息,不点击未知链接,不轻信陌生来电,关注国家反诈平台,加强自我道德建设,克服“贪小便宜”、“不劳而获”的思想等。(答案不唯一)
20.(1)600人
(2)见详解
(3)见详解
【分析】(1)将调查的总人数看作单位“1”,刷单返利的人数有60人,占了总人数的10%,根据已知一个数的百分之几是多少,求这个数,用除法,即用刷单返利的人数÷对应百分率=总人数,据此列式计算;
(2)1-刷单返利的对应百分率-虚拟中奖的对应百分率-购物退费的对应百分率=虚拟投资的对应百分率,据此补充扇形统计图;
总人数分别乘虚拟中奖、购物退费和虚拟投资的对应百分率,求出虚拟中奖、购物退费和虚拟投资的人数,补充条形统计图,即根据数据画出长短不同的直条,并注明数量。
(3)例如看到诈骗信息不要轻易相信,直接挂断,或者拒绝接听,不要轻信中奖消息。答案不唯一,合理即可。
【详解】(1)60÷10%=60÷0.1=600(人)
和平社区工作人员一共调查了600人。
(2)1-10%-30%-18%=42%
600×30%=600×0.3=180(人)
600×18%=600×0.18=108(人)
600×42%=600×0.42=252(人)
(3)答案不唯一,如不要轻信陌生来电,拒绝接听诈骗电话,陌生电话接听保持警惕等。
21.①240人
②12,图见解析
③见解析
【分析】①由图可知:参加索玛立方体项目的有24人,占六年级参加数学文化节总人数的10%,用24除以10%就能得到参加“数学文化节”的一共有多少人;
②用第一问求的参加“数学文化节”的总人数乘5%就得到了数学阅读的人数,再用参加数学口算的132人除以参加“数学文化节”的总人数再乘百分之百就能得到参加数学口算人数占六年级参加数学文化节总人数百分之几;
③根据题意,我们可以提一个减法问题:参加汉诺塔的人数比参加数学口算的人数少多少人?
用参加数学口算的人数减去汉诺塔的人数即可解答。(答案不唯一)
【详解】①24÷10%=240(人)
答:参加“数学文化节”的一共有240人。
②240×5%=12(人)
132÷240×100%
=0.55×100%
=55%
如图所示:
项目 数学口算 数学阅读 汉诺塔 索玛立方体 数独
人数 132人 12人 36人 24人 36人
。
③提问:参加汉诺塔的人数比参加数学口算的人数少多少人?
132-36=96(人)
答:参加汉诺塔的人数比参加数学口算的人数少96人。
(答案不唯一)
22.(1)2.16万人;
(2)26.7%
(3)见详解
【分析】(1)根据图示,阅读30分钟以上占了总人数的18%,则用总人数×18%,据此解答既即可。
(2)根据题意,已知2023年人均阅读量11.4本,比2018年增长百分之几?观察图示,2018年的阅读量是9本,我们需要计算增长的阅读量=2023年人均阅读量 2018年人均阅读量。然后计算增长的百分比=(增长的阅读量÷2018年的阅读量)×100%,据此解答即可。
(3)根据题意,可提出问题:不喜欢阅读的少年儿童有多少人?即用:总人数×1%,据此解答即可。
【详解】(1)12×18%=2.16(万)
答:平均每天阅读时间在30分钟及以上的有2.16万人。
(2)11.4-9=2.4(万)
(2.4÷9)×100%
=0.267×100%
≈26.7%
答:比2018年增长26.7%。
(3)不喜欢阅读的少年儿童有多少人?
12×1%=0.12(万)
答:不喜欢阅读的少年儿童有0.12万人。(答案不唯一)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
