天长市炳辉中学沪教版七年级数学下册8.3完全平方公式与平方差公式课件(共25张PPT)
文档属性
| 名称 | 天长市炳辉中学沪教版七年级数学下册8.3完全平方公式与平方差公式课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 123.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-06 14:48:42 | ||
图片预览




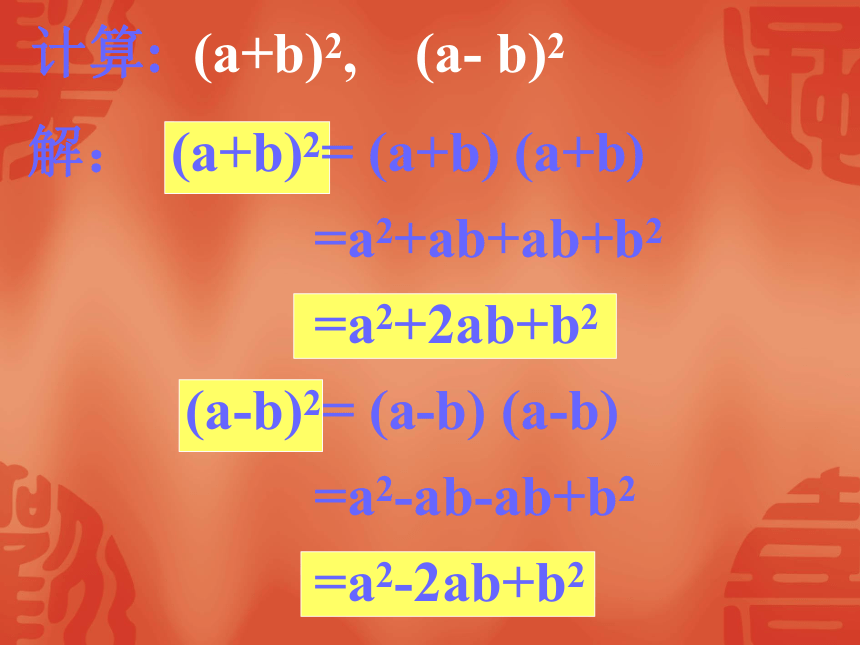

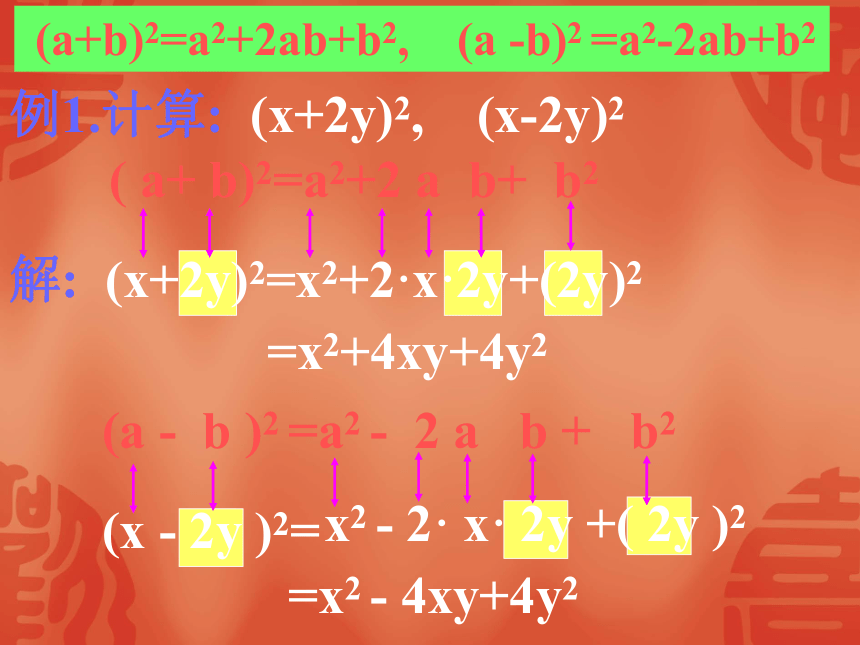

文档简介
课件25张PPT。完全平方公式乘法公式:(x+a)(x+b)=x2+(a+b)x+ab(a+b)(a-b)=a2-b2——平方差公式1.当a=-b时1.下列计算正确的是( )
A. (x-6)(x+6)=x2-6
B. (3x-1)(3x+1)=3x2-1
C. (-1+x)(-1-x)=x2-1
D. (5ab+1)(5ab-1)=25a2b2-1
2.填空:
1) ( )( ) = m2-n2
2) (2m-1)( ) = 4m2-1
3) (-2m+1)( ) = 1-4m2
3.计算: (a+2b+3)(a+2b-3)D2m+1m-nm+n2m+13.计算: (a+2b+3)(a+2b-3)解:原式= [ (a+2b)+3][(a+2b)-3]
= (a+2b)2-32
= (a+2b)(a+2b)-9
= a2+2ab+2ab+4b2-9
= a2+4ab+4b2-9计算: (a+b)2, (a- b)2解: (a+b)2= (a+b) (a+b)
=a2+ab+ab+b2
=a2+2ab+b2
(a-b)2= (a-b) (a-b)
=a2-ab-ab+b2
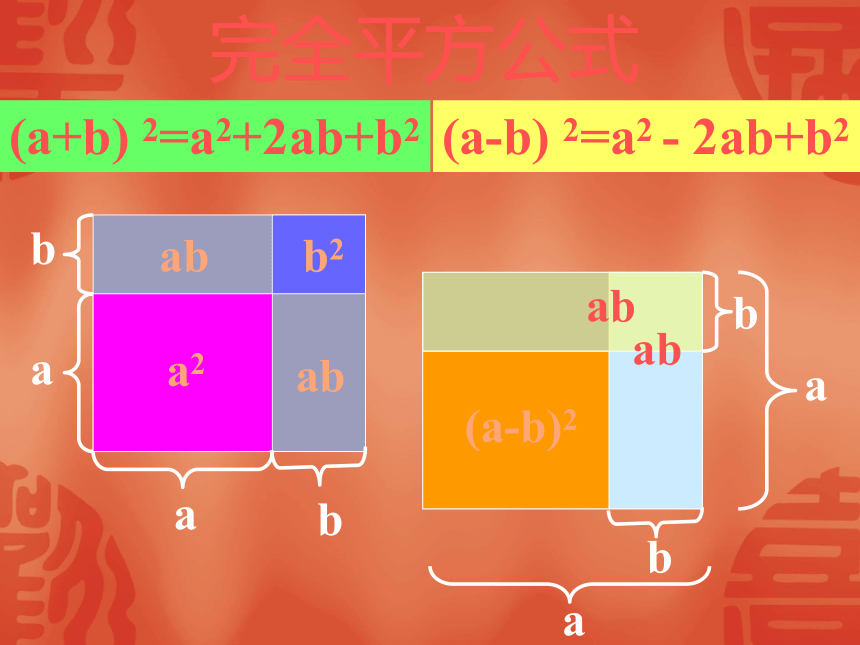
=a2-2ab+b2完全平方公式(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2 两数和(或差)的平方,等于它们
的平方和,加上(或者减去)它们的积
的2倍.完全平方公式(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2bbaaababa2b2baba(a-b)2abab (a+b)2=a2+2ab+b2, (a -b)2 =a2-2ab+b2例1.计算: (x+2y)2, (x-2y)2解: (x+2y)2=( a+ b)2=a2+2 a b+ b2=x2+4xy+4y2(x - 2y )2=(a - b )2 =a2 - 2 a b + b2x2 - 2· x· 2y +( 2y )2 x2+2·x·2y+(2y)2=x2 - 4xy+4y2解:1) (4a-b)2 = (4a)2-2·4a·b+b2
= 16a2-8ab+b2 3) (-2x-1)2 =[-(2x+1)]2=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1练习:P130-1例3.运用完全平方公式计算:
1) 1022 2) 1992
3) 4982 4) 79.82解:1) 1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
2)1992 = (200-1)2 =2002-2×200×1+12
= 40000-400+1
= 39601例3.运用完全平方公式计算:
1) 1022 2) 1992
3) 4982 4) 79.82解:3) 4982 = (500-2)2
= 5002-2×500×2+22
= 250000-2000+4 = 248004
4)79.82 = (80-0.2)2
=802-2×80×0.2+0.22
= 6400-32+0.04
= 6368.04练习:P130-3练习:
指出下列各式中的错误,并加以改正:
1) (-a-1)2 = -a2-2a-1;
2) (2a+1)2 =4a2+1;
3) (2a-1)2 =2a2 – 2a+1.解:1) (-a-1)2
= [-(a+1)]2
= (a+1)2
= a2+2a+1练习:
指出下列各式中的错误,并加以改正:
1) (-a-1)2 = -a2-2a-1;
2) (2a+1)2 =4a2+1;
3) (2a-1)2 =2a2 – 2a+1.解:2) (2a+1)2
= (2a)2+2·(2a) ·1+12
=4a2+4a+1练习:
指出下列各式中的错误,并加以改正:
1) (-a-1)2 = -a2-2a-1;
2) (2a+1)2 =4a2+1;
3) (2a-1)2 =2a2 – 2a+1.解:3) (2a-1)2
= (2a)2-2·(2a) ·1+12
=4a2- 4a+1乘法公式:(x+a)(x+b)=x2+(a+b)x+ab(a+b)(a-b)=a2-b2——平方差公式1.当a=-b时2.当a=b时(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2——完全平方公式小结:
1.完全平方公式是多项式乘法的特殊
情况,要熟记公式的左边和右边的
特点;
2.有时式子需要先进行变形,使变形
后的式子符合应用完全平方公式的
条件,即为“两数和(或差)”的平方,
然后应用公式计算.想一想:(a+b)2与(-a-b)2相等吗?
(a-b)2 与(b-a)2相等吗?为什么?完全平方公式完全平方公式(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2 两数和(或差)的平方,等于它们
的平方和,加上(或者减去)它们的积
的2倍.1.(口答)运用完全平方公式计算:
1) (a+2b)2 2) (-a-2b)2
3) (m-4n)2 4) (4n-m)2
5) ( x+5)2 6) (m- ab)22. 怎样计算(a+b+c)2 ?解:(a+b+c)2 =[(a+b)+c]2
=(a+b)2+2·(a+b) ·c+c2
=a2+2ab+c2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc(a+b+c)2=a2+b2+c2+2ab+2ac+2bc3. 运用乘法公式计算(-a+b-c)2 解法一:用二项完全平方公式计算
(-a+b-c)2= [(-a+b)-c]2
= (-a+b)2-2·(-a+b) ·c+c2
= a2-2ab+b2+2ac-2bc+c2
= a2+b2+c2-2ab+2ac-2bc解法二:用三项完全平方公式计算
(-a+b-c)2
= (-a)2+b2+(-c)2+2(-a)b+2(-a)(-c)+2b(-c)
= a2+b2+c2-2ab+2ac-2bc6.填空:
1) a2+ +b2=(a+b)2
2) a2+ +b2=(a - b)2
3) 4a2+ +b2=(2a+b)2
4) 4a2+ +b2=(2a - b)2
5) ( )2+4ab+b2=( +b)2
6) a2-8ab+ =( )22ab(-2ab)4ab(-4ab)2a2a16b2a-4b练习:p132-2小结:
1.平方差公式:(a+b)(a-b)=a2-b2
完全平方公式:(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
2.公式中的字母,既可表示一个数,也可表示
一个代数式.因此对于较复杂的代数式,常用
化繁为简(换元)的方法,转化成符合公式
形式的式子后应用公式计算;
3.在混合运算中,要注意运算顺序和符号;并
观察哪些式子可直接用公式计算?哪些式子
变形后可用公式计算?哪些式子只能用多项
式乘法法则计算?思考:
1.运用乘法公式计算:
1) (2a-b-c)2
2) (1-x)(1+x)(1+x2)+(1-x2)2
3) (x+2y+3z)2-(x-2y+3z)2
2.已知 .求:
(1) (2)
A. (x-6)(x+6)=x2-6
B. (3x-1)(3x+1)=3x2-1
C. (-1+x)(-1-x)=x2-1
D. (5ab+1)(5ab-1)=25a2b2-1
2.填空:
1) ( )( ) = m2-n2
2) (2m-1)( ) = 4m2-1
3) (-2m+1)( ) = 1-4m2
3.计算: (a+2b+3)(a+2b-3)D2m+1m-nm+n2m+13.计算: (a+2b+3)(a+2b-3)解:原式= [ (a+2b)+3][(a+2b)-3]
= (a+2b)2-32
= (a+2b)(a+2b)-9
= a2+2ab+2ab+4b2-9
= a2+4ab+4b2-9计算: (a+b)2, (a- b)2解: (a+b)2= (a+b) (a+b)
=a2+ab+ab+b2
=a2+2ab+b2
(a-b)2= (a-b) (a-b)
=a2-ab-ab+b2
=a2-2ab+b2完全平方公式(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2 两数和(或差)的平方,等于它们
的平方和,加上(或者减去)它们的积
的2倍.完全平方公式(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2bbaaababa2b2baba(a-b)2abab (a+b)2=a2+2ab+b2, (a -b)2 =a2-2ab+b2例1.计算: (x+2y)2, (x-2y)2解: (x+2y)2=( a+ b)2=a2+2 a b+ b2=x2+4xy+4y2(x - 2y )2=(a - b )2 =a2 - 2 a b + b2x2 - 2· x· 2y +( 2y )2 x2+2·x·2y+(2y)2=x2 - 4xy+4y2解:1) (4a-b)2 = (4a)2-2·4a·b+b2
= 16a2-8ab+b2 3) (-2x-1)2 =[-(2x+1)]2=(2x+1)2
= (2x)2+2·2x·1+1
=4x2+4x+1练习:P130-1例3.运用完全平方公式计算:
1) 1022 2) 1992
3) 4982 4) 79.82解:1) 1022 = (100+2)2
= 1002+2×100×2+22
= 10000+400+4
= 10404
2)1992 = (200-1)2 =2002-2×200×1+12
= 40000-400+1
= 39601例3.运用完全平方公式计算:
1) 1022 2) 1992
3) 4982 4) 79.82解:3) 4982 = (500-2)2
= 5002-2×500×2+22
= 250000-2000+4 = 248004
4)79.82 = (80-0.2)2
=802-2×80×0.2+0.22
= 6400-32+0.04
= 6368.04练习:P130-3练习:
指出下列各式中的错误,并加以改正:
1) (-a-1)2 = -a2-2a-1;
2) (2a+1)2 =4a2+1;
3) (2a-1)2 =2a2 – 2a+1.解:1) (-a-1)2
= [-(a+1)]2
= (a+1)2
= a2+2a+1练习:
指出下列各式中的错误,并加以改正:
1) (-a-1)2 = -a2-2a-1;
2) (2a+1)2 =4a2+1;
3) (2a-1)2 =2a2 – 2a+1.解:2) (2a+1)2
= (2a)2+2·(2a) ·1+12
=4a2+4a+1练习:
指出下列各式中的错误,并加以改正:
1) (-a-1)2 = -a2-2a-1;
2) (2a+1)2 =4a2+1;
3) (2a-1)2 =2a2 – 2a+1.解:3) (2a-1)2
= (2a)2-2·(2a) ·1+12
=4a2- 4a+1乘法公式:(x+a)(x+b)=x2+(a+b)x+ab(a+b)(a-b)=a2-b2——平方差公式1.当a=-b时2.当a=b时(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2——完全平方公式小结:
1.完全平方公式是多项式乘法的特殊
情况,要熟记公式的左边和右边的
特点;
2.有时式子需要先进行变形,使变形
后的式子符合应用完全平方公式的
条件,即为“两数和(或差)”的平方,
然后应用公式计算.想一想:(a+b)2与(-a-b)2相等吗?
(a-b)2 与(b-a)2相等吗?为什么?完全平方公式完全平方公式(a+b) 2=a2+2ab+b2(a-b) 2=a2 - 2ab+b2 两数和(或差)的平方,等于它们
的平方和,加上(或者减去)它们的积
的2倍.1.(口答)运用完全平方公式计算:
1) (a+2b)2 2) (-a-2b)2
3) (m-4n)2 4) (4n-m)2
5) ( x+5)2 6) (m- ab)22. 怎样计算(a+b+c)2 ?解:(a+b+c)2 =[(a+b)+c]2
=(a+b)2+2·(a+b) ·c+c2
=a2+2ab+c2+2ac+2bc+c2
=a2+b2+c2+2ab+2ac+2bc(a+b+c)2=a2+b2+c2+2ab+2ac+2bc3. 运用乘法公式计算(-a+b-c)2 解法一:用二项完全平方公式计算
(-a+b-c)2= [(-a+b)-c]2
= (-a+b)2-2·(-a+b) ·c+c2
= a2-2ab+b2+2ac-2bc+c2
= a2+b2+c2-2ab+2ac-2bc解法二:用三项完全平方公式计算
(-a+b-c)2
= (-a)2+b2+(-c)2+2(-a)b+2(-a)(-c)+2b(-c)
= a2+b2+c2-2ab+2ac-2bc6.填空:
1) a2+ +b2=(a+b)2
2) a2+ +b2=(a - b)2
3) 4a2+ +b2=(2a+b)2
4) 4a2+ +b2=(2a - b)2
5) ( )2+4ab+b2=( +b)2
6) a2-8ab+ =( )22ab(-2ab)4ab(-4ab)2a2a16b2a-4b练习:p132-2小结:
1.平方差公式:(a+b)(a-b)=a2-b2
完全平方公式:(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
2.公式中的字母,既可表示一个数,也可表示
一个代数式.因此对于较复杂的代数式,常用
化繁为简(换元)的方法,转化成符合公式
形式的式子后应用公式计算;
3.在混合运算中,要注意运算顺序和符号;并
观察哪些式子可直接用公式计算?哪些式子
变形后可用公式计算?哪些式子只能用多项
式乘法法则计算?思考:
1.运用乘法公式计算:
1) (2a-b-c)2
2) (1-x)(1+x)(1+x2)+(1-x2)2
3) (x+2y+3z)2-(x-2y+3z)2
2.已知 .求:
(1) (2)
