2024-2025学年北师大版八年级数学上册第一阶段《第1—3章》综合练习题(含详解)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学上册第一阶段《第1—3章》综合练习题(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 233.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 16:10:53 | ||
图片预览




文档简介
2024-2025学年北师大版八年级数学上册第一阶段《第1—3章》综合练习题(附答案)
一、单项选择题(共30分)
1.下列实数中是无理数的是( )
A. B.π C.0.38 D.
2.如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是( )
A.12 B.13 C.144 D.194
3.冰墩墩是2022年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,深受各国人们的欢迎.在图中,将冰墩墩放入坐标系中,它盖住的点的坐标可能为( )
A.(﹣1,﹣2) B.(﹣1,2) C.(1,2) D.(1,﹣2)
4.下列计算正确的是( )
A. B. C. D.
5.点P在第四象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标( )
A.(3,﹣4) B.(﹣4,3) C.(﹣3,4) D.(4,﹣3)
6.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为( )
A.2 B.﹣1 C. D.
7.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A.直角三角形两个锐角互余 B.三角形的稳定性
C.勾股定理 D.勾股定理的逆定理
8.葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其常绕着附近的树干沿最短路线盘旋而上.现有一段葛藤绕树干盘旋2圈升高为2.4m,如果把树干看成圆柱体,其底面周长是0.5m,如图是葛藤盘旋1圈的示意图,则这段葛藤的长是( )m.
A.1.3 B.2.5 C.2.6 D.2.8
9.,,则1720的平方根为( )
A.13.11 B.±13.11 C.41.47 D.±41.47
10.如图,我们把1,1,2,3,5,8,13,21,…这一列数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°的圆弧P1P2、P2P3、P3P4…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,得到螺旋折线,已知点P1(0,1)、P2(﹣1,0)、P3(0,﹣1),则该折线上的点P7的坐标为( )
A.(1,﹣9) B.(﹣1,8) C.(2,﹣8) D.(2,﹣9)
二、填空题(本题共24分)
11.﹣27的立方根是 ;0.16的平方根是 ;﹣的倒数是 .
12.点M(m+1,3﹣2m)在y轴上,则点M坐标为 .
13.山西督军府旧址是晋文公重耳庙,历代山西巡抚的衙门设在此.1916年,各省军务长官改称为督军,阎锡山任督军,因此称督军府.督军府主要由门楼、前院、渊谊堂、小自省堂、梅山等组成.如图所示,门楼的坐标是(0,0),渊谊堂的坐标是(0,2),则梅山的坐标是 .
14.一个三角形三条边的长分别是9cm,12cm,15cm,这个三角形最长边上的高为 .
15.某工厂去年的总产值比总支出多500万元,而今年计划的总产值比总支出多950万元,已知今年计划总产值比去年增加15%,而计划总支出比去年减少10%,求去年计划的总产值和总支出各是多少万元?解:设去年计划的总产值、总支出分别是x万元、y万元,根据题意,可列方程组 .
16.在平面直角坐标系中,对于点A(x,y),若点B的坐标为(x+ay,ax+y),则称点B是点A的a级亲密点.例如:点A(﹣2,6)的级亲密点为B(﹣2+×6,×(﹣2)+6),即点B的坐标为(1,5).
A题:已知点C(﹣1,5)的3级亲密点是点D,则点D的坐标为 .
B题:若点E在x轴上,点E不与原点重合,点E的a级亲密点为点F,且EF的长度为OE长度的倍,则a的值= .
三、解答题(共66分)
17.计算:
(1)2+3﹣3.
(2)(﹣)×(﹣)++(3.14﹣π)0.
(3)x2﹣121=0;
(4)2(x+1)3+16=0.
18.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
19.某市创建文明城市,采用移动宣讲的形式进行宣传动员,如图,笔直公路MN的一侧点A处有一学校,学校A到公路MN的距离AB=480米,若宣讲车P周围800米以内能听到广播宣传,宣讲车P在公路MN上延M到N的方向行驶时.
(1)请问学校A能否听到宣传,请说明理由.
(2)如果能听到,已知宣讲车的速度是256米/分,求学校A总共能听到多长时间的宣传.
20.如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;
(2)若将点A、B、C的纵坐标不变,横坐标分别乘﹣1,得到△A'B'C',在图中画出△A'B'C',此时△A'B'C'与△ABC的位置关系是 ;
(3)已知P为y轴上一点,若△ABP的面积为4,则点P的坐标是 .
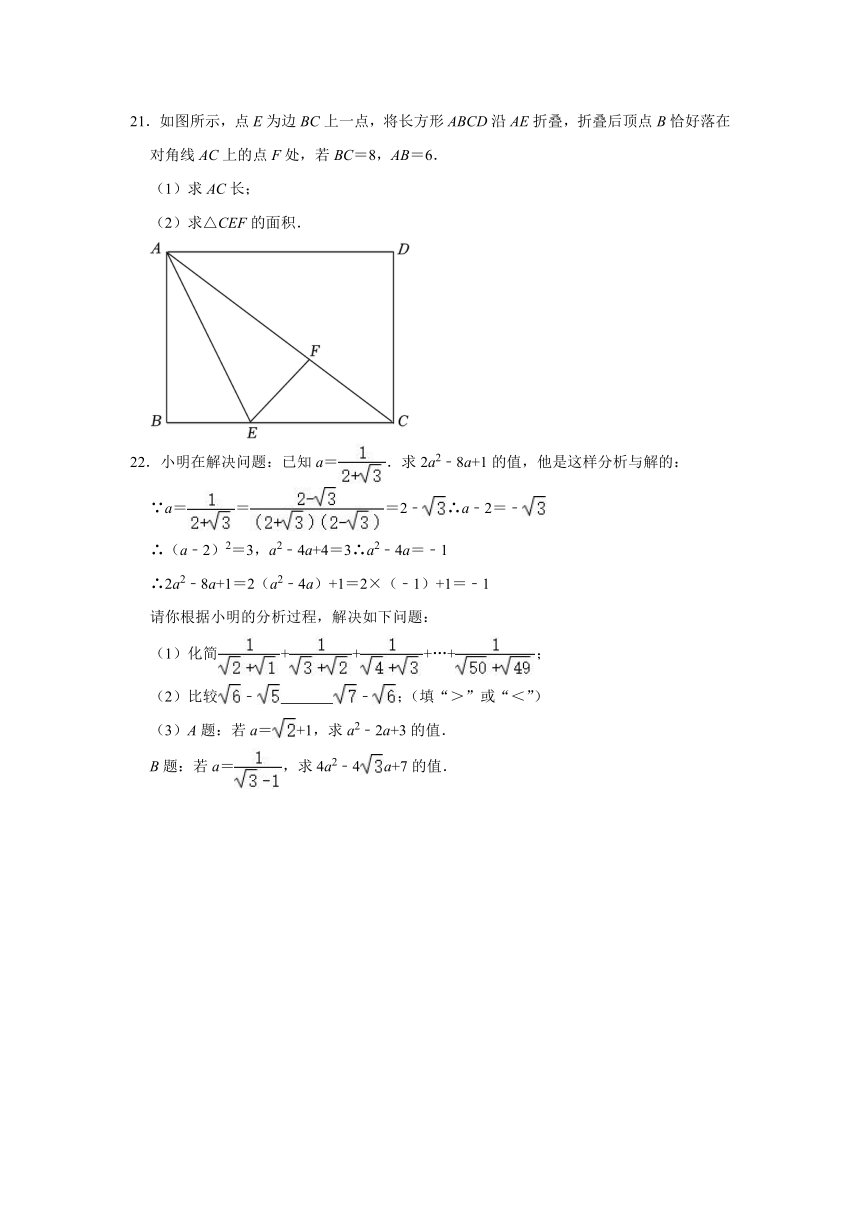
21.如图所示,点E为边BC上一点,将长方形ABCD沿AE折叠,折叠后顶点B恰好落在对角线AC上的点F处,若BC=8,AB=6.
(1)求AC长;
(2)求△CEF的面积.
22.小明在解决问题:已知a=.求2a2﹣8a+1的值,他是这样分析与解的:
∵a===2﹣∴a﹣2=﹣
∴(a﹣2)2=3,a2﹣4a+4=3∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1
请你根据小明的分析过程,解决如下问题:
(1)化简+++…+;
(2)比较﹣ ﹣;(填“>”或“<”)
(3)A题:若a=+1,求a2﹣2a+3的值.
B题:若a=,求4a2﹣4a+7的值.
参考答案
一、单项选择题(共30分)
1.解:A、=2,是有理数,故本选项错误;
B、π是无理数,故本选项正确;
C、0.38是有理数,故本选项错误;
D、﹣是有理数,故本选项错误.
故选:B.
2.解:字母B所代表的正方形的面积=169﹣25=144.
故选:C.
3.解:∵冰墩墩在第三象限,
∴盖住的点的坐标可能为(﹣1,﹣2),
故选A.
4.解:A.=4,故此选项不合题意;
B.+无法合并,故此选项不合题意;
C.=,故此选项不合题意;
D.×=,故此选项符合题意.
故选:D.
5.解:∵点P在第四象限内,P到x轴的距离是4,到y轴的距离是3,
∴点P的横坐标为3,纵坐标为﹣4,
∴点P的坐标为(3,﹣4).
故选:A.
6.解:由题意得,AC===,
故可得AM=,BM=AM﹣AB=﹣3,
又∵点B表示的数为2,
∴点M表示的数为﹣1,
故选:C.
7.解:∵32+42=52,
∴该三角形是直角三角形,
故选:D.
8.解:∵葛藤绕树干盘旋2圈升高为2.4m,
∴葛藤绕树干盘旋1圈升高为1.2m,
如图所示:
AC===1.3(m).
∴这段葛藤的长=2×1.3=2.6(m).
故选:C.
9.解:,则1720的平方根为,
故选:D.
10.解:观察发现:P1(0,1)先向左平移1个单位,再向下平移1个单位得到P2(﹣1,0);
P2(﹣1,0)先向右平移1个单位,再向下平移1个单位得到P3(0,﹣1);
P3(0,﹣1)先向右平移2个单位,再向上平移2个单位得到P4(2,1);
P4(2,1)先向左平移3个单位,再向上平移3个单位得到P5(﹣1,4);
P5(﹣1,4)先向左平移5个单位,再向下平移5个单位得到P6(﹣6,﹣1);
P6(﹣6,﹣1)先向右平移8个单位,再向下平移8个单位得到P7(2,﹣9);
故选:D.
二、填空题(共24分)
11.解:﹣27的立方根是﹣3;
0.16的平方根是±=±0.4;
﹣的倒数是:﹣=﹣.
故答案为:﹣3,±0.4,﹣.
12.解:∵点M(m+1,3﹣2m)在y轴上,
∴m+1=0,
∴m=﹣1,
当m=﹣1时,3﹣2m=3﹣2×(﹣1)=3+2=5,
∴点M坐标为(0,5),
故答案为:(0,5).
13.解:建立如下图所示平面直角坐标系:
∴梅山的坐标是(﹣3,6).
故答案为:(﹣3,6).
14.解:∵92+122=152,
∴三角形是直角三角形,
设三角形最长边上的高为hcm,
×9×12=×15×h,
解得:h=7.2,
故答案为:7.2cm.
15.解:根据题意得,
.
故答案为:.
16.解:A题∵点C(﹣1,5)的3级亲密点是点D,
∴点D的坐标为(﹣1+3×5,﹣1×3+5),
即点D的坐标为(14,2),
故答案为:(14,2);
B题:∵点E在x轴上,点E不与原点重合,
∴设点E的坐标为(x,0),
∴OE=|x|,
∵点E的a级亲密点为点F,
∴点F的坐标为(x+a 0,ax+0),
即点F的坐标为(x,ax),
∴EF=|ax|,
∵EF的长度为OE长度的倍,
∴|ax|=|x|,
∴|a|=,
∴a=±,
故答案为:±.
三、解答题(共66分)
17.解:(1)原式=4﹣
=15;
(2)原式=+2﹣+1
=2+2﹣+1
=+3;
(3)x2﹣121=0,
x2=121,
x=±11.
(4)2(x+1)3+16=0.
2(x+1)3=﹣16,
(x+1)3=﹣8,
x+1=﹣2,
x=﹣3.
18.解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2)∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
19.解:(1)学校能听到宣传,
理由:∵学校A到公路MN的距离为800米<1000米,
∴学校能听到宣传;
(2)如图:假设当宣讲车行驶到P点开始影响学校,行驶Q点结束对学校的影响,
则AP=AQ=1000米,AB=800米,
∴BP=BQ==600(米),
∴PQ=1200米,
∴影响学校的时间为:1200÷256=4.6875(分钟),
∴学校A总共能听到4.6875分钟的宣传.
20.解:(1)如图,△ABC即为所求.
△ABC的面积为4×3﹣﹣﹣=4.
故答案为:4.
(2)如图,△A'B'C'即为所求.
由图可得,△A'B'C'与△ABC关于y轴对称.
故答案为:关于y轴对称.
(3)设点P的坐标为(0,m),
∴S△ABP==4,
解得m=5或﹣3.
∴点P的坐标为(0,5)或(0,﹣3).
故答案为:(0,5)或(0,﹣3).
21.解:(1)∵四边形ABCD为矩形,
∴BC=AD=8,∠ABC=90°,
而AB=6,
在Rt△ABC中,AC==10;
(2)∵△ABE沿AE翻折,点B恰好落在对角线AC上的点F处,
∴∠AFE=∠ABE=90°,AF=AB=6,BE=FE,
∴CF=10﹣6=4,
设BE=x,则EF=x,CE=8﹣x,
在Rt△CEF中,x2+42=(8﹣x)2,解得x=3,
∴EB=3,
∴EF=BE=3,
∴S△CEF=×EF×CF=9.
故答案为:9.
22.解:(1)+++…+
=…+
=
=;
(2)=,
=,
∵<,
∴﹣>﹣,
故答案为:>;
(3)A题:∵a=+1,
∴a﹣1=,
∴(a﹣1)2=2,
即a2﹣2a+1=2,
∴a2﹣2a=1,
∴a2﹣2a+3=4,
故答案为:4;
B题:∵a=,
∴a=,
∴2a﹣=1,
∴=1,
即,
∴,
∴4a2﹣4a+7=5,
故答案为:5.
一、单项选择题(共30分)
1.下列实数中是无理数的是( )
A. B.π C.0.38 D.
2.如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是( )
A.12 B.13 C.144 D.194
3.冰墩墩是2022年北京冬季奥运会的吉祥物,将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,深受各国人们的欢迎.在图中,将冰墩墩放入坐标系中,它盖住的点的坐标可能为( )
A.(﹣1,﹣2) B.(﹣1,2) C.(1,2) D.(1,﹣2)
4.下列计算正确的是( )
A. B. C. D.
5.点P在第四象限内,P到x轴的距离是4,到y轴的距离是3,那么点P的坐标( )
A.(3,﹣4) B.(﹣4,3) C.(﹣3,4) D.(4,﹣3)
6.如图,矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对角线AC的长为半径作弧交数轴的正半轴于M,则点M所表示的数为( )
A.2 B.﹣1 C. D.
7.古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距,4个结间距,5个结间距的长度为边长,用木桩钉成一个三角形,其中一角便是直角,这样做的道理是( )
A.直角三角形两个锐角互余 B.三角形的稳定性
C.勾股定理 D.勾股定理的逆定理
8.葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其常绕着附近的树干沿最短路线盘旋而上.现有一段葛藤绕树干盘旋2圈升高为2.4m,如果把树干看成圆柱体,其底面周长是0.5m,如图是葛藤盘旋1圈的示意图,则这段葛藤的长是( )m.
A.1.3 B.2.5 C.2.6 D.2.8
9.,,则1720的平方根为( )
A.13.11 B.±13.11 C.41.47 D.±41.47
10.如图,我们把1,1,2,3,5,8,13,21,…这一列数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°的圆弧P1P2、P2P3、P3P4…,得到斐波那契螺旋线,然后顺次连结P1P2,P2P3,P3P4,得到螺旋折线,已知点P1(0,1)、P2(﹣1,0)、P3(0,﹣1),则该折线上的点P7的坐标为( )
A.(1,﹣9) B.(﹣1,8) C.(2,﹣8) D.(2,﹣9)
二、填空题(本题共24分)
11.﹣27的立方根是 ;0.16的平方根是 ;﹣的倒数是 .
12.点M(m+1,3﹣2m)在y轴上,则点M坐标为 .
13.山西督军府旧址是晋文公重耳庙,历代山西巡抚的衙门设在此.1916年,各省军务长官改称为督军,阎锡山任督军,因此称督军府.督军府主要由门楼、前院、渊谊堂、小自省堂、梅山等组成.如图所示,门楼的坐标是(0,0),渊谊堂的坐标是(0,2),则梅山的坐标是 .
14.一个三角形三条边的长分别是9cm,12cm,15cm,这个三角形最长边上的高为 .
15.某工厂去年的总产值比总支出多500万元,而今年计划的总产值比总支出多950万元,已知今年计划总产值比去年增加15%,而计划总支出比去年减少10%,求去年计划的总产值和总支出各是多少万元?解:设去年计划的总产值、总支出分别是x万元、y万元,根据题意,可列方程组 .
16.在平面直角坐标系中,对于点A(x,y),若点B的坐标为(x+ay,ax+y),则称点B是点A的a级亲密点.例如:点A(﹣2,6)的级亲密点为B(﹣2+×6,×(﹣2)+6),即点B的坐标为(1,5).
A题:已知点C(﹣1,5)的3级亲密点是点D,则点D的坐标为 .
B题:若点E在x轴上,点E不与原点重合,点E的a级亲密点为点F,且EF的长度为OE长度的倍,则a的值= .
三、解答题(共66分)
17.计算:
(1)2+3﹣3.
(2)(﹣)×(﹣)++(3.14﹣π)0.
(3)x2﹣121=0;
(4)2(x+1)3+16=0.
18.已知点P(a﹣2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点Q的坐标为(1,5),直线PQ∥y轴;
(4)点P到x轴、y轴的距离相等.
19.某市创建文明城市,采用移动宣讲的形式进行宣传动员,如图,笔直公路MN的一侧点A处有一学校,学校A到公路MN的距离AB=480米,若宣讲车P周围800米以内能听到广播宣传,宣讲车P在公路MN上延M到N的方向行驶时.
(1)请问学校A能否听到宣传,请说明理由.
(2)如果能听到,已知宣讲车的速度是256米/分,求学校A总共能听到多长时间的宣传.
20.如图所示,在平面直角坐标系中,已知A(0,1)、B(2,0)、C(4,3).
(1)在平面直角坐标系中画出△ABC,则△ABC的面积是 ;
(2)若将点A、B、C的纵坐标不变,横坐标分别乘﹣1,得到△A'B'C',在图中画出△A'B'C',此时△A'B'C'与△ABC的位置关系是 ;
(3)已知P为y轴上一点,若△ABP的面积为4,则点P的坐标是 .
21.如图所示,点E为边BC上一点,将长方形ABCD沿AE折叠,折叠后顶点B恰好落在对角线AC上的点F处,若BC=8,AB=6.
(1)求AC长;
(2)求△CEF的面积.
22.小明在解决问题:已知a=.求2a2﹣8a+1的值,他是这样分析与解的:
∵a===2﹣∴a﹣2=﹣
∴(a﹣2)2=3,a2﹣4a+4=3∴a2﹣4a=﹣1
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1
请你根据小明的分析过程,解决如下问题:
(1)化简+++…+;
(2)比较﹣ ﹣;(填“>”或“<”)
(3)A题:若a=+1,求a2﹣2a+3的值.
B题:若a=,求4a2﹣4a+7的值.
参考答案
一、单项选择题(共30分)
1.解:A、=2,是有理数,故本选项错误;
B、π是无理数,故本选项正确;
C、0.38是有理数,故本选项错误;
D、﹣是有理数,故本选项错误.
故选:B.
2.解:字母B所代表的正方形的面积=169﹣25=144.
故选:C.
3.解:∵冰墩墩在第三象限,
∴盖住的点的坐标可能为(﹣1,﹣2),
故选A.
4.解:A.=4,故此选项不合题意;
B.+无法合并,故此选项不合题意;
C.=,故此选项不合题意;
D.×=,故此选项符合题意.
故选:D.
5.解:∵点P在第四象限内,P到x轴的距离是4,到y轴的距离是3,
∴点P的横坐标为3,纵坐标为﹣4,
∴点P的坐标为(3,﹣4).
故选:A.
6.解:由题意得,AC===,
故可得AM=,BM=AM﹣AB=﹣3,
又∵点B表示的数为2,
∴点M表示的数为﹣1,
故选:C.
7.解:∵32+42=52,
∴该三角形是直角三角形,
故选:D.
8.解:∵葛藤绕树干盘旋2圈升高为2.4m,
∴葛藤绕树干盘旋1圈升高为1.2m,
如图所示:
AC===1.3(m).
∴这段葛藤的长=2×1.3=2.6(m).
故选:C.
9.解:,则1720的平方根为,
故选:D.
10.解:观察发现:P1(0,1)先向左平移1个单位,再向下平移1个单位得到P2(﹣1,0);
P2(﹣1,0)先向右平移1个单位,再向下平移1个单位得到P3(0,﹣1);
P3(0,﹣1)先向右平移2个单位,再向上平移2个单位得到P4(2,1);
P4(2,1)先向左平移3个单位,再向上平移3个单位得到P5(﹣1,4);
P5(﹣1,4)先向左平移5个单位,再向下平移5个单位得到P6(﹣6,﹣1);
P6(﹣6,﹣1)先向右平移8个单位,再向下平移8个单位得到P7(2,﹣9);
故选:D.
二、填空题(共24分)
11.解:﹣27的立方根是﹣3;
0.16的平方根是±=±0.4;
﹣的倒数是:﹣=﹣.
故答案为:﹣3,±0.4,﹣.
12.解:∵点M(m+1,3﹣2m)在y轴上,
∴m+1=0,
∴m=﹣1,
当m=﹣1时,3﹣2m=3﹣2×(﹣1)=3+2=5,
∴点M坐标为(0,5),
故答案为:(0,5).
13.解:建立如下图所示平面直角坐标系:
∴梅山的坐标是(﹣3,6).
故答案为:(﹣3,6).
14.解:∵92+122=152,
∴三角形是直角三角形,
设三角形最长边上的高为hcm,
×9×12=×15×h,
解得:h=7.2,
故答案为:7.2cm.
15.解:根据题意得,
.
故答案为:.
16.解:A题∵点C(﹣1,5)的3级亲密点是点D,
∴点D的坐标为(﹣1+3×5,﹣1×3+5),
即点D的坐标为(14,2),
故答案为:(14,2);
B题:∵点E在x轴上,点E不与原点重合,
∴设点E的坐标为(x,0),
∴OE=|x|,
∵点E的a级亲密点为点F,
∴点F的坐标为(x+a 0,ax+0),
即点F的坐标为(x,ax),
∴EF=|ax|,
∵EF的长度为OE长度的倍,
∴|ax|=|x|,
∴|a|=,
∴a=±,
故答案为:±.
三、解答题(共66分)
17.解:(1)原式=4﹣
=15;
(2)原式=+2﹣+1
=2+2﹣+1
=+3;
(3)x2﹣121=0,
x2=121,
x=±11.
(4)2(x+1)3+16=0.
2(x+1)3=﹣16,
(x+1)3=﹣8,
x+1=﹣2,
x=﹣3.
18.解:(1)∵点P(a﹣2,2a+8),在x轴上,
∴2a+8=0,
解得:a=﹣4,
故a﹣2=﹣4﹣2=﹣6,
则P(﹣6,0);
(2)∵点P(a﹣2,2a+8),在y轴上,
∴a﹣2=0,
解得:a=2,
故2a+8=2×2+8=12,
则P(0,12);
(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,
∴a﹣2=1,
解得:a=3,
故2a+8=14,
则P(1,14);
(4)∵点P到x轴、y轴的距离相等,
∴a﹣2=2a+8或a﹣2+2a+8=0,
解得:a1=﹣10,a2=﹣2,
故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,
则P(﹣12,﹣12);
故当a=﹣2则:a﹣2=﹣4,2a+8=4,
则P(﹣4,4).
综上所述:P(﹣12,﹣12),(﹣4,4).
19.解:(1)学校能听到宣传,
理由:∵学校A到公路MN的距离为800米<1000米,
∴学校能听到宣传;
(2)如图:假设当宣讲车行驶到P点开始影响学校,行驶Q点结束对学校的影响,
则AP=AQ=1000米,AB=800米,
∴BP=BQ==600(米),
∴PQ=1200米,
∴影响学校的时间为:1200÷256=4.6875(分钟),
∴学校A总共能听到4.6875分钟的宣传.
20.解:(1)如图,△ABC即为所求.
△ABC的面积为4×3﹣﹣﹣=4.
故答案为:4.
(2)如图,△A'B'C'即为所求.
由图可得,△A'B'C'与△ABC关于y轴对称.
故答案为:关于y轴对称.
(3)设点P的坐标为(0,m),
∴S△ABP==4,
解得m=5或﹣3.
∴点P的坐标为(0,5)或(0,﹣3).
故答案为:(0,5)或(0,﹣3).
21.解:(1)∵四边形ABCD为矩形,
∴BC=AD=8,∠ABC=90°,
而AB=6,
在Rt△ABC中,AC==10;
(2)∵△ABE沿AE翻折,点B恰好落在对角线AC上的点F处,
∴∠AFE=∠ABE=90°,AF=AB=6,BE=FE,
∴CF=10﹣6=4,
设BE=x,则EF=x,CE=8﹣x,
在Rt△CEF中,x2+42=(8﹣x)2,解得x=3,
∴EB=3,
∴EF=BE=3,
∴S△CEF=×EF×CF=9.
故答案为:9.
22.解:(1)+++…+
=…+
=
=;
(2)=,
=,
∵<,
∴﹣>﹣,
故答案为:>;
(3)A题:∵a=+1,
∴a﹣1=,
∴(a﹣1)2=2,
即a2﹣2a+1=2,
∴a2﹣2a=1,
∴a2﹣2a+3=4,
故答案为:4;
B题:∵a=,
∴a=,
∴2a﹣=1,
∴=1,
即,
∴,
∴4a2﹣4a+7=5,
故答案为:5.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
