2024—2025学年苏科版数学八年级上册期中试题重组练习卷(含详解)
文档属性
| 名称 | 2024—2025学年苏科版数学八年级上册期中试题重组练习卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 457.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览


文档简介
期中试题重组练习卷-2024-2025学年数学八年级上册苏科版
一.选择题(共8小题)
1.(2024秋 凉州区校级期中)根据下列条件不能唯一画出△ABC的是( )
A.AB=5,BC=6,AC=7 B.AB=5,BC=6,∠B=45°
C.AB=5,AC=4,∠C=90° D.AB=5,AC=4,∠C=45°
2.(2022秋 麻阳县期中)如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.1 B. C.2 D.3
3.(2024秋 珠晖区校级期中)如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
A.AB=DC B.OB=OC C.∠C=∠O D.∠AOB=∠DOC
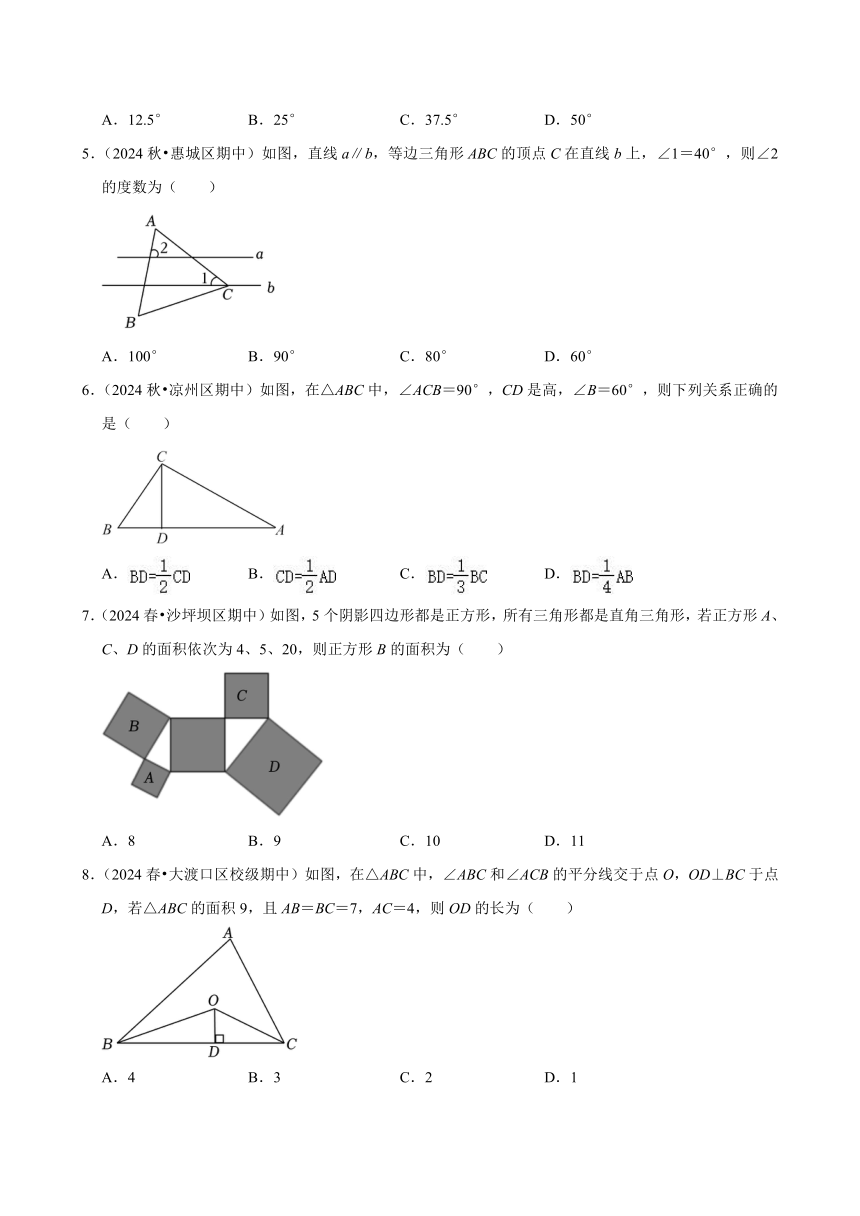
4.(2024秋 献县校级期中)两把相同的长方形直尺按如图所示方式摆放,记两把直尺的接触点为P,其中一把直尺边缘和射线OA重合,另把直尺的下边缘与射线OB重合,连,接OP并延长.若∠BOP=25°,则∠AOP的度数为( )
A.12.5° B.25° C.37.5° D.50°
5.(2024秋 惠城区期中)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠1=40°,则∠2的度数为( )
A.100° B.90° C.80° D.60°
6.(2024秋 凉州区期中)如图,在△ABC中,∠ACB=90°,CD是高,∠B=60°,则下列关系正确的是( )
A. B. C. D.
7.(2024春 沙坪坝区期中)如图,5个阴影四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、5、20,则正方形B的面积为( )
A.8 B.9 C.10 D.11
8.(2024春 大渡口区校级期中)如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于点D,若△ABC的面积9,且AB=BC=7,AC=4,则OD的长为( )
A.4 B.3 C.2 D.1
二.填空题(共8小题)
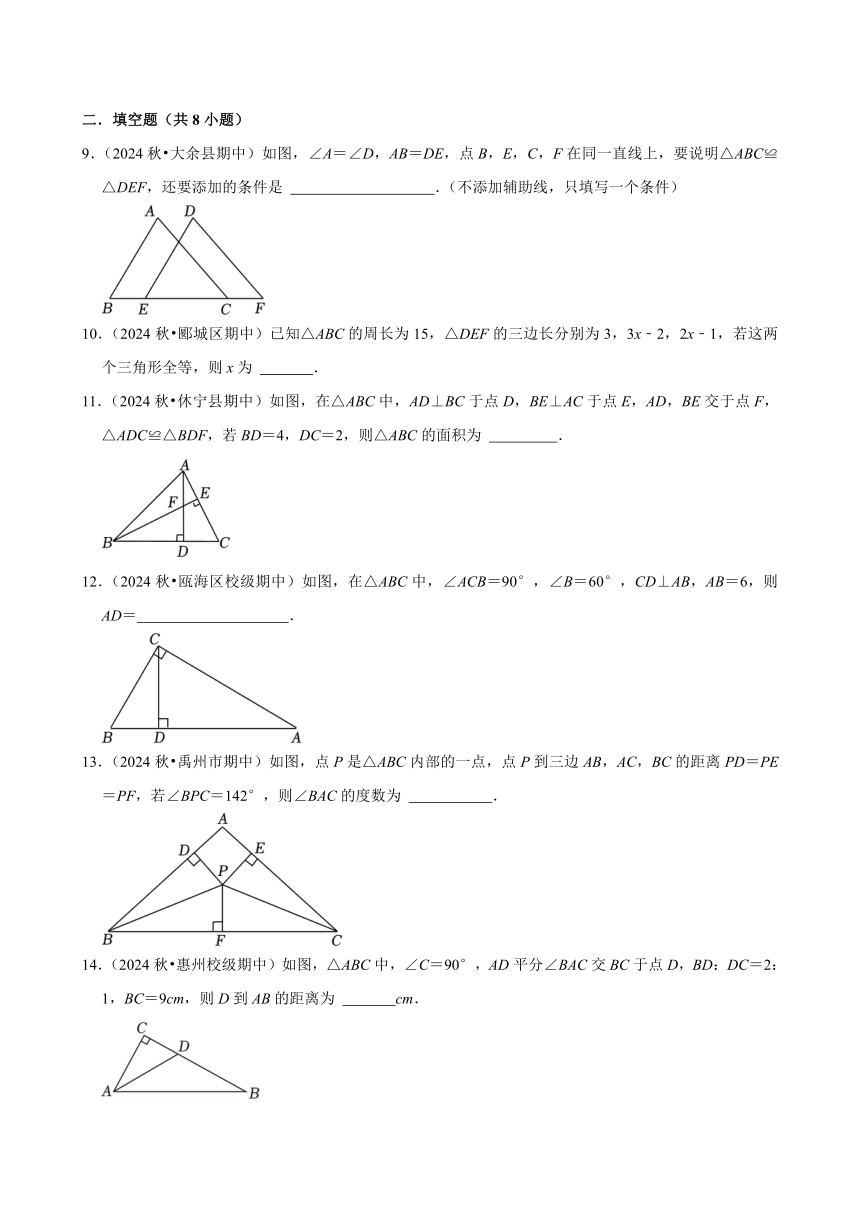
9.(2024秋 大余县期中)如图,∠A=∠D,AB=DE,点B,E,C,F在同一直线上,要说明△ABC≌△DEF,还要添加的条件是 .(不添加辅助线,只填写一个条件)
10.(2024秋 郾城区期中)已知△ABC的周长为15,△DEF的三边长分别为3,3x﹣2,2x﹣1,若这两个三角形全等,则x为 .
11.(2024秋 休宁县期中)如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE交于点F,△ADC≌△BDF,若BD=4,DC=2,则△ABC的面积为 .
12.(2024秋 瓯海区校级期中)如图,在△ABC中,∠ACB=90°,∠B=60°,CD⊥AB,AB=6,则AD= .
13.(2024秋 禹州市期中)如图,点P是△ABC内部的一点,点P到三边AB,AC,BC的距离PD=PE=PF,若∠BPC=142°,则∠BAC的度数为 .
14.(2024秋 惠州校级期中)如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9cm,则D到AB的距离为 cm.
15.(2022秋 无为市期中)如图,一面镜子斜固定在地面OB上,且∠AOB=60°,点P为距离地面OB为8cm的一个光源,光线射出经过镜面D处反射到地面E点,当光线经过的路径长最短为10cm时,PD的长为 .
16.(2024春 沙坪坝区期中)在△ABC中,AC=6,BC=8,AD⊥BC,且AD=3,若点P在直线AC上运动,则BP最短时的值为 .
三.解答题(共8小题)
17.(2024秋 桦甸市校级期中)如图,点F、C在BE上,BF=CE,AB=DE,DF=AC.求证:∠A=∠D.
18.(2024秋 番禺区校级期中)如图,△ADC与△EDG均为等腰直角三角形,连接AG,CE,相交于点H.
(1)求证:AG=CE;
(2)求∠AHE的大小.
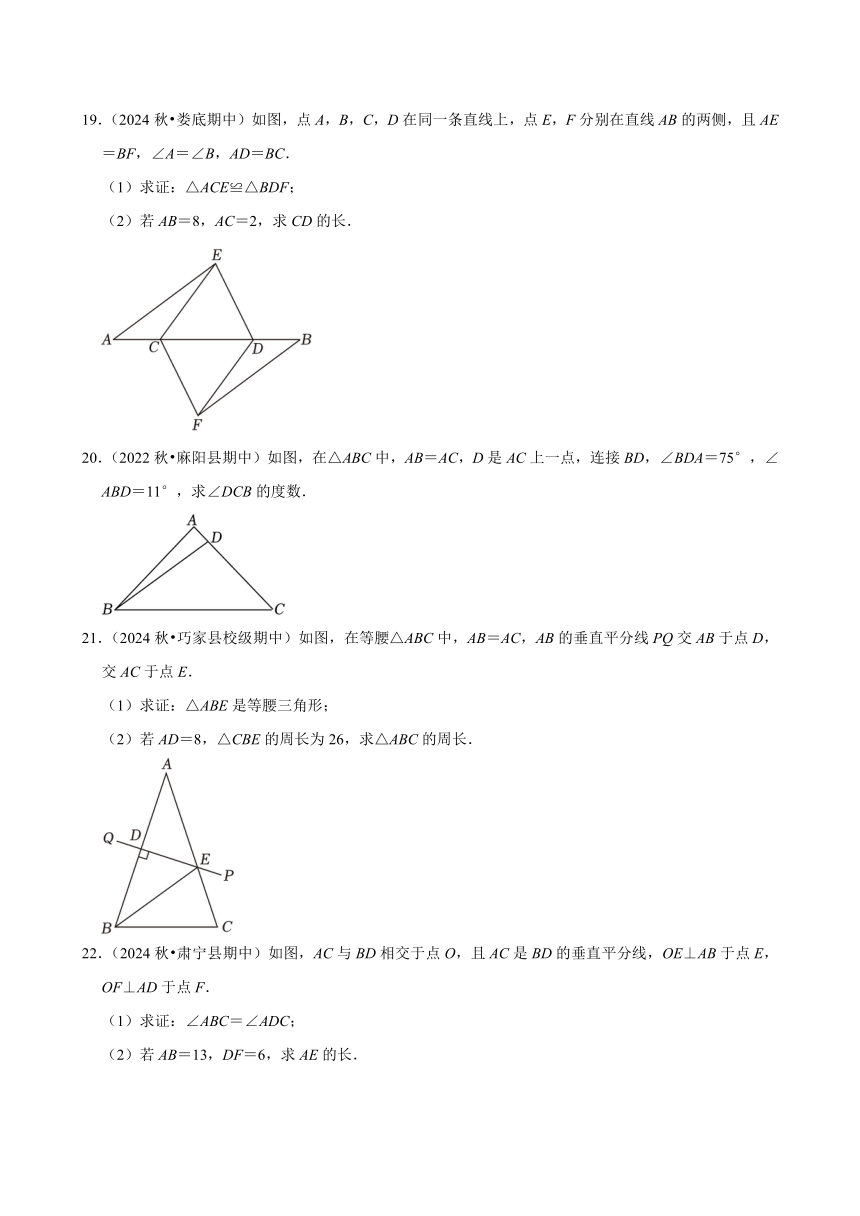
19.(2024秋 娄底期中)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AB的两侧,且AE=BF,∠A=∠B,AD=BC.
(1)求证:△ACE≌△BDF;
(2)若AB=8,AC=2,求CD的长.
20.(2022秋 麻阳县期中)如图,在△ABC中,AB=AC,D是AC上一点,连接BD,∠BDA=75°,∠ABD=11°,求∠DCB的度数.
21.(2024秋 巧家县校级期中)如图,在等腰△ABC中,AB=AC,AB的垂直平分线PQ交AB于点D,交AC于点E.
(1)求证:△ABE是等腰三角形;
(2)若AD=8,△CBE的周长为26,求△ABC的周长.
22.(2024秋 肃宁县期中)如图,AC与BD相交于点O,且AC是BD的垂直平分线,OE⊥AB于点E,OF⊥AD于点F.
(1)求证:∠ABC=∠ADC;
(2)若AB=13,DF=6,求AE的长.
23.(2024秋 江阴市校级期中)如图,点D在△ABC中,∠BDC=90°,AB=13,AC=12,BD=4,CD=3,求图中阴影部分的面积.
24.(2024春 海淀区校级期中)如图①,直角三角形的两条直角边长分别是a,b(a<b),斜边长为c.
(1)探究:用四个这样的直角三角形拼成一大一小两个正方形(如图②).
①小正方形的边长为c,大正方形的边长为 ;
②由大正方形面积的不同表示方式可以得出等式 ,整理得 ,从而验证勾股定理;
(2)应用:将两个这样的直角三角形按图③所示摆放,使BC和CD在一条直线上,连接AE.请你类比(1)中的方法用图③验证勾股定理.
期中试题重组练习卷-2024-2025学年数学八年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 凉州区校级期中)根据下列条件不能唯一画出△ABC的是( )
A.AB=5,BC=6,AC=7 B.AB=5,BC=6,∠B=45°
C.AB=5,AC=4,∠C=90° D.AB=5,AC=4,∠C=45°
【解答】解:A.满足SSS,能唯一画出△ABC,不符合题意;
B.满足SAS,能唯一画出△ABC,不符合题意;
C.满足HL,可唯一画出△ABC,不符合题意;
D.由于是SSA,不能唯一画出△ABC,符合题意.
故选:D.
2.(2022秋 麻阳县期中)如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.1 B. C.2 D.3
【解答】解:∵AD,BE是△ABC的高线,
∴∠ADB=∠ADC=∠AEB=90°,
∵∠BFD=∠AFE,
∴∠DBF=∠CAD,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(ASA),
∴DC=DF,
∵△ACD的面积为12,
∴×CD×6=12,
∴CD=4,
∴DF=4,
∴AF=AD﹣DF=2,
故选:C.
3.(2024秋 珠晖区校级期中)如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
A.AB=DC B.OB=OC C.∠C=∠O D.∠AOB=∠DOC
【解答】解:△AOB和△DOC已经具备OA=OD,∠AOB=∠COD,若添加AB=DC,是满足“两边及其对角对应相等”,不能判定△AOB≌△DOC,故A不正确;
若添加OB=OC,是“两边及其夹角对应相等”,故B正确;
若添加∠C=∠D,是满足“两角及其对边对应相等”,是“AAS”,故C不正确;
添加∠AOB=∠COD,是本身具备的对顶角相等,不能判定△AOB≌△DOC,故D不正确,
故选:B.
4.(2024秋 献县校级期中)两把相同的长方形直尺按如图所示方式摆放,记两把直尺的接触点为P,其中一把直尺边缘和射线OA重合,另把直尺的下边缘与射线OB重合,连,接OP并延长.若∠BOP=25°,则∠AOP的度数为( )
A.12.5° B.25° C.37.5° D.50°
【解答】解:∵两把相同的长方形直尺的宽度一致,
∴点P到射线OA,OB的距离相等,
∴OP是∠AOB的角平分线,
∵∠BOP=25°,
∴∠AOP=∠BOP=25°,
故选:B.
5.(2024秋 惠城区期中)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠1=40°,则∠2的度数为( )
A.100° B.90° C.80° D.60°
【解答】解:设AC与直线a交于D,AB与直线a交于E,如图所示:
∵直线a∥b,∠1=40°,
∴∠ADE=∠1=40°,
∵△ABC为等边三角形,
∴∠A=60°,
∴∠2=180°﹣(∠A+∠ADE)=180°﹣(60°+40°)=80°.
故选:C.
6.(2024秋 凉州区期中)如图,在△ABC中,∠ACB=90°,CD是高,∠B=60°,则下列关系正确的是( )
A. B. C. D.
【解答】解:∵CD是AB边上的高线,
∴CD⊥AB,
∵∠ACB=90°,∠B=60°,
∴∠A=30°,
∵∠B=60°,BC=AB,
∴∠BCD=90°﹣60°=30°,
∴BD=BC,CD=AC,
∴BD=AB.
故选:D.
7.(2024春 沙坪坝区期中)如图,5个阴影四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、5、20,则正方形B的面积为( )
A.8 B.9 C.10 D.11
【解答】解:∵5个阴影四边形都是正方形,所有三角形都是直角三角形,
∴SA+SB=SD﹣SC,
∵正方形A、C、D的面积依次为4、5、20,
∴SB=SD﹣SC﹣SA=20﹣5﹣4=11,
故选:D.
8.(2024春 大渡口区校级期中)如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于点D,若△ABC的面积9,且AB=BC=7,AC=4,则OD的长为( )
A.4 B.3 C.2 D.1
【解答】解:过点O作OE⊥AB,OF⊥AC,垂足分别为E,F,
∵∠ABC和∠ACB的平分线交于点O,
∴OE=OF=OD,
∵△ABC的面积9,且AB=BC=7,AC=4,
∴,
解得OD=1,
故选:D.
二.填空题(共8小题)
9.(2024秋 大余县期中)如图,∠A=∠D,AB=DE,点B,E,C,F在同一直线上,要说明△ABC≌△DEF,还要添加的条件是 AC=DF(答案不唯一) .(不添加辅助线,只填写一个条件)
【解答】解:∵∠A=∠D,AB=DE,
∴添加AC=DF可利用SAS证得△ABC≌△DEF;
添加∠B=∠DEF,可利用ASA证得△ABC≌△DEF;
添加∠ACB=∠DFE,可利用AAS证得△ABC≌△DEF;
故答案为:AC=DF(答案不唯一).
10.(2024秋 郾城区期中)已知△ABC的周长为15,△DEF的三边长分别为3,3x﹣2,2x﹣1,若这两个三角形全等,则x为 3 .
【解答】解:∵两个三角形全等,
∴两三角形的周长相等,
∴3+(3x﹣2)+(2x﹣1)=15,
解得:x=3.
故答案为:3.
11.(2024秋 休宁县期中)如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE交于点F,△ADC≌△BDF,若BD=4,DC=2,则△ABC的面积为 12 .
【解答】解:∵△ADC≌△BDF,
∴AD=BD,
∵BD=4,
∴AD=4,
∵DC=2,
∴BC=BD+DC=4+2=6,
∴.
故答案为:12.
12.(2024秋 瓯海区校级期中)如图,在△ABC中,∠ACB=90°,∠B=60°,CD⊥AB,AB=6,则AD= .
【解答】解:∵∠ACB=90°,∠B=60°,
∴∠A=∠ACB﹣∠B=30°,
∴,
∵CD⊥AB,
∴∠BDC=90°,
∴∠BCD=∠DCB﹣∠B=30°,
∴,
∴,
故答案为:.
13.(2024秋 禹州市期中)如图,点P是△ABC内部的一点,点P到三边AB,AC,BC的距离PD=PE=PF,若∠BPC=142°,则∠BAC的度数为 104° .
【解答】解:∵点P到三边AB,AC,BC的距离PD=PE=PF,
∴BP、CP是∠ABP、∠ACP的角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠PCB,
∵∠BPC=142°,
∴∠PBC+∠PCB=38°,
∴∠ABC+∠ACB=2∠PBC+2∠PCB=2(∠PBC+∠PBC)=76°,
∴∠BAC=180°﹣(∠ABC+∠ACB)=180°﹣76°=104°.
故答案为:104°.
14.(2024秋 惠州校级期中)如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9cm,则D到AB的距离为 3 cm.
【解答】解:过点D作DE⊥AB于E,
∵∠C=90°,
∴AC⊥CD,
∵AD平分∠BAC交BC于点D,
∴CD=DE,
∵BD:DC=2:1,BC=9cm,
∴,
∴CD=DE=3cm,
故答案为:3.
15.(2022秋 无为市期中)如图,一面镜子斜固定在地面OB上,且∠AOB=60°,点P为距离地面OB为8cm的一个光源,光线射出经过镜面D处反射到地面E点,当光线经过的路径长最短为10cm时,PD的长为 4cm .
【解答】解:如图,过点P作OA的对称点P',过点P'作P'E⊥OB于点E,交OA于点D,
则P'E=P'D+DE=PD+DE=10cm,
过点P作PF⊥P'D于F,
∵PC=8cm,
∴EF=PC=8cm,
∴P'F=10﹣8=2(cm),
∵光线射出经过镜面D处反射到地面E点,
∴∠ADP=∠ODE=90°﹣60°=30°,
又∵∠ODE=∠ADP'=30°,
∴∠PDP'=60°,
∴△PDP'是等边三角形,
∴P'F=DF=2cm,
∴PD=P'D=4cm,
故答案为:4cm.
16.(2024春 沙坪坝区期中)在△ABC中,AC=6,BC=8,AD⊥BC,且AD=3,若点P在直线AC上运动,则BP最短时的值为 4 .
【解答】解:当BP⊥AC时,根据垂线段最短,此时BP最小,
∵
∴BC AD=AC BP,
∵AC=6,BC=8,AD=3,
∴8×3=6BP,
∴BP=4,
故答案为:4.
三.解答题(共8小题)
17.(2024秋 桦甸市校级期中)如图,点F、C在BE上,BF=CE,AB=DE,DF=AC.求证:∠A=∠D.
【解答】证明:∵BF=CE,
∴BF+FC=CE+FC,
∴BC=EF,
在△ABC和△DEF中,
∵
∴△ABC≌△DEF(SSS),
∴∠A=∠D.
18.(2024秋 番禺区校级期中)如图,△ADC与△EDG均为等腰直角三角形,连接AG,CE,相交于点H.
(1)求证:AG=CE;
(2)求∠AHE的大小.
【解答】(1)证明:∵△ADC与△EDG均为等腰直角三角形,
∴AD=CD,DG=DE,∠ADC=∠GDE=90°,
∴∠ADC+∠CDG=∠GDE+∠CDG,即∠ADG=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE;
(2)解:设AG与CD交于点B,
∵△ADG≌△CDE,
∴∠DAG=∠DCE,
又∵∠ABD=∠CBH,
∴∠CHB=∠ADB=90°;
∴∠AHE=90°.
19.(2024秋 娄底期中)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AB的两侧,且AE=BF,∠A=∠B,AD=BC.
(1)求证:△ACE≌△BDF;
(2)若AB=8,AC=2,求CD的长.
【解答】(1)证明:∵AD=BC,
∴AD﹣CD=BC﹣CD,即AC=BD,
在△ACE和△BDF中,
,
∴△ACE≌△BDF(SAS);
(2)解:∵△ACE≌△BDF,AC=2,
∴BD=AC=2,
又∵AB=8,
∴CD=AB﹣BD﹣AC=8﹣2﹣2=4.
20.(2022秋 麻阳县期中)如图,在△ABC中,AB=AC,D是AC上一点,连接BD,∠BDA=75°,∠ABD=11°,求∠DCB的度数.
【解答】解:因为∠BDA=75°,∠ABD=11°,
所以∠BAD=180°﹣∠ABD﹣∠BDA=94°,
因为AB=AC.
所以.
21.(2024秋 巧家县校级期中)如图,在等腰△ABC中,AB=AC,AB的垂直平分线PQ交AB于点D,交AC于点E.
(1)求证:△ABE是等腰三角形;
(2)若AD=8,△CBE的周长为26,求△ABC的周长.
【解答】解:(1)∵AB的垂直平分线PQ交AC于点E,
∴EB=EA,
∴△ABE是等腰三角形;
(2)∵AB的垂直平分线PQ交AC于点E,AD=8,
∴AB=2AD=16,
∵△CBE的周长为26,
∴BE+CE+BC=AE+CE+BC=AC+BC=26,
∴△ABC的周长=AB+AC+BC=16+26=42.
22.(2024秋 肃宁县期中)如图,AC与BD相交于点O,且AC是BD的垂直平分线,OE⊥AB于点E,OF⊥AD于点F.
(1)求证:∠ABC=∠ADC;
(2)若AB=13,DF=6,求AE的长.
【解答】(1)证明:∵AC是BD的垂直平分线,
∴AB=AD,CB=CD,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC;
(2)解:由(1)得AB=AD=13,
∵DF=6,
∴AF=AD﹣DF=7,
∵△ABC≌△ADC,
∴∠BAC=∠DAC,
∵OE⊥AB,OF⊥AD,
∴∠AEO=∠AFO=90°,
在△AEO和△AFO中,
,
∴△AEO≌△AFO(AAS),
∴AE=AF=7.
23.(2024秋 江阴市校级期中)如图,点D在△ABC中,∠BDC=90°,AB=13,AC=12,BD=4,CD=3,求图中阴影部分的面积.
【解答】解:∵∠BDC=90°,BD=4,CD=3,
∴BC===5,
∵AB=13,AC=12,
∴AC2+BC2=122+52=169,AB2=132=169,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴∠ACB=90°,
∴图中阴影部分的面积=△ABC的面积﹣△BDC的面积
=AC BC﹣BD CD
=×12×5﹣×3×4
=30﹣6
=24,
∴图中阴影部分的面积为24.
24.(2024春 海淀区校级期中)如图①,直角三角形的两条直角边长分别是a,b(a<b),斜边长为c.
(1)探究:用四个这样的直角三角形拼成一大一小两个正方形(如图②).
①小正方形的边长为c,大正方形的边长为 a+b ;
②由大正方形面积的不同表示方式可以得出等式 ,整理得 a2+b2=c2 ,从而验证勾股定理;
(2)应用:将两个这样的直角三角形按图③所示摆放,使BC和CD在一条直线上,连接AE.请你类比(1)中的方法用图③验证勾股定理.
【解答】解:(1)①由图和题意可知:大正方形的边长为a+b;
故答案为:a+b;
②由大正方形面积的不同表示方式可以得出等式,整理得a2+b2=c2;
故答案为:,a2+b2=c2;
(2)∵∠BAC+∠ACB=90°,∠BAC=∠ECD,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°
用两种不同的方法表示出梯形ABDE的面积,可得:,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
一.选择题(共8小题)
1.(2024秋 凉州区校级期中)根据下列条件不能唯一画出△ABC的是( )
A.AB=5,BC=6,AC=7 B.AB=5,BC=6,∠B=45°
C.AB=5,AC=4,∠C=90° D.AB=5,AC=4,∠C=45°
2.(2022秋 麻阳县期中)如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.1 B. C.2 D.3
3.(2024秋 珠晖区校级期中)如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
A.AB=DC B.OB=OC C.∠C=∠O D.∠AOB=∠DOC
4.(2024秋 献县校级期中)两把相同的长方形直尺按如图所示方式摆放,记两把直尺的接触点为P,其中一把直尺边缘和射线OA重合,另把直尺的下边缘与射线OB重合,连,接OP并延长.若∠BOP=25°,则∠AOP的度数为( )
A.12.5° B.25° C.37.5° D.50°
5.(2024秋 惠城区期中)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠1=40°,则∠2的度数为( )
A.100° B.90° C.80° D.60°
6.(2024秋 凉州区期中)如图,在△ABC中,∠ACB=90°,CD是高,∠B=60°,则下列关系正确的是( )
A. B. C. D.
7.(2024春 沙坪坝区期中)如图,5个阴影四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、5、20,则正方形B的面积为( )
A.8 B.9 C.10 D.11
8.(2024春 大渡口区校级期中)如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于点D,若△ABC的面积9,且AB=BC=7,AC=4,则OD的长为( )
A.4 B.3 C.2 D.1
二.填空题(共8小题)
9.(2024秋 大余县期中)如图,∠A=∠D,AB=DE,点B,E,C,F在同一直线上,要说明△ABC≌△DEF,还要添加的条件是 .(不添加辅助线,只填写一个条件)
10.(2024秋 郾城区期中)已知△ABC的周长为15,△DEF的三边长分别为3,3x﹣2,2x﹣1,若这两个三角形全等,则x为 .
11.(2024秋 休宁县期中)如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE交于点F,△ADC≌△BDF,若BD=4,DC=2,则△ABC的面积为 .
12.(2024秋 瓯海区校级期中)如图,在△ABC中,∠ACB=90°,∠B=60°,CD⊥AB,AB=6,则AD= .
13.(2024秋 禹州市期中)如图,点P是△ABC内部的一点,点P到三边AB,AC,BC的距离PD=PE=PF,若∠BPC=142°,则∠BAC的度数为 .
14.(2024秋 惠州校级期中)如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9cm,则D到AB的距离为 cm.
15.(2022秋 无为市期中)如图,一面镜子斜固定在地面OB上,且∠AOB=60°,点P为距离地面OB为8cm的一个光源,光线射出经过镜面D处反射到地面E点,当光线经过的路径长最短为10cm时,PD的长为 .
16.(2024春 沙坪坝区期中)在△ABC中,AC=6,BC=8,AD⊥BC,且AD=3,若点P在直线AC上运动,则BP最短时的值为 .
三.解答题(共8小题)
17.(2024秋 桦甸市校级期中)如图,点F、C在BE上,BF=CE,AB=DE,DF=AC.求证:∠A=∠D.
18.(2024秋 番禺区校级期中)如图,△ADC与△EDG均为等腰直角三角形,连接AG,CE,相交于点H.
(1)求证:AG=CE;
(2)求∠AHE的大小.
19.(2024秋 娄底期中)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AB的两侧,且AE=BF,∠A=∠B,AD=BC.
(1)求证:△ACE≌△BDF;
(2)若AB=8,AC=2,求CD的长.
20.(2022秋 麻阳县期中)如图,在△ABC中,AB=AC,D是AC上一点,连接BD,∠BDA=75°,∠ABD=11°,求∠DCB的度数.
21.(2024秋 巧家县校级期中)如图,在等腰△ABC中,AB=AC,AB的垂直平分线PQ交AB于点D,交AC于点E.
(1)求证:△ABE是等腰三角形;
(2)若AD=8,△CBE的周长为26,求△ABC的周长.
22.(2024秋 肃宁县期中)如图,AC与BD相交于点O,且AC是BD的垂直平分线,OE⊥AB于点E,OF⊥AD于点F.
(1)求证:∠ABC=∠ADC;
(2)若AB=13,DF=6,求AE的长.
23.(2024秋 江阴市校级期中)如图,点D在△ABC中,∠BDC=90°,AB=13,AC=12,BD=4,CD=3,求图中阴影部分的面积.
24.(2024春 海淀区校级期中)如图①,直角三角形的两条直角边长分别是a,b(a<b),斜边长为c.
(1)探究:用四个这样的直角三角形拼成一大一小两个正方形(如图②).
①小正方形的边长为c,大正方形的边长为 ;
②由大正方形面积的不同表示方式可以得出等式 ,整理得 ,从而验证勾股定理;
(2)应用:将两个这样的直角三角形按图③所示摆放,使BC和CD在一条直线上,连接AE.请你类比(1)中的方法用图③验证勾股定理.
期中试题重组练习卷-2024-2025学年数学八年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 凉州区校级期中)根据下列条件不能唯一画出△ABC的是( )
A.AB=5,BC=6,AC=7 B.AB=5,BC=6,∠B=45°
C.AB=5,AC=4,∠C=90° D.AB=5,AC=4,∠C=45°
【解答】解:A.满足SSS,能唯一画出△ABC,不符合题意;
B.满足SAS,能唯一画出△ABC,不符合题意;
C.满足HL,可唯一画出△ABC,不符合题意;
D.由于是SSA,不能唯一画出△ABC,符合题意.
故选:D.
2.(2022秋 麻阳县期中)如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A.1 B. C.2 D.3
【解答】解:∵AD,BE是△ABC的高线,
∴∠ADB=∠ADC=∠AEB=90°,
∵∠BFD=∠AFE,
∴∠DBF=∠CAD,
在△ACD和△BFD中,
,
∴△ACD≌△BFD(ASA),
∴DC=DF,
∵△ACD的面积为12,
∴×CD×6=12,
∴CD=4,
∴DF=4,
∴AF=AD﹣DF=2,
故选:C.
3.(2024秋 珠晖区校级期中)如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC,还需( )
A.AB=DC B.OB=OC C.∠C=∠O D.∠AOB=∠DOC
【解答】解:△AOB和△DOC已经具备OA=OD,∠AOB=∠COD,若添加AB=DC,是满足“两边及其对角对应相等”,不能判定△AOB≌△DOC,故A不正确;
若添加OB=OC,是“两边及其夹角对应相等”,故B正确;
若添加∠C=∠D,是满足“两角及其对边对应相等”,是“AAS”,故C不正确;
添加∠AOB=∠COD,是本身具备的对顶角相等,不能判定△AOB≌△DOC,故D不正确,
故选:B.
4.(2024秋 献县校级期中)两把相同的长方形直尺按如图所示方式摆放,记两把直尺的接触点为P,其中一把直尺边缘和射线OA重合,另把直尺的下边缘与射线OB重合,连,接OP并延长.若∠BOP=25°,则∠AOP的度数为( )
A.12.5° B.25° C.37.5° D.50°
【解答】解:∵两把相同的长方形直尺的宽度一致,
∴点P到射线OA,OB的距离相等,
∴OP是∠AOB的角平分线,
∵∠BOP=25°,
∴∠AOP=∠BOP=25°,
故选:B.
5.(2024秋 惠城区期中)如图,直线a∥b,等边三角形ABC的顶点C在直线b上,∠1=40°,则∠2的度数为( )
A.100° B.90° C.80° D.60°
【解答】解:设AC与直线a交于D,AB与直线a交于E,如图所示:
∵直线a∥b,∠1=40°,
∴∠ADE=∠1=40°,
∵△ABC为等边三角形,
∴∠A=60°,
∴∠2=180°﹣(∠A+∠ADE)=180°﹣(60°+40°)=80°.
故选:C.
6.(2024秋 凉州区期中)如图,在△ABC中,∠ACB=90°,CD是高,∠B=60°,则下列关系正确的是( )
A. B. C. D.
【解答】解:∵CD是AB边上的高线,
∴CD⊥AB,
∵∠ACB=90°,∠B=60°,
∴∠A=30°,
∵∠B=60°,BC=AB,
∴∠BCD=90°﹣60°=30°,
∴BD=BC,CD=AC,
∴BD=AB.
故选:D.
7.(2024春 沙坪坝区期中)如图,5个阴影四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的面积依次为4、5、20,则正方形B的面积为( )
A.8 B.9 C.10 D.11
【解答】解:∵5个阴影四边形都是正方形,所有三角形都是直角三角形,
∴SA+SB=SD﹣SC,
∵正方形A、C、D的面积依次为4、5、20,
∴SB=SD﹣SC﹣SA=20﹣5﹣4=11,
故选:D.
8.(2024春 大渡口区校级期中)如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,OD⊥BC于点D,若△ABC的面积9,且AB=BC=7,AC=4,则OD的长为( )
A.4 B.3 C.2 D.1
【解答】解:过点O作OE⊥AB,OF⊥AC,垂足分别为E,F,
∵∠ABC和∠ACB的平分线交于点O,
∴OE=OF=OD,
∵△ABC的面积9,且AB=BC=7,AC=4,
∴,
解得OD=1,
故选:D.
二.填空题(共8小题)
9.(2024秋 大余县期中)如图,∠A=∠D,AB=DE,点B,E,C,F在同一直线上,要说明△ABC≌△DEF,还要添加的条件是 AC=DF(答案不唯一) .(不添加辅助线,只填写一个条件)
【解答】解:∵∠A=∠D,AB=DE,
∴添加AC=DF可利用SAS证得△ABC≌△DEF;
添加∠B=∠DEF,可利用ASA证得△ABC≌△DEF;
添加∠ACB=∠DFE,可利用AAS证得△ABC≌△DEF;
故答案为:AC=DF(答案不唯一).
10.(2024秋 郾城区期中)已知△ABC的周长为15,△DEF的三边长分别为3,3x﹣2,2x﹣1,若这两个三角形全等,则x为 3 .
【解答】解:∵两个三角形全等,
∴两三角形的周长相等,
∴3+(3x﹣2)+(2x﹣1)=15,
解得:x=3.
故答案为:3.
11.(2024秋 休宁县期中)如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE交于点F,△ADC≌△BDF,若BD=4,DC=2,则△ABC的面积为 12 .
【解答】解:∵△ADC≌△BDF,
∴AD=BD,
∵BD=4,
∴AD=4,
∵DC=2,
∴BC=BD+DC=4+2=6,
∴.
故答案为:12.
12.(2024秋 瓯海区校级期中)如图,在△ABC中,∠ACB=90°,∠B=60°,CD⊥AB,AB=6,则AD= .
【解答】解:∵∠ACB=90°,∠B=60°,
∴∠A=∠ACB﹣∠B=30°,
∴,
∵CD⊥AB,
∴∠BDC=90°,
∴∠BCD=∠DCB﹣∠B=30°,
∴,
∴,
故答案为:.
13.(2024秋 禹州市期中)如图,点P是△ABC内部的一点,点P到三边AB,AC,BC的距离PD=PE=PF,若∠BPC=142°,则∠BAC的度数为 104° .
【解答】解:∵点P到三边AB,AC,BC的距离PD=PE=PF,
∴BP、CP是∠ABP、∠ACP的角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠PCB,
∵∠BPC=142°,
∴∠PBC+∠PCB=38°,
∴∠ABC+∠ACB=2∠PBC+2∠PCB=2(∠PBC+∠PBC)=76°,
∴∠BAC=180°﹣(∠ABC+∠ACB)=180°﹣76°=104°.
故答案为:104°.
14.(2024秋 惠州校级期中)如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BD:DC=2:1,BC=9cm,则D到AB的距离为 3 cm.
【解答】解:过点D作DE⊥AB于E,
∵∠C=90°,
∴AC⊥CD,
∵AD平分∠BAC交BC于点D,
∴CD=DE,
∵BD:DC=2:1,BC=9cm,
∴,
∴CD=DE=3cm,
故答案为:3.
15.(2022秋 无为市期中)如图,一面镜子斜固定在地面OB上,且∠AOB=60°,点P为距离地面OB为8cm的一个光源,光线射出经过镜面D处反射到地面E点,当光线经过的路径长最短为10cm时,PD的长为 4cm .
【解答】解:如图,过点P作OA的对称点P',过点P'作P'E⊥OB于点E,交OA于点D,
则P'E=P'D+DE=PD+DE=10cm,
过点P作PF⊥P'D于F,
∵PC=8cm,
∴EF=PC=8cm,
∴P'F=10﹣8=2(cm),
∵光线射出经过镜面D处反射到地面E点,
∴∠ADP=∠ODE=90°﹣60°=30°,
又∵∠ODE=∠ADP'=30°,
∴∠PDP'=60°,
∴△PDP'是等边三角形,
∴P'F=DF=2cm,
∴PD=P'D=4cm,
故答案为:4cm.
16.(2024春 沙坪坝区期中)在△ABC中,AC=6,BC=8,AD⊥BC,且AD=3,若点P在直线AC上运动,则BP最短时的值为 4 .
【解答】解:当BP⊥AC时,根据垂线段最短,此时BP最小,
∵
∴BC AD=AC BP,
∵AC=6,BC=8,AD=3,
∴8×3=6BP,
∴BP=4,
故答案为:4.
三.解答题(共8小题)
17.(2024秋 桦甸市校级期中)如图,点F、C在BE上,BF=CE,AB=DE,DF=AC.求证:∠A=∠D.
【解答】证明:∵BF=CE,
∴BF+FC=CE+FC,
∴BC=EF,
在△ABC和△DEF中,
∵
∴△ABC≌△DEF(SSS),
∴∠A=∠D.
18.(2024秋 番禺区校级期中)如图,△ADC与△EDG均为等腰直角三角形,连接AG,CE,相交于点H.
(1)求证:AG=CE;
(2)求∠AHE的大小.
【解答】(1)证明:∵△ADC与△EDG均为等腰直角三角形,
∴AD=CD,DG=DE,∠ADC=∠GDE=90°,
∴∠ADC+∠CDG=∠GDE+∠CDG,即∠ADG=∠CDE,
∴△ADG≌△CDE(SAS),
∴AG=CE;
(2)解:设AG与CD交于点B,
∵△ADG≌△CDE,
∴∠DAG=∠DCE,
又∵∠ABD=∠CBH,
∴∠CHB=∠ADB=90°;
∴∠AHE=90°.
19.(2024秋 娄底期中)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AB的两侧,且AE=BF,∠A=∠B,AD=BC.
(1)求证:△ACE≌△BDF;
(2)若AB=8,AC=2,求CD的长.
【解答】(1)证明:∵AD=BC,
∴AD﹣CD=BC﹣CD,即AC=BD,
在△ACE和△BDF中,
,
∴△ACE≌△BDF(SAS);
(2)解:∵△ACE≌△BDF,AC=2,
∴BD=AC=2,
又∵AB=8,
∴CD=AB﹣BD﹣AC=8﹣2﹣2=4.
20.(2022秋 麻阳县期中)如图,在△ABC中,AB=AC,D是AC上一点,连接BD,∠BDA=75°,∠ABD=11°,求∠DCB的度数.
【解答】解:因为∠BDA=75°,∠ABD=11°,
所以∠BAD=180°﹣∠ABD﹣∠BDA=94°,
因为AB=AC.
所以.
21.(2024秋 巧家县校级期中)如图,在等腰△ABC中,AB=AC,AB的垂直平分线PQ交AB于点D,交AC于点E.
(1)求证:△ABE是等腰三角形;
(2)若AD=8,△CBE的周长为26,求△ABC的周长.
【解答】解:(1)∵AB的垂直平分线PQ交AC于点E,
∴EB=EA,
∴△ABE是等腰三角形;
(2)∵AB的垂直平分线PQ交AC于点E,AD=8,
∴AB=2AD=16,
∵△CBE的周长为26,
∴BE+CE+BC=AE+CE+BC=AC+BC=26,
∴△ABC的周长=AB+AC+BC=16+26=42.
22.(2024秋 肃宁县期中)如图,AC与BD相交于点O,且AC是BD的垂直平分线,OE⊥AB于点E,OF⊥AD于点F.
(1)求证:∠ABC=∠ADC;
(2)若AB=13,DF=6,求AE的长.
【解答】(1)证明:∵AC是BD的垂直平分线,
∴AB=AD,CB=CD,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC;
(2)解:由(1)得AB=AD=13,
∵DF=6,
∴AF=AD﹣DF=7,
∵△ABC≌△ADC,
∴∠BAC=∠DAC,
∵OE⊥AB,OF⊥AD,
∴∠AEO=∠AFO=90°,
在△AEO和△AFO中,
,
∴△AEO≌△AFO(AAS),
∴AE=AF=7.
23.(2024秋 江阴市校级期中)如图,点D在△ABC中,∠BDC=90°,AB=13,AC=12,BD=4,CD=3,求图中阴影部分的面积.
【解答】解:∵∠BDC=90°,BD=4,CD=3,
∴BC===5,
∵AB=13,AC=12,
∴AC2+BC2=122+52=169,AB2=132=169,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴∠ACB=90°,
∴图中阴影部分的面积=△ABC的面积﹣△BDC的面积
=AC BC﹣BD CD
=×12×5﹣×3×4
=30﹣6
=24,
∴图中阴影部分的面积为24.
24.(2024春 海淀区校级期中)如图①,直角三角形的两条直角边长分别是a,b(a<b),斜边长为c.
(1)探究:用四个这样的直角三角形拼成一大一小两个正方形(如图②).
①小正方形的边长为c,大正方形的边长为 a+b ;
②由大正方形面积的不同表示方式可以得出等式 ,整理得 a2+b2=c2 ,从而验证勾股定理;
(2)应用:将两个这样的直角三角形按图③所示摆放,使BC和CD在一条直线上,连接AE.请你类比(1)中的方法用图③验证勾股定理.
【解答】解:(1)①由图和题意可知:大正方形的边长为a+b;
故答案为:a+b;
②由大正方形面积的不同表示方式可以得出等式,整理得a2+b2=c2;
故答案为:,a2+b2=c2;
(2)∵∠BAC+∠ACB=90°,∠BAC=∠ECD,
∴∠ECD+∠ACB=90°,
∴∠ACE=90°
用两种不同的方法表示出梯形ABDE的面积,可得:,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
同课章节目录
