2024-2025学年人教版数学八年级上册期中复习试卷(第11,12,13章)(含答案)
文档属性
| 名称 | 2024-2025学年人教版数学八年级上册期中复习试卷(第11,12,13章)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 533.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 16:03:24 | ||
图片预览

文档简介
2024-2025学年人教版数学八年级上册期中复习试卷(第11,12,13章)
一、单选题(共10题;共30分)
1.(3分)以下面四组小棒为边长,能围成三角形的是( )组.
A.4,7,3 B.4,7,4 C.4,7,11 D.4,7,12
2.(3分)如图,用纸板挡住部分三角形后,能用尺规画出与此三角形全等的三角形,其全等的依据是( )
A. B. C. D.
3.(3分)已知△ABC的三个内角满足:∠A=∠B=∠C,则此三角形是( )
A.等腰三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
4.(3分)以下列线段为边不能组成等腰三角形的是( )
A.2,2,4 B.6,3,6 C.4,4,5 D.1,1,1
5.(3分)如图, ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
A.10 B.8 C.6 D.4
6.(3分)如图,等边和等腰,,点E,F分别为边,的中点,若的面积为16,,点M是CE上的动点,则的周长的最小值为( )
A.6 B.8 C.9 D.10
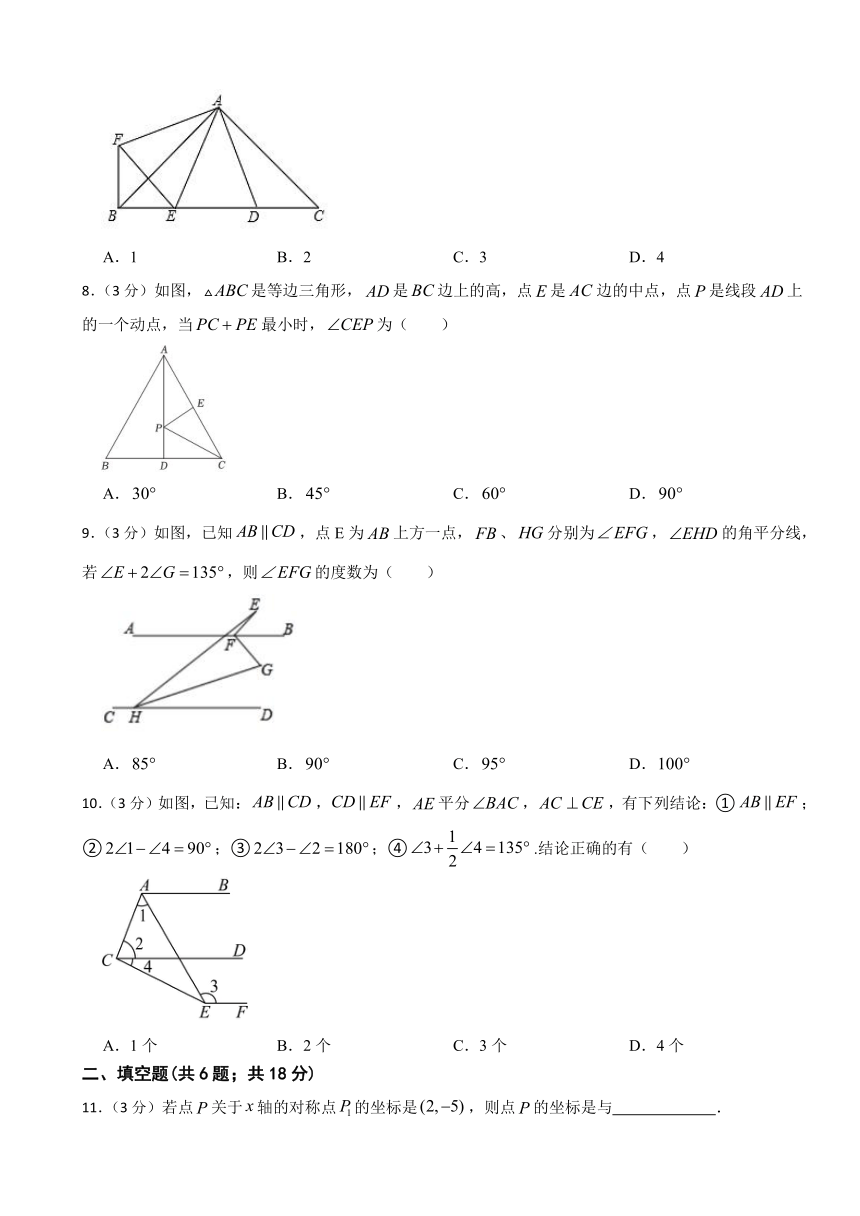
7.(3分)如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△AED为等腰三角形
③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个
A.1 B.2 C.3 D.4
8.(3分)如图,是等边三角形,是边上的高,点是边的中点,点是线段上的一个动点,当最小时,为( )
A. B. C. D.
9.(3分)如图,已知,点E为上方一点,、分别为,的角平分线,若,则的度数为( )
A. B. C. D.
10.(3分)如图,已知:,,平分,,有下列结论:①;②;③;④.结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6题;共18分)
11.(3分)若点关于轴的对称点的坐标是,则点的坐标是与 .
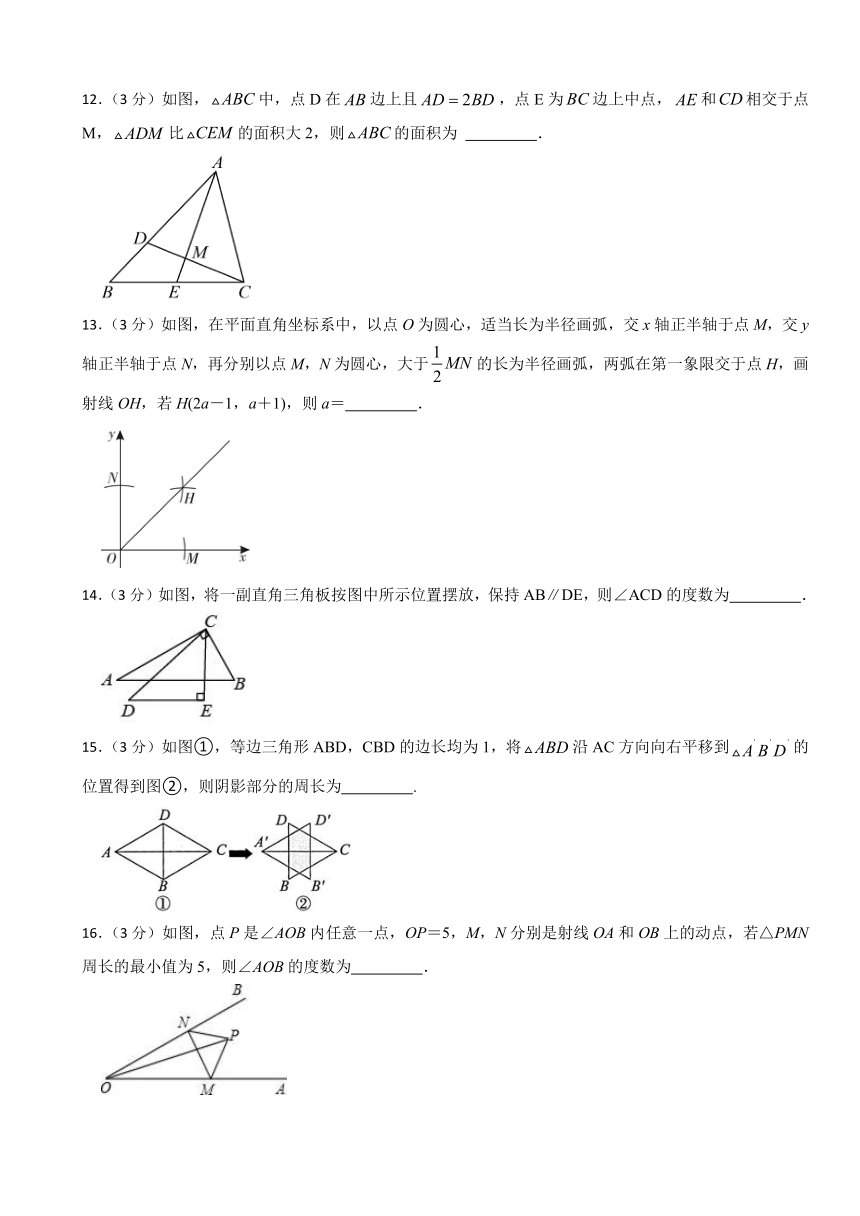
12.(3分)如图,中,点D在边上且,点E为边上中点,和相交于点M,比的面积大2,则的面积为 .
13.(3分)如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴正半轴于点M,交y轴正半轴于点N,再分别以点M,N为圆心,大于的长为半径画弧,两弧在第一象限交于点H,画射线OH,若H(2a-1,a+1),则a= .
14.(3分)如图,将一副直角三角板按图中所示位置摆放,保持AB∥DE,则∠ACD的度数为 .
15.(3分)如图①,等边三角形ABD,CBD的边长均为1,将沿AC方向向右平移到的位置得到图②,则阴影部分的周长为 .
16.(3分)如图,点P是∠AOB内任意一点,OP=5,M,N分别是射线OA和OB上的动点,若△PMN周长的最小值为5,则∠AOB的度数为 .
三、解答题(共6题;共52分)
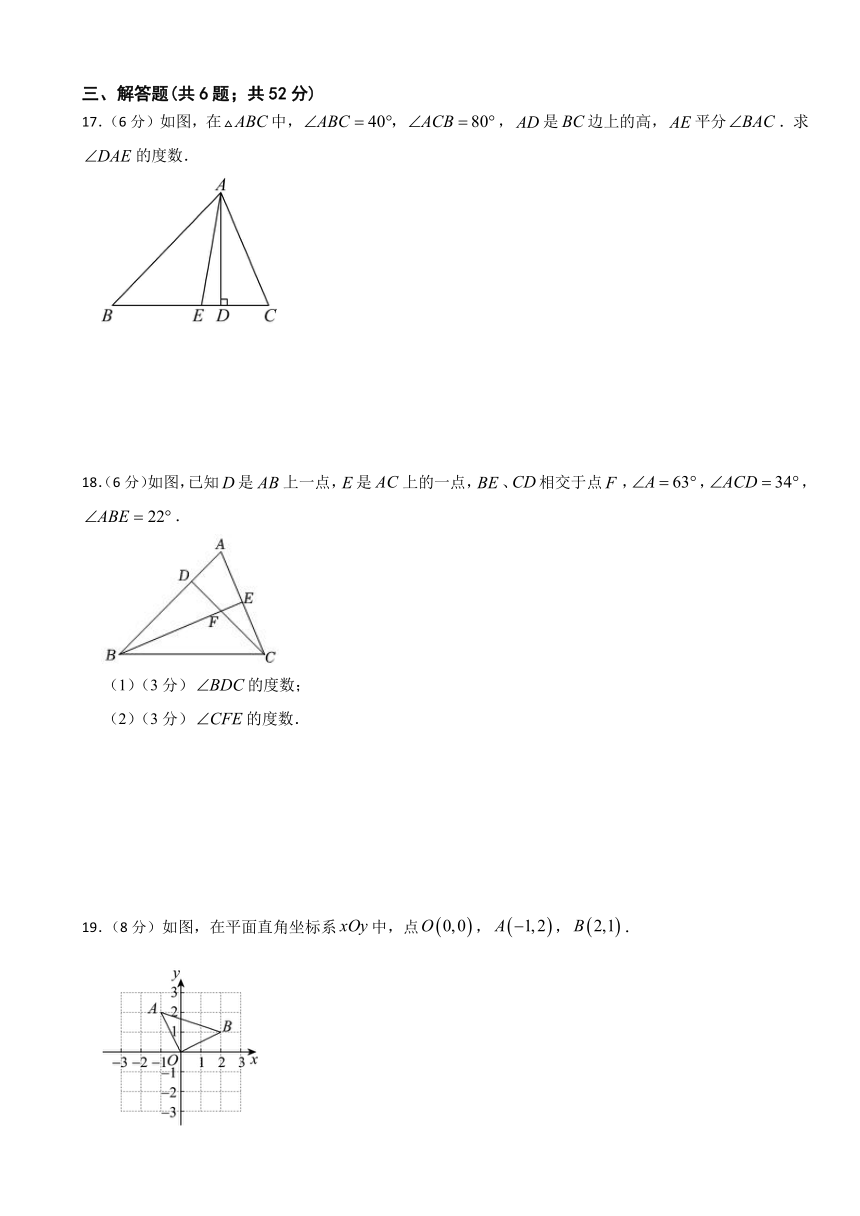
17.(6分)如图,在中,,是边上的高,平分.求的度数.
18.(6分)如图,已知是上一点,是上的一点,、相交于点,,,.
(1)(3分)的度数;
(2)(3分)的度数.
19.(8分)如图,在平面直角坐标系中,点,,.
(1)(4分)在图中商出关于x轴对称的,并直接写出点,的坐标;
(2)(4分)直接写出的面积为___________.
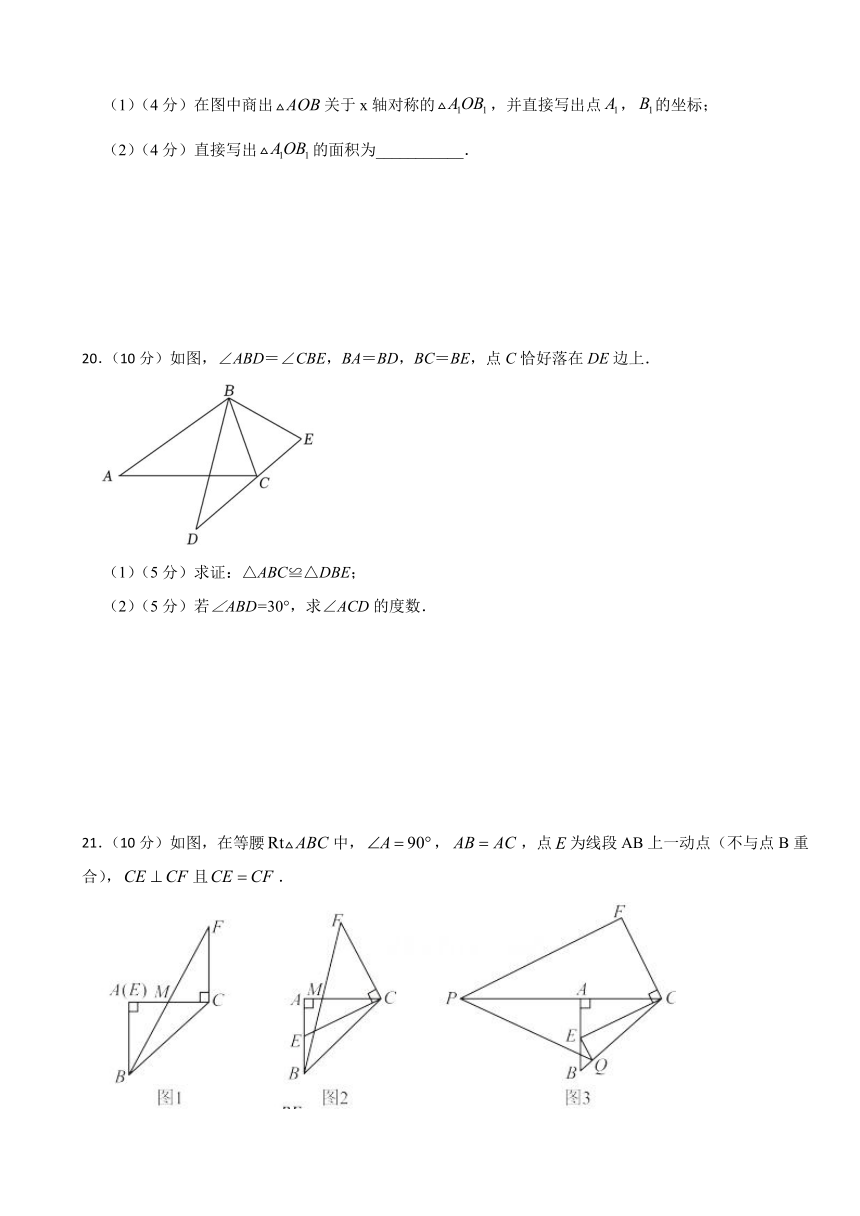
20.(10分)如图,∠ABD=∠CBE,BA=BD,BC=BE,点C恰好落在DE边上.
(1)(5分)求证:△ABC≌△DBE;
(2)(5分)若∠ABD=30°,求∠ACD的度数.
21.(10分)如图,在等腰中,,,点为线段AB上一动点(不与点B重合),且.
(1)(5分)连接BF交AC于点,设.
①当时,如图1,则 ▲ .
②当时,如图2,若,求MC的长.
(2)(5分)如图3,作交CA的延长线于点,交BC于点,连接PQ,求证:.
22.(12分)如图1,在平面直角坐标系内,直线与轴正半轴交于点,与轴正半轴交于点,点是轴负半轴上一点,点是直线上位于第四象限内的一点,直线经过原点,且平分,的平分线与直线交于点,的平分线与直线交于点.
(1)(4分)判断与的位置关系,并说明理由;
(2)(4分)在,,中,如果有一个角是另一个角的4倍,直接写出的度数:__________;
(3)(4分)如图2,当取(2)结论中的最大值时,过点作交直线于点,点是直线上一点且,现将绕点逆时针旋转度,得到,射线交直线于点,的平分线交直线于点,在旋转过程中,是否存在,使得,若存在,请直线写出的值;若不存在,请说明理由.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】D
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】D
11.【答案】(2,5)
12.【答案】12
13.【答案】2
14.【答案】15°
15.【答案】2
16.【答案】30°.
17.【答案】
18.【答案】(1)解:,,
(2)解:由得,
,
,
.
19.【答案】(1)解:画出的如下图所示:
则,的坐标分别为,;
(2)
20.【答案】(1)∵∠ABD=∠CBE
∴∠ABC=∠DBE
在△ABC和△DBE中
∴△ABC≌△DBE(SAS).
(2)∵△ABC≌△DBE
∴∠ABC=∠DBE
又∵∠ABC=∠ABD+∠CBD,∠DBE=∠EBC+∠CBD
∴∠ABD=∠EBC=30°
∵BC=BE
∴∠BCE=∠E=70°
又∵△ABC≌△DBE
∴∠ACB=∠BED=70°
∴∠ACD=180°-∠BCE-∠ACB=180°-70°-70°=40°.
21.【答案】(1)解:①△ABC中,∠A=90°,AB=AC,CE⊥CF,CE=CF,
∴AB=AC=CE=CF,∠BAM=∠FCM=90°,
在△ABM与△CFM中,
,
∴△ABM≌△CFM(AAS),
∴BM=MF,
∴,
故答案为:1;
②过点F作FN⊥AC于N,如图:
设BE=4a,则AB=9a,AE=AB-BE=5a,
又∵∠A=90°,CE⊥CF,
∴∠FNC=∠CAE=90°,∠ACE+∠AEC=90°,∠ACE+∠ACF=90°,
∴∠AEC=∠NCF,
在△ACE和△NFC中,
,
∴△ACE≌△NFC(AAS),
∴CN=AE=5a,FN=AC=AB=9a,
∴AN=9a-5a=4a,
在△ABM和△FNM中,
,
∴△ABM≌△FNM(AAS),
∴AM=NM=2a,
∴MC=7a,
∵AB=9a=18,
∴a=2,
∴MC=7a=14.
(2)证明:在FP上截取FG=EQ,连接CG、PQ,如图:
在△CFG和△CEQ中,
,
∴△CFG≌△CEQ(SAS),
∴∠FCG=∠ECQ,CG=CQ,
∵∠FCG+∠GCE=90°,
∴∠ECQ+∠GCE=90°,
∵∠ACB=45°,
∴∠PCG=∠PCQ=45°,
在△PCG和△PCQ中,
,
∴△PCG≌△PCQ(SAS),
∴PQ=PG,
∵PG=PF-GF=PF-QE,
∴PQ=PF-QE.
22.【答案】(1)
(2)或
(3)存在,或
一、单选题(共10题;共30分)
1.(3分)以下面四组小棒为边长,能围成三角形的是( )组.
A.4,7,3 B.4,7,4 C.4,7,11 D.4,7,12
2.(3分)如图,用纸板挡住部分三角形后,能用尺规画出与此三角形全等的三角形,其全等的依据是( )
A. B. C. D.
3.(3分)已知△ABC的三个内角满足:∠A=∠B=∠C,则此三角形是( )
A.等腰三角形 B.锐角三角形 C.直角三角形 D.钝角三角形
4.(3分)以下列线段为边不能组成等腰三角形的是( )
A.2,2,4 B.6,3,6 C.4,4,5 D.1,1,1
5.(3分)如图, ABCD的周长为20,AE平分∠BAD,若CE=2,则AB的长度是( )
A.10 B.8 C.6 D.4
6.(3分)如图,等边和等腰,,点E,F分别为边,的中点,若的面积为16,,点M是CE上的动点,则的周长的最小值为( )
A.6 B.8 C.9 D.10
7.(3分)如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△AED为等腰三角形
③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个
A.1 B.2 C.3 D.4
8.(3分)如图,是等边三角形,是边上的高,点是边的中点,点是线段上的一个动点,当最小时,为( )
A. B. C. D.
9.(3分)如图,已知,点E为上方一点,、分别为,的角平分线,若,则的度数为( )
A. B. C. D.
10.(3分)如图,已知:,,平分,,有下列结论:①;②;③;④.结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6题;共18分)
11.(3分)若点关于轴的对称点的坐标是,则点的坐标是与 .
12.(3分)如图,中,点D在边上且,点E为边上中点,和相交于点M,比的面积大2,则的面积为 .
13.(3分)如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴正半轴于点M,交y轴正半轴于点N,再分别以点M,N为圆心,大于的长为半径画弧,两弧在第一象限交于点H,画射线OH,若H(2a-1,a+1),则a= .
14.(3分)如图,将一副直角三角板按图中所示位置摆放,保持AB∥DE,则∠ACD的度数为 .
15.(3分)如图①,等边三角形ABD,CBD的边长均为1,将沿AC方向向右平移到的位置得到图②,则阴影部分的周长为 .
16.(3分)如图,点P是∠AOB内任意一点,OP=5,M,N分别是射线OA和OB上的动点,若△PMN周长的最小值为5,则∠AOB的度数为 .
三、解答题(共6题;共52分)
17.(6分)如图,在中,,是边上的高,平分.求的度数.
18.(6分)如图,已知是上一点,是上的一点,、相交于点,,,.
(1)(3分)的度数;
(2)(3分)的度数.
19.(8分)如图,在平面直角坐标系中,点,,.
(1)(4分)在图中商出关于x轴对称的,并直接写出点,的坐标;
(2)(4分)直接写出的面积为___________.
20.(10分)如图,∠ABD=∠CBE,BA=BD,BC=BE,点C恰好落在DE边上.
(1)(5分)求证:△ABC≌△DBE;
(2)(5分)若∠ABD=30°,求∠ACD的度数.
21.(10分)如图,在等腰中,,,点为线段AB上一动点(不与点B重合),且.
(1)(5分)连接BF交AC于点,设.
①当时,如图1,则 ▲ .
②当时,如图2,若,求MC的长.
(2)(5分)如图3,作交CA的延长线于点,交BC于点,连接PQ,求证:.
22.(12分)如图1,在平面直角坐标系内,直线与轴正半轴交于点,与轴正半轴交于点,点是轴负半轴上一点,点是直线上位于第四象限内的一点,直线经过原点,且平分,的平分线与直线交于点,的平分线与直线交于点.
(1)(4分)判断与的位置关系,并说明理由;
(2)(4分)在,,中,如果有一个角是另一个角的4倍,直接写出的度数:__________;
(3)(4分)如图2,当取(2)结论中的最大值时,过点作交直线于点,点是直线上一点且,现将绕点逆时针旋转度,得到,射线交直线于点,的平分线交直线于点,在旋转过程中,是否存在,使得,若存在,请直线写出的值;若不存在,请说明理由.
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】D
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】D
11.【答案】(2,5)
12.【答案】12
13.【答案】2
14.【答案】15°
15.【答案】2
16.【答案】30°.
17.【答案】
18.【答案】(1)解:,,
(2)解:由得,
,
,
.
19.【答案】(1)解:画出的如下图所示:
则,的坐标分别为,;
(2)
20.【答案】(1)∵∠ABD=∠CBE
∴∠ABC=∠DBE
在△ABC和△DBE中
∴△ABC≌△DBE(SAS).
(2)∵△ABC≌△DBE
∴∠ABC=∠DBE
又∵∠ABC=∠ABD+∠CBD,∠DBE=∠EBC+∠CBD
∴∠ABD=∠EBC=30°
∵BC=BE
∴∠BCE=∠E=70°
又∵△ABC≌△DBE
∴∠ACB=∠BED=70°
∴∠ACD=180°-∠BCE-∠ACB=180°-70°-70°=40°.
21.【答案】(1)解:①△ABC中,∠A=90°,AB=AC,CE⊥CF,CE=CF,
∴AB=AC=CE=CF,∠BAM=∠FCM=90°,
在△ABM与△CFM中,
,
∴△ABM≌△CFM(AAS),
∴BM=MF,
∴,
故答案为:1;
②过点F作FN⊥AC于N,如图:
设BE=4a,则AB=9a,AE=AB-BE=5a,
又∵∠A=90°,CE⊥CF,
∴∠FNC=∠CAE=90°,∠ACE+∠AEC=90°,∠ACE+∠ACF=90°,
∴∠AEC=∠NCF,
在△ACE和△NFC中,
,
∴△ACE≌△NFC(AAS),
∴CN=AE=5a,FN=AC=AB=9a,
∴AN=9a-5a=4a,
在△ABM和△FNM中,
,
∴△ABM≌△FNM(AAS),
∴AM=NM=2a,
∴MC=7a,
∵AB=9a=18,
∴a=2,
∴MC=7a=14.
(2)证明:在FP上截取FG=EQ,连接CG、PQ,如图:
在△CFG和△CEQ中,
,
∴△CFG≌△CEQ(SAS),
∴∠FCG=∠ECQ,CG=CQ,
∵∠FCG+∠GCE=90°,
∴∠ECQ+∠GCE=90°,
∵∠ACB=45°,
∴∠PCG=∠PCQ=45°,
在△PCG和△PCQ中,
,
∴△PCG≌△PCQ(SAS),
∴PQ=PG,
∵PG=PF-GF=PF-QE,
∴PQ=PF-QE.
22.【答案】(1)
(2)或
(3)存在,或
同课章节目录
