第二十二章二次函数 单元练习(含答案) 2024—2025学年人教版九年级数学上册
文档属性
| 名称 | 第二十二章二次函数 单元练习(含答案) 2024—2025学年人教版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 701.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 15:55:44 | ||
图片预览


文档简介
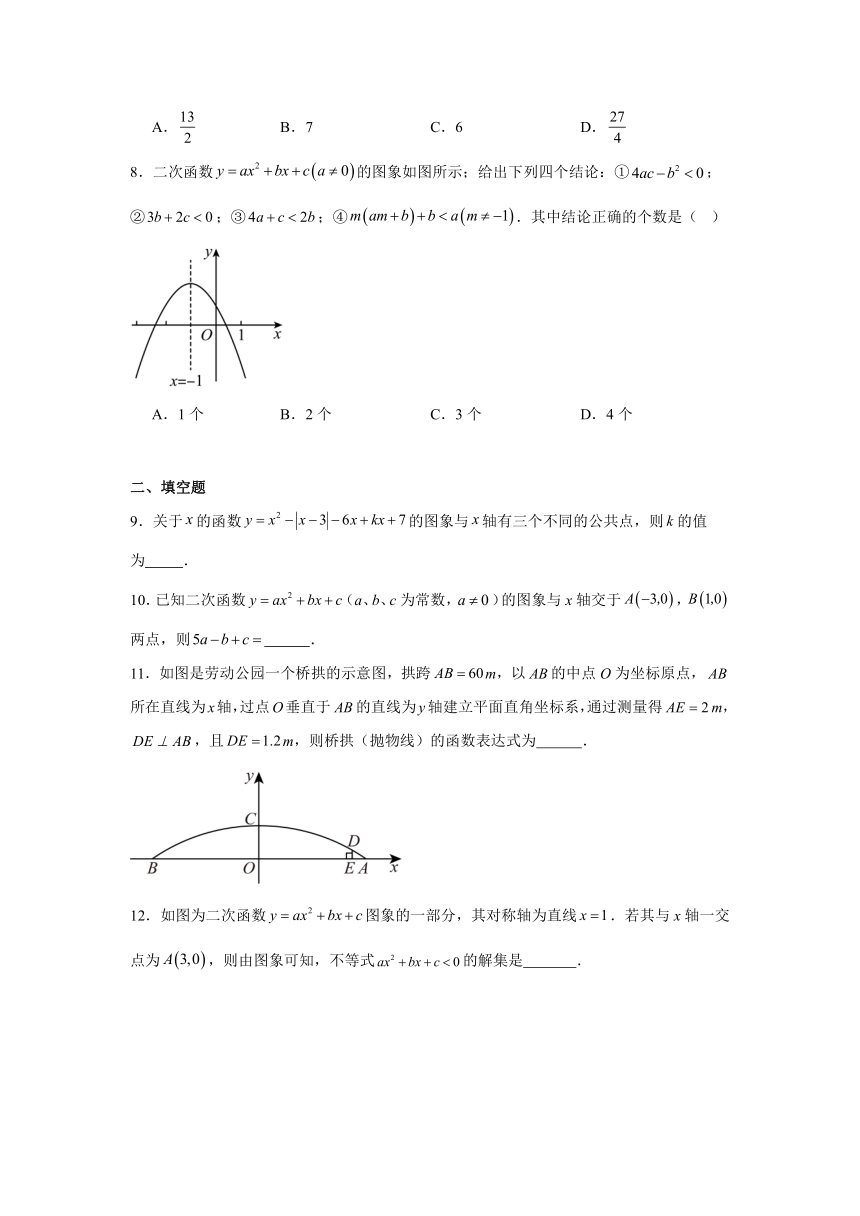
第二十二章 二次函数 同步练习
一、单选题
1.若点,在抛物线上,则它的对称轴是( )
A. B. C. D.
2.下列平移中,不能使二次函数经过点的是( )
A.向左平移2个单位 B.向右平移2个单位
C.向下平移3个单位 D.向上平移4个单位
3.某段公路上汽车紧急刹车后前行的距离s(单位:)关于行驶时间t(单位:)的函数解析式是,遇到刹车时,汽车从刹车后到停下来前进了( ).
A. B. C. D.
4.在同一平面直角坐标系中,函数和(m为常数,且)的图象可能是( )
A. B.
C. D.
5.在函数的图象上,当随的增大而减小时,的取值范围为( )
A. B. C. D.
6.在自变量x的取值范围内,对于自变量时,函数值,则称a是函数的一个不动点,若函数恰有一个不动点,则实数的值不可能是( )
A. B.0 C.1 D.4
7.已知与x轴、y轴正半轴分别相交于A、B两点,若M是抛物线在第一象限内的动点,则的最大值为( )
A. B.7 C.6 D.
8.二次函数的图象如图所示;给出下列四个结论:①;②;③;④.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.关于的函数的图象与轴有三个不同的公共点,则的值为 .
10.已知二次函数(a、b、c为常数,)的图象与x轴交于,两点,则 .
11.如图是劳动公园一个桥拱的示意图,拱跨m,以的中点O为坐标原点,所在直线为x轴,过点O垂直于的直线为y轴建立平面直角坐标系,通过测量得m,,且m,则桥拱(抛物线)的函数表达式为 .
12.如图为二次函数图象的一部分,其对称轴为直线.若其与x轴一交点为,则由图象可知,不等式的解集是 .
13.如图.在平面直角坐标系中,O为坐标原点,点A、B、M的坐标分别为、和,抛物线的顶点在线段(包括线段端点)上,与x轴交于C、D两点,点C在线段上(包括线段端点),设点D的横坐标为m,则m的最大值是 .
三、解答题
14.已知函数(m为常数).
(1)若该函数图象与y轴的交点在x轴上方,求m的取值范围:
(2)求证:不论m取何值,该函数图象与x轴总有两个公共点.
15.某商店销售一种成本为30元/千克的水产品,若按40元/千克销售,一个月可售出500千克,经调查知每涨价1元,月销售量就减少10千克,设售价为x(单位:元/千克),月销售利润为y(单位:元).
(1)请求出月销售利润y与售价x之间的函数解析式;
(2)商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元,售价应为多少元?
(3)当售价为多少元时会获得最大利润,并求出最大利润的值.
(4)月销售利润不低于8750元时,直接写出售价x 的取值范围.
16.如图,在平面直角坐标系中,点O为坐标原点,,抛物线与y轴交于点C,交x轴于A、B两点(A在B的左边),点E为抛物线第一象限上一动点.
(1)直接写出A,B两点坐标;
(2)连接,过点E作轴交于点F.
①当时,求点E的坐标;
②连接,,得到,求的面积的最大值.
17.如图,利用一面墙墙的长度为,用长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道宽的门,设的长为米.
(1)若两个鸡场的面积和为S,求S关于的关系式并写出的取值范围;
(2)两个鸡场面积和S有最大值吗?若有,最大值是多少?
18.如图,抛物线与轴交于,两点,与轴交于点,顶点为.其中,.
(1)直接写出该抛物线的解析式;
(2)如图1,连接,在第三象限内抛物线上找点,使,求点的坐标;
(3)如图2,为抛物线上任意一点,过做直线与抛物线有唯一交点(不与轴平行)交抛物线对称轴于点,为对称轴上一点,若始终满足,求点的坐标.
参考答案:
1.D
2.C
3.A
4.D
5.A
6.A
7.D
8.C
9.或
10.0
11.
12.
13.
14.(1)
(2)不论m为何值,该函数图象与x轴有两个不同的公共点
15.(1)
(2)售价应为70元
(3)当售价为60元时会获得最大利润,最大利润的值为9000元
(4)
16.(1),;
(2)①;②
17.(1),
(2)两个鸡场面积和有最大值,最大值是
18.(1)
(2)
(3)
一、单选题
1.若点,在抛物线上,则它的对称轴是( )
A. B. C. D.
2.下列平移中,不能使二次函数经过点的是( )
A.向左平移2个单位 B.向右平移2个单位
C.向下平移3个单位 D.向上平移4个单位
3.某段公路上汽车紧急刹车后前行的距离s(单位:)关于行驶时间t(单位:)的函数解析式是,遇到刹车时,汽车从刹车后到停下来前进了( ).
A. B. C. D.
4.在同一平面直角坐标系中,函数和(m为常数,且)的图象可能是( )
A. B.
C. D.
5.在函数的图象上,当随的增大而减小时,的取值范围为( )
A. B. C. D.
6.在自变量x的取值范围内,对于自变量时,函数值,则称a是函数的一个不动点,若函数恰有一个不动点,则实数的值不可能是( )
A. B.0 C.1 D.4
7.已知与x轴、y轴正半轴分别相交于A、B两点,若M是抛物线在第一象限内的动点,则的最大值为( )
A. B.7 C.6 D.
8.二次函数的图象如图所示;给出下列四个结论:①;②;③;④.其中结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.关于的函数的图象与轴有三个不同的公共点,则的值为 .
10.已知二次函数(a、b、c为常数,)的图象与x轴交于,两点,则 .
11.如图是劳动公园一个桥拱的示意图,拱跨m,以的中点O为坐标原点,所在直线为x轴,过点O垂直于的直线为y轴建立平面直角坐标系,通过测量得m,,且m,则桥拱(抛物线)的函数表达式为 .
12.如图为二次函数图象的一部分,其对称轴为直线.若其与x轴一交点为,则由图象可知,不等式的解集是 .
13.如图.在平面直角坐标系中,O为坐标原点,点A、B、M的坐标分别为、和,抛物线的顶点在线段(包括线段端点)上,与x轴交于C、D两点,点C在线段上(包括线段端点),设点D的横坐标为m,则m的最大值是 .
三、解答题
14.已知函数(m为常数).
(1)若该函数图象与y轴的交点在x轴上方,求m的取值范围:
(2)求证:不论m取何值,该函数图象与x轴总有两个公共点.
15.某商店销售一种成本为30元/千克的水产品,若按40元/千克销售,一个月可售出500千克,经调查知每涨价1元,月销售量就减少10千克,设售价为x(单位:元/千克),月销售利润为y(单位:元).
(1)请求出月销售利润y与售价x之间的函数解析式;
(2)商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元,售价应为多少元?
(3)当售价为多少元时会获得最大利润,并求出最大利润的值.
(4)月销售利润不低于8750元时,直接写出售价x 的取值范围.
16.如图,在平面直角坐标系中,点O为坐标原点,,抛物线与y轴交于点C,交x轴于A、B两点(A在B的左边),点E为抛物线第一象限上一动点.
(1)直接写出A,B两点坐标;
(2)连接,过点E作轴交于点F.
①当时,求点E的坐标;
②连接,,得到,求的面积的最大值.
17.如图,利用一面墙墙的长度为,用长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道宽的门,设的长为米.
(1)若两个鸡场的面积和为S,求S关于的关系式并写出的取值范围;
(2)两个鸡场面积和S有最大值吗?若有,最大值是多少?
18.如图,抛物线与轴交于,两点,与轴交于点,顶点为.其中,.
(1)直接写出该抛物线的解析式;
(2)如图1,连接,在第三象限内抛物线上找点,使,求点的坐标;
(3)如图2,为抛物线上任意一点,过做直线与抛物线有唯一交点(不与轴平行)交抛物线对称轴于点,为对称轴上一点,若始终满足,求点的坐标.
参考答案:
1.D
2.C
3.A
4.D
5.A
6.A
7.D
8.C
9.或
10.0
11.
12.
13.
14.(1)
(2)不论m为何值,该函数图象与x轴有两个不同的公共点
15.(1)
(2)售价应为70元
(3)当售价为60元时会获得最大利润,最大利润的值为9000元
(4)
16.(1),;
(2)①;②
17.(1),
(2)两个鸡场面积和有最大值,最大值是
18.(1)
(2)
(3)
同课章节目录
