期中试题重组练习卷(含详解)2024-2025学年苏科版数学九年级上册
文档属性
| 名称 | 期中试题重组练习卷(含详解)2024-2025学年苏科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 483.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 16:12:43 | ||
图片预览




文档简介
期中试题重组练习卷-2024-2025学年数学九年级上册苏科版
一.选择题(共8小题)
1.(2024春 徐汇区期中)下列方程,有实数解的是( )
A. B.
C. D.
2.(2024秋 沙坪坝区校级期中)已知实数m,n(m≠n)满足2m2﹣3m﹣1=0,2n2﹣3n﹣1=0,则的值为( )
A. B. C. D.
3.(2023秋 香洲区校级期中)用配方法解一元二次方程x2﹣6x+8=0,配方后得到的方程是( )
A.(x+6)2=17 B.(x﹣6)2=17 C.(x+3)2=1 D.(x﹣3)2=1
4.(2024秋 德惠市期中)为了促进教育事业的发展,某县加强了对教育经费的投入,2022年共计投入3.4亿元,预计2024年投入4.9亿元,设教育经费的年平均增长率为x,下面所列方程正确的是( )
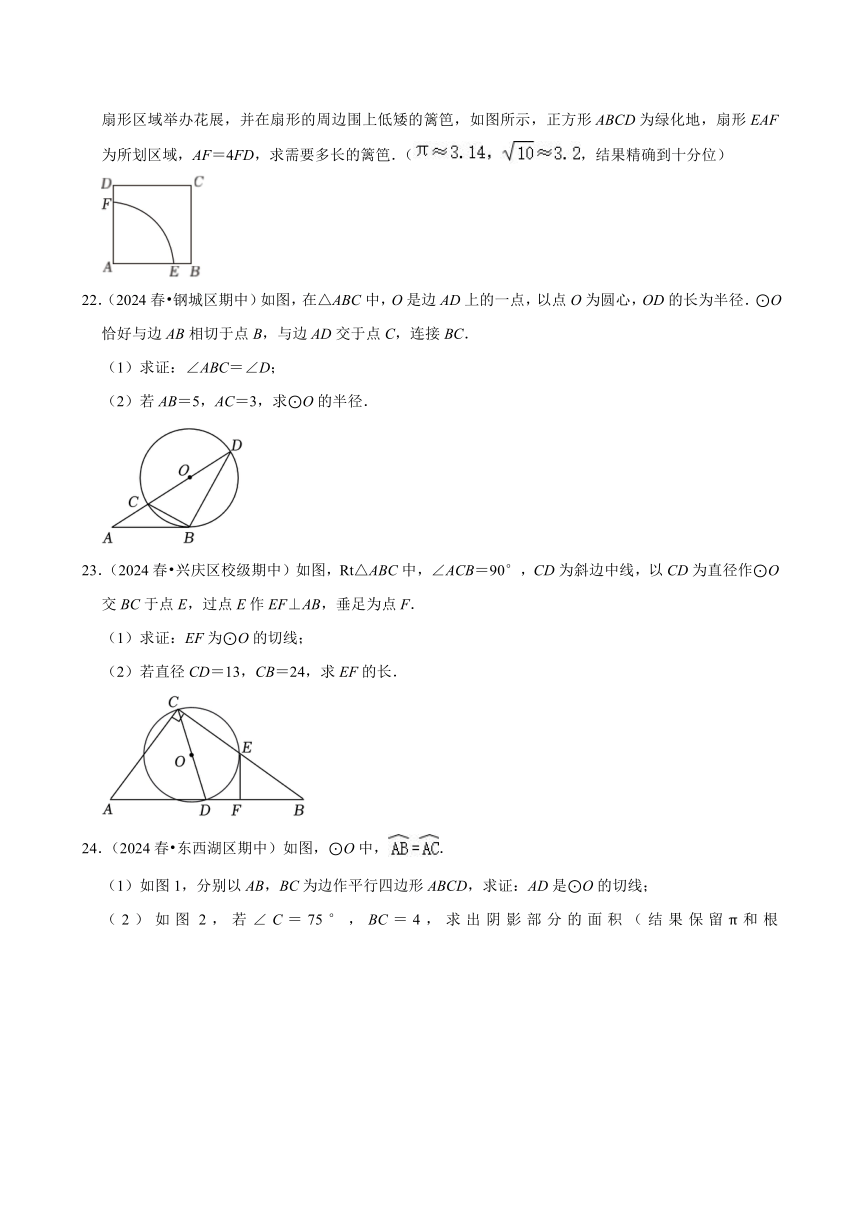
A.3.4(1+x)2=4.9
B.3.4x2=5
C.3.4(1+x%)2=4.9
D.3.4(1+x)2+3.4(1+x)=4.9
5.(2024春 馆陶县期中)嘉嘉的一面圆形镜子摔碎了,想配一面与原来大小相同的镜子,她把三角板的30°顶点A放在圆上,将两边与圆的交点分别记为点B,C,如图所示,经测量弦BC的长为6cm,则该镜子的直径为( )
A.6cm B.9cm C.12cm D.15cm
6.(2024春 馆陶县期中)如图是某同学自制的一个乒乓球拍,正面是半径为8cm的⊙O,劣弧的长为4πcm,阴影部分需要粘贴胶度,则胶皮的面积为( )
A.(32+48π)cm2 B.(16π﹣32)cm2
C.64πcm2 D.(48π﹣32)cm2
7.(2024春 上城区校级期中)如图,已知AB为⊙O的直径,弦CD与AB交于点E,连结OD、BC,设∠AOD=α,∠B=β,则∠AED=( )
A.α+β B. C.180﹣α﹣β D.
8.(2024春 秀英区校级期中)如图,⊙O的直径AB是4,弦CE交AB于点D.当D为AO的中点时,记CE的最小值为a,当∠CDB=60°时,记CE的最小值为b,则a﹣b的值为( )
A. B. C. D.
二.填空题(共8小题)
9.(2024春 沙坡头区校级期中)已知关于x的一元二次方程2x2﹣4x﹣1+k=0有两个相等的实数根,则k的值是 .
10.(2024春 博望区校级期中)一元二次方程2x2﹣7x﹣4=0的两根为x1,x2,则= .
11.(2024秋 东莞市期中)泉泉自制了一款等腰三角形晾衣架,设计的平面图如图所示,已知该晾衣架的底边长为30cm,另外两边长是方程x2﹣bx+400=0的两个根,则该晾衣架三角形部分的周长为 cm.
12.(2024春 双流区校级期中)如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,且|x1﹣x2|=1,那么称这样的方程为“邻近根方程”,例如,一元二次方程x2+x=0的两个根是x1=0,x2=﹣1,|0﹣(﹣1)|=1,则方程x2+x=0是“邻近根方程”.若关于x的方程ax2+bx+2=0(a,b是常数,且a>0)是“邻近根方程”,令t=b2﹣4a2,则t的最大值为 .
13.(2023秋 江都区校级期中)若圆锥的底面圆半径为3,母线长为5,则该圆锥的侧面积是 .(结果保留π)
14.(2023秋 西乡塘区校级期中)如图,四边形ABCD是⊙O的内接四边形,∠A=50°,则∠C的度数是 .
15.(2023秋 赛罕区校级期中)如图,点A,B,C,D都在直径为的⊙O上,若OA⊥BC,∠CDA=27°,则阴影部分扇形的面积是 .
16.(2024秋 九台区期中)日常生活中常见的装饰盘由圆盘和支架组成(如图1),它可以看作如图2所示的几何图形.已知AC=BD=5cm,AC⊥CD,垂足为点C,BD⊥CD,垂足为点D,CD=16cm,⊙O的半径r=10cm,则圆盘离桌面CD最近的距离是 .
三.解答题(共8小题)
17.(2024春 张店区校级期中)解方程:
(1)x2﹣14x+21=0.
(2)3x2﹣6x=4(x﹣2).
18.(2024秋 东莞市期中)若关于x的一元二次方程x2﹣2(m+1)x+m2+5=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2恰好是对角线长为6的矩形的相邻两边的边长,求这个矩形的周长.
19.(2024春 睢宁县期中)问题:当a≠b时,判断a2+b2与2ab的大小关系.
(1)①小明说,当a>b>0时,可以构造如图所示的长方形ABCD,它是由1个正方形ABFE和1个长方形EFCD拼成.请你完成下面的推理过程.
②当b>a>0时,请你类比小明的思路,完成构图和推理.
(2)小红说,可以用“作差法”比较a2+b2与2ab的大小.请你尝试根据她的思路解决问题.
20.(2022秋 麻阳县期中)云南某地一村民,2021年承包种植橙子树200亩,由于第一年收成不错,该村民每年都增加种植面积,到2023年共种植288亩.假设每年的增长率相同.
(1)求该村民这两年种植橙子亩数的平均增长率.
(2)某水果批发店销售该种橙子,市场调查发现,当橙子售价为18元/千克时,每天能售出120千克,售价每降低1元,每天可多售出15千克,为了减少库存,该店决定降价促销,已知该橙子的平均成本价为8元/千克,若使销售该种橙子每天获利840元,则售价应降低多少元?
21.(2024春 静安区校级期中)公园里有一块面积为10平方米的正方形绿化地,现在这块地上划出一个扇形区域举办花展,并在扇形的周边围上低矮的篱笆,如图所示,正方形ABCD为绿化地,扇形EAF为所划区域,AF=4FD,求需要多长的篱笆.(,结果精确到十分位)
22.(2024春 钢城区期中)如图,在△ABC中,O是边AD上的一点,以点O为圆心,OD的长为半径.⊙O恰好与边AB相切于点B,与边AD交于点C,连接BC.
(1)求证:∠ABC=∠D;
(2)若AB=5,AC=3,求⊙O的半径.
23.(2024春 兴庆区校级期中)如图,Rt△ABC中,∠ACB=90°,CD为斜边中线,以CD为直径作⊙O交BC于点E,过点E作EF⊥AB,垂足为点F.
(1)求证:EF为⊙O的切线;
(2)若直径CD=13,CB=24,求EF的长.
24.(2024春 东西湖区期中)如图,⊙O中,.
(1)如图1,分别以AB,BC为边作平行四边形ABCD,求证:AD是⊙O的切线;
(2)如图2,若∠C=75°,BC=4,求出阴影部分的面积(结果保留π和根号).
期中试题重组练习卷-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2024春 徐汇区期中)下列方程,有实数解的是( )
A. B.
C. D.
【解答】解:由得:,
∵,
∴原方程无实数解,故A错误;
由得:,
即:x2﹣9x+4=0,
Δ=(﹣9)2﹣4×4=65>0;
∴原方程有实数解,故B正确;
由得:x2﹣3x+3=0,
Δ=(﹣3)2﹣4×1×3=﹣3<0,
∴原方程无实数解,故C错误;
∵,又,
∴x=5且x=﹣1(矛盾),
∴原方程无实数解,故D错误;
故选:B.
2.(2024秋 沙坪坝区校级期中)已知实数m,n(m≠n)满足2m2﹣3m﹣1=0,2n2﹣3n﹣1=0,则的值为( )
A. B. C. D.
【解答】解:∵实数m,n(m≠n)满足2m2﹣3m﹣1=0,2n2﹣3n﹣1=0,
∴m,n是方程2x2﹣3x﹣1=0的两根,
∴m+n=,mn=﹣,
∴+====﹣.
故选:B.
3.(2023秋 香洲区校级期中)用配方法解一元二次方程x2﹣6x+8=0,配方后得到的方程是( )
A.(x+6)2=17 B.(x﹣6)2=17 C.(x+3)2=1 D.(x﹣3)2=1
【解答】解:x2﹣6x+8=0,
x2﹣6x=﹣8,
x2﹣6x+9=﹣8+9,
(x﹣3)2=1,
故选:D.
4.(2024秋 德惠市期中)为了促进教育事业的发展,某县加强了对教育经费的投入,2022年共计投入3.4亿元,预计2024年投入4.9亿元,设教育经费的年平均增长率为x,下面所列方程正确的是( )
A.3.4(1+x)2=4.9
B.3.4x2=5
C.3.4(1+x%)2=4.9
D.3.4(1+x)2+3.4(1+x)=4.9
【解答】解:由题意可得,
3.4(1+x)2=4.9,
故选:A.
5.(2024春 馆陶县期中)嘉嘉的一面圆形镜子摔碎了,想配一面与原来大小相同的镜子,她把三角板的30°顶点A放在圆上,将两边与圆的交点分别记为点B,C,如图所示,经测量弦BC的长为6cm,则该镜子的直径为( )
A.6cm B.9cm C.12cm D.15cm
【解答】解:如图所示,作AB、BC的垂直平分线,交点即为圆心O,连接OC,OB,
∵∠A=30°,
∴∠COB=2∠A=60°,
又∵OC=OB,
∴△OCB是等边三角形,
∴OB=6cm,
∴该镜子的直径为12cm,
故选:C.
6.(2024春 馆陶县期中)如图是某同学自制的一个乒乓球拍,正面是半径为8cm的⊙O,劣弧的长为4πcm,阴影部分需要粘贴胶度,则胶皮的面积为( )
A.(32+48π)cm2 B.(16π﹣32)cm2
C.64πcm2 D.(48π﹣32)cm2
【解答】解:连接OA、OB.
设⊙O的半径为R,则R=8cm.
设∠AOB=n°,根据题意,得劣弧=×2πR,
解得n=90°,
∴S扇形AOB=×πR2=16π(cm2),SRt△AOB=OA OB=R2=32(cm2),
∴S空白弓形=S扇形AOB﹣SRt△AOB=(16π﹣32)(cm2),
∴S阴影=S⊙O﹣S空白弓形=πR2﹣(16π﹣32)=(32+48π)(cm2).
故选:A.
7.(2024春 上城区校级期中)如图,已知AB为⊙O的直径,弦CD与AB交于点E,连结OD、BC,设∠AOD=α,∠B=β,则∠AED=( )
A.α+β B. C.180﹣α﹣β D.
【解答】解:∵∠AOD=α,
∴∠BOD=180°﹣∠AOD=180°﹣α,
由圆周角定理得,∠BCD=,
在△BCE中,∠BEC=180°﹣∠BCD﹣∠B=180°﹣=,
∴∠AED=∠BEC=,
故选:B.
8.(2024春 秀英区校级期中)如图,⊙O的直径AB是4,弦CE交AB于点D.当D为AO的中点时,记CE的最小值为a,当∠CDB=60°时,记CE的最小值为b,则a﹣b的值为( )
A. B. C. D.
【解答】解:当D为AO的中点时,CE的最小值为a,此时CE⊥AB,如图1,连接OC,
∵D为OA的中点,OA、OC为⊙O的半径,⊙O的直径AB为4,
∴CD=CE,OA=OC=AB=2,
∴OD==AO=1,
根据勾股定理可得:CD==,
∴此时CE的最小值a=2CD=;
当∠CDB=60°时,此时点D、E与点A重合,即CE即为CA,如图2,连接OC,
∵∠CDB=60°,OA=OC=2,
∴△OAC是等边三角形,
∴AC=OA=2.
∴此时CE的最小值b=2;
∴a﹣b=﹣2,
故选C.
二.填空题(共8小题)
9.(2024春 沙坡头区校级期中)已知关于x的一元二次方程2x2﹣4x﹣1+k=0有两个相等的实数根,则k的值是 3 .
【解答】解:∵一元二次方程2x2﹣4x﹣1+k=0有两个相等的实数根,
∴Δ=(﹣4)2﹣4×2×(k﹣1)=0,
解得:k=3;
故答案为:3.
10.(2024春 博望区校级期中)一元二次方程2x2﹣7x﹣4=0的两根为x1,x2,则= .
【解答】解:∵一元二次方程2x2﹣7x﹣4=0的两根为x1,x2,
∴,
∴,
故答案为:.
11.(2024秋 东莞市期中)泉泉自制了一款等腰三角形晾衣架,设计的平面图如图所示,已知该晾衣架的底边长为30cm,另外两边长是方程x2﹣bx+400=0的两个根,则该晾衣架三角形部分的周长为 70 cm.
【解答】解:令等腰三角形的腰长为a cm,
因为等腰三角形的两条腰长是方程x2﹣bx+400=0的两个根,
所以a2=400,
则a=20(舍负),
即晾衣架的两条腰长都为20cm.
又因为该晾衣架的底边长为30cm,
所以该晾衣架三角形部分的周长为70cm.
故答案为:70.
12.(2024春 双流区校级期中)如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,且|x1﹣x2|=1,那么称这样的方程为“邻近根方程”,例如,一元二次方程x2+x=0的两个根是x1=0,x2=﹣1,|0﹣(﹣1)|=1,则方程x2+x=0是“邻近根方程”.若关于x的方程ax2+bx+2=0(a,b是常数,且a>0)是“邻近根方程”,令t=b2﹣4a2,则t的最大值为 .
【解答】解:设方程ax2+bx+2=0的两个根为x1,x2,
∴,
∵关于x的方程ax2+bx+2=0是“邻近根方程”,
∴|x1﹣x2|=1,
∴,
∴,
∴,
整理得:b2=a2+8a,
∴t=b2﹣4a2
=a2+8a﹣4a2
=﹣3a2+8a
=,
∵﹣3<0,
∴,
故答案为:.
13.(2023秋 江都区校级期中)若圆锥的底面圆半径为3,母线长为5,则该圆锥的侧面积是 15π .(结果保留π)
【解答】解:根据圆锥的侧面积公式:πrl=π×3×5=15π,
故答案为:15π.
14.(2023秋 西乡塘区校级期中)如图,四边形ABCD是⊙O的内接四边形,∠A=50°,则∠C的度数是 130° .
【解答】解:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,
∵∠A=50°,
∴∠C=130°,
故答案为:130°.
15.(2023秋 赛罕区校级期中)如图,点A,B,C,D都在直径为的⊙O上,若OA⊥BC,∠CDA=27°,则阴影部分扇形的面积是 .
【解答】解:∵OA⊥BC,
∴,
∴∠AOB=2∠CDA=54°,
∴.
故答案为:.
16.(2024秋 九台区期中)日常生活中常见的装饰盘由圆盘和支架组成(如图1),它可以看作如图2所示的几何图形.已知AC=BD=5cm,AC⊥CD,垂足为点C,BD⊥CD,垂足为点D,CD=16cm,⊙O的半径r=10cm,则圆盘离桌面CD最近的距离是 1cm .
【解答】解:如图2,连接AB,OA,过点O作OG⊥CD于点G,交AB于点E,交⊙O于点F.
∵AC⊥CD,BD⊥CD,
∴AC∥BD,
∵AC=BD,
∴四边形ACDB是平行四边形,
∵∠ACD=90°,
∴四边形ACDB是矩形,
∴AB∥CD,AB=CD=16cm,
∵OG⊥CD,
∴OG⊥AB,
∴AE=EB=8cm,
∴OE===6(cm),
∴EF=OF﹣OE=10﹣6=4(cm),
∵EG=AC=BD=5cm,
∴FG=EG﹣EF=5﹣4=1(cm),
∴圆盘离桌面CD最近的距离是1cm,
故答案为:1cm.
三.解答题(共8小题)
17.(2024春 张店区校级期中)解方程:
(1)x2﹣14x+21=0.
(2)3x2﹣6x=4(x﹣2).
【解答】解:(1)∵x2﹣14x+21=0,
∴x2﹣14x=﹣21,
∴x2﹣14x+49=﹣21+49,
即(x﹣7)2=28,
∴,
∴,;
(2)移项提取公因式得,3x(x﹣2)﹣4(x﹣2)=0,
因式分解得,(x﹣2)(3x﹣4)=0,
∴x﹣2=0或3x﹣4=0,
∴x1=2,.
18.(2024秋 东莞市期中)若关于x的一元二次方程x2﹣2(m+1)x+m2+5=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2恰好是对角线长为6的矩形的相邻两边的边长,求这个矩形的周长.
【解答】解:(1)根据题意,得:Δ=[﹣2(m+1)]2﹣4(m2+5)=8m﹣16≥0,
解得:m≥2;
(2)由根与系数的关系可知x1+x2=2(m+1),,
∵x1,x2恰好是对角线长为6的矩形的相邻两边的边长,
∴,
整理,得m2+4m﹣21=0,
∴m1=3,m2=﹣7,
又∵m≥2,且x1+x2=2(m+1)>0,
∴m=3,
∴这个矩形的周长为:
2(x1+x2)=4(m+1)=16.
19.(2024春 睢宁县期中)问题:当a≠b时,判断a2+b2与2ab的大小关系.
(1)①小明说,当a>b>0时,可以构造如图所示的长方形ABCD,它是由1个正方形ABFE和1个长方形EFCD拼成.请你完成下面的推理过程.
②当b>a>0时,请你类比小明的思路,完成构图和推理.
(2)小红说,可以用“作差法”比较a2+b2与2ab的大小.请你尝试根据她的思路解决问题.
【解答】解:(1)①推理如下:
∵S长方形ABCD=a(a﹣b)=a2﹣ab,S长方形EFCD=b(a﹣b)=ab﹣b2,
由图形可得S长方形ABCD>S长方形EFCD,
∴a2﹣ab>ab﹣b2,
∴a2+b2>2ab;
②构造的图形如下:
推理如下:
∵S长方形ABCD=b(b﹣a)=b2﹣ab,S长方形EFCD=a(b﹣a)=ab﹣a2,
由图形可得S长方形ABCD>S长方形EFCD,
∴b2﹣ab>ab﹣a2,
∴a2+b2>2ab;
(2)作差可得,a2+b2﹣2ab=(a﹣b)2,
∵a≠b,
∴(a﹣b)2>0,
∴a2+b2﹣2ab>0,
∴a2+b2>2ab.
20.(2022秋 麻阳县期中)云南某地一村民,2021年承包种植橙子树200亩,由于第一年收成不错,该村民每年都增加种植面积,到2023年共种植288亩.假设每年的增长率相同.
(1)求该村民这两年种植橙子亩数的平均增长率.
(2)某水果批发店销售该种橙子,市场调查发现,当橙子售价为18元/千克时,每天能售出120千克,售价每降低1元,每天可多售出15千克,为了减少库存,该店决定降价促销,已知该橙子的平均成本价为8元/千克,若使销售该种橙子每天获利840元,则售价应降低多少元?
【解答】解:(1)设该村民这两年种植橙子亩数的平均增长率为x,
根据题意得:200(1+x)2=288,
解得:x1=0.2=20%,x2=﹣2.2(不符合题意,舍去).
答:该村民这两年种植橙子亩数的平均增长率为20%;
(2)设售价应降价y元,则每千克的销售利润为(18﹣y﹣8)元,每天能售出(120+15y)千克,
根据题意得:(18﹣y﹣8)(120+15y)=840,
整理得:y2﹣2y﹣24=0,
解得:y1=6,y2=﹣4(不符合题意,舍去).
答:售价应降低6元.
21.(2024春 静安区校级期中)公园里有一块面积为10平方米的正方形绿化地,现在这块地上划出一个扇形区域举办花展,并在扇形的周边围上低矮的篱笆,如图所示,正方形ABCD为绿化地,扇形EAF为所划区域,AF=4FD,求需要多长的篱笆.(,结果精确到十分位)
【解答】解:∵公园里有一块面积为10平方米的正方形ABCD绿化地,
∴米,
∵AF=4FD,AD+DF=AD,
∴米,
∵扇形EAF为所划区域,
∴米,扇形的周长=(米),
∴需要的篱笆长度=(米),
∴需要9.1米的篱笆.
22.(2024春 钢城区期中)如图,在△ABC中,O是边AD上的一点,以点O为圆心,OD的长为半径.⊙O恰好与边AB相切于点B,与边AD交于点C,连接BC.
(1)求证:∠ABC=∠D;
(2)若AB=5,AC=3,求⊙O的半径.
【解答】(1)证明:连接OB,
∵AB与⊙O相切于B,
∴OB⊥AB,
∴∠ABC+∠CBO=90°,
∵CD是圆的直径,
∴∠CBD=90°,
∴∠D+∠OCB=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠ABC=∠D;
(2)解:∵∠D=∠ABC,
∵∠CAB=∠BAD,
∴△ABC∽△ADB,
∴AB:AD=AC:AB,
∵AB=5,AC=3,
∴5:AD=3:5,
∴AD=,
∴CD=AD﹣AC=,
∴⊙O的半径是CD=.
23.(2024春 兴庆区校级期中)如图,Rt△ABC中,∠ACB=90°,CD为斜边中线,以CD为直径作⊙O交BC于点E,过点E作EF⊥AB,垂足为点F.
(1)求证:EF为⊙O的切线;
(2)若直径CD=13,CB=24,求EF的长.
【解答】(1)证明:连接OE,如图所示:
∵以CD为直径作⊙O交BC于点E,
∴OC=OE,
∴∠OCE=∠OEC,
∵在Rt△ABC中,∠ACB=90°,CD为斜边中线,
∴CD=AD=BD,
∴∠OCE=∠B,
∴∠OEC∠B,
∴OE∥AB,
∵EF⊥AB,
∴OE⊥EF,
又∵OE为⊙O半径,
EF为⊙O的切线;
(2)解:∵CD=13,CB=24,
∴AD=BD=CD=13,
∴AB=26,
在Rt△ABC中,∠ACB=90°,
由勾股定理得:AC==10,
∵AD为⊙O直径,
∴OC=OD,
又∵OE∥AB,
∴OE为△CDB的中位线,
∴CE=BE=CB=12,
∵EF⊥AB,∠ACB=90°,
∴∠EFB=∠ACB=90°,
又∵∠B=∠B,
∴△BEF∽△BAC,
∴EF:AC=BE:AB,
即EF:10=12:26,
∴EF=.
24.(2024春 东西湖区期中)如图,⊙O中,.
(1)如图1,分别以AB,BC为边作平行四边形ABCD,求证:AD是⊙O的切线;
(2)如图2,若∠C=75°,BC=4,求出阴影部分的面积(结果保留π和根号).
【解答】(1)证明:连接AO,并延长交BC于点E,如图,
∵,
∴AE⊥BC,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴OA⊥AD.
∵OA为⊙O的半径,
∴AD是⊙O的切线;
(2)解:连接OB,OC,连接AO,并延长交BC于点D,如图,
∵,
∴AB=AC,AD⊥BC,
∴∠ABC=∠ACB=75°,
∴∠BAC=30°,
∴∠BOC=2∠BAC=60°.
∵OB=OC,
∴△OBC为等边三角形,
∴OB=OC=BC=4,
∴OA=OB=4.
∵OD⊥BC,
∴BD=DC=2,
∴OD==2.
∴AD=OA+OD=4+2.
∴BC AD=4×(4+2)=8+4.
∵S弓形BEC=S扇形OBC﹣S△OBC==π﹣4,
∴S阴影=S弓形BEC+S△ABC=+8.
一.选择题(共8小题)
1.(2024春 徐汇区期中)下列方程,有实数解的是( )
A. B.
C. D.
2.(2024秋 沙坪坝区校级期中)已知实数m,n(m≠n)满足2m2﹣3m﹣1=0,2n2﹣3n﹣1=0,则的值为( )
A. B. C. D.
3.(2023秋 香洲区校级期中)用配方法解一元二次方程x2﹣6x+8=0,配方后得到的方程是( )
A.(x+6)2=17 B.(x﹣6)2=17 C.(x+3)2=1 D.(x﹣3)2=1
4.(2024秋 德惠市期中)为了促进教育事业的发展,某县加强了对教育经费的投入,2022年共计投入3.4亿元,预计2024年投入4.9亿元,设教育经费的年平均增长率为x,下面所列方程正确的是( )
A.3.4(1+x)2=4.9
B.3.4x2=5
C.3.4(1+x%)2=4.9
D.3.4(1+x)2+3.4(1+x)=4.9
5.(2024春 馆陶县期中)嘉嘉的一面圆形镜子摔碎了,想配一面与原来大小相同的镜子,她把三角板的30°顶点A放在圆上,将两边与圆的交点分别记为点B,C,如图所示,经测量弦BC的长为6cm,则该镜子的直径为( )
A.6cm B.9cm C.12cm D.15cm
6.(2024春 馆陶县期中)如图是某同学自制的一个乒乓球拍,正面是半径为8cm的⊙O,劣弧的长为4πcm,阴影部分需要粘贴胶度,则胶皮的面积为( )
A.(32+48π)cm2 B.(16π﹣32)cm2
C.64πcm2 D.(48π﹣32)cm2
7.(2024春 上城区校级期中)如图,已知AB为⊙O的直径,弦CD与AB交于点E,连结OD、BC,设∠AOD=α,∠B=β,则∠AED=( )
A.α+β B. C.180﹣α﹣β D.
8.(2024春 秀英区校级期中)如图,⊙O的直径AB是4,弦CE交AB于点D.当D为AO的中点时,记CE的最小值为a,当∠CDB=60°时,记CE的最小值为b,则a﹣b的值为( )
A. B. C. D.
二.填空题(共8小题)
9.(2024春 沙坡头区校级期中)已知关于x的一元二次方程2x2﹣4x﹣1+k=0有两个相等的实数根,则k的值是 .
10.(2024春 博望区校级期中)一元二次方程2x2﹣7x﹣4=0的两根为x1,x2,则= .
11.(2024秋 东莞市期中)泉泉自制了一款等腰三角形晾衣架,设计的平面图如图所示,已知该晾衣架的底边长为30cm,另外两边长是方程x2﹣bx+400=0的两个根,则该晾衣架三角形部分的周长为 cm.
12.(2024春 双流区校级期中)如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,且|x1﹣x2|=1,那么称这样的方程为“邻近根方程”,例如,一元二次方程x2+x=0的两个根是x1=0,x2=﹣1,|0﹣(﹣1)|=1,则方程x2+x=0是“邻近根方程”.若关于x的方程ax2+bx+2=0(a,b是常数,且a>0)是“邻近根方程”,令t=b2﹣4a2,则t的最大值为 .
13.(2023秋 江都区校级期中)若圆锥的底面圆半径为3,母线长为5,则该圆锥的侧面积是 .(结果保留π)
14.(2023秋 西乡塘区校级期中)如图,四边形ABCD是⊙O的内接四边形,∠A=50°,则∠C的度数是 .
15.(2023秋 赛罕区校级期中)如图,点A,B,C,D都在直径为的⊙O上,若OA⊥BC,∠CDA=27°,则阴影部分扇形的面积是 .
16.(2024秋 九台区期中)日常生活中常见的装饰盘由圆盘和支架组成(如图1),它可以看作如图2所示的几何图形.已知AC=BD=5cm,AC⊥CD,垂足为点C,BD⊥CD,垂足为点D,CD=16cm,⊙O的半径r=10cm,则圆盘离桌面CD最近的距离是 .
三.解答题(共8小题)
17.(2024春 张店区校级期中)解方程:
(1)x2﹣14x+21=0.
(2)3x2﹣6x=4(x﹣2).
18.(2024秋 东莞市期中)若关于x的一元二次方程x2﹣2(m+1)x+m2+5=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2恰好是对角线长为6的矩形的相邻两边的边长,求这个矩形的周长.
19.(2024春 睢宁县期中)问题:当a≠b时,判断a2+b2与2ab的大小关系.
(1)①小明说,当a>b>0时,可以构造如图所示的长方形ABCD,它是由1个正方形ABFE和1个长方形EFCD拼成.请你完成下面的推理过程.
②当b>a>0时,请你类比小明的思路,完成构图和推理.
(2)小红说,可以用“作差法”比较a2+b2与2ab的大小.请你尝试根据她的思路解决问题.
20.(2022秋 麻阳县期中)云南某地一村民,2021年承包种植橙子树200亩,由于第一年收成不错,该村民每年都增加种植面积,到2023年共种植288亩.假设每年的增长率相同.
(1)求该村民这两年种植橙子亩数的平均增长率.
(2)某水果批发店销售该种橙子,市场调查发现,当橙子售价为18元/千克时,每天能售出120千克,售价每降低1元,每天可多售出15千克,为了减少库存,该店决定降价促销,已知该橙子的平均成本价为8元/千克,若使销售该种橙子每天获利840元,则售价应降低多少元?
21.(2024春 静安区校级期中)公园里有一块面积为10平方米的正方形绿化地,现在这块地上划出一个扇形区域举办花展,并在扇形的周边围上低矮的篱笆,如图所示,正方形ABCD为绿化地,扇形EAF为所划区域,AF=4FD,求需要多长的篱笆.(,结果精确到十分位)
22.(2024春 钢城区期中)如图,在△ABC中,O是边AD上的一点,以点O为圆心,OD的长为半径.⊙O恰好与边AB相切于点B,与边AD交于点C,连接BC.
(1)求证:∠ABC=∠D;
(2)若AB=5,AC=3,求⊙O的半径.
23.(2024春 兴庆区校级期中)如图,Rt△ABC中,∠ACB=90°,CD为斜边中线,以CD为直径作⊙O交BC于点E,过点E作EF⊥AB,垂足为点F.
(1)求证:EF为⊙O的切线;
(2)若直径CD=13,CB=24,求EF的长.
24.(2024春 东西湖区期中)如图,⊙O中,.
(1)如图1,分别以AB,BC为边作平行四边形ABCD,求证:AD是⊙O的切线;
(2)如图2,若∠C=75°,BC=4,求出阴影部分的面积(结果保留π和根号).
期中试题重组练习卷-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2024春 徐汇区期中)下列方程,有实数解的是( )
A. B.
C. D.
【解答】解:由得:,
∵,
∴原方程无实数解,故A错误;
由得:,
即:x2﹣9x+4=0,
Δ=(﹣9)2﹣4×4=65>0;
∴原方程有实数解,故B正确;
由得:x2﹣3x+3=0,
Δ=(﹣3)2﹣4×1×3=﹣3<0,
∴原方程无实数解,故C错误;
∵,又,
∴x=5且x=﹣1(矛盾),
∴原方程无实数解,故D错误;
故选:B.
2.(2024秋 沙坪坝区校级期中)已知实数m,n(m≠n)满足2m2﹣3m﹣1=0,2n2﹣3n﹣1=0,则的值为( )
A. B. C. D.
【解答】解:∵实数m,n(m≠n)满足2m2﹣3m﹣1=0,2n2﹣3n﹣1=0,
∴m,n是方程2x2﹣3x﹣1=0的两根,
∴m+n=,mn=﹣,
∴+====﹣.
故选:B.
3.(2023秋 香洲区校级期中)用配方法解一元二次方程x2﹣6x+8=0,配方后得到的方程是( )
A.(x+6)2=17 B.(x﹣6)2=17 C.(x+3)2=1 D.(x﹣3)2=1
【解答】解:x2﹣6x+8=0,
x2﹣6x=﹣8,
x2﹣6x+9=﹣8+9,
(x﹣3)2=1,
故选:D.
4.(2024秋 德惠市期中)为了促进教育事业的发展,某县加强了对教育经费的投入,2022年共计投入3.4亿元,预计2024年投入4.9亿元,设教育经费的年平均增长率为x,下面所列方程正确的是( )
A.3.4(1+x)2=4.9
B.3.4x2=5
C.3.4(1+x%)2=4.9
D.3.4(1+x)2+3.4(1+x)=4.9
【解答】解:由题意可得,
3.4(1+x)2=4.9,
故选:A.
5.(2024春 馆陶县期中)嘉嘉的一面圆形镜子摔碎了,想配一面与原来大小相同的镜子,她把三角板的30°顶点A放在圆上,将两边与圆的交点分别记为点B,C,如图所示,经测量弦BC的长为6cm,则该镜子的直径为( )
A.6cm B.9cm C.12cm D.15cm
【解答】解:如图所示,作AB、BC的垂直平分线,交点即为圆心O,连接OC,OB,
∵∠A=30°,
∴∠COB=2∠A=60°,
又∵OC=OB,
∴△OCB是等边三角形,
∴OB=6cm,
∴该镜子的直径为12cm,
故选:C.
6.(2024春 馆陶县期中)如图是某同学自制的一个乒乓球拍,正面是半径为8cm的⊙O,劣弧的长为4πcm,阴影部分需要粘贴胶度,则胶皮的面积为( )
A.(32+48π)cm2 B.(16π﹣32)cm2
C.64πcm2 D.(48π﹣32)cm2
【解答】解:连接OA、OB.
设⊙O的半径为R,则R=8cm.
设∠AOB=n°,根据题意,得劣弧=×2πR,
解得n=90°,
∴S扇形AOB=×πR2=16π(cm2),SRt△AOB=OA OB=R2=32(cm2),
∴S空白弓形=S扇形AOB﹣SRt△AOB=(16π﹣32)(cm2),
∴S阴影=S⊙O﹣S空白弓形=πR2﹣(16π﹣32)=(32+48π)(cm2).
故选:A.
7.(2024春 上城区校级期中)如图,已知AB为⊙O的直径,弦CD与AB交于点E,连结OD、BC,设∠AOD=α,∠B=β,则∠AED=( )
A.α+β B. C.180﹣α﹣β D.
【解答】解:∵∠AOD=α,
∴∠BOD=180°﹣∠AOD=180°﹣α,
由圆周角定理得,∠BCD=,
在△BCE中,∠BEC=180°﹣∠BCD﹣∠B=180°﹣=,
∴∠AED=∠BEC=,
故选:B.
8.(2024春 秀英区校级期中)如图,⊙O的直径AB是4,弦CE交AB于点D.当D为AO的中点时,记CE的最小值为a,当∠CDB=60°时,记CE的最小值为b,则a﹣b的值为( )
A. B. C. D.
【解答】解:当D为AO的中点时,CE的最小值为a,此时CE⊥AB,如图1,连接OC,
∵D为OA的中点,OA、OC为⊙O的半径,⊙O的直径AB为4,
∴CD=CE,OA=OC=AB=2,
∴OD==AO=1,
根据勾股定理可得:CD==,
∴此时CE的最小值a=2CD=;
当∠CDB=60°时,此时点D、E与点A重合,即CE即为CA,如图2,连接OC,
∵∠CDB=60°,OA=OC=2,
∴△OAC是等边三角形,
∴AC=OA=2.
∴此时CE的最小值b=2;
∴a﹣b=﹣2,
故选C.
二.填空题(共8小题)
9.(2024春 沙坡头区校级期中)已知关于x的一元二次方程2x2﹣4x﹣1+k=0有两个相等的实数根,则k的值是 3 .
【解答】解:∵一元二次方程2x2﹣4x﹣1+k=0有两个相等的实数根,
∴Δ=(﹣4)2﹣4×2×(k﹣1)=0,
解得:k=3;
故答案为:3.
10.(2024春 博望区校级期中)一元二次方程2x2﹣7x﹣4=0的两根为x1,x2,则= .
【解答】解:∵一元二次方程2x2﹣7x﹣4=0的两根为x1,x2,
∴,
∴,
故答案为:.
11.(2024秋 东莞市期中)泉泉自制了一款等腰三角形晾衣架,设计的平面图如图所示,已知该晾衣架的底边长为30cm,另外两边长是方程x2﹣bx+400=0的两个根,则该晾衣架三角形部分的周长为 70 cm.
【解答】解:令等腰三角形的腰长为a cm,
因为等腰三角形的两条腰长是方程x2﹣bx+400=0的两个根,
所以a2=400,
则a=20(舍负),
即晾衣架的两条腰长都为20cm.
又因为该晾衣架的底边长为30cm,
所以该晾衣架三角形部分的周长为70cm.
故答案为:70.
12.(2024春 双流区校级期中)如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根x1,x2,且|x1﹣x2|=1,那么称这样的方程为“邻近根方程”,例如,一元二次方程x2+x=0的两个根是x1=0,x2=﹣1,|0﹣(﹣1)|=1,则方程x2+x=0是“邻近根方程”.若关于x的方程ax2+bx+2=0(a,b是常数,且a>0)是“邻近根方程”,令t=b2﹣4a2,则t的最大值为 .
【解答】解:设方程ax2+bx+2=0的两个根为x1,x2,
∴,
∵关于x的方程ax2+bx+2=0是“邻近根方程”,
∴|x1﹣x2|=1,
∴,
∴,
∴,
整理得:b2=a2+8a,
∴t=b2﹣4a2
=a2+8a﹣4a2
=﹣3a2+8a
=,
∵﹣3<0,
∴,
故答案为:.
13.(2023秋 江都区校级期中)若圆锥的底面圆半径为3,母线长为5,则该圆锥的侧面积是 15π .(结果保留π)
【解答】解:根据圆锥的侧面积公式:πrl=π×3×5=15π,
故答案为:15π.
14.(2023秋 西乡塘区校级期中)如图,四边形ABCD是⊙O的内接四边形,∠A=50°,则∠C的度数是 130° .
【解答】解:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠C=180°,
∵∠A=50°,
∴∠C=130°,
故答案为:130°.
15.(2023秋 赛罕区校级期中)如图,点A,B,C,D都在直径为的⊙O上,若OA⊥BC,∠CDA=27°,则阴影部分扇形的面积是 .
【解答】解:∵OA⊥BC,
∴,
∴∠AOB=2∠CDA=54°,
∴.
故答案为:.
16.(2024秋 九台区期中)日常生活中常见的装饰盘由圆盘和支架组成(如图1),它可以看作如图2所示的几何图形.已知AC=BD=5cm,AC⊥CD,垂足为点C,BD⊥CD,垂足为点D,CD=16cm,⊙O的半径r=10cm,则圆盘离桌面CD最近的距离是 1cm .
【解答】解:如图2,连接AB,OA,过点O作OG⊥CD于点G,交AB于点E,交⊙O于点F.
∵AC⊥CD,BD⊥CD,
∴AC∥BD,
∵AC=BD,
∴四边形ACDB是平行四边形,
∵∠ACD=90°,
∴四边形ACDB是矩形,
∴AB∥CD,AB=CD=16cm,
∵OG⊥CD,
∴OG⊥AB,
∴AE=EB=8cm,
∴OE===6(cm),
∴EF=OF﹣OE=10﹣6=4(cm),
∵EG=AC=BD=5cm,
∴FG=EG﹣EF=5﹣4=1(cm),
∴圆盘离桌面CD最近的距离是1cm,
故答案为:1cm.
三.解答题(共8小题)
17.(2024春 张店区校级期中)解方程:
(1)x2﹣14x+21=0.
(2)3x2﹣6x=4(x﹣2).
【解答】解:(1)∵x2﹣14x+21=0,
∴x2﹣14x=﹣21,
∴x2﹣14x+49=﹣21+49,
即(x﹣7)2=28,
∴,
∴,;
(2)移项提取公因式得,3x(x﹣2)﹣4(x﹣2)=0,
因式分解得,(x﹣2)(3x﹣4)=0,
∴x﹣2=0或3x﹣4=0,
∴x1=2,.
18.(2024秋 东莞市期中)若关于x的一元二次方程x2﹣2(m+1)x+m2+5=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2恰好是对角线长为6的矩形的相邻两边的边长,求这个矩形的周长.
【解答】解:(1)根据题意,得:Δ=[﹣2(m+1)]2﹣4(m2+5)=8m﹣16≥0,
解得:m≥2;
(2)由根与系数的关系可知x1+x2=2(m+1),,
∵x1,x2恰好是对角线长为6的矩形的相邻两边的边长,
∴,
整理,得m2+4m﹣21=0,
∴m1=3,m2=﹣7,
又∵m≥2,且x1+x2=2(m+1)>0,
∴m=3,
∴这个矩形的周长为:
2(x1+x2)=4(m+1)=16.
19.(2024春 睢宁县期中)问题:当a≠b时,判断a2+b2与2ab的大小关系.
(1)①小明说,当a>b>0时,可以构造如图所示的长方形ABCD,它是由1个正方形ABFE和1个长方形EFCD拼成.请你完成下面的推理过程.
②当b>a>0时,请你类比小明的思路,完成构图和推理.
(2)小红说,可以用“作差法”比较a2+b2与2ab的大小.请你尝试根据她的思路解决问题.
【解答】解:(1)①推理如下:
∵S长方形ABCD=a(a﹣b)=a2﹣ab,S长方形EFCD=b(a﹣b)=ab﹣b2,
由图形可得S长方形ABCD>S长方形EFCD,
∴a2﹣ab>ab﹣b2,
∴a2+b2>2ab;
②构造的图形如下:
推理如下:
∵S长方形ABCD=b(b﹣a)=b2﹣ab,S长方形EFCD=a(b﹣a)=ab﹣a2,
由图形可得S长方形ABCD>S长方形EFCD,
∴b2﹣ab>ab﹣a2,
∴a2+b2>2ab;
(2)作差可得,a2+b2﹣2ab=(a﹣b)2,
∵a≠b,
∴(a﹣b)2>0,
∴a2+b2﹣2ab>0,
∴a2+b2>2ab.
20.(2022秋 麻阳县期中)云南某地一村民,2021年承包种植橙子树200亩,由于第一年收成不错,该村民每年都增加种植面积,到2023年共种植288亩.假设每年的增长率相同.
(1)求该村民这两年种植橙子亩数的平均增长率.
(2)某水果批发店销售该种橙子,市场调查发现,当橙子售价为18元/千克时,每天能售出120千克,售价每降低1元,每天可多售出15千克,为了减少库存,该店决定降价促销,已知该橙子的平均成本价为8元/千克,若使销售该种橙子每天获利840元,则售价应降低多少元?
【解答】解:(1)设该村民这两年种植橙子亩数的平均增长率为x,
根据题意得:200(1+x)2=288,
解得:x1=0.2=20%,x2=﹣2.2(不符合题意,舍去).
答:该村民这两年种植橙子亩数的平均增长率为20%;
(2)设售价应降价y元,则每千克的销售利润为(18﹣y﹣8)元,每天能售出(120+15y)千克,
根据题意得:(18﹣y﹣8)(120+15y)=840,
整理得:y2﹣2y﹣24=0,
解得:y1=6,y2=﹣4(不符合题意,舍去).
答:售价应降低6元.
21.(2024春 静安区校级期中)公园里有一块面积为10平方米的正方形绿化地,现在这块地上划出一个扇形区域举办花展,并在扇形的周边围上低矮的篱笆,如图所示,正方形ABCD为绿化地,扇形EAF为所划区域,AF=4FD,求需要多长的篱笆.(,结果精确到十分位)
【解答】解:∵公园里有一块面积为10平方米的正方形ABCD绿化地,
∴米,
∵AF=4FD,AD+DF=AD,
∴米,
∵扇形EAF为所划区域,
∴米,扇形的周长=(米),
∴需要的篱笆长度=(米),
∴需要9.1米的篱笆.
22.(2024春 钢城区期中)如图,在△ABC中,O是边AD上的一点,以点O为圆心,OD的长为半径.⊙O恰好与边AB相切于点B,与边AD交于点C,连接BC.
(1)求证:∠ABC=∠D;
(2)若AB=5,AC=3,求⊙O的半径.
【解答】(1)证明:连接OB,
∵AB与⊙O相切于B,
∴OB⊥AB,
∴∠ABC+∠CBO=90°,
∵CD是圆的直径,
∴∠CBD=90°,
∴∠D+∠OCB=90°,
∵OC=OB,
∴∠OCB=∠OBC,
∴∠ABC=∠D;
(2)解:∵∠D=∠ABC,
∵∠CAB=∠BAD,
∴△ABC∽△ADB,
∴AB:AD=AC:AB,
∵AB=5,AC=3,
∴5:AD=3:5,
∴AD=,
∴CD=AD﹣AC=,
∴⊙O的半径是CD=.
23.(2024春 兴庆区校级期中)如图,Rt△ABC中,∠ACB=90°,CD为斜边中线,以CD为直径作⊙O交BC于点E,过点E作EF⊥AB,垂足为点F.
(1)求证:EF为⊙O的切线;
(2)若直径CD=13,CB=24,求EF的长.
【解答】(1)证明:连接OE,如图所示:
∵以CD为直径作⊙O交BC于点E,
∴OC=OE,
∴∠OCE=∠OEC,
∵在Rt△ABC中,∠ACB=90°,CD为斜边中线,
∴CD=AD=BD,
∴∠OCE=∠B,
∴∠OEC∠B,
∴OE∥AB,
∵EF⊥AB,
∴OE⊥EF,
又∵OE为⊙O半径,
EF为⊙O的切线;
(2)解:∵CD=13,CB=24,
∴AD=BD=CD=13,
∴AB=26,
在Rt△ABC中,∠ACB=90°,
由勾股定理得:AC==10,
∵AD为⊙O直径,
∴OC=OD,
又∵OE∥AB,
∴OE为△CDB的中位线,
∴CE=BE=CB=12,
∵EF⊥AB,∠ACB=90°,
∴∠EFB=∠ACB=90°,
又∵∠B=∠B,
∴△BEF∽△BAC,
∴EF:AC=BE:AB,
即EF:10=12:26,
∴EF=.
24.(2024春 东西湖区期中)如图,⊙O中,.
(1)如图1,分别以AB,BC为边作平行四边形ABCD,求证:AD是⊙O的切线;
(2)如图2,若∠C=75°,BC=4,求出阴影部分的面积(结果保留π和根号).
【解答】(1)证明:连接AO,并延长交BC于点E,如图,
∵,
∴AE⊥BC,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴OA⊥AD.
∵OA为⊙O的半径,
∴AD是⊙O的切线;
(2)解:连接OB,OC,连接AO,并延长交BC于点D,如图,
∵,
∴AB=AC,AD⊥BC,
∴∠ABC=∠ACB=75°,
∴∠BAC=30°,
∴∠BOC=2∠BAC=60°.
∵OB=OC,
∴△OBC为等边三角形,
∴OB=OC=BC=4,
∴OA=OB=4.
∵OD⊥BC,
∴BD=DC=2,
∴OD==2.
∴AD=OA+OD=4+2.
∴BC AD=4×(4+2)=8+4.
∵S弓形BEC=S扇形OBC﹣S△OBC==π﹣4,
∴S阴影=S弓形BEC+S△ABC=+8.
同课章节目录
