第2章对称图形-圆期中重组训练(含详解)2024—2025学年苏科版数学九年级上册
文档属性
| 名称 | 第2章对称图形-圆期中重组训练(含详解)2024—2025学年苏科版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 408.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 19:10:54 | ||
图片预览



文档简介
第2章对称图形-圆期中重组训练-2024-2025学年数学九年级上册苏科版
一.选择题(共8小题)
1.(2023秋 兰山区校级期中)小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定是错误的是( )
A.4 B.5 C.10 D.11
2.(2023秋 亭湖区校级期中)已知⊙O的半径为3,当OP=5时,点P与⊙O的位置关系为( )
A.点在圆内 B.点在圆外 C.点在圆上 D.不能确定
3.(2019秋 魏都区校级期中)下列语句中:①过三点能作一个圆;②平分弦的直径垂直于弦;③长度相等的弧是等弧;④经过圆心的每一条直线都是圆的对称轴;⑤相等的圆心角所对的弧度数相等.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
4.(2023秋 厦门期中)如图,OE⊥AB于E,若⊙O的直径为10cm,OE=3cm,则AB长为( )
A.4cm B.5cm C.6cm D.8cm
5.(2023秋 新市区校级期中)如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A.25° B.40° C.30° D.50°
6.(2023秋 诸城市期中)如图,在⊙O中,∠A=30°,劣弧的度数是( )
A.30° B.60° C.90° D.120°
7.(2023秋 朝阳区校级期中)如图,点A,B,C均在⊙O上,∠BOC=100°,则∠BAC的度数为( )
A.70° B.60° C.50° D.40°
8.(2023秋 玄武区校级期中)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90° B.100° C.110° D.120°
二.填空题(共8小题)
9.(2023秋 泰兴市期中)⊙O半径为4,点A到点O距离为3,则点A在⊙O (填“上”“内”或“外”).
10.(2023秋 婺城区校级期中)已知点P为平面内一点,若点P到⊙O上的点的最长距离为5,最短距离为1,则⊙O的半径为 .
11.(2023秋 西城区校级期中)蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为 m.
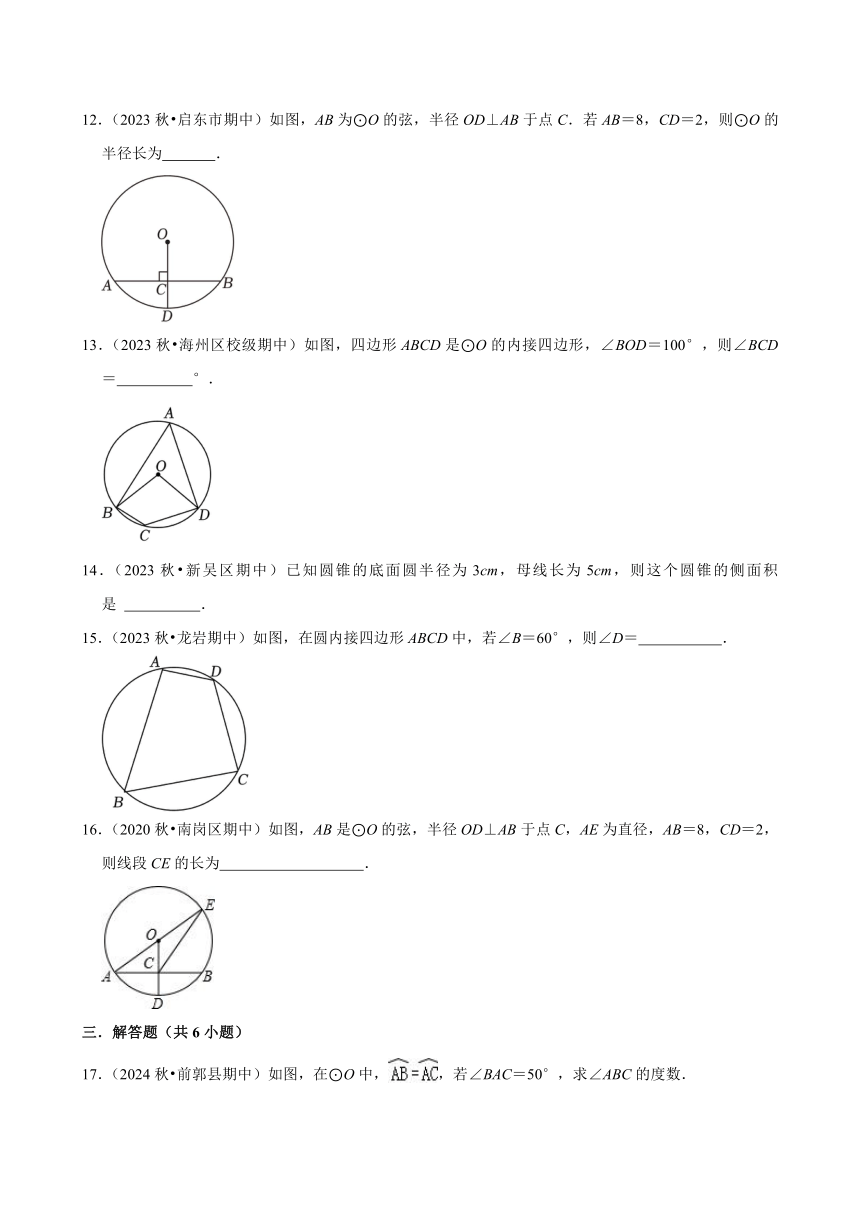
12.(2023秋 启东市期中)如图,AB为⊙O的弦,半径OD⊥AB于点C.若AB=8,CD=2,则⊙O的半径长为 .
13.(2023秋 海州区校级期中)如图,四边形ABCD是⊙O的内接四边形,∠BOD=100°,则∠BCD= °.
14.(2023秋 新吴区期中)已知圆锥的底面圆半径为3cm,母线长为5cm,则这个圆锥的侧面积是 .
15.(2023秋 龙岩期中)如图,在圆内接四边形ABCD中,若∠B=60°,则∠D= .
16.(2020秋 南岗区期中)如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为 .
三.解答题(共6小题)
17.(2024秋 前郭县期中)如图,在⊙O中,,若∠BAC=50°,求∠ABC的度数.
18.(2023秋 莱西市校级期中)小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
19.(2024春 沙坡头区校级期中)如图,AB是⊙O的直径,点C为⊙O上一点,连接BC,点D在BA的延长线上,点E在OB上,过点E作BD的垂线分别交DC的延长线于点F,交BC于点G,且∠F=2∠B.(1)求证:DF是⊙O的切线;
(2)求证:FC=FG;
(3)若AO=2AD=10,E为OB的中点,求GE的长.
20.(2023秋 香坊区期中)如图,AB是⊙O的直径,AC是弦,D是的中点,CD与AB交于点E.F是AB延长线上的一点,且CF=EF.
(1)求证:CF为⊙O的切线;
(2)连接BD.若CF=4,BF=2,求BD的长.
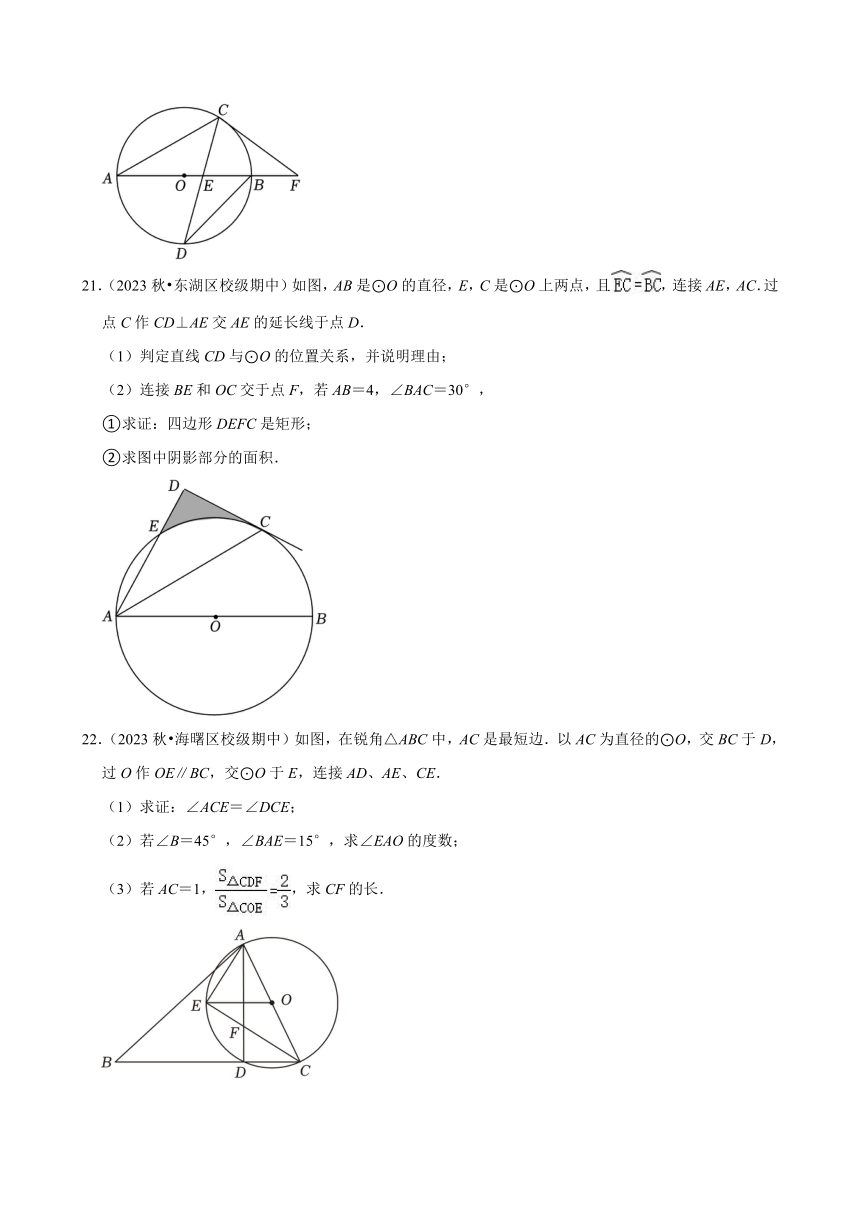
21.(2023秋 东湖区校级期中)如图,AB是⊙O的直径,E,C是⊙O上两点,且,连接AE,AC.过点C作CD⊥AE交AE的延长线于点D.
(1)判定直线CD与⊙O的位置关系,并说明理由;
(2)连接BE和OC交于点F,若AB=4,∠BAC=30°,
①求证:四边形DEFC是矩形;
②求图中阴影部分的面积.
22.(2023秋 海曙区校级期中)如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交⊙O于E,连接AD、AE、CE.
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=1,,求CF的长.
第2章对称图形-圆期中重组训练-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2023秋 兰山区校级期中)小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定是错误的是( )
A.4 B.5 C.10 D.11
【解答】解:∵半径为5的圆,直径为10,
∴在半径为5的圆中测量弦AB的长度,AB的取值范围是:0<AB≤10,
∴弦AB的长度可以是4,5,10,不可能为11.
故选:D.
2.(2023秋 亭湖区校级期中)已知⊙O的半径为3,当OP=5时,点P与⊙O的位置关系为( )
A.点在圆内 B.点在圆外 C.点在圆上 D.不能确定
【解答】解:∵OP=5、r=3,
∴OP>r,
则点P在⊙O外,
故选:B.
3.(2019秋 魏都区校级期中)下列语句中:①过三点能作一个圆;②平分弦的直径垂直于弦;③长度相等的弧是等弧;④经过圆心的每一条直线都是圆的对称轴;⑤相等的圆心角所对的弧度数相等.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①经过不在同一条直线上的三点可以确定一个圆,故本小题错误;
②平分弦(非直径)的直径垂直于弦,故本小题错误;
③长度相等的弧不一定是等弧,故本小题错误;
④经过圆心的每一条直线都是圆的对称轴,符合圆的性质,故本小题正确;
⑤相等的圆心角所对的弧度数相等,故本小题正确.
故选:B.
4.(2023秋 厦门期中)如图,OE⊥AB于E,若⊙O的直径为10cm,OE=3cm,则AB长为( )
A.4cm B.5cm C.6cm D.8cm
【解答】解:连接OA,如图所示,
∵⊙O的直径为10cm,
∴OA=5cm,
∵OE⊥AB于E,
∴AE=AB,
在Rt△AOE中,OE=3cm,
∴AE===4(cm),
∴AB=2×4=8(cm),
故选:D.
5.(2023秋 新市区校级期中)如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A.25° B.40° C.30° D.50°
【解答】解:∵过点D的弦DE平行于半径OA,即OA∥DE,
∴∠D=∠AOD=50°,
∵OA=OC,
∴∠ACO=∠OAC=∠AOD=25°.
故选:A.
6.(2023秋 诸城市期中)如图,在⊙O中,∠A=30°,劣弧的度数是( )
A.30° B.60° C.90° D.120°
【解答】解:连接OB.
∵OA=OB,
∴∠A=∠B=30°,
∴∠AOB=180°﹣30°﹣30°=120°,
∴的度数为120°.
故选:D.
7.(2023秋 朝阳区校级期中)如图,点A,B,C均在⊙O上,∠BOC=100°,则∠BAC的度数为( )
A.70° B.60° C.50° D.40°
【解答】解:∵∠BAC为所对的圆周角,∠BOC为所对的圆心角,
∴∠BAC=∠BOC=×100°=50°.
故选:C.
8.(2023秋 玄武区校级期中)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90° B.100° C.110° D.120°
【解答】解:连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠ACE=20°,
∴∠ADE=∠ACE=20°,
∴∠BDE=∠ADB+∠ADE=110°,
故选:C.
二.填空题(共8小题)
9.(2023秋 泰兴市期中)⊙O半径为4,点A到点O距离为3,则点A在⊙O 内 (填“上”“内”或“外”).
【解答】解:∵⊙O的半径r=4,且点A到圆心O的距离d=3,
∴d<r,
∴点A在⊙O内,
故答案为:内.
10.(2023秋 婺城区校级期中)已知点P为平面内一点,若点P到⊙O上的点的最长距离为5,最短距离为1,则⊙O的半径为 2或3 .
【解答】解:当点P在圆内时,则直径=5+1=6,因而半径是3;
当点P在圆外时,直径=5﹣1=4,因而半径是2.
所以⊙O的半径为2或3.
故答案为:2或3.
11.(2023秋 西城区校级期中)蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为 4 m.
【解答】解:∵CD垂直平分AB,
∴AD=8.
∴OD==6m,
∴CD=OC﹣OD=10﹣6=4(m).
故答案为:4.
12.(2023秋 启东市期中)如图,AB为⊙O的弦,半径OD⊥AB于点C.若AB=8,CD=2,则⊙O的半径长为 5 .
【解答】解:∵⊙O的弦AB=8,半径OD⊥AB,
∴AC=AB=×8=4,
设⊙O的半径为r,则OC=r﹣CD=r﹣2,连接OA,
在Rt△OAC中,
OA2=OC2+AC2,即r2=(r﹣2)2+42,解得r=5.
故答案为:5.
13.(2023秋 海州区校级期中)如图,四边形ABCD是⊙O的内接四边形,∠BOD=100°,则∠BCD= 130 °.
【解答】解:∵∠BOD=100°,
∴∠A=50°.
∵四边形ABCD是圆内接四边形,
∴∠BCD=180°﹣50°=130°.
故答案为:130.
14.(2023秋 新吴区期中)已知圆锥的底面圆半径为3cm,母线长为5cm,则这个圆锥的侧面积是 15π .
【解答】解:圆锥的侧面展开图面积=×2π×3×5=15π(cm2).
故答案为:15π.
15.(2023秋 龙岩期中)如图,在圆内接四边形ABCD中,若∠B=60°,则∠D= 120° .
【解答】解:∵四边形ABCD是圆内接四边形,
∴∠B+∠D=180°,
∵∠B=60°,
∴∠D=120°,
故答案为:120°.
16.(2020秋 南岗区期中)如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为 2 .
【解答】解:连接BE,如图所示:
∵OD⊥AB,AB=8,
∴AC=AB=4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,由勾股定理得:r2=(r﹣2)2+42,
解得:r=5,
∴AE=2r=10;
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2,
故答案为:2.
三.解答题(共6小题)
17.(2024秋 前郭县期中)如图,在⊙O中,,若∠BAC=50°,求∠ABC的度数.
【解答】解:∵,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=50°,∠ABC+∠ACB+∠BAC=180°,
∴∠ABC=∠ACB=(180°﹣50°)=65°.
18.(2023秋 莱西市校级期中)小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
【解答】解:①分别以A、B为圆心,以大于AB为半径画圆,两圆相交于D、E两点,连接DE;
②分别以A、C为圆心,以大于AC为半径画圆,两圆相交于G、F两点,连接GF;
③直线DE与GF相交于点O,以O为圆心,以OA的长为半径画圆,则此圆即为花坛的位置.
19.(2024春 沙坡头区校级期中)如图,AB是⊙O的直径,点C为⊙O上一点,连接BC,点D在BA的延长线上,点E在OB上,过点E作BD的垂线分别交DC的延长线于点F,交BC于点G,且∠F=2∠B.(1)求证:DF是⊙O的切线;
(2)求证:FC=FG;
(3)若AO=2AD=10,E为OB的中点,求GE的长.
【解答】(1)证明:连接OC,则OB=OC,
∴∠B=∠OCB,
∴∠DOC=2∠B,
∵∠F=2∠B,
∴∠DOC=∠F,
∵EF⊥BD,
∴∠D+∠F=90°,则∠D+∠DOC=90°,
∴∠OCD=90°,
又∵点C在⊙O上,
∴DF是⊙O的切线;
(2)证明:∵点C是⊙O的切点,
∴∠OCF=∠OCB+∠FCB=90°,
∵OC=OB,
∴∠OCB=∠OBC.
又∵FE⊥OB,
∴∠GEB=90°,∠OBC+∠EGB=90°,
∴∠FCB=∠EGB,
又∵∠EGB=∠FGC,
∴∠FCB=∠FGC,
∴F C=F G;
(3)解:∵AO=2AD=10,
∴AD=5,OC=OB=10,
∴OD=15,由(1)得∠OCD=90°,
在Rt△OCD中,由勾股定理得.
∵点E为OB的中点,
∴OE=BE=5,
∴DE=20.
∵∠OCD=∠DEF,∠D=∠D,
∴△OCD∽△FED,
∴,
∴,
∴,,
∴,
∴,
∴.
20.(2023秋 香坊区期中)如图,AB是⊙O的直径,AC是弦,D是的中点,CD与AB交于点E.F是AB延长线上的一点,且CF=EF.
(1)求证:CF为⊙O的切线;
(2)连接BD.若CF=4,BF=2,求BD的长.
【解答】(1)如图,连接OC,OD,
∵OC=OD,
∴∠OCD=∠ODC,
∵CF=EF,
∴∠FCE=∠FEC,
∵∠OED=∠FEC,
∴∠OED=∠FCE,
∵AB是直径,D是的中点,
∴∠DOE=90°,
∴∠OED+∠ODC=90°,
∴∠FCE+∠OCD=90°,即∠OCF=90°,
∵OC是半径,
∴CF是⊙O的切线.
(2)设OA=OD=OC=OB=r,则OF=r+2,
在Rt△COF中,OC2+CF2=OF2
∴42+r2=(r+2)2,
解得r=3,
∴OB=OD=3,
∵∠DOB=90°,
∴BD2=OD2+OB2,
∴.
21.(2023秋 东湖区校级期中)如图,AB是⊙O的直径,E,C是⊙O上两点,且,连接AE,AC.过点C作CD⊥AE交AE的延长线于点D.
(1)判定直线CD与⊙O的位置关系,并说明理由;
(2)连接BE和OC交于点F,若AB=4,∠BAC=30°,
①求证:四边形DEFC是矩形;
②求图中阴影部分的面积.
【解答】(1)解:直线CD与⊙O相切,
理由:连接OC,
∵,
∴∠CAD=∠BAC,
∵OA=OC,
∴∠BAC=∠ACO,
∴∠CAD=∠ACO,
∴AD∥OC,
∵AD⊥CD,
∴OC⊥CD,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)①证明:∵,
∴OC⊥CE,BF=EF,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠FED=∠D=∠EFC=90°,
∴四边形DEFC是矩形;
②解:∵,
∴∠COE=∠BOC=2∠BAC=60°,
在Rt△OEF中,OE=AB=2,
∴∠OEF=90°﹣∠COE=30°,
∴OF=OE=1,
∴CF=OC﹣OE=1=DE,
∴EF===CD,
∴S梯形OCDE=(DE+OC) CD=,
S扇形OCE==,
∴图中阴影部分的面积=S梯形OCDE﹣S扇形OCE=﹣.
22.(2023秋 海曙区校级期中)如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交⊙O于E,连接AD、AE、CE.
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=1,,求CF的长.
【解答】(1)证明:∵OC=OE,
∴∠OEC=∠OCE,
∵OE∥BC,
∴∠OEC=∠ECD,
∴∠OCE=∠ECD,
即∠ACE=∠DCE,
(2)解:延长AE交BC于点G,
∵∠AGC是△ABG的外角,
∴∠AGC=∠B+∠BAG=60°,
∵OE∥BC,
∴∠AEO=∠AGC=60°,
∵OA=OE,
∴∠EAO=∠AEO=60°;
(3)解:∵O是AC中点
∴,
∵,
∴=,
∵AC是直径,
∴∠AEC=∠FDC=90°,
∵∠ACE=∠FCD,
∴△CDF∽△CEA,
∴=,
∴CF=CA=.
一.选择题(共8小题)
1.(2023秋 兰山区校级期中)小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定是错误的是( )
A.4 B.5 C.10 D.11
2.(2023秋 亭湖区校级期中)已知⊙O的半径为3,当OP=5时,点P与⊙O的位置关系为( )
A.点在圆内 B.点在圆外 C.点在圆上 D.不能确定
3.(2019秋 魏都区校级期中)下列语句中:①过三点能作一个圆;②平分弦的直径垂直于弦;③长度相等的弧是等弧;④经过圆心的每一条直线都是圆的对称轴;⑤相等的圆心角所对的弧度数相等.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
4.(2023秋 厦门期中)如图,OE⊥AB于E,若⊙O的直径为10cm,OE=3cm,则AB长为( )
A.4cm B.5cm C.6cm D.8cm
5.(2023秋 新市区校级期中)如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A.25° B.40° C.30° D.50°
6.(2023秋 诸城市期中)如图,在⊙O中,∠A=30°,劣弧的度数是( )
A.30° B.60° C.90° D.120°
7.(2023秋 朝阳区校级期中)如图,点A,B,C均在⊙O上,∠BOC=100°,则∠BAC的度数为( )
A.70° B.60° C.50° D.40°
8.(2023秋 玄武区校级期中)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90° B.100° C.110° D.120°
二.填空题(共8小题)
9.(2023秋 泰兴市期中)⊙O半径为4,点A到点O距离为3,则点A在⊙O (填“上”“内”或“外”).
10.(2023秋 婺城区校级期中)已知点P为平面内一点,若点P到⊙O上的点的最长距离为5,最短距离为1,则⊙O的半径为 .
11.(2023秋 西城区校级期中)蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为 m.
12.(2023秋 启东市期中)如图,AB为⊙O的弦,半径OD⊥AB于点C.若AB=8,CD=2,则⊙O的半径长为 .
13.(2023秋 海州区校级期中)如图,四边形ABCD是⊙O的内接四边形,∠BOD=100°,则∠BCD= °.
14.(2023秋 新吴区期中)已知圆锥的底面圆半径为3cm,母线长为5cm,则这个圆锥的侧面积是 .
15.(2023秋 龙岩期中)如图,在圆内接四边形ABCD中,若∠B=60°,则∠D= .
16.(2020秋 南岗区期中)如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为 .
三.解答题(共6小题)
17.(2024秋 前郭县期中)如图,在⊙O中,,若∠BAC=50°,求∠ABC的度数.
18.(2023秋 莱西市校级期中)小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
19.(2024春 沙坡头区校级期中)如图,AB是⊙O的直径,点C为⊙O上一点,连接BC,点D在BA的延长线上,点E在OB上,过点E作BD的垂线分别交DC的延长线于点F,交BC于点G,且∠F=2∠B.(1)求证:DF是⊙O的切线;
(2)求证:FC=FG;
(3)若AO=2AD=10,E为OB的中点,求GE的长.
20.(2023秋 香坊区期中)如图,AB是⊙O的直径,AC是弦,D是的中点,CD与AB交于点E.F是AB延长线上的一点,且CF=EF.
(1)求证:CF为⊙O的切线;
(2)连接BD.若CF=4,BF=2,求BD的长.
21.(2023秋 东湖区校级期中)如图,AB是⊙O的直径,E,C是⊙O上两点,且,连接AE,AC.过点C作CD⊥AE交AE的延长线于点D.
(1)判定直线CD与⊙O的位置关系,并说明理由;
(2)连接BE和OC交于点F,若AB=4,∠BAC=30°,
①求证:四边形DEFC是矩形;
②求图中阴影部分的面积.
22.(2023秋 海曙区校级期中)如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交⊙O于E,连接AD、AE、CE.
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=1,,求CF的长.
第2章对称图形-圆期中重组训练-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2023秋 兰山区校级期中)小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定是错误的是( )
A.4 B.5 C.10 D.11
【解答】解:∵半径为5的圆,直径为10,
∴在半径为5的圆中测量弦AB的长度,AB的取值范围是:0<AB≤10,
∴弦AB的长度可以是4,5,10,不可能为11.
故选:D.
2.(2023秋 亭湖区校级期中)已知⊙O的半径为3,当OP=5时,点P与⊙O的位置关系为( )
A.点在圆内 B.点在圆外 C.点在圆上 D.不能确定
【解答】解:∵OP=5、r=3,
∴OP>r,
则点P在⊙O外,
故选:B.
3.(2019秋 魏都区校级期中)下列语句中:①过三点能作一个圆;②平分弦的直径垂直于弦;③长度相等的弧是等弧;④经过圆心的每一条直线都是圆的对称轴;⑤相等的圆心角所对的弧度数相等.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①经过不在同一条直线上的三点可以确定一个圆,故本小题错误;
②平分弦(非直径)的直径垂直于弦,故本小题错误;
③长度相等的弧不一定是等弧,故本小题错误;
④经过圆心的每一条直线都是圆的对称轴,符合圆的性质,故本小题正确;
⑤相等的圆心角所对的弧度数相等,故本小题正确.
故选:B.
4.(2023秋 厦门期中)如图,OE⊥AB于E,若⊙O的直径为10cm,OE=3cm,则AB长为( )
A.4cm B.5cm C.6cm D.8cm
【解答】解:连接OA,如图所示,
∵⊙O的直径为10cm,
∴OA=5cm,
∵OE⊥AB于E,
∴AE=AB,
在Rt△AOE中,OE=3cm,
∴AE===4(cm),
∴AB=2×4=8(cm),
故选:D.
5.(2023秋 新市区校级期中)如图,已知CD为⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50°,则∠C的度数是( )
A.25° B.40° C.30° D.50°
【解答】解:∵过点D的弦DE平行于半径OA,即OA∥DE,
∴∠D=∠AOD=50°,
∵OA=OC,
∴∠ACO=∠OAC=∠AOD=25°.
故选:A.
6.(2023秋 诸城市期中)如图,在⊙O中,∠A=30°,劣弧的度数是( )
A.30° B.60° C.90° D.120°
【解答】解:连接OB.
∵OA=OB,
∴∠A=∠B=30°,
∴∠AOB=180°﹣30°﹣30°=120°,
∴的度数为120°.
故选:D.
7.(2023秋 朝阳区校级期中)如图,点A,B,C均在⊙O上,∠BOC=100°,则∠BAC的度数为( )
A.70° B.60° C.50° D.40°
【解答】解:∵∠BAC为所对的圆周角,∠BOC为所对的圆心角,
∴∠BAC=∠BOC=×100°=50°.
故选:C.
8.(2023秋 玄武区校级期中)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠ACE=20°,则∠BDE的度数为( )
A.90° B.100° C.110° D.120°
【解答】解:连接AD,
∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠ACE=20°,
∴∠ADE=∠ACE=20°,
∴∠BDE=∠ADB+∠ADE=110°,
故选:C.
二.填空题(共8小题)
9.(2023秋 泰兴市期中)⊙O半径为4,点A到点O距离为3,则点A在⊙O 内 (填“上”“内”或“外”).
【解答】解:∵⊙O的半径r=4,且点A到圆心O的距离d=3,
∴d<r,
∴点A在⊙O内,
故答案为:内.
10.(2023秋 婺城区校级期中)已知点P为平面内一点,若点P到⊙O上的点的最长距离为5,最短距离为1,则⊙O的半径为 2或3 .
【解答】解:当点P在圆内时,则直径=5+1=6,因而半径是3;
当点P在圆外时,直径=5﹣1=4,因而半径是2.
所以⊙O的半径为2或3.
故答案为:2或3.
11.(2023秋 西城区校级期中)蔬菜基地圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则高度CD为 4 m.
【解答】解:∵CD垂直平分AB,
∴AD=8.
∴OD==6m,
∴CD=OC﹣OD=10﹣6=4(m).
故答案为:4.
12.(2023秋 启东市期中)如图,AB为⊙O的弦,半径OD⊥AB于点C.若AB=8,CD=2,则⊙O的半径长为 5 .
【解答】解:∵⊙O的弦AB=8,半径OD⊥AB,
∴AC=AB=×8=4,
设⊙O的半径为r,则OC=r﹣CD=r﹣2,连接OA,
在Rt△OAC中,
OA2=OC2+AC2,即r2=(r﹣2)2+42,解得r=5.
故答案为:5.
13.(2023秋 海州区校级期中)如图,四边形ABCD是⊙O的内接四边形,∠BOD=100°,则∠BCD= 130 °.
【解答】解:∵∠BOD=100°,
∴∠A=50°.
∵四边形ABCD是圆内接四边形,
∴∠BCD=180°﹣50°=130°.
故答案为:130.
14.(2023秋 新吴区期中)已知圆锥的底面圆半径为3cm,母线长为5cm,则这个圆锥的侧面积是 15π .
【解答】解:圆锥的侧面展开图面积=×2π×3×5=15π(cm2).
故答案为:15π.
15.(2023秋 龙岩期中)如图,在圆内接四边形ABCD中,若∠B=60°,则∠D= 120° .
【解答】解:∵四边形ABCD是圆内接四边形,
∴∠B+∠D=180°,
∵∠B=60°,
∴∠D=120°,
故答案为:120°.
16.(2020秋 南岗区期中)如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为 2 .
【解答】解:连接BE,如图所示:
∵OD⊥AB,AB=8,
∴AC=AB=4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,由勾股定理得:r2=(r﹣2)2+42,
解得:r=5,
∴AE=2r=10;
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2,
故答案为:2.
三.解答题(共6小题)
17.(2024秋 前郭县期中)如图,在⊙O中,,若∠BAC=50°,求∠ABC的度数.
【解答】解:∵,
∴AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=50°,∠ABC+∠ACB+∠BAC=180°,
∴∠ABC=∠ACB=(180°﹣50°)=65°.
18.(2023秋 莱西市校级期中)小明家的房前有一块矩形的空地,空地上有三棵树A、B、C,小明想建一个圆形花坛,使三棵树都在花坛的边上.请你帮小明把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹).
【解答】解:①分别以A、B为圆心,以大于AB为半径画圆,两圆相交于D、E两点,连接DE;
②分别以A、C为圆心,以大于AC为半径画圆,两圆相交于G、F两点,连接GF;
③直线DE与GF相交于点O,以O为圆心,以OA的长为半径画圆,则此圆即为花坛的位置.
19.(2024春 沙坡头区校级期中)如图,AB是⊙O的直径,点C为⊙O上一点,连接BC,点D在BA的延长线上,点E在OB上,过点E作BD的垂线分别交DC的延长线于点F,交BC于点G,且∠F=2∠B.(1)求证:DF是⊙O的切线;
(2)求证:FC=FG;
(3)若AO=2AD=10,E为OB的中点,求GE的长.
【解答】(1)证明:连接OC,则OB=OC,
∴∠B=∠OCB,
∴∠DOC=2∠B,
∵∠F=2∠B,
∴∠DOC=∠F,
∵EF⊥BD,
∴∠D+∠F=90°,则∠D+∠DOC=90°,
∴∠OCD=90°,
又∵点C在⊙O上,
∴DF是⊙O的切线;
(2)证明:∵点C是⊙O的切点,
∴∠OCF=∠OCB+∠FCB=90°,
∵OC=OB,
∴∠OCB=∠OBC.
又∵FE⊥OB,
∴∠GEB=90°,∠OBC+∠EGB=90°,
∴∠FCB=∠EGB,
又∵∠EGB=∠FGC,
∴∠FCB=∠FGC,
∴F C=F G;
(3)解:∵AO=2AD=10,
∴AD=5,OC=OB=10,
∴OD=15,由(1)得∠OCD=90°,
在Rt△OCD中,由勾股定理得.
∵点E为OB的中点,
∴OE=BE=5,
∴DE=20.
∵∠OCD=∠DEF,∠D=∠D,
∴△OCD∽△FED,
∴,
∴,
∴,,
∴,
∴,
∴.
20.(2023秋 香坊区期中)如图,AB是⊙O的直径,AC是弦,D是的中点,CD与AB交于点E.F是AB延长线上的一点,且CF=EF.
(1)求证:CF为⊙O的切线;
(2)连接BD.若CF=4,BF=2,求BD的长.
【解答】(1)如图,连接OC,OD,
∵OC=OD,
∴∠OCD=∠ODC,
∵CF=EF,
∴∠FCE=∠FEC,
∵∠OED=∠FEC,
∴∠OED=∠FCE,
∵AB是直径,D是的中点,
∴∠DOE=90°,
∴∠OED+∠ODC=90°,
∴∠FCE+∠OCD=90°,即∠OCF=90°,
∵OC是半径,
∴CF是⊙O的切线.
(2)设OA=OD=OC=OB=r,则OF=r+2,
在Rt△COF中,OC2+CF2=OF2
∴42+r2=(r+2)2,
解得r=3,
∴OB=OD=3,
∵∠DOB=90°,
∴BD2=OD2+OB2,
∴.
21.(2023秋 东湖区校级期中)如图,AB是⊙O的直径,E,C是⊙O上两点,且,连接AE,AC.过点C作CD⊥AE交AE的延长线于点D.
(1)判定直线CD与⊙O的位置关系,并说明理由;
(2)连接BE和OC交于点F,若AB=4,∠BAC=30°,
①求证:四边形DEFC是矩形;
②求图中阴影部分的面积.
【解答】(1)解:直线CD与⊙O相切,
理由:连接OC,
∵,
∴∠CAD=∠BAC,
∵OA=OC,
∴∠BAC=∠ACO,
∴∠CAD=∠ACO,
∴AD∥OC,
∵AD⊥CD,
∴OC⊥CD,
∵OC是⊙O的半径,
∴CD是⊙O的切线;
(2)①证明:∵,
∴OC⊥CE,BF=EF,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠FED=∠D=∠EFC=90°,
∴四边形DEFC是矩形;
②解:∵,
∴∠COE=∠BOC=2∠BAC=60°,
在Rt△OEF中,OE=AB=2,
∴∠OEF=90°﹣∠COE=30°,
∴OF=OE=1,
∴CF=OC﹣OE=1=DE,
∴EF===CD,
∴S梯形OCDE=(DE+OC) CD=,
S扇形OCE==,
∴图中阴影部分的面积=S梯形OCDE﹣S扇形OCE=﹣.
22.(2023秋 海曙区校级期中)如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交⊙O于E,连接AD、AE、CE.
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=1,,求CF的长.
【解答】(1)证明:∵OC=OE,
∴∠OEC=∠OCE,
∵OE∥BC,
∴∠OEC=∠ECD,
∴∠OCE=∠ECD,
即∠ACE=∠DCE,
(2)解:延长AE交BC于点G,
∵∠AGC是△ABG的外角,
∴∠AGC=∠B+∠BAG=60°,
∵OE∥BC,
∴∠AEO=∠AGC=60°,
∵OA=OE,
∴∠EAO=∠AEO=60°;
(3)解:∵O是AC中点
∴,
∵,
∴=,
∵AC是直径,
∴∠AEC=∠FDC=90°,
∵∠ACE=∠FCD,
∴△CDF∽△CEA,
∴=,
∴CF=CA=.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
