第十二章 全等三角形 复习试题(含答案) 2024--2025学年人教版八年级数学上册
文档属性
| 名称 | 第十二章 全等三角形 复习试题(含答案) 2024--2025学年人教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览

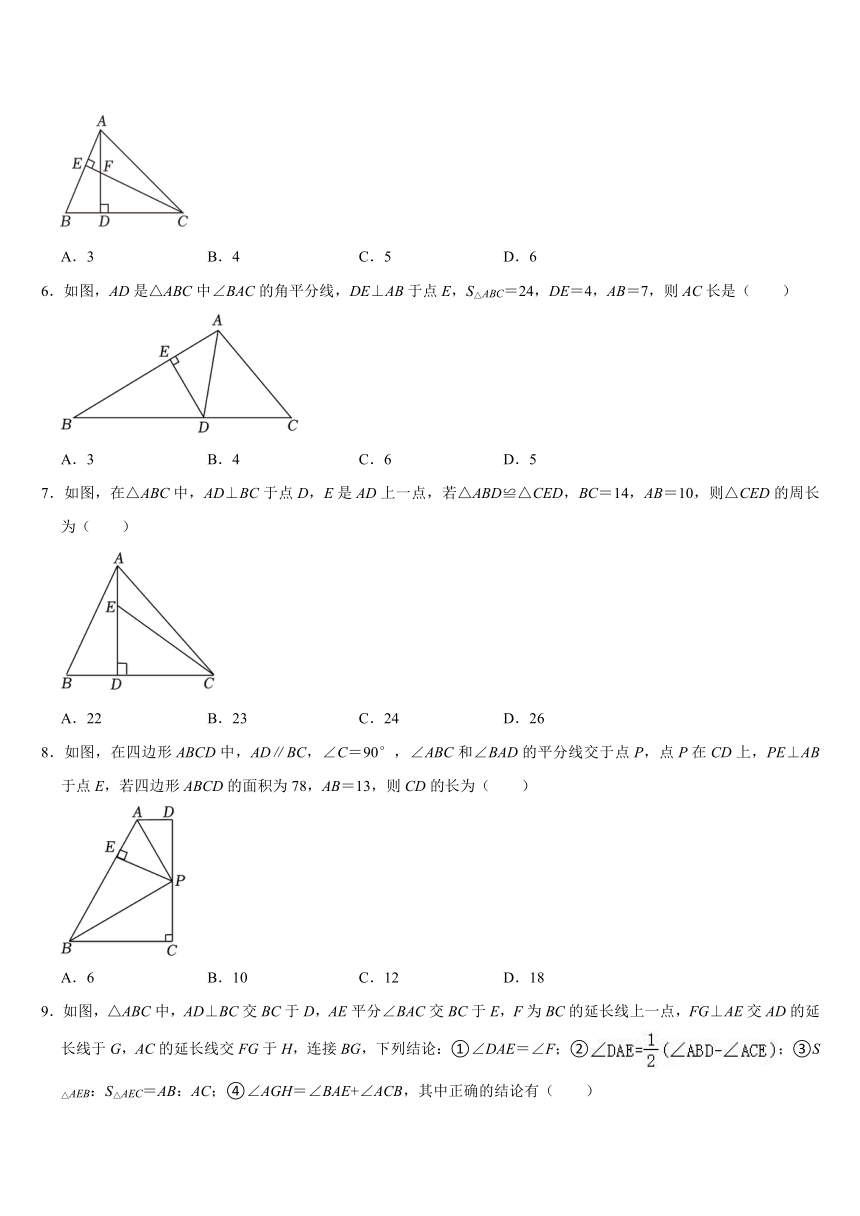
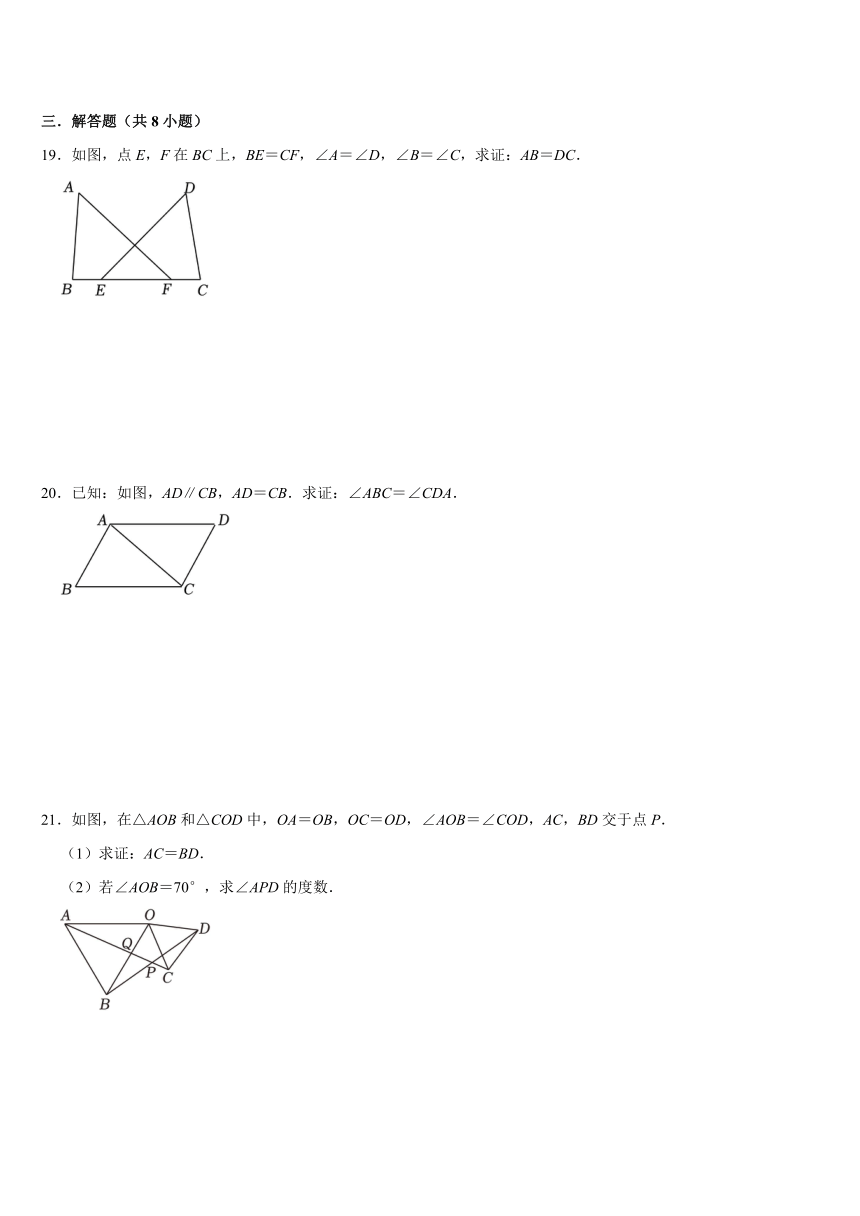
文档简介
人教版数学八年级上第十二章《全等三角形》复习试题
一.选择题(共10小题)
1.下列说法正确的是( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指面积相等的两个三角形
C.有两边和它们的夹角对应相等的两个三角形全等
D.如果两个三角形不全等,那么这两个三角形的面积一定不相等
2.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
3.△ABC与△EDF按如图所示方式放置,点B、F、C、D在同一条直线上,AB∥ED,CD=BF,若要使得△ABC≌△EDF,则需要补充的条件可以是( )
A.∠B=∠E B.AC=EF C.DE=BC D.AB=ED
4.如图,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE为( )
A.20° B.30° C.40° D.50°
5.如图,AD和CE是△ABC的高,交于点F,且BD=FD=4,CD=7,则AF的长为( )
A.3 B.4 C.5 D.6
6.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( )
A.3 B.4 C.6 D.5
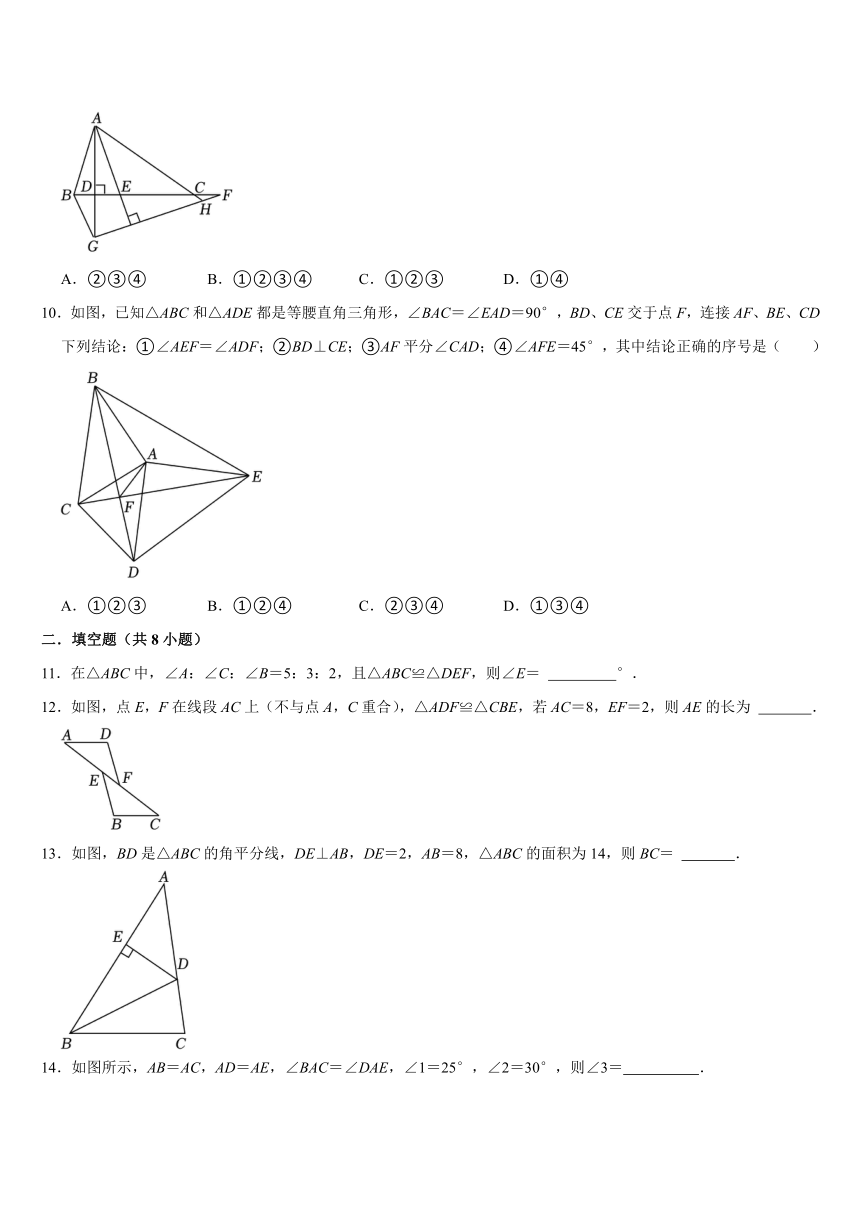
7.如图,在△ABC中,AD⊥BC于点D,E是AD上一点,若△ABD≌△CED,BC=14,AB=10,则△CED的周长为( )
A.22 B.23 C.24 D.26
8.如图,在四边形ABCD中,AD∥BC,∠C=90°,∠ABC和∠BAD的平分线交于点P,点P在CD上,PE⊥AB于点E,若四边形ABCD的面积为78,AB=13,则CD的长为( )
A.6 B.10 C.12 D.18
9.如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DAE=∠F;②;③S△AEB:S△AEC=AB:AC;④∠AGH=∠BAE+∠ACB,其中正确的结论有( )
A.②③④ B.①②③④ C.①②③ D.①④
10.如图,已知△ABC和△ADE都是等腰直角三角形,∠BAC=∠EAD=90°,BD、CE交于点F,连接AF、BE、CD下列结论:①∠AEF=∠ADF;②BD⊥CE;③AF平分∠CAD;④∠AFE=45°,其中结论正确的序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
二.填空题(共8小题)
11.在△ABC中,∠A:∠C:∠B=5:3:2,且△ABC≌△DEF,则∠E= °.
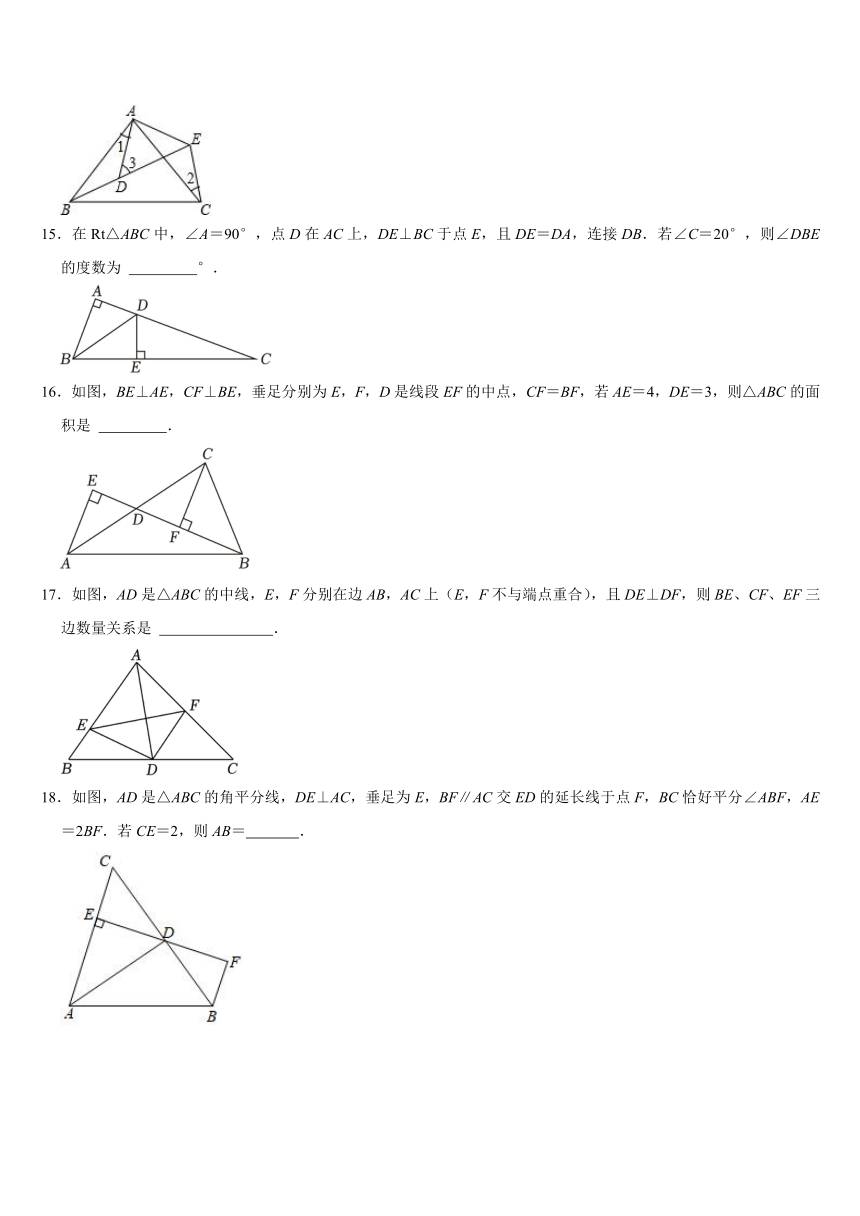
12.如图,点E,F在线段AC上(不与点A,C重合),△ADF≌△CBE,若AC=8,EF=2,则AE的长为 .
13.如图,BD是△ABC的角平分线,DE⊥AB,DE=2,AB=8,△ABC的面积为14,则BC= .
14.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
15.在Rt△ABC中,∠A=90°,点D在AC上,DE⊥BC于点E,且DE=DA,连接DB.若∠C=20°,则∠DBE的度数为 °.
16.如图,BE⊥AE,CF⊥BE,垂足分别为E,F,D是线段EF的中点,CF=BF,若AE=4,DE=3,则△ABC的面积是 .
17.如图,AD是△ABC的中线,E,F分别在边AB,AC上(E,F不与端点重合),且DE⊥DF,则BE、CF、EF三边数量关系是 .
18.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,BC恰好平分∠ABF,AE=2BF.若CE=2,则AB= .
三.解答题(共8小题)
19.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,求证:AB=DC.
20.已知:如图,AD∥CB,AD=CB.求证:∠ABC=∠CDA.
21.如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD,AC,BD交于点P.
(1)求证:AC=BD.
(2)若∠AOB=70°,求∠APD的度数.
22.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
23.如图,已知AB=AC,AD=AE,∠BAC=∠EAD,∠1=25°,∠2=30°.
(1)求证:△ABE≌△ACD;
(2)求∠3的度数.
24.如图,AD是△ABC的中线,BE⊥AD,垂足为E,CF⊥AD,交AD的延长线于点F,G是DA延长线上一点,连接BG.
(1)求证:DE=DF;
(2)若BG=CA,AG=4,求DF的长.
25.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
26.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
参考答案
一.选择题(共10小题)
1.C.
2.B.
3.D.
4.A.
5.A.
6.D.
7.C.
8.C.
9.B.
10.B.
二.填空题(共8小题)
11.36.
12.3.
13.6.
14.55°.
15.35.
16.28.
17.BE+CF>EF.
18.=6,
故答案为:6.
三.解答题(共8小题)
19.证明:∵点E,F在BC上,BE=CF,
∴BE+EF=CF+EF,即BF=CE;
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
∴AB=CD(全等三角形的对应边相等).
20.证明:∵AD∥CB,
∴∠DAC=∠BCA,
在△ADC和△CBA中,
,
∴△ADC≌△CBA(SAS),
∴∠ABC=∠CDA.
21.1)证明:∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC与△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)解:∵△AOC≌△BOD,
∴∠OAC=∠OBD,
∵∠BQP=∠AQO,
∴180°﹣∠AQO﹣∠OAC=180°﹣∠BQP﹣∠OBD,
∴∠AOQ=∠BPQ=70°,
∴∠APD=180°﹣∠BPQ=110°.
22.证明:(1)∵∠1=∠2.
∴∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS);
(2)由第一小问得△ABE≌△CBD,
∴∠A=∠C,
∵∠AFB=∠CFE,
∴∠1=∠3.
23.(1)证明:∵BAC=∠BAE+∠CAE,∠DAE=∠1+∠CAE,∠BAC=∠DAE,
∴∠1=∠BAE,
在△ABE和△ACD中
,
∴△ABE≌△ACD(SAS);
(2)解:∵△ABE≌△ACD,
∴∠2=∠ABD=30°,
∴∠3=∠BAE+∠ABD=∠1+∠ABD=25°+30°=55°.
24.(1)证明:∵AD是△ABC的中线,
∴BD=CD,
∵CF⊥AD,BE⊥AD,
∴∠F=∠BED=90°,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴DE=DF;
(2)解:∵△BDE≌△CDF,
∴BE=CF,
在Rt△BEG和Rt△CFA中,
,
∴Rt△BEG≌Rt△CFA(HL),
∴EG=FA,
∴EG﹣AE=FA﹣AE,
即AG=EF=4,
∵DE=DF,DE+DF=EF,
∴.
25.证明:(1)△DAE≌△CFE理由如下:
∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA);
(2)由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,在△ABE与△FBE中,
,
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,
∴BE⊥AE;
26.:(1)∵BC⊥AE,∠BAE=45°,
∴∠CBA=∠CAB,
∴BC=CA,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BDP=∠ADC,
∴∠BPD=∠DCA=90°,
∵AB=AE,
∴AD平分∠BAE.
(3)AD⊥BE不发生变化.
如图2,
∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BFP=∠AFC,
∴∠BPF=∠ACF=90°,
∴AD⊥BE.
一.选择题(共10小题)
1.下列说法正确的是( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指面积相等的两个三角形
C.有两边和它们的夹角对应相等的两个三角形全等
D.如果两个三角形不全等,那么这两个三角形的面积一定不相等
2.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24 B.27 C.30 D.33
3.△ABC与△EDF按如图所示方式放置,点B、F、C、D在同一条直线上,AB∥ED,CD=BF,若要使得△ABC≌△EDF,则需要补充的条件可以是( )
A.∠B=∠E B.AC=EF C.DE=BC D.AB=ED
4.如图,AD=AE,BE=CD,∠1=∠2=110°,∠BAE=60°,则∠CAE为( )
A.20° B.30° C.40° D.50°
5.如图,AD和CE是△ABC的高,交于点F,且BD=FD=4,CD=7,则AF的长为( )
A.3 B.4 C.5 D.6
6.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( )
A.3 B.4 C.6 D.5
7.如图,在△ABC中,AD⊥BC于点D,E是AD上一点,若△ABD≌△CED,BC=14,AB=10,则△CED的周长为( )
A.22 B.23 C.24 D.26
8.如图,在四边形ABCD中,AD∥BC,∠C=90°,∠ABC和∠BAD的平分线交于点P,点P在CD上,PE⊥AB于点E,若四边形ABCD的面积为78,AB=13,则CD的长为( )
A.6 B.10 C.12 D.18
9.如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DAE=∠F;②;③S△AEB:S△AEC=AB:AC;④∠AGH=∠BAE+∠ACB,其中正确的结论有( )
A.②③④ B.①②③④ C.①②③ D.①④
10.如图,已知△ABC和△ADE都是等腰直角三角形,∠BAC=∠EAD=90°,BD、CE交于点F,连接AF、BE、CD下列结论:①∠AEF=∠ADF;②BD⊥CE;③AF平分∠CAD;④∠AFE=45°,其中结论正确的序号是( )
A.①②③ B.①②④ C.②③④ D.①③④
二.填空题(共8小题)
11.在△ABC中,∠A:∠C:∠B=5:3:2,且△ABC≌△DEF,则∠E= °.
12.如图,点E,F在线段AC上(不与点A,C重合),△ADF≌△CBE,若AC=8,EF=2,则AE的长为 .
13.如图,BD是△ABC的角平分线,DE⊥AB,DE=2,AB=8,△ABC的面积为14,则BC= .
14.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
15.在Rt△ABC中,∠A=90°,点D在AC上,DE⊥BC于点E,且DE=DA,连接DB.若∠C=20°,则∠DBE的度数为 °.
16.如图,BE⊥AE,CF⊥BE,垂足分别为E,F,D是线段EF的中点,CF=BF,若AE=4,DE=3,则△ABC的面积是 .
17.如图,AD是△ABC的中线,E,F分别在边AB,AC上(E,F不与端点重合),且DE⊥DF,则BE、CF、EF三边数量关系是 .
18.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,BC恰好平分∠ABF,AE=2BF.若CE=2,则AB= .
三.解答题(共8小题)
19.如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,求证:AB=DC.
20.已知:如图,AD∥CB,AD=CB.求证:∠ABC=∠CDA.
21.如图,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD,AC,BD交于点P.
(1)求证:AC=BD.
(2)若∠AOB=70°,求∠APD的度数.
22.如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
23.如图,已知AB=AC,AD=AE,∠BAC=∠EAD,∠1=25°,∠2=30°.
(1)求证:△ABE≌△ACD;
(2)求∠3的度数.
24.如图,AD是△ABC的中线,BE⊥AD,垂足为E,CF⊥AD,交AD的延长线于点F,G是DA延长线上一点,连接BG.
(1)求证:DE=DF;
(2)若BG=CA,AG=4,求DF的长.
25.如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)求证:△DAE≌△CFE;
(2)若AB=BC+AD,求证:BE⊥AF.
26.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;
(1)求证:AD=BE;
(2)试说明AD平分∠BAE;
(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.
参考答案
一.选择题(共10小题)
1.C.
2.B.
3.D.
4.A.
5.A.
6.D.
7.C.
8.C.
9.B.
10.B.
二.填空题(共8小题)
11.36.
12.3.
13.6.
14.55°.
15.35.
16.28.
17.BE+CF>EF.
18.=6,
故答案为:6.
三.解答题(共8小题)
19.证明:∵点E,F在BC上,BE=CF,
∴BE+EF=CF+EF,即BF=CE;
在△ABF和△DCE中,
,
∴△ABF≌△DCE(AAS),
∴AB=CD(全等三角形的对应边相等).
20.证明:∵AD∥CB,
∴∠DAC=∠BCA,
在△ADC和△CBA中,
,
∴△ADC≌△CBA(SAS),
∴∠ABC=∠CDA.
21.1)证明:∵∠AOB=∠COD,
∴∠AOB+∠BOC=∠COD+∠BOC,
即∠AOC=∠BOD,
在△AOC与△BOD中,
,
∴△AOC≌△BOD(SAS),
∴AC=BD;
(2)解:∵△AOC≌△BOD,
∴∠OAC=∠OBD,
∵∠BQP=∠AQO,
∴180°﹣∠AQO﹣∠OAC=180°﹣∠BQP﹣∠OBD,
∴∠AOQ=∠BPQ=70°,
∴∠APD=180°﹣∠BPQ=110°.
22.证明:(1)∵∠1=∠2.
∴∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS);
(2)由第一小问得△ABE≌△CBD,
∴∠A=∠C,
∵∠AFB=∠CFE,
∴∠1=∠3.
23.(1)证明:∵BAC=∠BAE+∠CAE,∠DAE=∠1+∠CAE,∠BAC=∠DAE,
∴∠1=∠BAE,
在△ABE和△ACD中
,
∴△ABE≌△ACD(SAS);
(2)解:∵△ABE≌△ACD,
∴∠2=∠ABD=30°,
∴∠3=∠BAE+∠ABD=∠1+∠ABD=25°+30°=55°.
24.(1)证明:∵AD是△ABC的中线,
∴BD=CD,
∵CF⊥AD,BE⊥AD,
∴∠F=∠BED=90°,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(AAS),
∴DE=DF;
(2)解:∵△BDE≌△CDF,
∴BE=CF,
在Rt△BEG和Rt△CFA中,
,
∴Rt△BEG≌Rt△CFA(HL),
∴EG=FA,
∴EG﹣AE=FA﹣AE,
即AG=EF=4,
∵DE=DF,DE+DF=EF,
∴.
25.证明:(1)△DAE≌△CFE理由如下:
∵AD∥BC(已知),
∴∠ADC=∠ECF(两直线平行,内错角相等),
∵E是CD的中点(已知),
∴DE=EC(中点的定义).
∵在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA);
(2)由(1)知△ADE≌△FCE,
∴AE=EF,AD=CF,
∵AB=BC+AD,
∴AB=BC+CF,
即AB=BF,在△ABE与△FBE中,
,
∴△ABE≌△FBE(SSS),
∴∠AEB=∠FEB=90°,
∴BE⊥AE;
26.:(1)∵BC⊥AE,∠BAE=45°,
∴∠CBA=∠CAB,
∴BC=CA,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BDP=∠ADC,
∴∠BPD=∠DCA=90°,
∵AB=AE,
∴AD平分∠BAE.
(3)AD⊥BE不发生变化.
如图2,
∵△BCE≌△ACD,
∴∠EBC=∠DAC,
∵∠BFP=∠AFC,
∴∠BPF=∠ACF=90°,
∴AD⊥BE.
