第十二章 全等三角形 复习试题(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第十二章 全等三角形 复习试题(含答案) 2024—2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 265.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览



文档简介
人教版数学八年级上第十二章《全等三角形》复习试题
一.选择题(共10小题)
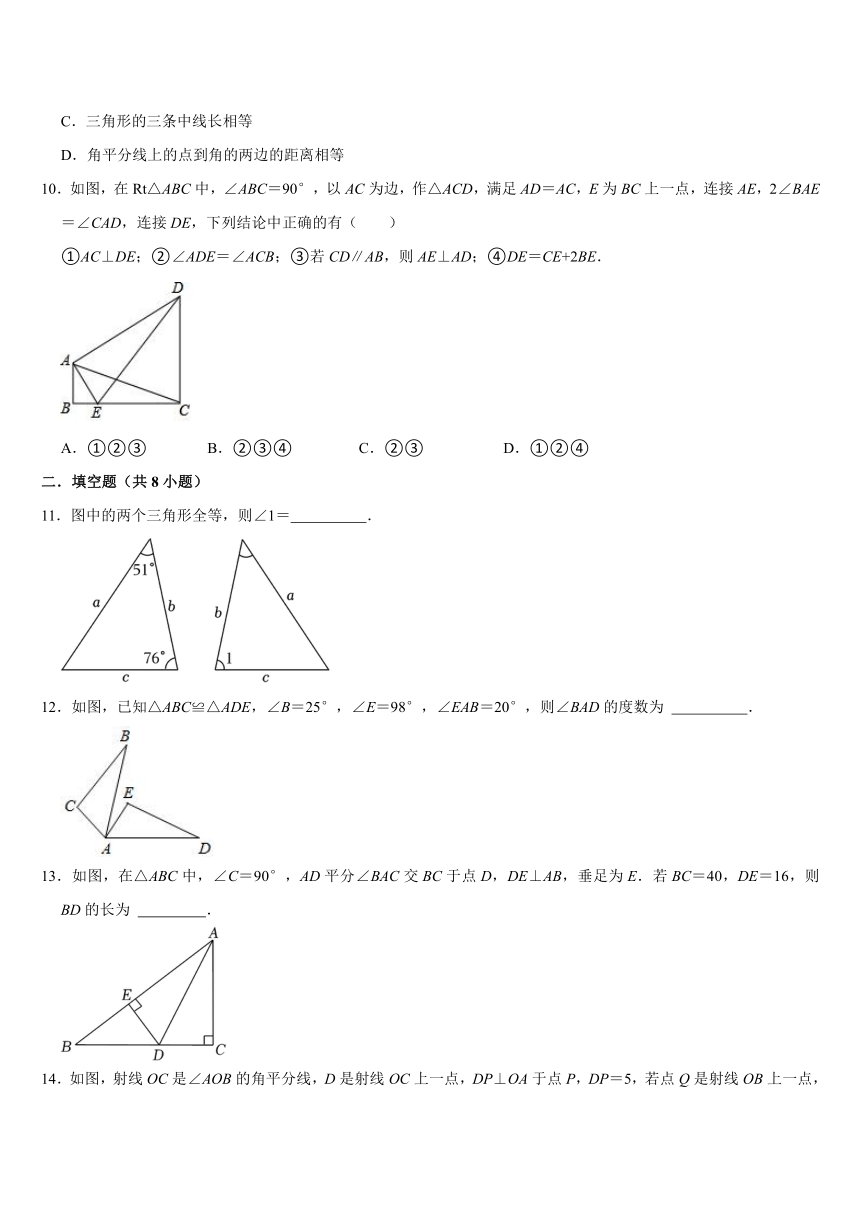
1.如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论错误的是( )
A.AC⊥BD B.BC=CD C.△ABC≌△ADC D.DA=DC
2.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且BC=5cm,BD=3cm,则DE等于( )
A.2cm B.3cm C.4cm D.5cm
3.如图,若∠C=∠D,∠1=∠2,则直接判定△ABC≌△ABD的理由是( )
A.SAS B.SSS C.ASA D.AAS
4.如图,已知OB=OA,OD=OC,∠O=65°,∠C=20°,则∠AEB的度数为( )
A.90° B.115° C.95° D.105°
5.如图,△ABC中,∠B=2∠A,∠ACB的平分线CD交AB于点D,已知AC=16,BC=9,则BD的长为( )
A.6 B.7 C.8 D.9
6.如图,在△ABC中,AD是∠BAC的平分线,DF⊥AB,垂足为F,DE=DG,若△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.8 B.12 C.4 D.6
7.如图,△ABC≌△DEC,点A,E,C在同一直线上,AE=3,CD=8,则BC的长为( )
A.3 B.5 C.6 D.8
8.如图,在四边形ABCD中,AB∥CD,∠C=90°,若∠DAB的角平分线AE交BC于E,连接DE,且DE边平分∠ADC,则以下命题正确的个数是( )
①CD+AB=BC;②E为BC中点;③∠AED=90°;④S△ADE=S四边形ABCD.
A.1个 B.2个 C.3个 D.4个
9.下列说法正确的是( )
A.三角形的一个外角大于它的任何一个内角
B.钝角三角形的三个内角都是钝角
C.三角形的三条中线长相等
D.角平分线上的点到角的两边的距离相等
10.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE,下列结论中正确的有( )
①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB,则AE⊥AD;④DE=CE+2BE.
A.①②③ B.②③④ C.②③ D.①②④
二.填空题(共8小题)
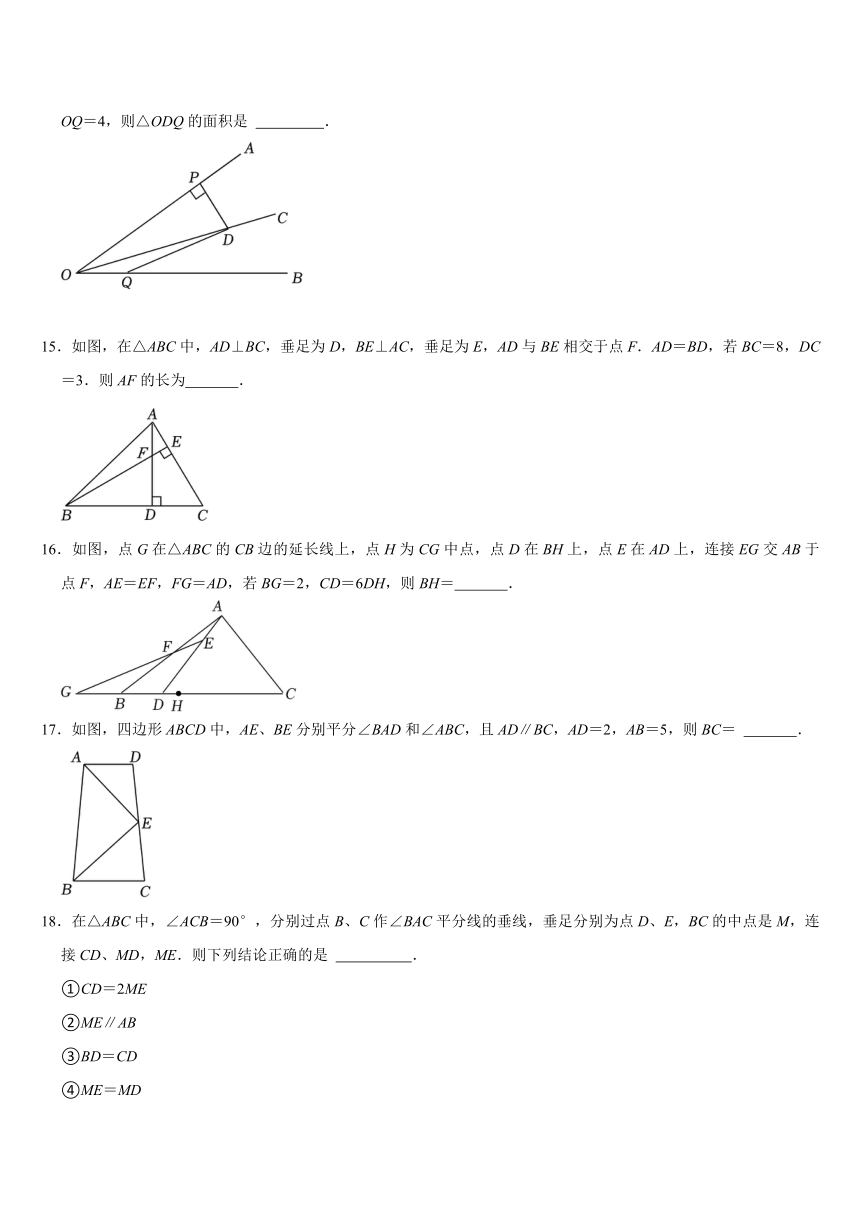
11.图中的两个三角形全等,则∠1= .
12.如图,已知△ABC≌△ADE,∠B=25°,∠E=98°,∠EAB=20°,则∠BAD的度数为 .
13.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若BC=40,DE=16,则BD的长为 .
14.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 .
15.如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F.AD=BD,若BC=8,DC=3.则AF的长为 .
16.如图,点G在△ABC的CB边的延长线上,点H为CG中点,点D在BH上,点E在AD上,连接EG交AB于点F,AE=EF,FG=AD,若BG=2,CD=6DH,则BH= .
17.如图,四边形ABCD中,AE、BE分别平分∠BAD和∠ABC,且AD∥BC,AD=2,AB=5,则BC= .
18.在△ABC中,∠ACB=90°,分别过点B、C作∠BAC平分线的垂线,垂足分别为点D、E,BC的中点是M,连接CD、MD,ME.则下列结论正确的是 .
①CD=2ME
②ME∥AB
③BD=CD
④ME=MD
三.解答题(共8小题)
19.如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,求证:OD=ON+DM.
20.在△ABC中,AB=AC,点D是直线BC上一点(点D不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)求证:△ABD≌△ACE;
(2)∠BCE和∠BAC之间有怎样的数量关系?说明理由.
21.如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
22.在△ABC中,点D,E,F分别是边BC,AB,AC上的点,DE⊥BA,BC⊥AC,已知BD=DF,BE=FC.证明:AD是∠BAC的平分线.
23.如图,在△ABC中,D为BC的中点,E是AD上一点,连接BE并延长交AC于点F,BE=AC,且BF=9,CF=6,求AF的长.
24.如图,已知:A、F、C、D在同一条直线上,BC=EF,AB=DE,AC=FD.求证:(1)BC∥EF;
(2)CE=BF.
25.锐角△ABC中,BE,CF是高,在BE,CF或它们的延长线上分别截取BQ=CA,CP=BA,作PP′⊥BC 于P′,QQ′⊥BC于Q′.求证:PP′+QQ′=BC.
26.如图,已知在△ABC中,BD⊥AC于点D,CE⊥AB于点E,F是线段BD上一点,BF=AC,G是线段CE延长线上一点,CG=AB,连接AG、AF.
(1)试说明:∠ABD=∠ACE;
(2)试猜想线段AF与AG之间的关系,并说明理由.
参考答案
一.选择题(共10小题)
1.D.
2.A.
3.D.
4.D.
5.B.
6.D.
7.B.
8.C.
9.D.
10.B.
二.填空题(共8小题)
11.76°.
12.77°.
13.24.
14.10.
15.2.
16.3.
17.3.
18.②③④.
三.解答题(共8小题)
19.证明:∵OC是∠AOB的平分线,
∴∠DOC=∠COB,
又∵CD∥OB,
∴∠DOC=∠DCO,
∴OD=CD=DM+CM,
∵E是线段OC的中点,
∴CE=OE,
在△MEC与△NEO中
,
∴△MEC≌△NEO
∴CM=ON,
∴OD=ON+DM.
20.(1)证明:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∠BCE+∠BAC=180°.
理由:∵△ABD≌△ACE,
∴∠B=∠ACE,
∵∠BCE=∠ACE+∠ACB,
∴∠BCE=∠B+∠ACB,
∵∠B+∠ACB+∠BAC=180°,
∴∠BAC+∠BCE=180°.
21.证明:∵∠1=∠2,
∴∠1+∠EAB=∠2+∠EAB,
∴∠DAB=∠CAE,
在△DAB和△EAC中
∴△DAB≌△EAC(SAS),
∴∠B=∠C.
22.证明:∵DE⊥BA,BC⊥AC,
∴∠BED=∠C=90°,
在Rt△BED和Rt△FCD中,
,
∴Rt△BED≌Rt△FCD(HL),
∴DE=DC,
∵DE⊥BA,BC⊥AC,
∴AD是∠BAC的平分线.
23.解:如图,延长AD至H,使DH=DE,
∵AD为中线,
∴BD=CD,
∵∠EDB=∠HDC,
∴△BDE≌△CDH(SAS),
∴CH=BE,
∵BE=AC,
∴CH=AC,
∴∠H=∠EAF,
∵△BDE≌△CDH,
∴∠H=∠AED=∠AEF,
∴∠AEF=∠EAF,
∴AF=EF,
设AF=x,
∴AC=6+x,BE=9﹣x,
∵BE=AC,即6+x=9﹣x,
∴x=,即AF=.
24.证明:(1)在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠BCA=∠EFD,
∴BC∥EF.
(2)∵△ABC≌△DEF,
∴∠A=∠D,
∵AC=DF,
∴AC﹣CF=DF﹣CF,
∴AF=DC,
∵AB=DE,
∴△ABF≌△DEC(SAS),
∴BF=CE.
25.证明:作AM⊥BC于M.
∵AM⊥BC,CF⊥AB,
∴∠BAM+∠ABC=90°,∠FCB+∠ABC=90°,
∴∠BAM=∠FCB.
∵∠PP′C=∠AMB=90°,∠BAM=∠FCB,AB=CP,
∴△ABM≌△CPP′(AAS).
∴BM=PP′.
∵QQ′⊥BC,BE⊥AC,
∴∠QBC+∠ACB=90°,∠BQQ′+∠QBC=90°,
∴∠ACB=∠BQQ′,
∵∠ACB=∠BQQ′,∠AMC=∠BQQ′=90°,AC=BQ,
∴△AMC≌△BQQ′(AAS),
∴QQ′=MC.
∵QQ′=MC,PP′=MB,MC+MB=BC,
∴PP′+QQ′=BC.
26.(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°,∠GCA+∠BAD=90°,
∴∠ABD=∠ACE.
(2)结论:AF=AG,AF⊥AG.理由如下:
在△ABF和△GCA中,AB=CG,∠ABF=∠GCA,BF=AC,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠GAC=∠AFB.
∵∠AFB=∠ADB+∠FAD,∠GAC=∠GAF+∠FAD,
∴∠GAF=∠ADF.
∵∠ADF=90°,
∴∠GAF=90°,
∴AG⊥AF,AG=AF.
一.选择题(共10小题)
1.如图,四边形ABCD的对角线AC、BD相交于点O,△ABO≌△ADO,下列结论错误的是( )
A.AC⊥BD B.BC=CD C.△ABC≌△ADC D.DA=DC
2.如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB于E,且BC=5cm,BD=3cm,则DE等于( )
A.2cm B.3cm C.4cm D.5cm
3.如图,若∠C=∠D,∠1=∠2,则直接判定△ABC≌△ABD的理由是( )
A.SAS B.SSS C.ASA D.AAS
4.如图,已知OB=OA,OD=OC,∠O=65°,∠C=20°,则∠AEB的度数为( )
A.90° B.115° C.95° D.105°
5.如图,△ABC中,∠B=2∠A,∠ACB的平分线CD交AB于点D,已知AC=16,BC=9,则BD的长为( )
A.6 B.7 C.8 D.9
6.如图,在△ABC中,AD是∠BAC的平分线,DF⊥AB,垂足为F,DE=DG,若△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.8 B.12 C.4 D.6
7.如图,△ABC≌△DEC,点A,E,C在同一直线上,AE=3,CD=8,则BC的长为( )
A.3 B.5 C.6 D.8
8.如图,在四边形ABCD中,AB∥CD,∠C=90°,若∠DAB的角平分线AE交BC于E,连接DE,且DE边平分∠ADC,则以下命题正确的个数是( )
①CD+AB=BC;②E为BC中点;③∠AED=90°;④S△ADE=S四边形ABCD.
A.1个 B.2个 C.3个 D.4个
9.下列说法正确的是( )
A.三角形的一个外角大于它的任何一个内角
B.钝角三角形的三个内角都是钝角
C.三角形的三条中线长相等
D.角平分线上的点到角的两边的距离相等
10.如图,在Rt△ABC中,∠ABC=90°,以AC为边,作△ACD,满足AD=AC,E为BC上一点,连接AE,2∠BAE=∠CAD,连接DE,下列结论中正确的有( )
①AC⊥DE;②∠ADE=∠ACB;③若CD∥AB,则AE⊥AD;④DE=CE+2BE.
A.①②③ B.②③④ C.②③ D.①②④
二.填空题(共8小题)
11.图中的两个三角形全等,则∠1= .
12.如图,已知△ABC≌△ADE,∠B=25°,∠E=98°,∠EAB=20°,则∠BAD的度数为 .
13.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E.若BC=40,DE=16,则BD的长为 .
14.如图,射线OC是∠AOB的角平分线,D是射线OC上一点,DP⊥OA于点P,DP=5,若点Q是射线OB上一点,OQ=4,则△ODQ的面积是 .
15.如图,在△ABC中,AD⊥BC,垂足为D,BE⊥AC,垂足为E,AD与BE相交于点F.AD=BD,若BC=8,DC=3.则AF的长为 .
16.如图,点G在△ABC的CB边的延长线上,点H为CG中点,点D在BH上,点E在AD上,连接EG交AB于点F,AE=EF,FG=AD,若BG=2,CD=6DH,则BH= .
17.如图,四边形ABCD中,AE、BE分别平分∠BAD和∠ABC,且AD∥BC,AD=2,AB=5,则BC= .
18.在△ABC中,∠ACB=90°,分别过点B、C作∠BAC平分线的垂线,垂足分别为点D、E,BC的中点是M,连接CD、MD,ME.则下列结论正确的是 .
①CD=2ME
②ME∥AB
③BD=CD
④ME=MD
三.解答题(共8小题)
19.如图,过∠AOB平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,请过点E画直线分别交射线CD、OB于点M、N,求证:OD=ON+DM.
20.在△ABC中,AB=AC,点D是直线BC上一点(点D不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)求证:△ABD≌△ACE;
(2)∠BCE和∠BAC之间有怎样的数量关系?说明理由.
21.如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
22.在△ABC中,点D,E,F分别是边BC,AB,AC上的点,DE⊥BA,BC⊥AC,已知BD=DF,BE=FC.证明:AD是∠BAC的平分线.
23.如图,在△ABC中,D为BC的中点,E是AD上一点,连接BE并延长交AC于点F,BE=AC,且BF=9,CF=6,求AF的长.
24.如图,已知:A、F、C、D在同一条直线上,BC=EF,AB=DE,AC=FD.求证:(1)BC∥EF;
(2)CE=BF.
25.锐角△ABC中,BE,CF是高,在BE,CF或它们的延长线上分别截取BQ=CA,CP=BA,作PP′⊥BC 于P′,QQ′⊥BC于Q′.求证:PP′+QQ′=BC.
26.如图,已知在△ABC中,BD⊥AC于点D,CE⊥AB于点E,F是线段BD上一点,BF=AC,G是线段CE延长线上一点,CG=AB,连接AG、AF.
(1)试说明:∠ABD=∠ACE;
(2)试猜想线段AF与AG之间的关系,并说明理由.
参考答案
一.选择题(共10小题)
1.D.
2.A.
3.D.
4.D.
5.B.
6.D.
7.B.
8.C.
9.D.
10.B.
二.填空题(共8小题)
11.76°.
12.77°.
13.24.
14.10.
15.2.
16.3.
17.3.
18.②③④.
三.解答题(共8小题)
19.证明:∵OC是∠AOB的平分线,
∴∠DOC=∠COB,
又∵CD∥OB,
∴∠DOC=∠DCO,
∴OD=CD=DM+CM,
∵E是线段OC的中点,
∴CE=OE,
在△MEC与△NEO中
,
∴△MEC≌△NEO
∴CM=ON,
∴OD=ON+DM.
20.(1)证明:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∠BCE+∠BAC=180°.
理由:∵△ABD≌△ACE,
∴∠B=∠ACE,
∵∠BCE=∠ACE+∠ACB,
∴∠BCE=∠B+∠ACB,
∵∠B+∠ACB+∠BAC=180°,
∴∠BAC+∠BCE=180°.
21.证明:∵∠1=∠2,
∴∠1+∠EAB=∠2+∠EAB,
∴∠DAB=∠CAE,
在△DAB和△EAC中
∴△DAB≌△EAC(SAS),
∴∠B=∠C.
22.证明:∵DE⊥BA,BC⊥AC,
∴∠BED=∠C=90°,
在Rt△BED和Rt△FCD中,
,
∴Rt△BED≌Rt△FCD(HL),
∴DE=DC,
∵DE⊥BA,BC⊥AC,
∴AD是∠BAC的平分线.
23.解:如图,延长AD至H,使DH=DE,
∵AD为中线,
∴BD=CD,
∵∠EDB=∠HDC,
∴△BDE≌△CDH(SAS),
∴CH=BE,
∵BE=AC,
∴CH=AC,
∴∠H=∠EAF,
∵△BDE≌△CDH,
∴∠H=∠AED=∠AEF,
∴∠AEF=∠EAF,
∴AF=EF,
设AF=x,
∴AC=6+x,BE=9﹣x,
∵BE=AC,即6+x=9﹣x,
∴x=,即AF=.
24.证明:(1)在△ABC与△DEF中,
,
∴△ABC≌△DEF(SSS),
∴∠BCA=∠EFD,
∴BC∥EF.
(2)∵△ABC≌△DEF,
∴∠A=∠D,
∵AC=DF,
∴AC﹣CF=DF﹣CF,
∴AF=DC,
∵AB=DE,
∴△ABF≌△DEC(SAS),
∴BF=CE.
25.证明:作AM⊥BC于M.
∵AM⊥BC,CF⊥AB,
∴∠BAM+∠ABC=90°,∠FCB+∠ABC=90°,
∴∠BAM=∠FCB.
∵∠PP′C=∠AMB=90°,∠BAM=∠FCB,AB=CP,
∴△ABM≌△CPP′(AAS).
∴BM=PP′.
∵QQ′⊥BC,BE⊥AC,
∴∠QBC+∠ACB=90°,∠BQQ′+∠QBC=90°,
∴∠ACB=∠BQQ′,
∵∠ACB=∠BQQ′,∠AMC=∠BQQ′=90°,AC=BQ,
∴△AMC≌△BQQ′(AAS),
∴QQ′=MC.
∵QQ′=MC,PP′=MB,MC+MB=BC,
∴PP′+QQ′=BC.
26.(1)证明:∵BD、CE是△ABC的高,
∴∠ADB=∠AEC=90°,
∴∠ABF+∠BAD=90°,∠GCA+∠BAD=90°,
∴∠ABD=∠ACE.
(2)结论:AF=AG,AF⊥AG.理由如下:
在△ABF和△GCA中,AB=CG,∠ABF=∠GCA,BF=AC,
∴△ABF≌△GCA(SAS),
∴AF=AG,∠GAC=∠AFB.
∵∠AFB=∠ADB+∠FAD,∠GAC=∠GAF+∠FAD,
∴∠GAF=∠ADF.
∵∠ADF=90°,
∴∠GAF=90°,
∴AG⊥AF,AG=AF.
