第十一章 三角形 复习试题(含答案) 2024--2025学年人教版八年级数学上册
文档属性
| 名称 | 第十一章 三角形 复习试题(含答案) 2024--2025学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 407.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 18:52:18 | ||
图片预览


文档简介
人教版数学八年级上第十一章《三角形》复习试题
一.选择题(共10小题)
1.一个多边形的内角和是1260°,则这个多边形是( )
A.十边形 B.九边形 C.八边形 D.七边形
2.下列长度的各组线段中,能组成三角形的是( )
A.2,3,5 B.3,3,6 C.3,4,5 D.5,6,12
3.如图,在△ABC中,点E是BC的中点,AB=7,AC=10,△ACE的周长是25,则△ABE的周长是( )
A.18 B.22 C.28 D.32
4.画△ABC的边AC边的高,正确的是( )
A.B. C.D.
5.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
6.下列说法中,正确的是( )
A.三角形的三条高都在三角形内,且都相交于一点
B.三角形的一个外角大于任何一个内角
C.任意三角形的外角和都是360°
D.△ABC中,当,时,这个三角形是直角三角形
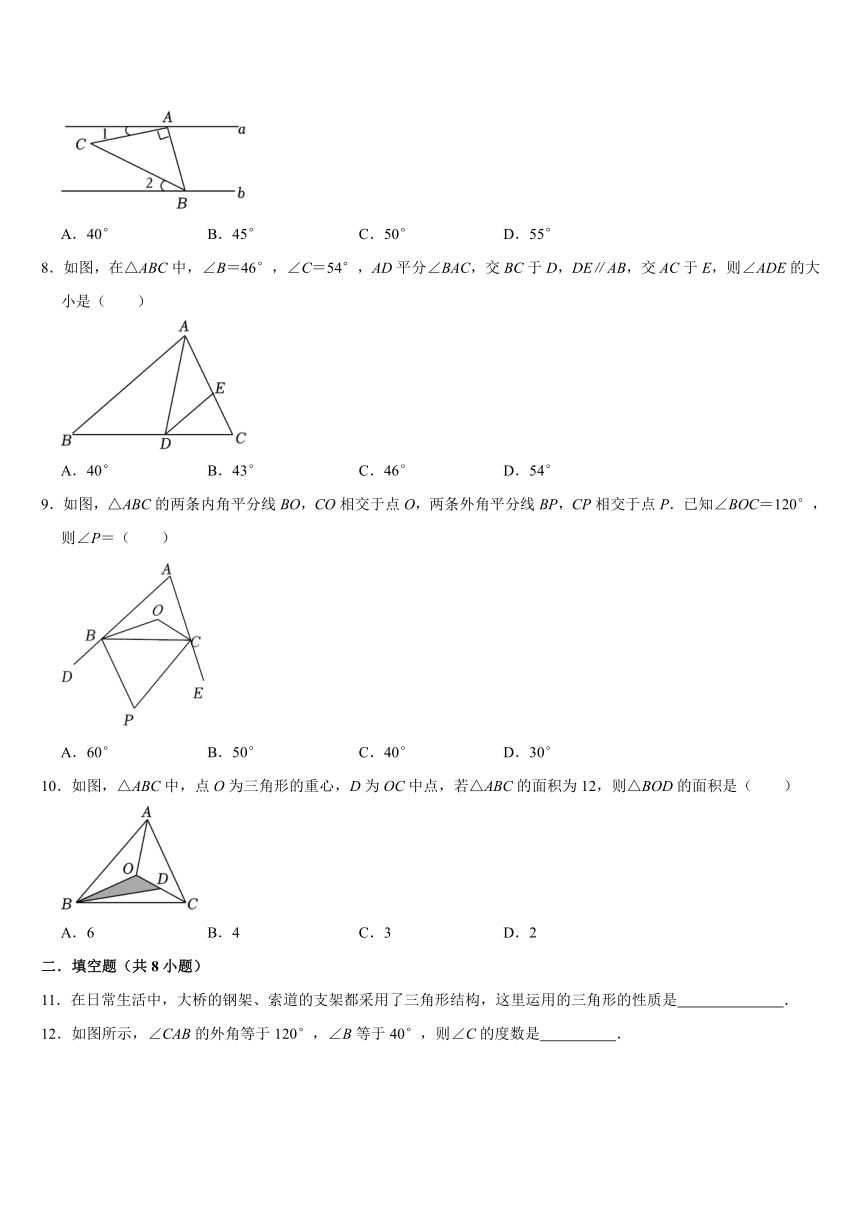
7.如图,直线a∥b,Rt△ABC的直角顶点A落在直线a上,点B落在直线b上,若∠1=15°,∠2=25°,则∠ABC的大小为( )
A.40° B.45° C.50° D.55°
8.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
A.40° B.43° C.46° D.54°
9.如图,△ABC的两条内角平分线BO,CO相交于点O,两条外角平分线BP,CP相交于点P.已知∠BOC=120°,则∠P=( )
A.60° B.50° C.40° D.30°
10.如图,△ABC中,点O为三角形的重心,D为OC中点,若△ABC的面积为12,则△BOD的面积是( )
A.6 B.4 C.3 D.2
二.填空题(共8小题)
11.在日常生活中,大桥的钢架、索道的支架都采用了三角形结构,这里运用的三角形的性质是 .
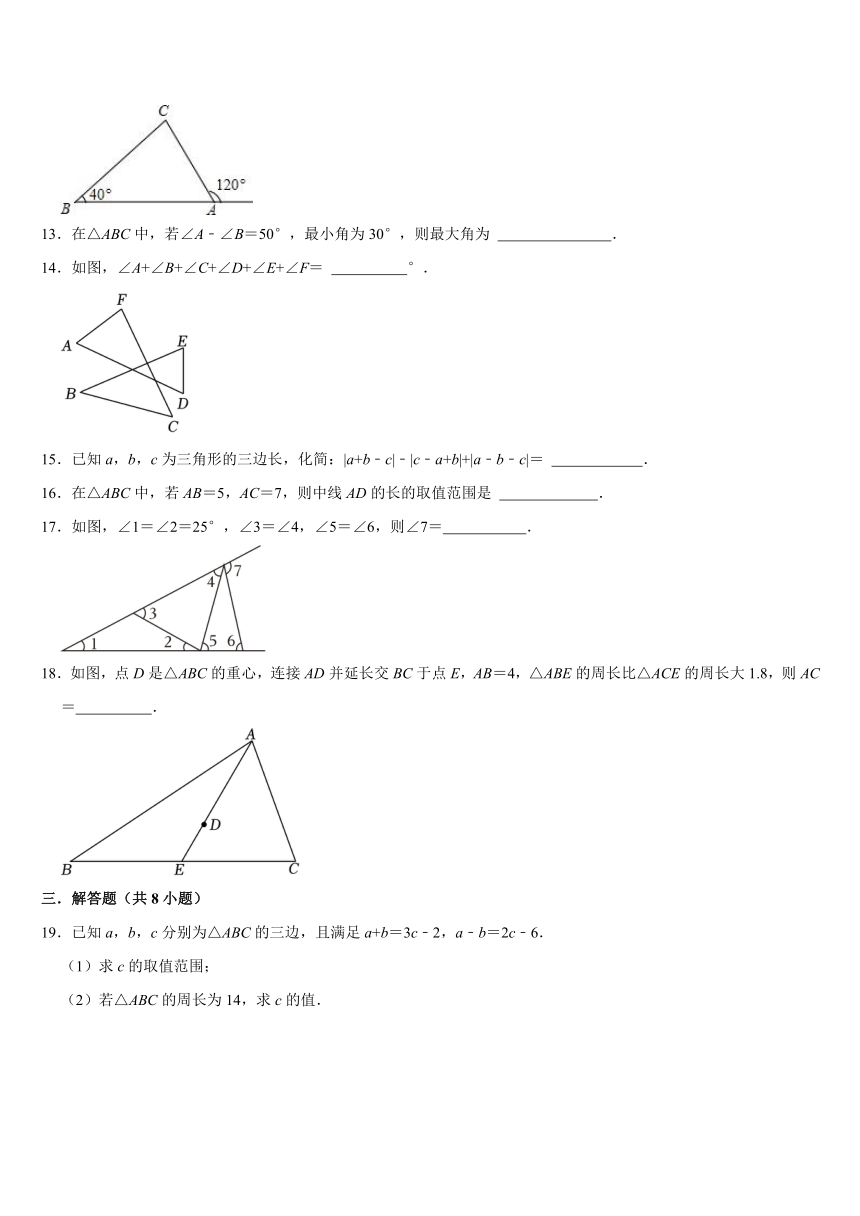
12.如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是 .
13.在△ABC中,若∠A﹣∠B=50°,最小角为30°,则最大角为 .
14.如图,∠A+∠B+∠C+∠D+∠E+∠F= °.
15.已知a,b,c为三角形的三边长,化简:|a+b﹣c|﹣|c﹣a+b|+|a﹣b﹣c|= .
16.在△ABC中,若AB=5,AC=7,则中线AD的长的取值范围是 .
17.如图,∠1=∠2=25°,∠3=∠4,∠5=∠6,则∠7= .
18.如图,点D是△ABC的重心,连接AD并延长交BC于点E,AB=4,△ABE的周长比△ACE的周长大1.8,则AC= .
三.解答题(共8小题)
19.已知a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6.
(1)求c的取值范围;
(2)若△ABC的周长为14,求c的值.
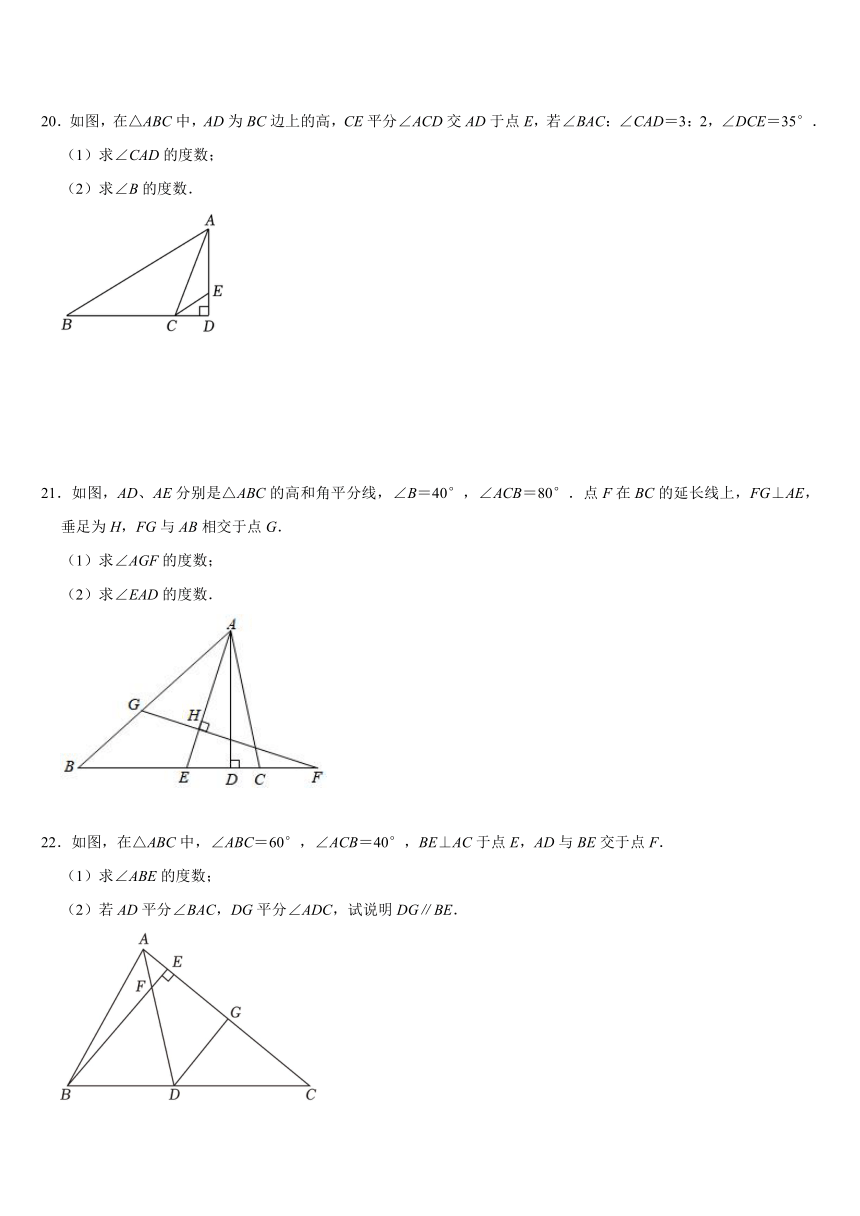
20.如图,在△ABC中,AD为BC边上的高,CE平分∠ACD交AD于点E,若∠BAC:∠CAD=3:2,∠DCE=35°.
(1)求∠CAD的度数;
(2)求∠B的度数.
21.如图,AD、AE分别是△ABC的高和角平分线,∠B=40°,∠ACB=80°.点F在BC的延长线上,FG⊥AE,垂足为H,FG与AB相交于点G.
(1)求∠AGF的度数;
(2)求∠EAD的度数.
22.如图,在△ABC中,∠ABC=60°,∠ACB=40°,BE⊥AC于点E,AD与BE交于点F.
(1)求∠ABE的度数;
(2)若AD平分∠BAC,DG平分∠ADC,试说明DG∥BE.
23.如图1,像我们常见的学习用品——圆规,我们把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块直角三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=54°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=α,∠DBE=β,请用含α和β的式子表示∠DCE的度数.
24.下面是有关三角形内角、外角平分线的探究,阅读后请按要求作答:
(1)如图1,BE、CE分别是∠ABC和∠ACB的平分线且相交于点E,若∠A=30°,则∠E= ;
(2)如图2,BE平分∠ABC,CE平分∠ACD,BE和CE交于点E,猜想∠A与∠E之间的数量关系,并说明理由;
(3)如图3,BE,CE分别是△ABC外角∠CBD和∠BCF的平分线且相交于点E,直接写出∠A与∠E之间的数量关系.
25.定义:在一个三角形中,如果有一个角是另一个角的,我们称这两个角互为“友爱角”,这个三角形叫作“友爱三角形”.例如:在△ABC中,如果∠A=80°,∠B=40°,那么∠A与∠B互为“友爱角”,△ABC为“友爱三角形”.
(1)如图1,△ABC是“友爱三角形”,且∠A与∠B互为“友爱角”(∠A>∠B),∠ACB=90°.
①求∠A、∠B的度数.
②若CD是△ABC中AB边上的高,则△ACD、△BCD都是“友爱三角形”吗?为什么?
(2)如图2,在△ABC中,∠ACB=70°,∠A=66°,D是边AB上一点(不与点A,B重合),连接CD,若△ACD是“友爱三角形”,直接写出∠ACD的度数.
26.点D为∠BAC内一点,连接BD,CD,∠B>∠C,0°<∠BDC≤180°,∠BAC,∠BDC的平分线交于点E.
(1)如图1,当B,D,C三点共线时,若∠ABD=70°,∠ACD=40°,直接写出∠AED的度数是 ;
(2)如图2,若∠B=50°,∠C=20°,求∠AED;
(3)直接写出∠B,∠C,∠AED之间的数量关系是 .
参考答案
一.选择题(共10小题)
1.B.
2.C.
3.B.
4.D.
5.A.
6.C.
7.C.
8.A.
9.A.
10.D.
二.填空题(共8小题)
11.三角形的稳定性.
12.80°.
13.100°或80°.
14.360.
15.a+b﹣c.
16.1<AD<6.
17.100°.
18.2.2.
三.解答题(共8小题)
19.解:(1)∵a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6,
∴a+b=3c﹣2>c,a﹣b=2c﹣6<c,
∴,
解得,1<c<6,
∴c的取值范围为1<c<6;
(2)由题意知,a+b+c=3c﹣2+c=14,
解得,c=4,
∴c的值为4.
20.解:(1)∵CE平分∠ACD,
∴∠DCA=2∠DCE,
∵∠DCE=35°,
∴∠DCA=2∠DCE=2×35°=70°,
∵AD为BC边上的高,
∴∠ADB=90°,
∴∠CAD=90°﹣∠DCA=20°;
(2)∵∠BAC:∠CAD=3:2,∠CAD=20°,
∴∠BAC=30°,
∴∠BAD=∠BAC+∠CAD=20°+30°=50°,
∴∠B=90°﹣∠BAD=90°﹣50°=40°.
21.解:(1)∵∠B=40°,∠ACB=80°,
∴∠BAC=180°﹣40°﹣80°=60°,
∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=30°,
∵FG⊥AE,
∴∠AHG=90°,
∴∠AGF=180°﹣90°﹣30°=60°;
(2)∵AD是△ABC的高,
∴∠ADC=90°,
∵∠ACB=80°,
∴∠CAD=180°﹣90°﹣80°=10°,
∵∠BAC=60°,AE是△ABC的角平分线,
∴∠CAE=∠BAC=30°,
∴∠EAD=∠CAE﹣∠CAD=30°﹣10°=20°.
22.解:(1)∵∠ABC+∠BAC+∠ACB=180°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣40°=80°.
∵AC⊥BE,
∴∠AEB=90°,
∴∠ABE=90°﹣∠BAC=90°﹣80°=10°.
(2)∵AD平分∠BAC,
∴,
∴∠ADC=∠ABC+∠BAD=60°+40°=100°.
∵DG平分∠ADC,
∴.
∵∠EBC=∠ABC﹣∠ABE=60°﹣10°=50°,
∴∠EBC=∠GDC.
∴DG∥BE.
23.解:(1)∠BDC=∠BAC+∠B+∠C.
连接AD并延长到点E,
∵∠BDE是△ABD的外角,
∴∠BDE=∠B+∠BAD.
同理,∠CDE=∠C+∠CAD,
则∠BDE+∠CDE=∠BAD+∠CAD+∠B+∠C.
又∠BDE+∠CDE=∠BDC,∠BAD+∠CAD=∠BAC,
∴∠BDC=∠BAC+∠B+∠C.
(2)①由(1)中的结论可知,
∠X=∠ABX+∠A+∠ACX.
又∠A=54°,∠X=90°,
∴∠ABX+∠ACX=36°.
②由(1)中的结论可知,
∠DBE=∠CDB+∠DCE+∠CEB,
则∠CDB+∠CEB=∠DBE﹣∠DCE.
又DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠CDB,∠AEC=∠CEB.
则∠ADC+∠AEC=∠CDB+∠CEB.
又∠DCE=∠ADC+∠DEA+∠AEC,
∴∠DCE=∠DBE﹣∠DCE+∠DAE.
即∠DCE=.
又∠DAE=α,∠DBE=β,
所以∠DCE=.
24.(1)解:∵BE、CE分别平分∠ABC和∠ACB,
∴,,
∵∠ECB+∠BEC+∠EBC=180°,
∴∠BEC=180°﹣(∠ECB+∠EBC)
=180°﹣(
=
=
=,
=105°,
(2)解:,理由如下:
∵BE平分∠ABC,CE平分∠ACD,BE和CE交于点E,
∴,.
∵∠ACD是△ABC的外角,∠ECD是△BCE的外角,
∴
(3)解:∵∠CBD与∠BCF是△ABC的外角,
∴∠CBD=∠ACB+∠A,∠BCF=∠ABC+∠A,
∵BE,CE分别是△ABC外角∠CBD和∠BCF的平分线,
∴,.
∵∠E+∠ECB+∠EBC=180°,
∴∠E=180°﹣∠ECB﹣∠EBC,
=,
=,
=.
25.解:(1)①∵△ABC是“友爱三角形”,且∠A与∠B互为“友爱角”(∠A>∠B),
∴∠A=2∠B,
∵∠ACB=90°,
∴∠A+∠B=180°﹣90°=90°,即2∠B+∠B=90°,解得∠B=30°,
∴∠A=60°;
②△ACD、△BCD都是“友爱三角形”,
理由:∵CD是△ABC中AB边上的高,
∴∠ADC=∠BDC=90°,
∵∠A=60°,∠B=30°,
∴∠ACD=30°,∠BCD=60°
在△ACD中,∠A=60°,∠ACD=30°,
∴,
∴△ACD为“友爱三角形”;
在△BCD中,∠BCD=60°,∠B=30°,
∴
∴△BCD为“友爱三角形”;
(2)∵△ACD是“友爱三角形”,D是边AB上一点(不与点A,B重合),
∴或,
当时,;
当时,
∴∠A+3∠ACD=180°,即3∠ACD=114°,
∴∠ACD=38°,
综上所述,∠ACD的度数为33°或38°.
26.解:(1)当B,D,C三点共线时,∠BDC=180°,
∵∠ABD=70°,∠ACD=40°,
∴∠BAC=180°﹣∠ABD﹣∠ACD=180°﹣70°﹣40°=70°,
∵AE平分∠BAC,DE平分∠BDC,
∴,,
∵∠BAE+∠ABD=∠AED+∠BDE,
∴35°+70°=∠AED+90°,
∴∠AED=15°,
(2)如图,连接BC,
∵AE平分∠BAC,DE平分∠BDC,
∴∠BAC=2∠BAE,∠BDC=2∠BDE,
∵2∠BAE+∠ABD+∠DBC+∠DCB+∠ACD=180°,∠B=50°,∠C=20°,
∴2∠BAE=180°﹣∠ABD﹣∠DBC﹣∠DCB﹣∠ACD
=180°﹣50°﹣∠DBC﹣∠DCB﹣20°
=110°﹣∠DBC﹣∠DCB,
∴,
∵2∠BDE+∠DBC+∠DCB=180°,
∴2∠BDE=180°﹣∠DBC﹣∠DCB,
∴,
∵∠BAE+∠ABD=∠AED+∠BDE,
∴,
∴∠AED=15°;
(3)如图,连接BC,
∵AE平分∠BAC,DE平分∠BDC,
∴∠BAC=2∠BAE,∠BDC=2∠BDE,
∵2∠BAE+∠ABD+∠DBC+∠DCB+∠ACD=180°,
∴2∠BAE=180°﹣∠ABD﹣∠DBC﹣∠DCB﹣∠ACD,
∴,
∵2∠BDE+∠DBC+∠DCB=180°,
∴2∠BDE=180°﹣∠DBC﹣∠DCB,
∴,
∵∠BAE+∠ABD=∠AED+∠BDE,
∴,
∴,即,
一.选择题(共10小题)
1.一个多边形的内角和是1260°,则这个多边形是( )
A.十边形 B.九边形 C.八边形 D.七边形
2.下列长度的各组线段中,能组成三角形的是( )
A.2,3,5 B.3,3,6 C.3,4,5 D.5,6,12
3.如图,在△ABC中,点E是BC的中点,AB=7,AC=10,△ACE的周长是25,则△ABE的周长是( )
A.18 B.22 C.28 D.32
4.画△ABC的边AC边的高,正确的是( )
A.B. C.D.
5.如图,△ABC中,AD为△ABC的角平分线,BE为△ABC的高,∠C=70°,∠ABC=48°,那么∠3是( )
A.59° B.60° C.56° D.22°
6.下列说法中,正确的是( )
A.三角形的三条高都在三角形内,且都相交于一点
B.三角形的一个外角大于任何一个内角
C.任意三角形的外角和都是360°
D.△ABC中,当,时,这个三角形是直角三角形
7.如图,直线a∥b,Rt△ABC的直角顶点A落在直线a上,点B落在直线b上,若∠1=15°,∠2=25°,则∠ABC的大小为( )
A.40° B.45° C.50° D.55°
8.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是( )
A.40° B.43° C.46° D.54°
9.如图,△ABC的两条内角平分线BO,CO相交于点O,两条外角平分线BP,CP相交于点P.已知∠BOC=120°,则∠P=( )
A.60° B.50° C.40° D.30°
10.如图,△ABC中,点O为三角形的重心,D为OC中点,若△ABC的面积为12,则△BOD的面积是( )
A.6 B.4 C.3 D.2
二.填空题(共8小题)
11.在日常生活中,大桥的钢架、索道的支架都采用了三角形结构,这里运用的三角形的性质是 .
12.如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是 .
13.在△ABC中,若∠A﹣∠B=50°,最小角为30°,则最大角为 .
14.如图,∠A+∠B+∠C+∠D+∠E+∠F= °.
15.已知a,b,c为三角形的三边长,化简:|a+b﹣c|﹣|c﹣a+b|+|a﹣b﹣c|= .
16.在△ABC中,若AB=5,AC=7,则中线AD的长的取值范围是 .
17.如图,∠1=∠2=25°,∠3=∠4,∠5=∠6,则∠7= .
18.如图,点D是△ABC的重心,连接AD并延长交BC于点E,AB=4,△ABE的周长比△ACE的周长大1.8,则AC= .
三.解答题(共8小题)
19.已知a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6.
(1)求c的取值范围;
(2)若△ABC的周长为14,求c的值.
20.如图,在△ABC中,AD为BC边上的高,CE平分∠ACD交AD于点E,若∠BAC:∠CAD=3:2,∠DCE=35°.
(1)求∠CAD的度数;
(2)求∠B的度数.
21.如图,AD、AE分别是△ABC的高和角平分线,∠B=40°,∠ACB=80°.点F在BC的延长线上,FG⊥AE,垂足为H,FG与AB相交于点G.
(1)求∠AGF的度数;
(2)求∠EAD的度数.
22.如图,在△ABC中,∠ABC=60°,∠ACB=40°,BE⊥AC于点E,AD与BE交于点F.
(1)求∠ABE的度数;
(2)若AD平分∠BAC,DG平分∠ADC,试说明DG∥BE.
23.如图1,像我们常见的学习用品——圆规,我们把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块直角三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=54°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=α,∠DBE=β,请用含α和β的式子表示∠DCE的度数.
24.下面是有关三角形内角、外角平分线的探究,阅读后请按要求作答:
(1)如图1,BE、CE分别是∠ABC和∠ACB的平分线且相交于点E,若∠A=30°,则∠E= ;
(2)如图2,BE平分∠ABC,CE平分∠ACD,BE和CE交于点E,猜想∠A与∠E之间的数量关系,并说明理由;
(3)如图3,BE,CE分别是△ABC外角∠CBD和∠BCF的平分线且相交于点E,直接写出∠A与∠E之间的数量关系.
25.定义:在一个三角形中,如果有一个角是另一个角的,我们称这两个角互为“友爱角”,这个三角形叫作“友爱三角形”.例如:在△ABC中,如果∠A=80°,∠B=40°,那么∠A与∠B互为“友爱角”,△ABC为“友爱三角形”.
(1)如图1,△ABC是“友爱三角形”,且∠A与∠B互为“友爱角”(∠A>∠B),∠ACB=90°.
①求∠A、∠B的度数.
②若CD是△ABC中AB边上的高,则△ACD、△BCD都是“友爱三角形”吗?为什么?
(2)如图2,在△ABC中,∠ACB=70°,∠A=66°,D是边AB上一点(不与点A,B重合),连接CD,若△ACD是“友爱三角形”,直接写出∠ACD的度数.
26.点D为∠BAC内一点,连接BD,CD,∠B>∠C,0°<∠BDC≤180°,∠BAC,∠BDC的平分线交于点E.
(1)如图1,当B,D,C三点共线时,若∠ABD=70°,∠ACD=40°,直接写出∠AED的度数是 ;
(2)如图2,若∠B=50°,∠C=20°,求∠AED;
(3)直接写出∠B,∠C,∠AED之间的数量关系是 .
参考答案
一.选择题(共10小题)
1.B.
2.C.
3.B.
4.D.
5.A.
6.C.
7.C.
8.A.
9.A.
10.D.
二.填空题(共8小题)
11.三角形的稳定性.
12.80°.
13.100°或80°.
14.360.
15.a+b﹣c.
16.1<AD<6.
17.100°.
18.2.2.
三.解答题(共8小题)
19.解:(1)∵a,b,c分别为△ABC的三边,且满足a+b=3c﹣2,a﹣b=2c﹣6,
∴a+b=3c﹣2>c,a﹣b=2c﹣6<c,
∴,
解得,1<c<6,
∴c的取值范围为1<c<6;
(2)由题意知,a+b+c=3c﹣2+c=14,
解得,c=4,
∴c的值为4.
20.解:(1)∵CE平分∠ACD,
∴∠DCA=2∠DCE,
∵∠DCE=35°,
∴∠DCA=2∠DCE=2×35°=70°,
∵AD为BC边上的高,
∴∠ADB=90°,
∴∠CAD=90°﹣∠DCA=20°;
(2)∵∠BAC:∠CAD=3:2,∠CAD=20°,
∴∠BAC=30°,
∴∠BAD=∠BAC+∠CAD=20°+30°=50°,
∴∠B=90°﹣∠BAD=90°﹣50°=40°.
21.解:(1)∵∠B=40°,∠ACB=80°,
∴∠BAC=180°﹣40°﹣80°=60°,
∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=30°,
∵FG⊥AE,
∴∠AHG=90°,
∴∠AGF=180°﹣90°﹣30°=60°;
(2)∵AD是△ABC的高,
∴∠ADC=90°,
∵∠ACB=80°,
∴∠CAD=180°﹣90°﹣80°=10°,
∵∠BAC=60°,AE是△ABC的角平分线,
∴∠CAE=∠BAC=30°,
∴∠EAD=∠CAE﹣∠CAD=30°﹣10°=20°.
22.解:(1)∵∠ABC+∠BAC+∠ACB=180°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣60°﹣40°=80°.
∵AC⊥BE,
∴∠AEB=90°,
∴∠ABE=90°﹣∠BAC=90°﹣80°=10°.
(2)∵AD平分∠BAC,
∴,
∴∠ADC=∠ABC+∠BAD=60°+40°=100°.
∵DG平分∠ADC,
∴.
∵∠EBC=∠ABC﹣∠ABE=60°﹣10°=50°,
∴∠EBC=∠GDC.
∴DG∥BE.
23.解:(1)∠BDC=∠BAC+∠B+∠C.
连接AD并延长到点E,
∵∠BDE是△ABD的外角,
∴∠BDE=∠B+∠BAD.
同理,∠CDE=∠C+∠CAD,
则∠BDE+∠CDE=∠BAD+∠CAD+∠B+∠C.
又∠BDE+∠CDE=∠BDC,∠BAD+∠CAD=∠BAC,
∴∠BDC=∠BAC+∠B+∠C.
(2)①由(1)中的结论可知,
∠X=∠ABX+∠A+∠ACX.
又∠A=54°,∠X=90°,
∴∠ABX+∠ACX=36°.
②由(1)中的结论可知,
∠DBE=∠CDB+∠DCE+∠CEB,
则∠CDB+∠CEB=∠DBE﹣∠DCE.
又DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠CDB,∠AEC=∠CEB.
则∠ADC+∠AEC=∠CDB+∠CEB.
又∠DCE=∠ADC+∠DEA+∠AEC,
∴∠DCE=∠DBE﹣∠DCE+∠DAE.
即∠DCE=.
又∠DAE=α,∠DBE=β,
所以∠DCE=.
24.(1)解:∵BE、CE分别平分∠ABC和∠ACB,
∴,,
∵∠ECB+∠BEC+∠EBC=180°,
∴∠BEC=180°﹣(∠ECB+∠EBC)
=180°﹣(
=
=
=,
=105°,
(2)解:,理由如下:
∵BE平分∠ABC,CE平分∠ACD,BE和CE交于点E,
∴,.
∵∠ACD是△ABC的外角,∠ECD是△BCE的外角,
∴
(3)解:∵∠CBD与∠BCF是△ABC的外角,
∴∠CBD=∠ACB+∠A,∠BCF=∠ABC+∠A,
∵BE,CE分别是△ABC外角∠CBD和∠BCF的平分线,
∴,.
∵∠E+∠ECB+∠EBC=180°,
∴∠E=180°﹣∠ECB﹣∠EBC,
=,
=,
=.
25.解:(1)①∵△ABC是“友爱三角形”,且∠A与∠B互为“友爱角”(∠A>∠B),
∴∠A=2∠B,
∵∠ACB=90°,
∴∠A+∠B=180°﹣90°=90°,即2∠B+∠B=90°,解得∠B=30°,
∴∠A=60°;
②△ACD、△BCD都是“友爱三角形”,
理由:∵CD是△ABC中AB边上的高,
∴∠ADC=∠BDC=90°,
∵∠A=60°,∠B=30°,
∴∠ACD=30°,∠BCD=60°
在△ACD中,∠A=60°,∠ACD=30°,
∴,
∴△ACD为“友爱三角形”;
在△BCD中,∠BCD=60°,∠B=30°,
∴
∴△BCD为“友爱三角形”;
(2)∵△ACD是“友爱三角形”,D是边AB上一点(不与点A,B重合),
∴或,
当时,;
当时,
∴∠A+3∠ACD=180°,即3∠ACD=114°,
∴∠ACD=38°,
综上所述,∠ACD的度数为33°或38°.
26.解:(1)当B,D,C三点共线时,∠BDC=180°,
∵∠ABD=70°,∠ACD=40°,
∴∠BAC=180°﹣∠ABD﹣∠ACD=180°﹣70°﹣40°=70°,
∵AE平分∠BAC,DE平分∠BDC,
∴,,
∵∠BAE+∠ABD=∠AED+∠BDE,
∴35°+70°=∠AED+90°,
∴∠AED=15°,
(2)如图,连接BC,
∵AE平分∠BAC,DE平分∠BDC,
∴∠BAC=2∠BAE,∠BDC=2∠BDE,
∵2∠BAE+∠ABD+∠DBC+∠DCB+∠ACD=180°,∠B=50°,∠C=20°,
∴2∠BAE=180°﹣∠ABD﹣∠DBC﹣∠DCB﹣∠ACD
=180°﹣50°﹣∠DBC﹣∠DCB﹣20°
=110°﹣∠DBC﹣∠DCB,
∴,
∵2∠BDE+∠DBC+∠DCB=180°,
∴2∠BDE=180°﹣∠DBC﹣∠DCB,
∴,
∵∠BAE+∠ABD=∠AED+∠BDE,
∴,
∴∠AED=15°;
(3)如图,连接BC,
∵AE平分∠BAC,DE平分∠BDC,
∴∠BAC=2∠BAE,∠BDC=2∠BDE,
∵2∠BAE+∠ABD+∠DBC+∠DCB+∠ACD=180°,
∴2∠BAE=180°﹣∠ABD﹣∠DBC﹣∠DCB﹣∠ACD,
∴,
∵2∠BDE+∠DBC+∠DCB=180°,
∴2∠BDE=180°﹣∠DBC﹣∠DCB,
∴,
∵∠BAE+∠ABD=∠AED+∠BDE,
∴,
∴,即,
