第十一章 三角形 复习试题(含答案) 2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 复习试题(含答案) 2024—2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 319.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-29 00:00:00 | ||
图片预览



文档简介
人教版数学八年级上第十一章《三角形》复习试题
一.选择题(共10小题)
1.多边形的内角和不可能为( )
A.180° B.540° C.1200° D.1800°
2.以下各组长度的线段为边,能构成三角形的是( )
A.8cm、5cm、3cm B.6cm、8cm、15cm C.8cm、4cm、3cm D.4cm、6cm、5cm
3.如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
4.下列各图形中,BD是△ABC的高的图形是( )
A.B. C.D.
5.如果三角形的三个内角度数比为1:1:2,则这个三角形为( )
A.锐角三角形 B.钝角三角形
C.非等腰直角三角形 D.等腰直角三角形
6.如图:在△ABC中,AD平分∠BAC交BC于D,AE⊥BC于E,∠B=40°,∠BAC=80°,则∠DAE=( )
A.7° B.8° C.9° D.10°
7.如图,△ABC中∠ACB=90°,且CD∥AB.∠B=60°,则∠1等于( )
A.30° B.40° C.50° D.60°
8.如图,在△ABC中,∠A=60°,∠C=70°,BD平分∠ABC,DE∥BC,则∠BDE的度数是( )
A.50° B.35° C.30° D.25°
9.有一道题目“在△ABC中,AD是边BC上的高,∠ABC的平分线与边AC交于点F.若∠ABC=50°,∠CAD=20°,求∠BFA的度数.”对于其答案,甲答:∠BFA=110°,乙答:∠BFA=95°,丙答:∠BFA=135°.则正确的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有乙
10.如图,△ABC的两条中线CD、BE交于点F,若四边形ADFE的面积为18,则△ABC的面积是( )
A.55 B.54 C.42 D.41
二.填空题(共8小题)
11.如图所示的自行车架设计成三角形,这样做的依据是三角形具有 .
12.如图,已知∠O=30°,点P是射线OB上一个动点,设∠APO=x°,要使△APO是钝角三角形,则x的取值范围为 .
13.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠ACB=78°,点F为边AB上一点,当△BDF为直角三角形时,则∠ADF的度数为 .
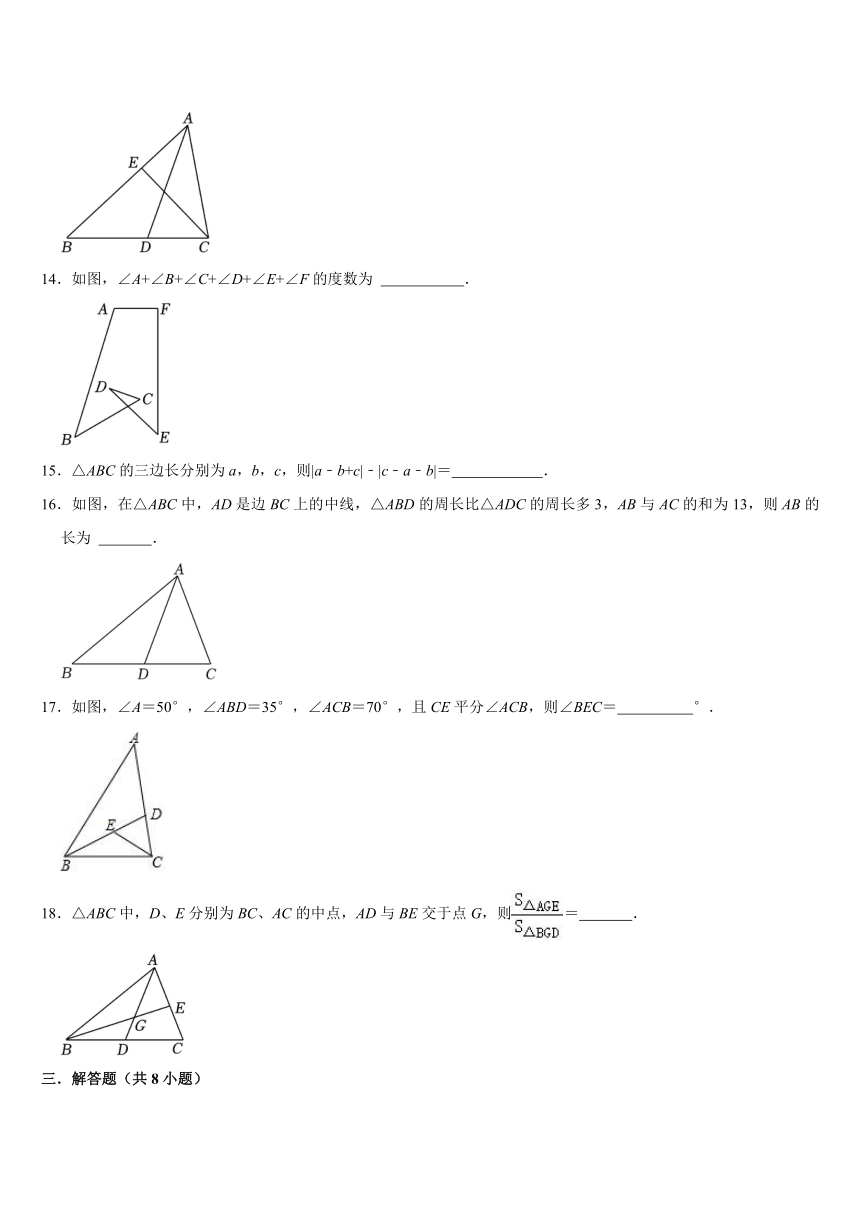
14.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为 .
15.△ABC的三边长分别为a,b,c,则|a﹣b+c|﹣|c﹣a﹣b|= .
16.如图,在△ABC中,AD是边BC上的中线,△ABD的周长比△ADC的周长多3,AB与AC的和为13,则AB的长为 .
17.如图,∠A=50°,∠ABD=35°,∠ACB=70°,且CE平分∠ACB,则∠BEC= °.
18.△ABC中,D、E分别为BC、AC的中点,AD与BE交于点G,则= .
三.解答题(共8小题)
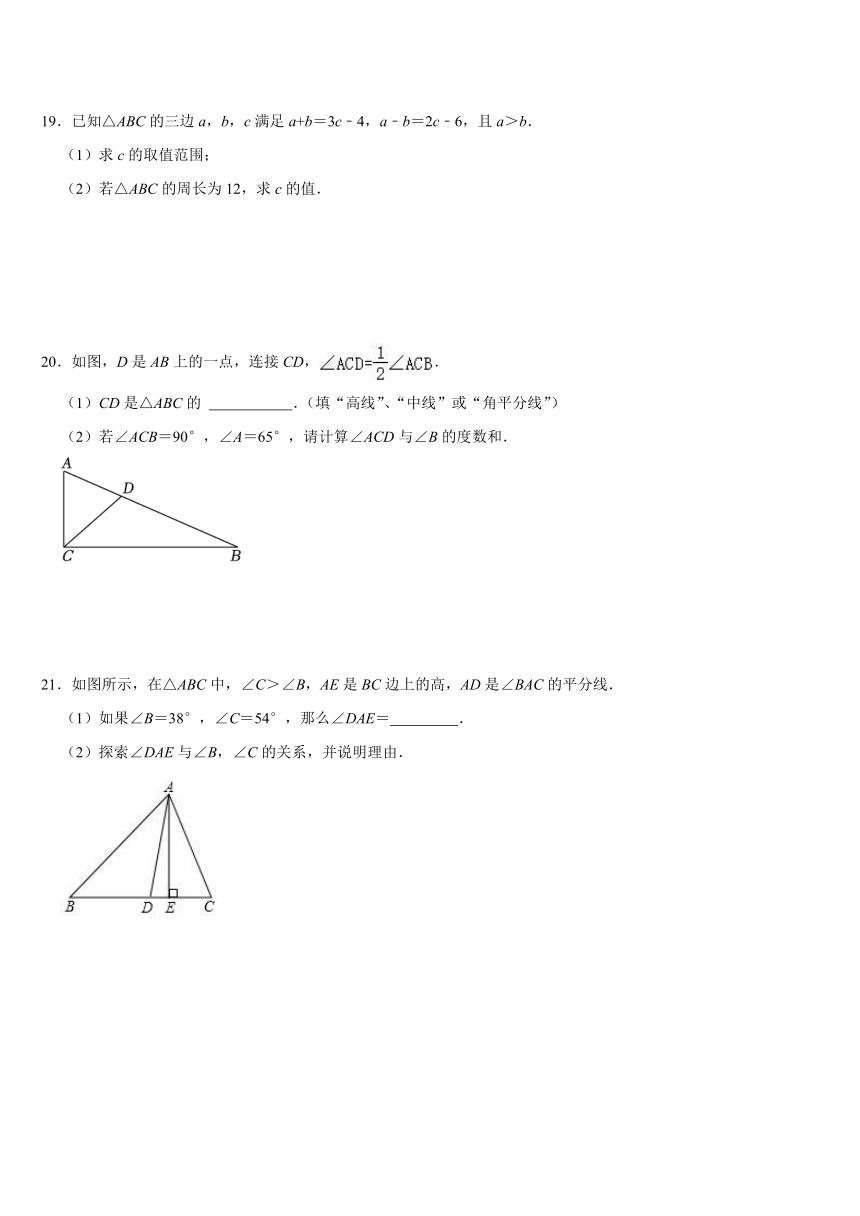
19.已知△ABC的三边a,b,c满足a+b=3c﹣4,a﹣b=2c﹣6,且a>b.
(1)求c的取值范围;
(2)若△ABC的周长为12,求c的值.
20.如图,D是AB上的一点,连接CD,.
(1)CD是△ABC的 .(填“高线”、“中线”或“角平分线”)
(2)若∠ACB=90°,∠A=65°,请计算∠ACD与∠B的度数和.
21.如图所示,在△ABC中,∠C>∠B,AE是BC边上的高,AD是∠BAC的平分线.
(1)如果∠B=38°,∠C=54°,那么∠DAE= .
(2)探索∠DAE与∠B,∠C的关系,并说明理由.
22.如图,△ABC的三个内角的角平分线交于点O,过点O作∠ODB=∠AOB,交BC于点D,△ABC的外角∠ACE的角平分线交BO的延长线于点F.
(1)试判断OC与OD的位置关系,并说明理由.
(2)求证:CF∥OD.
23.如图,△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠BAD;∠DAE的度数.
24.(1)如图1,在△ABC中,∠ABC和∠ACB的平分线交于点O,则有∠BOC=90°+∠A,请说明理由;
(2)如图2,在△ABC中,内角∠ABC的平分线和外角∠ACD的平分线交于点O,请直接写出∠BOC与∠BAC的关系,不必说明理由;
(3)如图3,AP,BP分别平分∠CAD,∠CBD,则有∠P=(∠C+∠D),请说明理由;
(4)如图4,AP,BP分别平分∠CAM,∠CBD,请直接写出∠P与∠C,∠D的关系,不必说明理由.
25.在△ABC中,点E是CA延长线上一点.
(1)如图1,过点B作BD⊥BC,交CE于点F,∠D=∠C.
①若∠C=36°,则∠DAF= °;
②试写出∠DAF与∠C的数量关系,并说明理由;
③当∠DAF=∠D时,求∠C的度数;
④若∠D=∠ABD,请说明BA⊥CF.
(2)如图2,BD交CE于点F,∠D=∠C,直接写出∠DAC、∠C与∠DBC之间的数量关系.
26.【教材呈现]如图是华师版七年级下册数学教材第76页的部分内容.
(1)请根据教材提示,结合图①,将证明过程补充完整;
【结论应用】
(2)如图②,在△ABC中,∠A=60°,BP平分∠ABC,CP平分∠ACB,求∠P的度数.
参考答案
一.选择题(共10小题)
1.C.
2.D.
3.A.
4.C.
5.D.
6.D.
7.A.
8.D.
9.B.
10.B.
二.填空题(共8小题)
11.稳定性.
12.0°<x<60°或90°<x<150°.
13.60°或18°.
14.360°.
15.2c﹣2b.
16.8.
17.120.
18.1.
三.解答题(共8小题)
19.解:(1)由题意有,a﹣b<c<a+b,
∴2c﹣6<c<3c﹣4,
∴2<c<6,
又∵a>b,
∴a﹣b=2c﹣6>0,
∴c>3,而2<c<6,
∴c的取值范围为:3<c<6;
(2)∵△ABC周长为12,
∴,
∴a=5,b=3,c=4.
20.解:(1)∵∠ACD=∠ACB,
∴∠ACD=∠DCB,
∴CD是△ABC的角平分线,
(2)∵∠ACD=∠ACB,∠ACB=90°,
∴∠ACD=×90°=45°,
∵∠ACB=90°,∠A=65°,
∴∠B=90°﹣65°=25°,
∴∠ACD+∠B=45°+25°=70°.
21.解:在△ABC中,∵∠B=38°,∠C=54°,
∴∠BAC=180°﹣∠B﹣∠C=88°,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAC=44°,
∵AE是BC边上的高,
∴∠AEC=90°,
在△AEC中,∠AEC=90°,∠C=54°,
∴∠EAC=180°﹣∠AEC﹣∠C=36°,
∴∠DAE=∠DAC﹣∠EAC=8°.
(2)∠DAE=.
理由:设∠B=α,∠C=β,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣α﹣β,
∵D是∠BAC的平分线,
∴∠DAC=∠BAC=90°﹣α﹣β,
∵AE是BC边上的高,
∴∠AEC=90°,
∴∠EAC=180°﹣∠AEC﹣∠C=90°﹣β,
∴∠DAE=∠DAC﹣∠EAC=(90°﹣α﹣β)﹣(90°﹣β)=.
即∠DAE=.
22.(1)解:OC⊥OD.
∵三角形的三条角平分线交于点O,
∴,
∵∠AOB=∠ODB=∠COD+∠OCD,
∴,
又∵,
∴∠COD=90°,
∴OC⊥OD;
(2)证明:∵CF平分∠ACE,CO平分∠ACB,
∴,
∴.
即∠FCO=90°.
∵∠COD=90°,
∴∠FCO=∠COD.
∴CF∥OD.
23.解:∵AD⊥BC,
∴∠BDA=∠CDA=90°,
∵∠B=70°,
∴∠BAD=90°﹣∠B=90°﹣70°=20°,
∵∠B=70°,∠C=34°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣34°=76°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=BAC=76°=38°,
∴∠DAE=∠BAE﹣∠BAD=38°﹣20°=18°.
24.解:(1)在△ABC,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∵BO是∠ABC的平分线,
∴∠1=∠ABC,
∵CO是∠ACB的平分线,
∴∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB)=90°﹣∠A,
在△BOC,∠BOC+∠1+∠2=180°,
∴∠BOC=180°﹣(∠1+∠2)=90°+∠A;
(2)∠BOC=∠BAC.
∵CO是∠ACD的角平分线,
∴∠OCD=∠ACD.
又∵∠ACD=∠BAC+∠ABC,
∴∠OCD=∠BAC+∠ABC,
又∵∠OCD=∠BOC+∠ABC,
∴∠BAC+∠ABC=∠BOC+∠ABC,
∴∠BOC=∠BAC.
(3)∵AP、BP分别平分∠CAD、∠CBD,
∴∠DAP=∠CAP=∠CAD,∠CBP=∠DBP=∠CBD,
∵∠AEB是△ADE和△BEP的外角,
∴∠AEB=∠D+∠DAP=∠DBP+∠P,
∴∠D+∠CAD=∠CBD+∠P,
∴∠CAD﹣∠CBD=∠P﹣∠D,
∵∠AFB是△BCF和△AFP的外角,
∴∠AFB=∠CAP+∠P=∠CBP+∠C,
∴∠CAD+∠P=∠CBD+∠C,
∴∠CAD﹣∠CBD=∠C﹣∠P,
∵∠CAD﹣∠CBD=∠P﹣∠D,
∴∠C﹣∠P=∠P﹣∠D,
∴∠P=.
(4)∠P=90°+(∠C+∠D).
理由如下:
∵AP,BP分别平分∠CAM,∠CBD,
∴∠MAP=∠CAP,∠EBP=∠PBC,
∵∠AGD=BGC,
∴∠D+∠DAC=∠C+∠CBE,
∴∠D+180°﹣2∠CAE=∠C+2∠PBE,
∴∠PBE+∠CAE=,
∵∠AED=∠BEP,
∴∠P+∠PBE=∠D+∠DAE,
∴∠P+∠PBE=∠D+180°﹣∠EAM=∠D+180°﹣∠CAE,
∴∠P=∠D+180°﹣
=90°+D+C=90°+(∠C+∠D).
25.解:(1)①∵BD⊥BC,
∴∠CBF=90°,
∵∠C=36°,∠D=∠C,
∴∠D=∠C=36°,
∴∠BFC=90°﹣∠C=90°﹣36°=54°,
∵∠BFC=∠D+∠DAF,
∴∠DAF=∠BFC﹣∠D=54°﹣36°=18°;
②∵BD⊥BC,
∴∠CBF=90°,
∴∠BFC=90°﹣∠C,
∵∠BFC=∠D+∠DAF,
∴∠DAF=∠BFC﹣∠D=90°﹣∠C﹣∠D,
∵∠D=∠C,
∴∠DAF=90°﹣∠C﹣∠D=90°﹣2∠C;
③当∠DAF=∠D时,
∵∠D=∠C,
∴∠DAF=∠C=∠D,
由②知,∠DAF=90°﹣2∠C,
∴∠C=90°﹣2∠C,
∴∠C=30°;
④当∠D=∠ABD时,
∵∠D=∠C,
∴∠ABD=∠C=∠D,
由②知,∠DAF=90°﹣2∠C,
∴∠BAF=180°﹣∠ABD﹣∠D﹣∠DAF=180°﹣2∠C﹣(90°﹣2∠C)=90°,
∴BA⊥CF;
(2)∵∠DAC=∠D+∠AFD,
又∵∠AFD=∠C+∠DBC,
∴∠DAC=∠D+∠C+∠DBC,
∵∠D=∠C,
∴∠DAC=2∠C+∠DBC.
26.解:(1)延长BC至点E,以点C为顶点,在BE的上侧作∠DCE=∠2,则CD∥BA,
∴∠ACD=∠1(两直线平行,内错角相等),
∵∠3+∠ACD+∠DCE=180°(平角的定义),
∴∠1+∠2+∠3=180°(等量代换);
(2)∵BP平分∠ABC,CP平分∠ACB,
∴∠ABP=∠PBC=∠ABC,∠ACP=∠PCB=∠ACB,
∵∠P+∠PBC+∠PCB=180°,∠A+∠ABC+∠ACB=180°,
∴∠P=180°﹣∠PBC﹣∠PCB
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=90°+∠A,
∵∠A=60°,
∴∠P=90°+×60°=120°.
一.选择题(共10小题)
1.多边形的内角和不可能为( )
A.180° B.540° C.1200° D.1800°
2.以下各组长度的线段为边,能构成三角形的是( )
A.8cm、5cm、3cm B.6cm、8cm、15cm C.8cm、4cm、3cm D.4cm、6cm、5cm
3.如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
4.下列各图形中,BD是△ABC的高的图形是( )
A.B. C.D.
5.如果三角形的三个内角度数比为1:1:2,则这个三角形为( )
A.锐角三角形 B.钝角三角形
C.非等腰直角三角形 D.等腰直角三角形
6.如图:在△ABC中,AD平分∠BAC交BC于D,AE⊥BC于E,∠B=40°,∠BAC=80°,则∠DAE=( )
A.7° B.8° C.9° D.10°
7.如图,△ABC中∠ACB=90°,且CD∥AB.∠B=60°,则∠1等于( )
A.30° B.40° C.50° D.60°
8.如图,在△ABC中,∠A=60°,∠C=70°,BD平分∠ABC,DE∥BC,则∠BDE的度数是( )
A.50° B.35° C.30° D.25°
9.有一道题目“在△ABC中,AD是边BC上的高,∠ABC的平分线与边AC交于点F.若∠ABC=50°,∠CAD=20°,求∠BFA的度数.”对于其答案,甲答:∠BFA=110°,乙答:∠BFA=95°,丙答:∠BFA=135°.则正确的是( )
A.甲和乙 B.乙和丙 C.甲和丙 D.只有乙
10.如图,△ABC的两条中线CD、BE交于点F,若四边形ADFE的面积为18,则△ABC的面积是( )
A.55 B.54 C.42 D.41
二.填空题(共8小题)
11.如图所示的自行车架设计成三角形,这样做的依据是三角形具有 .
12.如图,已知∠O=30°,点P是射线OB上一个动点,设∠APO=x°,要使△APO是钝角三角形,则x的取值范围为 .
13.如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠ACB=78°,点F为边AB上一点,当△BDF为直角三角形时,则∠ADF的度数为 .
14.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为 .
15.△ABC的三边长分别为a,b,c,则|a﹣b+c|﹣|c﹣a﹣b|= .
16.如图,在△ABC中,AD是边BC上的中线,△ABD的周长比△ADC的周长多3,AB与AC的和为13,则AB的长为 .
17.如图,∠A=50°,∠ABD=35°,∠ACB=70°,且CE平分∠ACB,则∠BEC= °.
18.△ABC中,D、E分别为BC、AC的中点,AD与BE交于点G,则= .
三.解答题(共8小题)
19.已知△ABC的三边a,b,c满足a+b=3c﹣4,a﹣b=2c﹣6,且a>b.
(1)求c的取值范围;
(2)若△ABC的周长为12,求c的值.
20.如图,D是AB上的一点,连接CD,.
(1)CD是△ABC的 .(填“高线”、“中线”或“角平分线”)
(2)若∠ACB=90°,∠A=65°,请计算∠ACD与∠B的度数和.
21.如图所示,在△ABC中,∠C>∠B,AE是BC边上的高,AD是∠BAC的平分线.
(1)如果∠B=38°,∠C=54°,那么∠DAE= .
(2)探索∠DAE与∠B,∠C的关系,并说明理由.
22.如图,△ABC的三个内角的角平分线交于点O,过点O作∠ODB=∠AOB,交BC于点D,△ABC的外角∠ACE的角平分线交BO的延长线于点F.
(1)试判断OC与OD的位置关系,并说明理由.
(2)求证:CF∥OD.
23.如图,△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34°,求∠BAD;∠DAE的度数.
24.(1)如图1,在△ABC中,∠ABC和∠ACB的平分线交于点O,则有∠BOC=90°+∠A,请说明理由;
(2)如图2,在△ABC中,内角∠ABC的平分线和外角∠ACD的平分线交于点O,请直接写出∠BOC与∠BAC的关系,不必说明理由;
(3)如图3,AP,BP分别平分∠CAD,∠CBD,则有∠P=(∠C+∠D),请说明理由;
(4)如图4,AP,BP分别平分∠CAM,∠CBD,请直接写出∠P与∠C,∠D的关系,不必说明理由.
25.在△ABC中,点E是CA延长线上一点.
(1)如图1,过点B作BD⊥BC,交CE于点F,∠D=∠C.
①若∠C=36°,则∠DAF= °;
②试写出∠DAF与∠C的数量关系,并说明理由;
③当∠DAF=∠D时,求∠C的度数;
④若∠D=∠ABD,请说明BA⊥CF.
(2)如图2,BD交CE于点F,∠D=∠C,直接写出∠DAC、∠C与∠DBC之间的数量关系.
26.【教材呈现]如图是华师版七年级下册数学教材第76页的部分内容.
(1)请根据教材提示,结合图①,将证明过程补充完整;
【结论应用】
(2)如图②,在△ABC中,∠A=60°,BP平分∠ABC,CP平分∠ACB,求∠P的度数.
参考答案
一.选择题(共10小题)
1.C.
2.D.
3.A.
4.C.
5.D.
6.D.
7.A.
8.D.
9.B.
10.B.
二.填空题(共8小题)
11.稳定性.
12.0°<x<60°或90°<x<150°.
13.60°或18°.
14.360°.
15.2c﹣2b.
16.8.
17.120.
18.1.
三.解答题(共8小题)
19.解:(1)由题意有,a﹣b<c<a+b,
∴2c﹣6<c<3c﹣4,
∴2<c<6,
又∵a>b,
∴a﹣b=2c﹣6>0,
∴c>3,而2<c<6,
∴c的取值范围为:3<c<6;
(2)∵△ABC周长为12,
∴,
∴a=5,b=3,c=4.
20.解:(1)∵∠ACD=∠ACB,
∴∠ACD=∠DCB,
∴CD是△ABC的角平分线,
(2)∵∠ACD=∠ACB,∠ACB=90°,
∴∠ACD=×90°=45°,
∵∠ACB=90°,∠A=65°,
∴∠B=90°﹣65°=25°,
∴∠ACD+∠B=45°+25°=70°.
21.解:在△ABC中,∵∠B=38°,∠C=54°,
∴∠BAC=180°﹣∠B﹣∠C=88°,
∵AD是∠BAC的平分线,
∴∠DAC=∠BAC=44°,
∵AE是BC边上的高,
∴∠AEC=90°,
在△AEC中,∠AEC=90°,∠C=54°,
∴∠EAC=180°﹣∠AEC﹣∠C=36°,
∴∠DAE=∠DAC﹣∠EAC=8°.
(2)∠DAE=.
理由:设∠B=α,∠C=β,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣α﹣β,
∵D是∠BAC的平分线,
∴∠DAC=∠BAC=90°﹣α﹣β,
∵AE是BC边上的高,
∴∠AEC=90°,
∴∠EAC=180°﹣∠AEC﹣∠C=90°﹣β,
∴∠DAE=∠DAC﹣∠EAC=(90°﹣α﹣β)﹣(90°﹣β)=.
即∠DAE=.
22.(1)解:OC⊥OD.
∵三角形的三条角平分线交于点O,
∴,
∵∠AOB=∠ODB=∠COD+∠OCD,
∴,
又∵,
∴∠COD=90°,
∴OC⊥OD;
(2)证明:∵CF平分∠ACE,CO平分∠ACB,
∴,
∴.
即∠FCO=90°.
∵∠COD=90°,
∴∠FCO=∠COD.
∴CF∥OD.
23.解:∵AD⊥BC,
∴∠BDA=∠CDA=90°,
∵∠B=70°,
∴∠BAD=90°﹣∠B=90°﹣70°=20°,
∵∠B=70°,∠C=34°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣34°=76°,
∵AE平分∠BAC,
∴∠BAE=∠CAE=BAC=76°=38°,
∴∠DAE=∠BAE﹣∠BAD=38°﹣20°=18°.
24.解:(1)在△ABC,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∵BO是∠ABC的平分线,
∴∠1=∠ABC,
∵CO是∠ACB的平分线,
∴∠2=∠ACB,
∴∠1+∠2=(∠ABC+∠ACB)=90°﹣∠A,
在△BOC,∠BOC+∠1+∠2=180°,
∴∠BOC=180°﹣(∠1+∠2)=90°+∠A;
(2)∠BOC=∠BAC.
∵CO是∠ACD的角平分线,
∴∠OCD=∠ACD.
又∵∠ACD=∠BAC+∠ABC,
∴∠OCD=∠BAC+∠ABC,
又∵∠OCD=∠BOC+∠ABC,
∴∠BAC+∠ABC=∠BOC+∠ABC,
∴∠BOC=∠BAC.
(3)∵AP、BP分别平分∠CAD、∠CBD,
∴∠DAP=∠CAP=∠CAD,∠CBP=∠DBP=∠CBD,
∵∠AEB是△ADE和△BEP的外角,
∴∠AEB=∠D+∠DAP=∠DBP+∠P,
∴∠D+∠CAD=∠CBD+∠P,
∴∠CAD﹣∠CBD=∠P﹣∠D,
∵∠AFB是△BCF和△AFP的外角,
∴∠AFB=∠CAP+∠P=∠CBP+∠C,
∴∠CAD+∠P=∠CBD+∠C,
∴∠CAD﹣∠CBD=∠C﹣∠P,
∵∠CAD﹣∠CBD=∠P﹣∠D,
∴∠C﹣∠P=∠P﹣∠D,
∴∠P=.
(4)∠P=90°+(∠C+∠D).
理由如下:
∵AP,BP分别平分∠CAM,∠CBD,
∴∠MAP=∠CAP,∠EBP=∠PBC,
∵∠AGD=BGC,
∴∠D+∠DAC=∠C+∠CBE,
∴∠D+180°﹣2∠CAE=∠C+2∠PBE,
∴∠PBE+∠CAE=,
∵∠AED=∠BEP,
∴∠P+∠PBE=∠D+∠DAE,
∴∠P+∠PBE=∠D+180°﹣∠EAM=∠D+180°﹣∠CAE,
∴∠P=∠D+180°﹣
=90°+D+C=90°+(∠C+∠D).
25.解:(1)①∵BD⊥BC,
∴∠CBF=90°,
∵∠C=36°,∠D=∠C,
∴∠D=∠C=36°,
∴∠BFC=90°﹣∠C=90°﹣36°=54°,
∵∠BFC=∠D+∠DAF,
∴∠DAF=∠BFC﹣∠D=54°﹣36°=18°;
②∵BD⊥BC,
∴∠CBF=90°,
∴∠BFC=90°﹣∠C,
∵∠BFC=∠D+∠DAF,
∴∠DAF=∠BFC﹣∠D=90°﹣∠C﹣∠D,
∵∠D=∠C,
∴∠DAF=90°﹣∠C﹣∠D=90°﹣2∠C;
③当∠DAF=∠D时,
∵∠D=∠C,
∴∠DAF=∠C=∠D,
由②知,∠DAF=90°﹣2∠C,
∴∠C=90°﹣2∠C,
∴∠C=30°;
④当∠D=∠ABD时,
∵∠D=∠C,
∴∠ABD=∠C=∠D,
由②知,∠DAF=90°﹣2∠C,
∴∠BAF=180°﹣∠ABD﹣∠D﹣∠DAF=180°﹣2∠C﹣(90°﹣2∠C)=90°,
∴BA⊥CF;
(2)∵∠DAC=∠D+∠AFD,
又∵∠AFD=∠C+∠DBC,
∴∠DAC=∠D+∠C+∠DBC,
∵∠D=∠C,
∴∠DAC=2∠C+∠DBC.
26.解:(1)延长BC至点E,以点C为顶点,在BE的上侧作∠DCE=∠2,则CD∥BA,
∴∠ACD=∠1(两直线平行,内错角相等),
∵∠3+∠ACD+∠DCE=180°(平角的定义),
∴∠1+∠2+∠3=180°(等量代换);
(2)∵BP平分∠ABC,CP平分∠ACB,
∴∠ABP=∠PBC=∠ABC,∠ACP=∠PCB=∠ACB,
∵∠P+∠PBC+∠PCB=180°,∠A+∠ABC+∠ACB=180°,
∴∠P=180°﹣∠PBC﹣∠PCB
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=90°+∠A,
∵∠A=60°,
∴∠P=90°+×60°=120°.
