方程的根与函数的零点
图片预览




文档简介
课件13张PPT。3.1.1方程的根与函数的零点一元二次方程 ( )的
根与二次函数 的图象有
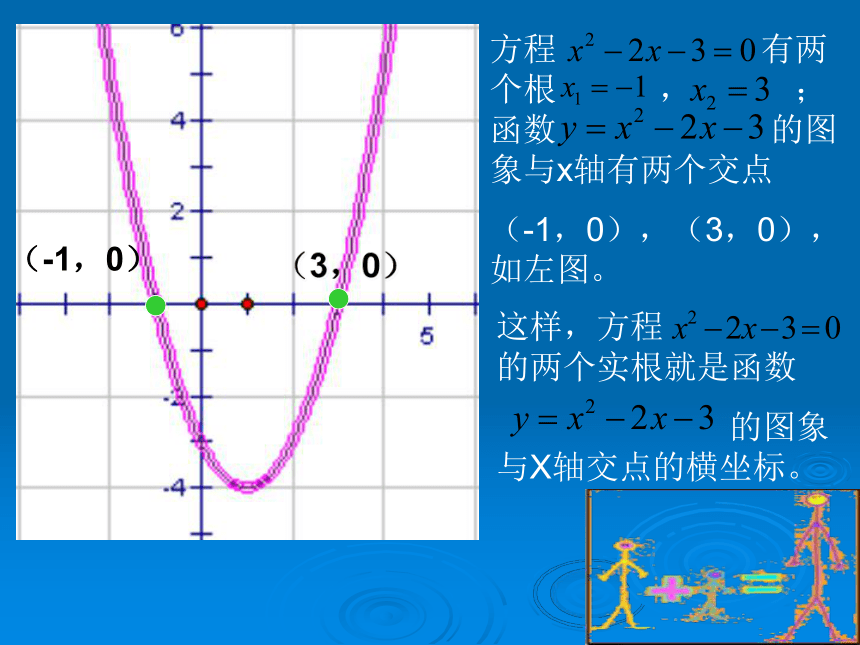
什么关系?思考?先观察几个具体的一元二次方程及其相应的二次函数,如:方程 与函数 方程 与函数方程 与函数(3,0)(-1,0)这样,方程 的两个实根就是函数
的图象与X轴交点的横坐标。方程 有两个根 , ;函数 的图象与x轴有两个交点
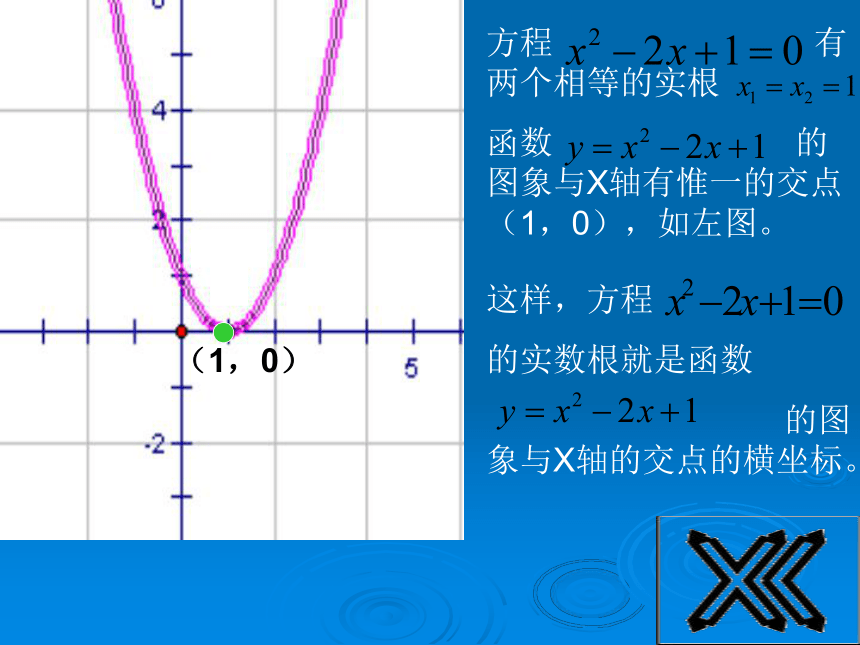
(-1,0),(3,0),如左图。方程 有两个相等的实根
函数 的图象与X轴有惟一的交点(1,0),如左图。 这样,方程
的实数根就是函数
的图象与X轴的交点的横坐标。(1,0)方程 无实数根,函数
的图象与X轴没有交点,如左图。上述关系对一般的一元二次方程
及其相应的二次函数 也成立。零点的概念对于函数 ,我们把使 的实数X叫做函数 的零点。这样,函数 的零点就是方程 的实数根,也就是函数 的图象与X轴的交点的横坐标,所以方程 有实数根 函数 有零点
函数 的图象与X轴有交点由些可知,求方程 的实数根,就是确定函数
的零点。函数零点的求法:
①(代数法)求方程 的根。②(几何法)
对于不能用求根公式的方程,可以将它与函数
的图象联系起来,并利用函数的性质找出零点. 二次函数设判别式 ,我们有:
(1)当 时,一元二次方程有两个不等的实数
根 ,相应的二次函数的图象与X轴有两个交点
( ,0),( ,0)为二次函数的两个零点。
(2)当 时,一元二次方程有两个相等的实数根
,相应的二次函数的图象与X轴有惟一的交点
( ,0)为二次函数的惟一的零点。
(3)当 时,一元二次方程没有实数根,相应的二
次函数的图象与X轴没有交点,二次函数没有零点。探究观察二次函数 的图象(如下图),
我们发现函数 的区间[-2,1]上有
零点,计算 与 的乘积,你能发现
这个乘积有什么特点?在区间[2,4]上是否也具有
这种特点呢?0(<或>)1 在区间[-2,1]上有零点____
2 在区间[2,4]上有零点______
____0(<或>)5-4<-35<可以发现, ,函数 在区间
(-2,1)内有零点 ,它是方程
的一个根。同样地, ,函数
在(2,4)内有零点 ,它是方程
的另一个根。同学们可以任意画几个函数图象,观察图象,看看是否能得
出同样的结果。观察下列函数 图象。1)在区间[a,b]上 (有/无)零点。
0(<或>)
2)在区间[b,c]上 (有/无)零点。
0(<或>)
3)在区间[c,d]上 (有/无)零点。
0(<或>)
有有有<<<一般地,我们有:
如果函数 在区间[a,b]上的图象是连续不
断的一条曲线,并且有 那么,函数
在区间(a,b )内有零点,即存在
使得 ,这个c也就是方程 的根。总结一下例1,求函数 的零点的个数。解:用计算机作出 的对应值表和图象。问题:
1)你可以想到什么方法来判断函数零点个数?
2)判断函数的单调性,由单调性你能得该函数的单调性具有什么特性?由表和图象可知, ,
则 ,这说明函
数在区间(2,3)内有零点。
由于函数 的定义域(0, )内是增函数,所以它仅有一个零点。随堂练习利用函数图象判断下列方程有没有根,有几个根。利用信息技术作出函数的图象,并指出下列函数零点所在的大致区间。第一课时结束!谢谢!
根与二次函数 的图象有
什么关系?思考?先观察几个具体的一元二次方程及其相应的二次函数,如:方程 与函数 方程 与函数方程 与函数(3,0)(-1,0)这样,方程 的两个实根就是函数
的图象与X轴交点的横坐标。方程 有两个根 , ;函数 的图象与x轴有两个交点
(-1,0),(3,0),如左图。方程 有两个相等的实根
函数 的图象与X轴有惟一的交点(1,0),如左图。 这样,方程
的实数根就是函数
的图象与X轴的交点的横坐标。(1,0)方程 无实数根,函数
的图象与X轴没有交点,如左图。上述关系对一般的一元二次方程
及其相应的二次函数 也成立。零点的概念对于函数 ,我们把使 的实数X叫做函数 的零点。这样,函数 的零点就是方程 的实数根,也就是函数 的图象与X轴的交点的横坐标,所以方程 有实数根 函数 有零点
函数 的图象与X轴有交点由些可知,求方程 的实数根,就是确定函数
的零点。函数零点的求法:
①(代数法)求方程 的根。②(几何法)
对于不能用求根公式的方程,可以将它与函数
的图象联系起来,并利用函数的性质找出零点. 二次函数设判别式 ,我们有:
(1)当 时,一元二次方程有两个不等的实数
根 ,相应的二次函数的图象与X轴有两个交点
( ,0),( ,0)为二次函数的两个零点。
(2)当 时,一元二次方程有两个相等的实数根
,相应的二次函数的图象与X轴有惟一的交点
( ,0)为二次函数的惟一的零点。
(3)当 时,一元二次方程没有实数根,相应的二
次函数的图象与X轴没有交点,二次函数没有零点。探究观察二次函数 的图象(如下图),
我们发现函数 的区间[-2,1]上有
零点,计算 与 的乘积,你能发现
这个乘积有什么特点?在区间[2,4]上是否也具有
这种特点呢?0(<或>)1 在区间[-2,1]上有零点____
2 在区间[2,4]上有零点______
____0(<或>)5-4<-35<可以发现, ,函数 在区间
(-2,1)内有零点 ,它是方程
的一个根。同样地, ,函数
在(2,4)内有零点 ,它是方程
的另一个根。同学们可以任意画几个函数图象,观察图象,看看是否能得
出同样的结果。观察下列函数 图象。1)在区间[a,b]上 (有/无)零点。
0(<或>)
2)在区间[b,c]上 (有/无)零点。
0(<或>)
3)在区间[c,d]上 (有/无)零点。
0(<或>)
有有有<<<一般地,我们有:
如果函数 在区间[a,b]上的图象是连续不
断的一条曲线,并且有 那么,函数
在区间(a,b )内有零点,即存在
使得 ,这个c也就是方程 的根。总结一下例1,求函数 的零点的个数。解:用计算机作出 的对应值表和图象。问题:
1)你可以想到什么方法来判断函数零点个数?
2)判断函数的单调性,由单调性你能得该函数的单调性具有什么特性?由表和图象可知, ,
则 ,这说明函
数在区间(2,3)内有零点。
由于函数 的定义域(0, )内是增函数,所以它仅有一个零点。随堂练习利用函数图象判断下列方程有没有根,有几个根。利用信息技术作出函数的图象,并指出下列函数零点所在的大致区间。第一课时结束!谢谢!
