函数的奇偶性
图片预览





文档简介
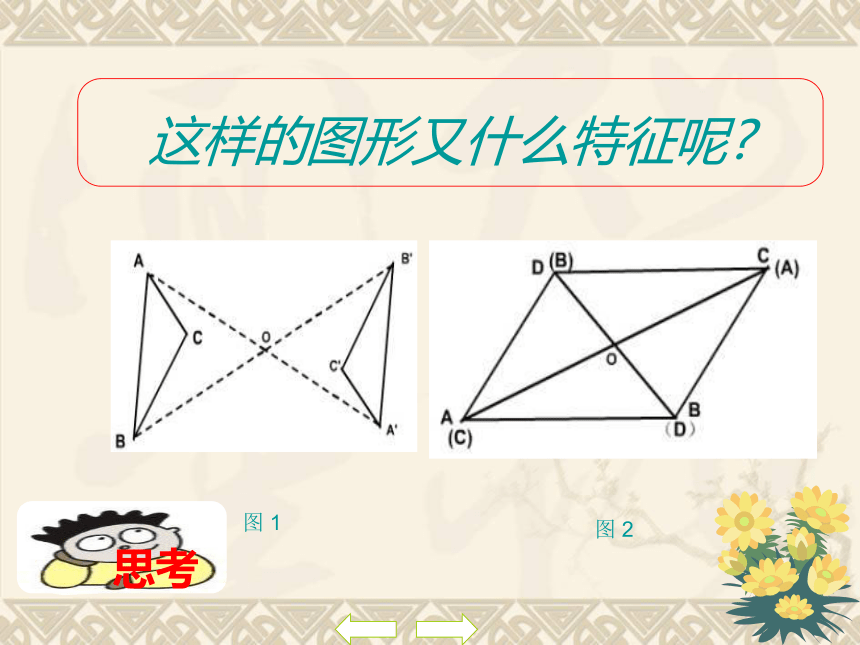
课件16张PPT。这些图案有什么特征这样的图形又什么特征呢?图 1图 2
思考函数的奇偶性函数的奇偶性奇偶函数定义及性质
奇偶函数的判断方法
课堂练习
知识归纳
本课小结
思考题
作业当 x1=1, x2=--1时,f(-1)=f(1)
当 x1=2, x2=--2时,f(-2)=f(2)当 x1=3, x2=--3时,f(-3)=f(3)对任意x,f(-x)=f(x)结论:偶函数定义:
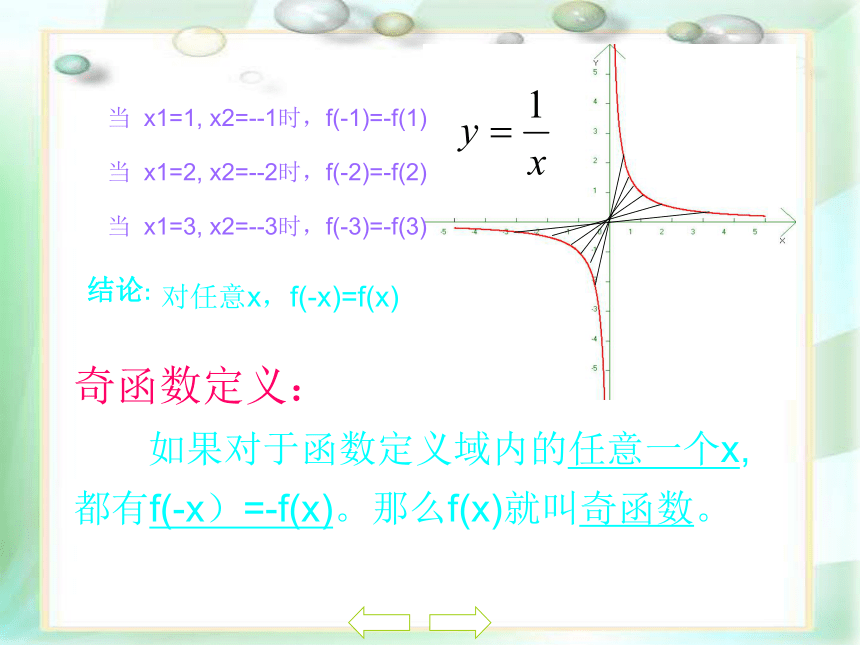
如果对于函数定义域内的任意一个x,都有f(-x)=f(x)。那么f(x)就叫偶函数。y=x2 偶函数图象的性质: 偶函数的图象在定义域内关于y轴对称.反之,如果一个函数的图象在定义域内关于y轴对称,那么这个函数是偶函数.当 x1=1, x2=--1时,f(-1)=-f(1)当 x1=2, x2=--2时,f(-2)=-f(2)当 x1=3, x2=--3时,f(-3)=-f(3)结论:对任意x,f(-x)=f(x)奇函数定义:
如果对于函数定义域内的任意一个x,都有f(-x)=-f(x)。那么f(x)就叫奇函数。
奇函数图象的性质: 奇函数的图象在定义域内关于原点称.反之,如果一个函数的图象在定义域内关于原点对称,那么这个函数是奇函数.注:如果一个函数f(x)是奇函数或偶函数,那么我们就是说函数f(x) 具有奇偶性。判断函数奇偶性的一般方法:(1)定义法: 若函数的定义域不是关于原点的对称区域,则立即判断该函数既不是奇函数也不是偶函数;若函数的定义域是关于原点的对称区间,再判断f(-x)= -f(x)或f(-x)=f(x)是否成立,也可以判断f(-x) +f(x)是否等于零等等。(2)图像法: 奇(偶)函数的充要条件是它的图像关于原点(或y轴)对称例1、判断下列函数的奇偶性(1)(2)解 (1)因为f(-x)=2x=-f(x),所以f(x)是奇函数。
(2)因为 f(-x)=|-x|-2=|x|-2=f(x),所以f(x)是偶函数。 (3) (4)(3)故f(2)不存在,所以就谈不上与f(-2)相等了,由于任意性受破坏。所以它没有奇偶性。(4)函数的定义域为[-2,2),故f(2)不存在,同上可知函
数没有奇偶性。
各抒己见解: f(x)的定义域为R
(1)当a≠0时 (2)当a=0时
∵ f(-x)=f(x)=a ∵ f(-x)=f(x)=0
∴f(x)为偶函数 f(-x)=-f(x)= 0
∴ f(x) 为既奇又偶函数 例2: 讨论函数f(x)=a(a为常数)的奇偶性注:既奇又偶的函数有且只有一类:即f(x)=0,x属于D,D关于原点对称1.用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.2.根据奇偶性, 函数可划分为四类(1)奇函数
(2)偶函数
(3)非奇非偶函数
(4)既奇又偶函数归纳:本课小结:1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称思考题? 已知f(x)是奇函数,且当x>0时,f(x)=x|x-2|,求x<0时,f(x)的表达式。作业P23 1.(1) (3) (5)
2.(2) (4) (6)
3.(2)谢谢指导!
思考函数的奇偶性函数的奇偶性奇偶函数定义及性质
奇偶函数的判断方法
课堂练习
知识归纳
本课小结
思考题
作业当 x1=1, x2=--1时,f(-1)=f(1)
当 x1=2, x2=--2时,f(-2)=f(2)当 x1=3, x2=--3时,f(-3)=f(3)对任意x,f(-x)=f(x)结论:偶函数定义:
如果对于函数定义域内的任意一个x,都有f(-x)=f(x)。那么f(x)就叫偶函数。y=x2 偶函数图象的性质: 偶函数的图象在定义域内关于y轴对称.反之,如果一个函数的图象在定义域内关于y轴对称,那么这个函数是偶函数.当 x1=1, x2=--1时,f(-1)=-f(1)当 x1=2, x2=--2时,f(-2)=-f(2)当 x1=3, x2=--3时,f(-3)=-f(3)结论:对任意x,f(-x)=f(x)奇函数定义:
如果对于函数定义域内的任意一个x,都有f(-x)=-f(x)。那么f(x)就叫奇函数。
奇函数图象的性质: 奇函数的图象在定义域内关于原点称.反之,如果一个函数的图象在定义域内关于原点对称,那么这个函数是奇函数.注:如果一个函数f(x)是奇函数或偶函数,那么我们就是说函数f(x) 具有奇偶性。判断函数奇偶性的一般方法:(1)定义法: 若函数的定义域不是关于原点的对称区域,则立即判断该函数既不是奇函数也不是偶函数;若函数的定义域是关于原点的对称区间,再判断f(-x)= -f(x)或f(-x)=f(x)是否成立,也可以判断f(-x) +f(x)是否等于零等等。(2)图像法: 奇(偶)函数的充要条件是它的图像关于原点(或y轴)对称例1、判断下列函数的奇偶性(1)(2)解 (1)因为f(-x)=2x=-f(x),所以f(x)是奇函数。
(2)因为 f(-x)=|-x|-2=|x|-2=f(x),所以f(x)是偶函数。 (3) (4)(3)故f(2)不存在,所以就谈不上与f(-2)相等了,由于任意性受破坏。所以它没有奇偶性。(4)函数的定义域为[-2,2),故f(2)不存在,同上可知函
数没有奇偶性。
各抒己见解: f(x)的定义域为R
(1)当a≠0时 (2)当a=0时
∵ f(-x)=f(x)=a ∵ f(-x)=f(x)=0
∴f(x)为偶函数 f(-x)=-f(x)= 0
∴ f(x) 为既奇又偶函数 例2: 讨论函数f(x)=a(a为常数)的奇偶性注:既奇又偶的函数有且只有一类:即f(x)=0,x属于D,D关于原点对称1.用定义判断函数奇偶性的步骤:(1)、先求定义域,看是否关于原点对称;(2)、再判断f(-x)=-f(x)或f(-x)=f(x)是否恒成立.2.根据奇偶性, 函数可划分为四类(1)奇函数
(2)偶函数
(3)非奇非偶函数
(4)既奇又偶函数归纳:本课小结:1、两个定义:对于f(x)定义域内的任意一个x,
如果都有f(-x)=-f(x) f(x)为奇函数
如果都有f(-x)=f(x) f(x)为偶函数2、两个性质:
一个函数为奇函数 它的图象关于原点对称
一个函数为偶函数 它的图象关于y轴对称思考题? 已知f(x)是奇函数,且当x>0时,f(x)=x|x-2|,求x<0时,f(x)的表达式。作业P23 1.(1) (3) (5)
2.(2) (4) (6)
3.(2)谢谢指导!
