指数函数

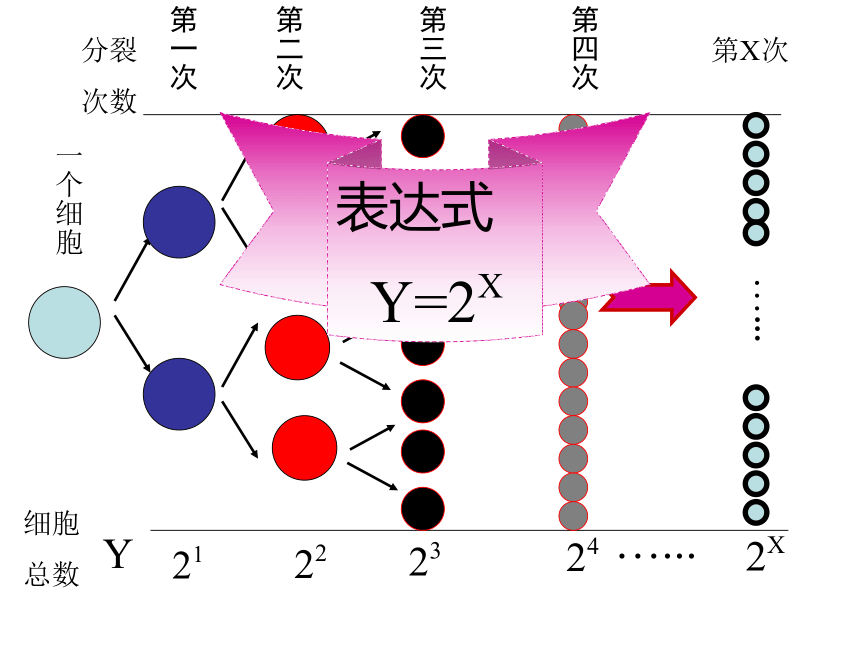
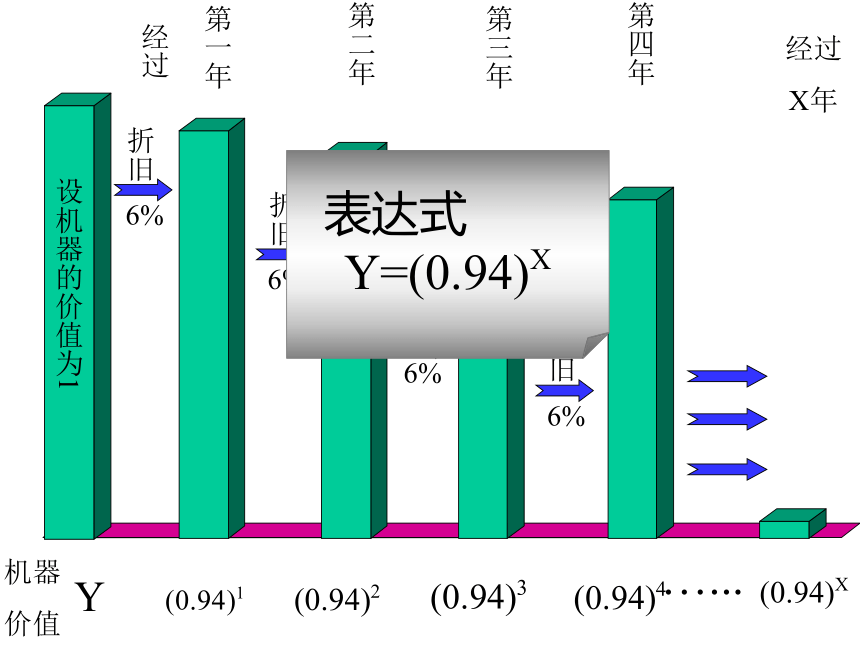
课件14张PPT。指数函数1.某种细胞分裂时,第一次由1个分裂成2个，第2次由2个分裂成4个，如此下去，如果第X次分裂得到Y个细胞，那么某细胞个数Y与次数x的函数关系是什么？2.某台机器的价值每年折旧率为6%，写出经 过X年，这台机器的价值Y与X的函数关系。思考题：指 数 函 数分裂
次数第一次第二次第三次第四次第X次…...经过第一年第二年第三年第四年经过
X年…...设问2:y=ax (a>0且a≠1) ,当X取全体实数
对y=ax 中的底 数为什么要求(a>0且a≠1)?方法:可举几个“特例”,看一看a为何值时, X不能取全体实数?a为何值时,X可取全体实数?不能取全体实数的将不研究.小实验：a的范围这就是我们要学习的指数函数:y=ax (a>0且a≠1)设问1: 象 y=2x和y=(0.94)x的函数是什么函数,它的一般式是什么?当a>0时,
当a=1时,
当a=0时,若x>0 则
若x≤0 则
当a<0时，

为了便于研究，规定：a>0 且a≠1y=ax 中a的范围：ax有意义，无研究价值提问： 那么什么是指数函数呢？思考后回答？a的取值a<0a>001设问3：我们研究函数的性质，通常通过函数图象
来研究函数的哪几个性质？设问4：那么得到函数的图象一般用什么方法？列表、求对应的x和y值、描点、作图答: 1.定义域 2.值域 3.单调性 4.对称性等············因为2>1 所以y=2x与y=ax(a>1)的图象相似由此可知y=ax 的性质y=2xy=2x 1 y=ax (a>0且a≠1) 的定义域为:R y=ax (a>0且a≠1) 的值域为：R+ y=ax (a>1)在整个定义域上是单调递增的
而y=ax (1>a>0)在整个定义域上是单调递减的y=ax (a>1) 和y=ax(01)都过点(0,1) 并且
⑴a>1: 当x>0时y>1;当x<0,y∈(0,1)
⑵1>a>0: 当x>0, y∈(0,1);当x<0,y∈(1,+∞)
y=ax和 y=a-x的图象关于轴对称1.定义域: 2. 值域:3.单调性:4.特殊点: 5.对称性:注意：请同学们自己将函数的图象和性质总结并列成表我们根据y=2x和y=( )x的图象来研究y=ax (a>0且a≠1)的性质 现在通过指数函数图象来研究其性质思考题: 比较大小(1) 1.012.7和1.013.5
(2) 0.993.3和0.994.5点滴收获：
1. 本节课学习了那些知识?指数函数的定义2.如何记忆函数的性质?指数函数的图象及性质数形结合的方法记忆3.记住两个基本图形:谢谢指导！