2015-2016学年人教版九年级数学上册21.2.1 解一元二次方程(配方法)
文档属性
| 名称 | 2015-2016学年人教版九年级数学上册21.2.1 解一元二次方程(配方法) |

|
|
| 格式 | zip | ||
| 文件大小 | 138.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-05 00:00:00 | ||
图片预览








文档简介
课件22张PPT。人教版九年级数学上册同步授课课件21.2 解一元二次方程21.2.1 配方法21.2 解一元二次方程 1.掌握用配方法解一元二次方程的一般步骤.2.学会利用配方法解一元二次方程.3.通过配方法的探究活动,培养学生勇于探索的良好学习习惯.用配方法熟练地解数字系数为1的一元二次方程.用配方法解二次项系数不是1的一元二次方程,首先方程两边都除以二次项系数,将方程化为二次项系数是1的类型.21.2 解一元二次方程1.通过配成________________来解一元二次方程的方法叫做配方法.
2.配方法的一般步骤:
(1)化二次项系数为1,并将含有未知数的项放在方程的左边,常数项放在方程的右边;
(2)配方:方程两边同时加上_______________________,使左边配成一个完全平方式,写成________________的形式;
(3)若p________0,则可直接开平方求出方程的解;若p_______0,则方程无解.21.2 解一元二次方程完全平方形式一次项系数的一半的平方(mx+n)2=p≥<21.2 解一元二次方程自主检测1.下列二次三项式是完全平方式的是( )
A.x2-8x-16 B.x2+8x+16
C.x2-4x-16 D.x2+4x+16
2.若x2-6x+m2是一个完全平方式,则m的值是( )
A.3 B.-3
C.±3 D.以上都不对
3.用适当的数填空:B x2-4x+_____=(x-_____)2;
m2_____m+ =(m_____)2.C 4 2 21.2 解一元二次方程1.完成下列配方过程.16 4 2.解方程: x2+6x+7=0讨论梳理21.2 解一元二次方程讨论梳理1.解方程的方法你知道是什么了吗?它里面蕴含着非常重要的数学思想,你知道是什么了吗?配方 降次2.那你知道用这种方法解方程时最关键的一步是什么了吗?你能说说你发现了什么没有?方程两边都加上一次项系数的一半的平方,使左边配成一个完全平方式3.你能总结出来用这种方法解一元二次方程的步骤吗?21.2 解一元二次方程讨论梳理(1)把常数项移到方程右边;
(2)方程两边同除以二次项系数,化二次项系数为1;
(3)方程两边都加上一次项系数一半的平方;
(4)原方程变形为(x+m)2=n的形式;
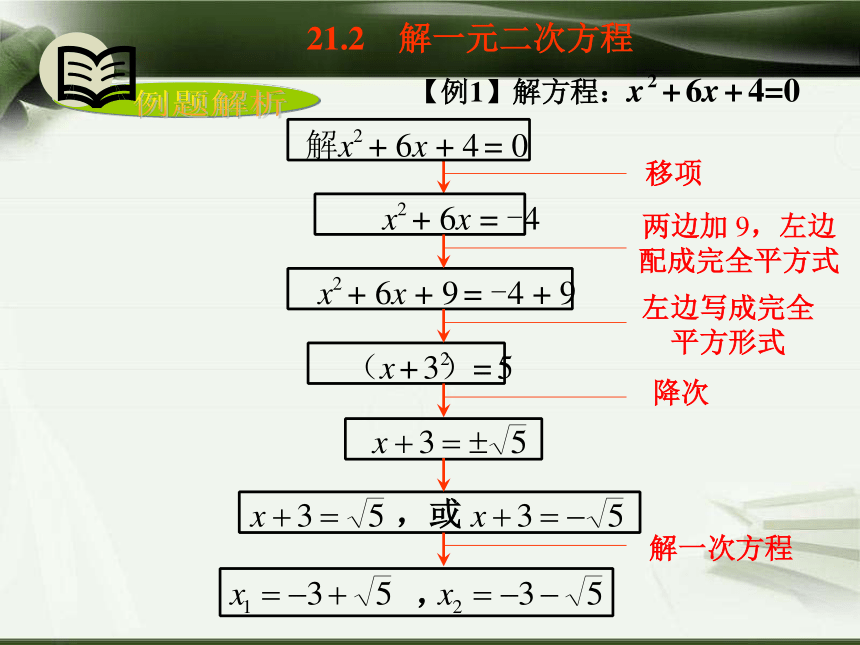
(5)如果右边是非负数,就可以直接开平方求出方程的解,如果右边是负数,则一元二次方程无解.3.你能总结出来用这种方法解一元二次方程的步骤吗?【例1】解方程:x 2 + 6x + 4=0 21.2 解一元二次方程两边加 9,左边 配成完全平方式 移项左边写成完全 平方形式 降次解一次方程解x2 + 6x + 4 = 0x2 + 6x = -4x2 + 6x + 9 = -4 + 9,或,【例2】用配方法解方程:3x2+8x-3=021.2 解一元二次方程解:两边除以3,得:移项,得:配方,得:即:开方,得:分析:配方法解一元二次方程的一般步骤:
(1)把二次项的系数化为1;
(2)把常数项移到等号的右边;
(3)等式两边同时加上一次项系数一半的平方.
(4)用直接开平方法解这个方程.21.2 解一元二次方程例题解析【例3】 当x,y取何值时,多项式x2+4x+4y2﹣4y+1取得最小值,并求出最小值.解:x2+4x+4y2﹣4y+1=x2+4x+4+4y2﹣4y+1﹣4
=(x+2)2+(2y﹣1)2﹣4,
又∵(x+2)2+(2y﹣1)2的最小值是0,
∴x2+4x+4y2﹣4y+1的最小值为﹣4.
∴当x=﹣2,y= 时有最小值为﹣4.解析:配方法是求代数式的最值问题中最常用的方法.基本思路是:把代数式配方成完全平方式与常数项的和,根据完全平方式的非负性求代数式的最值.21.2 解一元二次方程1.用配方法解一元二次方程x2-4x=5时,此方程可变形为( )
A.(x+2)2=1 B.(x-2)2=1
C.(x+2)2=9 D.(x-2)2=9
2.下列配方有错误的是( )
A.x2-2x-3=0化为(x-1)2=4
B.x2+6x+8=0化为(x+3)2=1
C.x2-4x-1=0化为(x-2)2=5
D.x2-2x-124=0化为(x-1)2=124D D 21.2 解一元二次方程C D 21.2 解一元二次方程B B B 21.2 解一元二次方程解:(1)4.用配方法解方程:(1)x2-4x+2=0
(2)x2+6x-5=0解:(2)21.2 解一元二次方程解(1):5.用配方法解方程:(1)3x2-6x-3=0
(2)2x2-5x-4=0解:(2)请谈谈你的收获小组合作讨论21.2 解一元二次方程21.2 解一元二次方程1.用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )
A.(x-1)2=4 B.(x+1)2=4
C.(x-1)2=16 D.(x+1)2=16
2.一个小球以15 m/s的初速度向上竖直弹出,它在空中的高度h(m)与时间t(s)满足关系式h=15t-5t2,当小球的高度为10 m时,t为( )
A.1 s B.2 s
C.1 s或2 s D.不能确定
A C 21.2 解一元二次方程C D 21.2 解一元二次方程5.已知A=a+2,B=a2-a+5,C=a2+5a+19.
(1)求证:B-A>0;
(2)指出A与C哪个大?并说明理由.解:(1)B-A=(a-1)2+2>0
(2)C-A=(a+2)2+13>0,∴C>A6.试证明关于x的方程(a2-8a+20)x2+2ax+1=0,无论a为何值,该方程都是一元二次方程.解:∵a2-8a+20=(a-4)2+4≠0,
∴无论a取何值,该方程都是一元二次方程
21.2 解一元二次方程1.(吉林中考)若将方程x2+6x=7化为(x+m)2=16,则m=______.2.(兰州中考)用配方法解方程x2-2x-1=0时,配方后得的方程为( ).
A.(x+1)2=0 B.(x-1)2=0
C.(x+1)2=2 D.(x-1)2=23 D 21.2 解一元二次方程3.(葫芦岛中考)有n个方程:x2+2x-8=0;
x2+2×2x-8×22=0;……;x2+2nx-8n2=0.
小静同学解第1个方程x2+2x-8=0的步骤为:“①x2+2x=8;②x2+2x+1=8+1;③(x+1)2=9;④x+1=±3;⑤x=1±3;⑥x1=4,x2=-2.”
(1)小静的解法是从步骤______开始出现错误的;
(2)用配方法解第n个方程x2+2nx-8n2=0.(用含n的式子表示方程的根)⑤解:(2)x2+2nx-8n2=0,x2+2nx=8n2,x2+2nx+n2=8n2+n2,(x+n)2=9n2, x+n=±3n,x=-n±3n, ∴x1=-4n,x2=2n.21.2 解一元二次方程再见
2.配方法的一般步骤:
(1)化二次项系数为1,并将含有未知数的项放在方程的左边,常数项放在方程的右边;
(2)配方:方程两边同时加上_______________________,使左边配成一个完全平方式,写成________________的形式;
(3)若p________0,则可直接开平方求出方程的解;若p_______0,则方程无解.21.2 解一元二次方程完全平方形式一次项系数的一半的平方(mx+n)2=p≥<21.2 解一元二次方程自主检测1.下列二次三项式是完全平方式的是( )
A.x2-8x-16 B.x2+8x+16
C.x2-4x-16 D.x2+4x+16
2.若x2-6x+m2是一个完全平方式,则m的值是( )
A.3 B.-3
C.±3 D.以上都不对
3.用适当的数填空:B x2-4x+_____=(x-_____)2;
m2_____m+ =(m_____)2.C 4 2 21.2 解一元二次方程1.完成下列配方过程.16 4 2.解方程: x2+6x+7=0讨论梳理21.2 解一元二次方程讨论梳理1.解方程的方法你知道是什么了吗?它里面蕴含着非常重要的数学思想,你知道是什么了吗?配方 降次2.那你知道用这种方法解方程时最关键的一步是什么了吗?你能说说你发现了什么没有?方程两边都加上一次项系数的一半的平方,使左边配成一个完全平方式3.你能总结出来用这种方法解一元二次方程的步骤吗?21.2 解一元二次方程讨论梳理(1)把常数项移到方程右边;
(2)方程两边同除以二次项系数,化二次项系数为1;
(3)方程两边都加上一次项系数一半的平方;
(4)原方程变形为(x+m)2=n的形式;
(5)如果右边是非负数,就可以直接开平方求出方程的解,如果右边是负数,则一元二次方程无解.3.你能总结出来用这种方法解一元二次方程的步骤吗?【例1】解方程:x 2 + 6x + 4=0 21.2 解一元二次方程两边加 9,左边 配成完全平方式 移项左边写成完全 平方形式 降次解一次方程解x2 + 6x + 4 = 0x2 + 6x = -4x2 + 6x + 9 = -4 + 9,或,【例2】用配方法解方程:3x2+8x-3=021.2 解一元二次方程解:两边除以3,得:移项,得:配方,得:即:开方,得:分析:配方法解一元二次方程的一般步骤:
(1)把二次项的系数化为1;
(2)把常数项移到等号的右边;
(3)等式两边同时加上一次项系数一半的平方.
(4)用直接开平方法解这个方程.21.2 解一元二次方程例题解析【例3】 当x,y取何值时,多项式x2+4x+4y2﹣4y+1取得最小值,并求出最小值.解:x2+4x+4y2﹣4y+1=x2+4x+4+4y2﹣4y+1﹣4
=(x+2)2+(2y﹣1)2﹣4,
又∵(x+2)2+(2y﹣1)2的最小值是0,
∴x2+4x+4y2﹣4y+1的最小值为﹣4.
∴当x=﹣2,y= 时有最小值为﹣4.解析:配方法是求代数式的最值问题中最常用的方法.基本思路是:把代数式配方成完全平方式与常数项的和,根据完全平方式的非负性求代数式的最值.21.2 解一元二次方程1.用配方法解一元二次方程x2-4x=5时,此方程可变形为( )
A.(x+2)2=1 B.(x-2)2=1
C.(x+2)2=9 D.(x-2)2=9
2.下列配方有错误的是( )
A.x2-2x-3=0化为(x-1)2=4
B.x2+6x+8=0化为(x+3)2=1
C.x2-4x-1=0化为(x-2)2=5
D.x2-2x-124=0化为(x-1)2=124D D 21.2 解一元二次方程C D 21.2 解一元二次方程B B B 21.2 解一元二次方程解:(1)4.用配方法解方程:(1)x2-4x+2=0
(2)x2+6x-5=0解:(2)21.2 解一元二次方程解(1):5.用配方法解方程:(1)3x2-6x-3=0
(2)2x2-5x-4=0解:(2)请谈谈你的收获小组合作讨论21.2 解一元二次方程21.2 解一元二次方程1.用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是( )
A.(x-1)2=4 B.(x+1)2=4
C.(x-1)2=16 D.(x+1)2=16
2.一个小球以15 m/s的初速度向上竖直弹出,它在空中的高度h(m)与时间t(s)满足关系式h=15t-5t2,当小球的高度为10 m时,t为( )
A.1 s B.2 s
C.1 s或2 s D.不能确定
A C 21.2 解一元二次方程C D 21.2 解一元二次方程5.已知A=a+2,B=a2-a+5,C=a2+5a+19.
(1)求证:B-A>0;
(2)指出A与C哪个大?并说明理由.解:(1)B-A=(a-1)2+2>0
(2)C-A=(a+2)2+13>0,∴C>A6.试证明关于x的方程(a2-8a+20)x2+2ax+1=0,无论a为何值,该方程都是一元二次方程.解:∵a2-8a+20=(a-4)2+4≠0,
∴无论a取何值,该方程都是一元二次方程
21.2 解一元二次方程1.(吉林中考)若将方程x2+6x=7化为(x+m)2=16,则m=______.2.(兰州中考)用配方法解方程x2-2x-1=0时,配方后得的方程为( ).
A.(x+1)2=0 B.(x-1)2=0
C.(x+1)2=2 D.(x-1)2=23 D 21.2 解一元二次方程3.(葫芦岛中考)有n个方程:x2+2x-8=0;
x2+2×2x-8×22=0;……;x2+2nx-8n2=0.
小静同学解第1个方程x2+2x-8=0的步骤为:“①x2+2x=8;②x2+2x+1=8+1;③(x+1)2=9;④x+1=±3;⑤x=1±3;⑥x1=4,x2=-2.”
(1)小静的解法是从步骤______开始出现错误的;
(2)用配方法解第n个方程x2+2nx-8n2=0.(用含n的式子表示方程的根)⑤解:(2)x2+2nx-8n2=0,x2+2nx=8n2,x2+2nx+n2=8n2+n2,(x+n)2=9n2, x+n=±3n,x=-n±3n, ∴x1=-4n,x2=2n.21.2 解一元二次方程再见
同课章节目录
