第13章 轴对称 单元测试卷(含答案)2024-—2025学年人教版数学八年级上册
文档属性
| 名称 | 第13章 轴对称 单元测试卷(含答案)2024-—2025学年人教版数学八年级上册 | 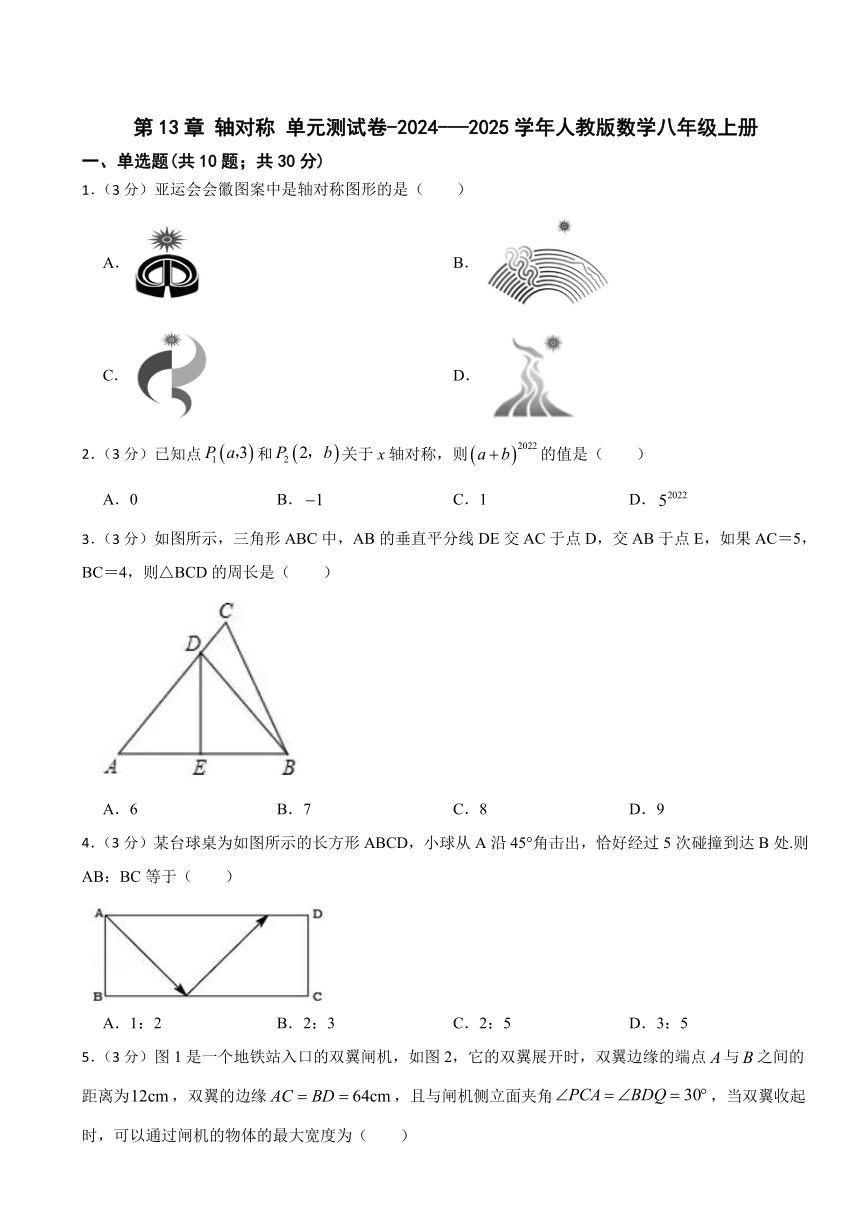 | |
| 格式 | docx | ||
| 文件大小 | 899.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-30 09:07:47 | ||
图片预览




文档简介
第13章 轴对称 单元测试卷-2024-—2025学年人教版数学八年级上册
一、单选题(共10题;共30分)
1.(3分)亚运会会徽图案中是轴对称图形的是( )
A. B.
C. D.
2.(3分)已知点和关于x轴对称,则的值是( )
A.0 B. C.1 D.
3.(3分)如图所示,三角形ABC中,AB的垂直平分线DE交AC于点D,交AB于点E,如果AC=5,BC=4,则△BCD的周长是( )
A.6 B.7 C.8 D.9
4.(3分)某台球桌为如图所示的长方形ABCD,小球从A沿45°角击出,恰好经过5次碰撞到达B处.则AB:BC等于( )
A.1:2 B.2:3 C.2:5 D.3:5
5.(3分)图1是一个地铁站入口的双翼闸机,如图2,它的双翼展开时,双翼边缘的端点与之间的距离为,双翼的边缘,且与闸机侧立面夹角,当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. B. C. D.
6.(3分)如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为 ( )
A.30° B.45° C.50° D.75°
7.(3分)如图,,,,分别平分的内角,外角,外角.以下结论:①;②;③;④和都是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)已知,在△ABC中,,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是( )
A. B.△BCD是等边三角形
C.AD垂直平分BC D.
9.(3分)在平面直角坐标系中,已知点A(﹣1,1),B(﹣3,2),点C在坐标轴上,若△ABC是等腰三角形,则满足条件的点C的个数是( )
A.4个 B.5个 C.7个 D.8个
10.(3分)如图,在四边形中,,,我们把这种两组邻边分别相等的四边形叫做“筝形”,筝形的对角线、相交于点.已知,,小婵同学得到如下结论:①是等边三角形;②;③;④点、分别在线段、上,且,则,其中正确的结论有( )
A.个 B.个 C.个 D.个
二、填空题(共6题;共18分)
11.(3分)已知点在反比例函数的图象上,点在轴正半轴上,若为等腰直角三角形,则的长为 .
12.(3分)如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,有以下的几种说法:①AM=BM;②∠MAP=∠MBP;③∠ANM=∠BNM;④AP=BN;⑤△AMP≌△BMP.其中正确的说法是 .(填序号)
13.(3分)如图,OA,OB分别是线段MC、MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发,爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径的长度为 .
14.(3分)如图,在中,,,,,的长是 .
15.(3分)等腰三角形的两边长分别为和,则这个三角形的周长为 .
16.(3分)如图,在中,,,于点D,平分交于点E,交于点G,过点A作于点H,交于点F,下列结论:①;②;③;④,其中正确的序号有 .
三、综合题(共6题;共52分)
17.(6分)如图,在△ABC中,∠A>∠B.
(1)(3分)作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);
(2)(3分)在(1)的条件下,连接AE,若∠B=50°,求∠AEC的度数.
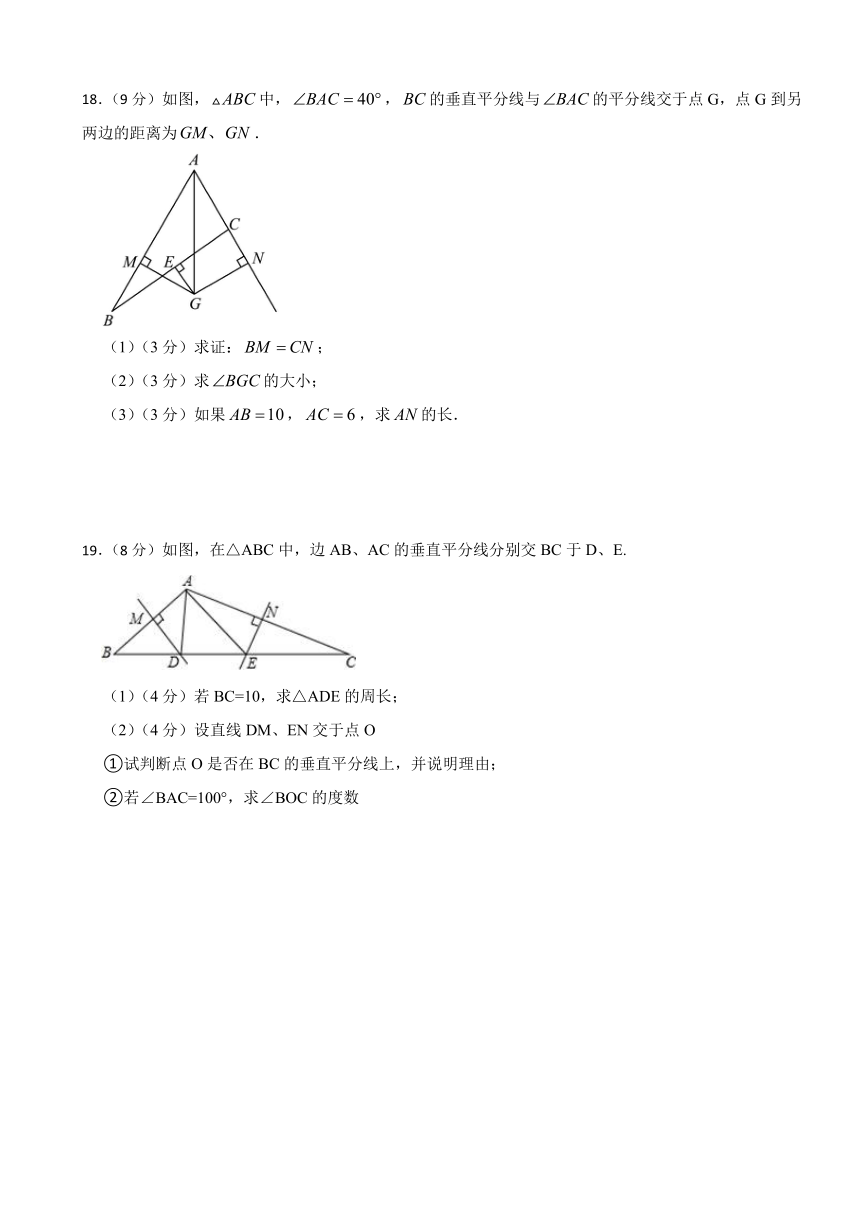
18.(9分)如图,中,,的垂直平分线与的平分线交于点G,点G到另两边的距离为.
(1)(3分)求证:;
(2)(3分)求的大小;
(3)(3分)如果,,求的长.
19.(8分)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)(4分)若BC=10,求△ADE的周长;
(2)(4分)设直线DM、EN交于点O
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数
20.(8分)如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)(4分)求证:OE是CD的垂直平分线.
(2)(4分)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
21.(9分)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)(3分)求证:△ABD≌△BCE;
(2)(3分)求证:AC是线段ED的垂直平分线.
(3)(3分)△DBC是等腰三角形吗?请说明理由.
22.(12分)如图,在正方形网格中,每个小正方形的边长都是1个单位长度,的三个顶点都在格点上.
(1)(3分)画出关于成轴对称的;
(2)(3分)在直线上找一点,使的周长最小,请用画图的方法确定点的位置,并直接写出周长的最小值为 ▲ .
(3)(3分)若在直线上存在一点,使是等腰三角形,则这样的点有 个.
(4)(3分)若点也在格点上(不与点重合),且与全等,在图上画出符合条件的点,并分别写出每个与的位置关系: ▲ .
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】C
11.【答案】或
12.【答案】①②③⑤
13.【答案】10cm
14.【答案】18
15.【答案】
16.【答案】①③④
17.【答案】(1)解:如图所示;
(2)解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠EAB=∠B=50°,
∴∠AEC=∠EAB+∠B=100°.
18.【答案】(1)证明:连接,如图所示:
∵平分,,,
∴,
∵垂直平分于点E,
∴,
在和中,
,
∴,
∴;
(2)解:∵,,
∴
∵,
∴,
∵,
∴,
∴;
(3)解:根据(1)知,,
在和中
,
∴,
∴,
∴,
∴
∴
19.【答案】(1)∵在△ABC中,AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE,
又∵BC=10,
∴△ADE周长为:AD+DE+AE=BD+DE+EC=BC=10
(2)①如图,连接OB,OA,OC,
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴BO=AO,CO=AO,
∴BO=CO,
∴O在BC的垂直平分线上;
②∵OM⊥AB,ON⊥AC,
∴∠AMO=∠ANO=90°,
∵∠BAC=100°,
∴∠MOM=360°-∠AMO-∠BAC-∠ANO=80°;
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴∠BOM=∠AOM,∠CON=∠AON,
∴∠BOC=2∠MON=160°.
20.【答案】(1)证明:∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,又∵OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
又∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)解:∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵ED⊥OA,CD⊥OE,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
21.【答案】(1)解:如图证明:∵∠ABC=90°,BD⊥EC,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△BAD和△CBE中,
,
∴△BAD≌△CBE(ASA),
(2)证明:∵E是AB中点,
∴EB=EA,
∵AD=BE,
∴AE=AD,
∵AD∥BC,
∴∠7=∠ACB=45°,
∵∠6=45°,
∴∠6=∠7,
又∵AD=AE,
∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线;
(3)解:△DBC是等腰三角形(CD=BD).
理由如下:
∵由(2)得:CD=CE,由(1)得:CE=BD,
∴CD=BD.
∴△DBC是等腰三角形.
22.【答案】(1)解:如图所示,即为所求;
(2)解:如图,作点A关于的对称点,连接与的交点即为所求点P.
;
(3)2
(4)解:如图所示,
;
与关于所在直线成轴对称,
与关于的中垂线成轴对称,
与关于的中点成中心对称.
一、单选题(共10题;共30分)
1.(3分)亚运会会徽图案中是轴对称图形的是( )
A. B.
C. D.
2.(3分)已知点和关于x轴对称,则的值是( )
A.0 B. C.1 D.
3.(3分)如图所示,三角形ABC中,AB的垂直平分线DE交AC于点D,交AB于点E,如果AC=5,BC=4,则△BCD的周长是( )
A.6 B.7 C.8 D.9
4.(3分)某台球桌为如图所示的长方形ABCD,小球从A沿45°角击出,恰好经过5次碰撞到达B处.则AB:BC等于( )
A.1:2 B.2:3 C.2:5 D.3:5
5.(3分)图1是一个地铁站入口的双翼闸机,如图2,它的双翼展开时,双翼边缘的端点与之间的距离为,双翼的边缘,且与闸机侧立面夹角,当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. B. C. D.
6.(3分)如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为 ( )
A.30° B.45° C.50° D.75°
7.(3分)如图,,,,分别平分的内角,外角,外角.以下结论:①;②;③;④和都是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)已知,在△ABC中,,如图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D; (2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中错误的是( )
A. B.△BCD是等边三角形
C.AD垂直平分BC D.
9.(3分)在平面直角坐标系中,已知点A(﹣1,1),B(﹣3,2),点C在坐标轴上,若△ABC是等腰三角形,则满足条件的点C的个数是( )
A.4个 B.5个 C.7个 D.8个
10.(3分)如图,在四边形中,,,我们把这种两组邻边分别相等的四边形叫做“筝形”,筝形的对角线、相交于点.已知,,小婵同学得到如下结论:①是等边三角形;②;③;④点、分别在线段、上,且,则,其中正确的结论有( )
A.个 B.个 C.个 D.个
二、填空题(共6题;共18分)
11.(3分)已知点在反比例函数的图象上,点在轴正半轴上,若为等腰直角三角形,则的长为 .
12.(3分)如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,有以下的几种说法:①AM=BM;②∠MAP=∠MBP;③∠ANM=∠BNM;④AP=BN;⑤△AMP≌△BMP.其中正确的说法是 .(填序号)
13.(3分)如图,OA,OB分别是线段MC、MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发,爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点,则小蚂蚁爬行的最短路径的长度为 .
14.(3分)如图,在中,,,,,的长是 .
15.(3分)等腰三角形的两边长分别为和,则这个三角形的周长为 .
16.(3分)如图,在中,,,于点D,平分交于点E,交于点G,过点A作于点H,交于点F,下列结论:①;②;③;④,其中正确的序号有 .
三、综合题(共6题;共52分)
17.(6分)如图,在△ABC中,∠A>∠B.
(1)(3分)作边AB的垂直平分线DE,与AB,BC分别相交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);
(2)(3分)在(1)的条件下,连接AE,若∠B=50°,求∠AEC的度数.
18.(9分)如图,中,,的垂直平分线与的平分线交于点G,点G到另两边的距离为.
(1)(3分)求证:;
(2)(3分)求的大小;
(3)(3分)如果,,求的长.
19.(8分)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)(4分)若BC=10,求△ADE的周长;
(2)(4分)设直线DM、EN交于点O
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数
20.(8分)如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)(4分)求证:OE是CD的垂直平分线.
(2)(4分)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
21.(9分)如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)(3分)求证:△ABD≌△BCE;
(2)(3分)求证:AC是线段ED的垂直平分线.
(3)(3分)△DBC是等腰三角形吗?请说明理由.
22.(12分)如图,在正方形网格中,每个小正方形的边长都是1个单位长度,的三个顶点都在格点上.
(1)(3分)画出关于成轴对称的;
(2)(3分)在直线上找一点,使的周长最小,请用画图的方法确定点的位置,并直接写出周长的最小值为 ▲ .
(3)(3分)若在直线上存在一点,使是等腰三角形,则这样的点有 个.
(4)(3分)若点也在格点上(不与点重合),且与全等,在图上画出符合条件的点,并分别写出每个与的位置关系: ▲ .
答案解析部分
1.【答案】A
2.【答案】C
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】D
8.【答案】D
9.【答案】C
10.【答案】C
11.【答案】或
12.【答案】①②③⑤
13.【答案】10cm
14.【答案】18
15.【答案】
16.【答案】①③④
17.【答案】(1)解:如图所示;
(2)解:∵DE是AB的垂直平分线,
∴AE=BE,
∴∠EAB=∠B=50°,
∴∠AEC=∠EAB+∠B=100°.
18.【答案】(1)证明:连接,如图所示:
∵平分,,,
∴,
∵垂直平分于点E,
∴,
在和中,
,
∴,
∴;
(2)解:∵,,
∴
∵,
∴,
∵,
∴,
∴;
(3)解:根据(1)知,,
在和中
,
∴,
∴,
∴,
∴
∴
19.【答案】(1)∵在△ABC中,AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE,
又∵BC=10,
∴△ADE周长为:AD+DE+AE=BD+DE+EC=BC=10
(2)①如图,连接OB,OA,OC,
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴BO=AO,CO=AO,
∴BO=CO,
∴O在BC的垂直平分线上;
②∵OM⊥AB,ON⊥AC,
∴∠AMO=∠ANO=90°,
∵∠BAC=100°,
∴∠MOM=360°-∠AMO-∠BAC-∠ANO=80°;
∵MO是AB的垂直平分线,NO是AC的垂直平分线,
∴∠BOM=∠AOM,∠CON=∠AON,
∴∠BOC=2∠MON=160°.
20.【答案】(1)证明:∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,
∴DE=CE,又∵OE=OE,
∴Rt△ODE≌Rt△OCE,
∴OD=OC,
∴△DOC是等腰三角形,
又∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线;
(2)解:∵OE是∠AOB的平分线,∠AOB=60°,
∴∠AOE=∠BOE=30°,
∵ED⊥OA,CD⊥OE,
∴OE=2DE,∠ODF=∠OED=60°,
∴∠EDF=30°,
∴DE=2EF,
∴OE=4EF.
21.【答案】(1)解:如图证明:∵∠ABC=90°,BD⊥EC,
∴∠1+∠3=90°,∠2+∠3=90°,
∴∠1=∠2,
在△BAD和△CBE中,
,
∴△BAD≌△CBE(ASA),
(2)证明:∵E是AB中点,
∴EB=EA,
∵AD=BE,
∴AE=AD,
∵AD∥BC,
∴∠7=∠ACB=45°,
∵∠6=45°,
∴∠6=∠7,
又∵AD=AE,
∴AM⊥DE,且EM=DM,
即AC是线段ED的垂直平分线;
(3)解:△DBC是等腰三角形(CD=BD).
理由如下:
∵由(2)得:CD=CE,由(1)得:CE=BD,
∴CD=BD.
∴△DBC是等腰三角形.
22.【答案】(1)解:如图所示,即为所求;
(2)解:如图,作点A关于的对称点,连接与的交点即为所求点P.
;
(3)2
(4)解:如图所示,
;
与关于所在直线成轴对称,
与关于的中垂线成轴对称,
与关于的中点成中心对称.
