函数的奇偶性

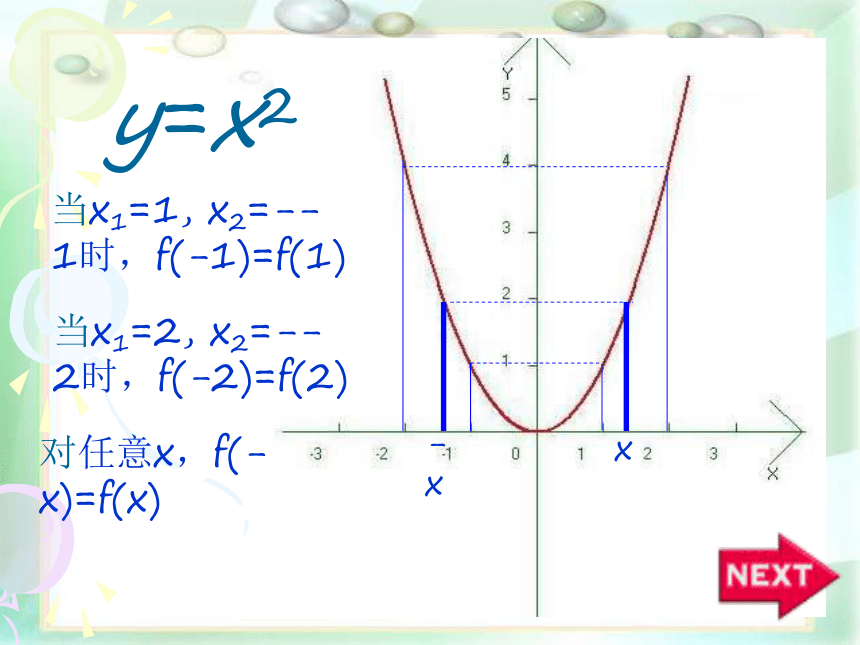
课件12张PPT。函数的奇偶性y=x2 -xx当x1=1, x2=--1时，f(-1)=f(1)
当x1=2, x2=--2时，f(-2)=f(2)
对任意x，f(-x)=f(x)
偶函数定义：如果对于函数定义域内的任意一个x,都有f(-x）=f(x)。那么f(x)就叫偶函数。奇函数定义：如果对于函数定义域内的任意一个x,都有f(-x）=-f(x)。那么f(x)就叫奇函数。例1、判断下列函数的奇偶性（3）解：(1) 因为f(-x)=2x=-f(x),所 以f(x)是奇函数。
因为 f(-x)=|-x|-2=|x|-2=f(x),所以f(x)是偶函数。
因为是偶函数。（1） （2）判断奇偶性，只需验证f(x)与f(-x)之间的关系。（5）（6）（4） 定义域关于原点对称是函数具有奇偶性的必要但不充分条件。故f(2)不存在，所以就谈不上与f(-2)相等了，由于任意性受破坏。所以它没有奇偶性。解：（4） （5）函数的定义域为[-2,2),故f(2)不存在，同上可知函数没有奇偶性。（6）故函数没有奇偶性。思考：在刚才的几个函数中有的是奇函数不是偶函数，有的是偶函数不是奇函数，也有既不是奇函数也不是偶函数的。那么有没有这样的函数，它既是奇函数又是偶函数呢？f(x)=0是不是具备这样性质的函数解析式只能写成这样呢？例2、已知函数f(x)既是奇函数又是偶函数。求证：f(x)=0证明：因为 f(x)既是奇函数又是偶函数
所以f(-x)=f(x),且f(-x)=-f(x)
所以f(x)= -f(x)
所以2f(x)=0
即f(x)=0.这样的函数有多少个呢？函数按是否有奇偶性可分为四类：奇函数
偶函数
既是奇函数又是偶函数
既不是奇函数又不是偶函数例3、判断下列函数的奇偶性1、解：当b=0时，f(x)为奇函数，当b 0时，f(x)既不是奇函数，也不是偶函数。2、解：当a=0时，f(x)既是奇函数又是偶函数，当a 0时，f(x)是偶函数。小结：奇偶性的概念
判断奇偶性时要注意的问题再见