简谐运动的多解性与机械波传播问题的多解性--2025高考物理热点模型(PDF版,含解析)
文档属性
| 名称 | 简谐运动的多解性与机械波传播问题的多解性--2025高考物理热点模型(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-10-30 07:56:49 | ||
图片预览



文档简介
简谐运动的多解性与机械波传播问题的多解性--2025
高考物理热点模型含答案
简谐运动的多解性与机械波传播的多解性问题
学校:_________班级:___________姓名:_____________
01 模型概述
1.简谐运动的周期性与对称性
1)周期性
①相隔Δt= n+ 1 T(n= 0,1,2,3 )的两个时刻,弹簧振子的位置关于平衡位置对称,位移等大反2
向 (或都为零),速度等大反向 (或都为零),加速度等大反向 (或都为零).
②相隔Δt=nT(n= 0,1,2,3 )的两个时刻,弹簧振子在同一位置,位移、速度和加速度都相同.
2)对称性
关于平衡位置O对称的两点,速度的大小、动能、势能、相对平衡位置的位移大小相等,由对称点向平衡
位置O运动时用时相等
2.波传播问题的多解性问题及分析思路
1)造成造成波传播问题多解的主要因素
①周期性
a)时间周期性:时间间隔Δt与周期T的关系不明确.
b)空间周期性:波传播的距离Δx与波长 λ的关系不明确.
②双向性
a)传播方向双向性:波的传播方向不确定.
b)振动方向双向性:质点振动方向不确定.
2)解决波的多解问题的思路
①首先考虑传播方向的双向性:如果题目未说明波的传播方向或没有其他条件暗示,应首先按波传播方
向的可能性进行讨论。
②对设定的传播方向:机械波在一个周期内不同时刻图像的形状是不同的,但在相隔时间为周期整数倍
的不同时刻图像的形状则是相同的,这种周期性必然导致波的传播距离、时间和速度等物理量有多个值与之对
应。
一般采用从特殊到一般的思维方法,先确定最简单的情况,即先找出一个周期 (或一个波长内)内满足
条件的关系Δt或Δx,然后在此基础上加 nT(或nλ)。若此关系为时间,则 t=nT+Δt(n= 0,1,2,3, );若
此关系为距离,则x= nλ+Δx( = x nλ+Δxn 0,1,2,3, ).最后求速度 v= = ,其中 n= 0,1,2, 且 k
t kT+Δt
= 0,1,2, )。
1
02 典题攻破
1.简谐运动的多解性问题
1. (2024·陕西西安·模拟预测) (多选)如图所示,弹簧振子做简谐运动,M点和N点为最大位移处,从某次通
过A点开始计时,经过 2s后振子第一次以与A点相同的速度通过B点,再经过 2s振子紧接着又通过B
点,已知物体在 4s内所走过的总路程为 18cm,则下列说法正确的是 ( )
A. 振子做简谐运动的周期可能是 4s B. 振子做简谐运动的周期可能是 8s
C. 振子做简谐运动的振幅可能是 3cm D. 振子做简谐运动的振幅可能是 6cm
E. 振子做简谐运动的振幅可能是 9cm
2.机械波传播的多解性问题
2. (2024·天津·模拟预测) (多选)如图所示,实线是一列简谐横波在 t= 0时刻的波形图,虚线是这列波在 t
= 0.4s时刻的波形图,则下列说法正确的是 ( )
A. 若该列波沿 x轴负方向传播,则周期可能为 0.3s
B. 若该列波沿 x轴负方向传播,则传播速度可能为 20m/s
C. 25若该列波沿 x轴正方向传播,则其可能与频率为 Hz的简谐波发生稳定的干涉现象
6
D. 若该列波沿 x轴正方向传播,则 x= 4m处的质点在 t= 0.15s时加速度可能最大且沿 y轴正方向
03 针对训练
1. (2024·江西景德镇·二模)如图所示为一列沿 x轴正方向传播的简谐横波,t= 0时刻 0~25m区间的波形
图如图中实线,经过 Δt= 0.3s时该区间波形图如图中虚线,已知虚线上波峰对应的平衡位置的横坐标
为 12.5m,质点A平衡位置的横坐标为 xA= 7.5m,则当波速取最小值时质点A的振动方程以及可能的
波速值,正确的是 ( )
2
A. y= 10sin 2.5πt- π cm;225m/s B. y= 10sin 1.25πt+ π cm;425m/s4 4
C. y= 10sin 2.5πt+ π cm 625m/s D. y= 10sin 1.25πt- π; cm,825m/s4 4
2. (2024·贵州铜仁·二模)如图所示,一列简谐横波沿 x轴传播,振幅为 10cm。实线为 t= 0时刻的波形图,
此时 x= 7cm处的质点P运动方向沿 y轴负方向,虚线为 t= 0.1s的波形图。已知周期T大于 0.1s,则
该波的传播速度和周期分别为 ( )
A. 0.2m/s 0.4s B. 0.4m/s 0.2s C. 2 m/s 0.6s D. 0.6m/s 2, , , , s
15 15
3. (2024·广西玉林·模拟预测)一列沿 x轴正方向传播的简谐横波,振幅为 2cm,波速为 2m/s。如图,在波的
传播方向上两质点 a、b的平衡位置相距 0.4m(小于一个波长),当质点 a在波峰位置时,质点 b在 x轴下
方与 x轴相距 1cm的位置。则下列说法不正确的是 ( )
A. 从此时刻起经过 0.5s,b点可能在波谷位置 B. 从此时刻起经过 0.5s,b点可能在波峰位置
C. 此波的周期可能为 0.6s D. 此波的周期可能为 1.0s
4. (2024·黑龙江·三模)一列简谐横波在 t= 0时的波形如图中实线所示,t= 1s时的波形如图中虚线所示,
则下列说法正确的是 ( )
A. 这列波的波长为 8m
3
B. 平衡位置分别为A、B的两个质点,振动方向始终相同
C. 若波向右传播,则波的最大频率为 0.25Hz
D. 若波向左传播,则波的传播速度大小为 6m/s
5. (2024·山东·模拟预测)一个小球在平衡位置O点附近做简谐运动,t= 0时刻小球位于O点,t1= 2s时小
球首次位于P点,t2= 16s时小球也位于P点,且与 t1时刻速度方向相反。已知P、O两点不重合,则该
小球做简谐运动的周期可能为 ( )
A. 7s B. 12s C. 4s D. 14 s
3
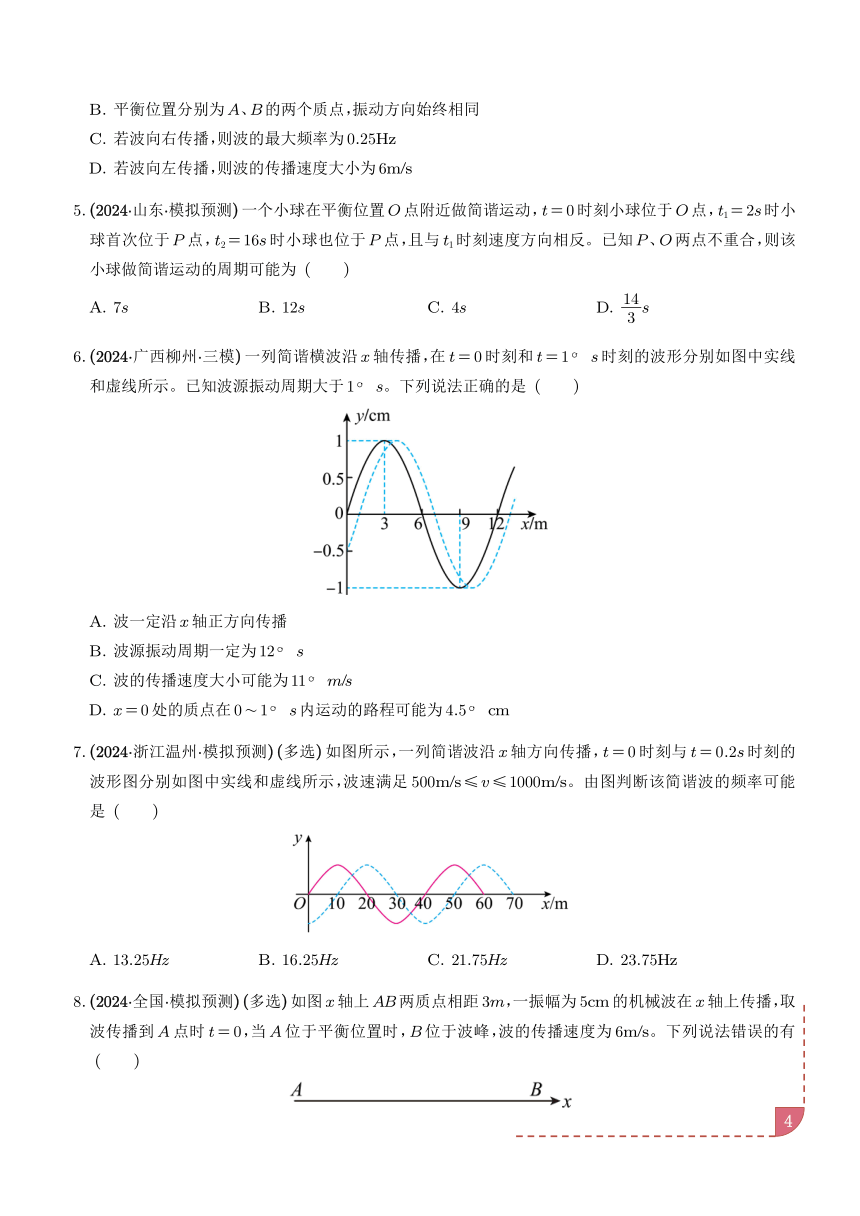
6. (2024·广西柳州·三模)一列简谐横波沿 x轴传播,在 t= 0时刻和 t= 1 s时刻的波形分别如图中实线
和虚线所示。已知波源振动周期大于 1 s。下列说法正确的是 ( )
A. 波一定沿 x轴正方向传播
B. 波源振动周期一定为 12 s
C. 波的传播速度大小可能为 11 m/s
D. x= 0处的质点在 0 1 s内运动的路程可能为 4.5 cm
7. (2024·浙江温州·模拟预测) (多选)如图所示,一列简谐波沿 x轴方向传播,t= 0时刻与 t= 0.2s时刻的
波形图分别如图中实线和虚线所示,波速满足 500m/s≤ v≤ 1000m/s。由图判断该简谐波的频率可能
是 ( )
A. 13.25Hz B. 16.25Hz C. 21.75Hz D. 23.75Hz
8. (2024·全国·模拟预测) (多选)如图 x轴上AB两质点相距 3m,一振幅为 5cm的机械波在 x轴上传播,取
波传播到A点时 t= 0,当A位于平衡位置时,B位于波峰,波的传播速度为 6m/s。下列说法错误的有
( )
4
A. 4被机械波的波长可能为 m
3
B. 机械波的周期最长为 2s
C. 当周期最长时,t= 6s时,B的路程可能为 52cm
D. 当周期最长时,t= 4s时,B的路程可能为 42cm
9. (2025·浙江·一模) (多选)如图所示,S1为振源,某时刻由平衡位置开始上下振动,产生一列简谐横波沿
S1S2直线传播。 S2左侧为介质 I,右侧为介质Ⅱ,波在这两种介质中传播的速度之比为 3:4。某时刻波
正好传到S2右侧 5m处,且S2在波峰位置。下列说法正确的是 ( )
A. S2处质点的起振方向与S1的起振方向相同
B. 波在介质 I中的周期比在介质Ⅱ中小
C. 波在介质 I中的波长可能为 5m
D. 20波在介质Ⅱ中的波长为 + m n=1,2,3, 2n 1
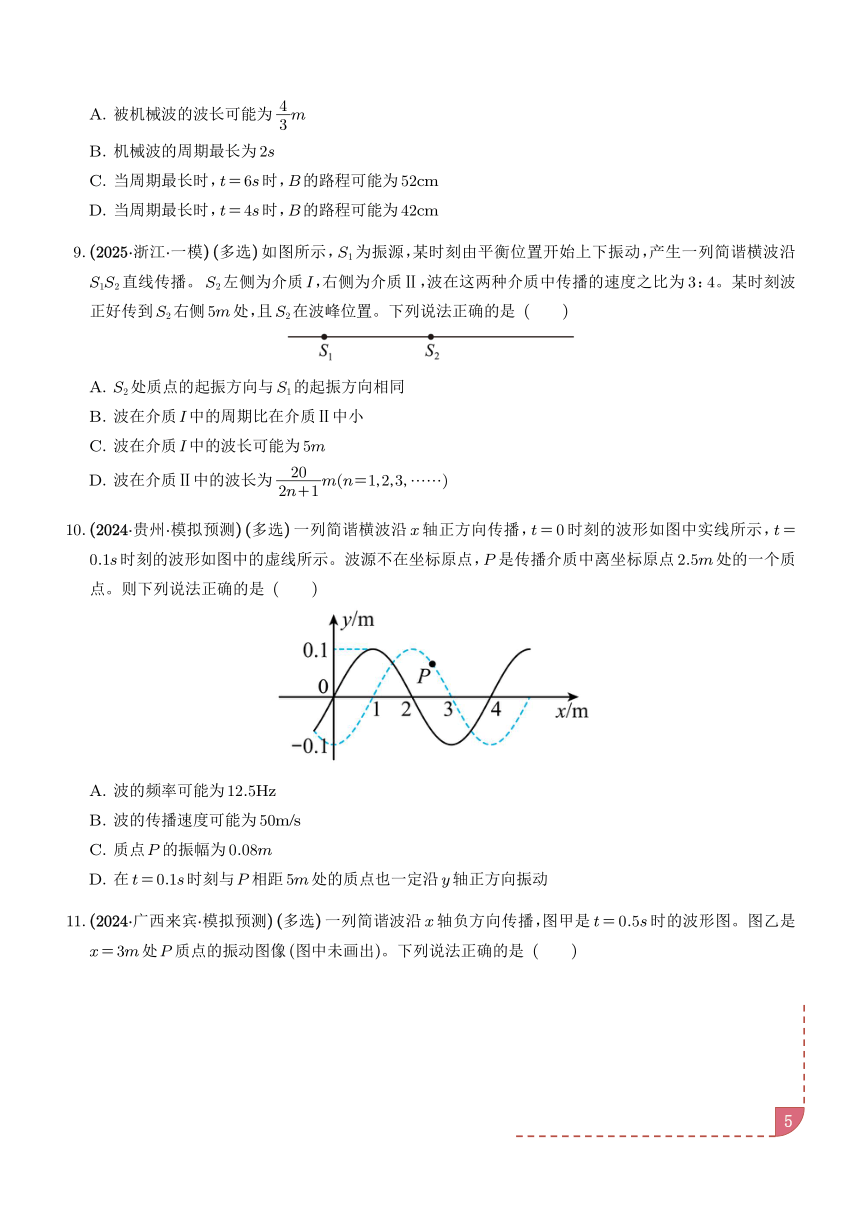
10. (2024·贵州·模拟预测) (多选)一列简谐横波沿 x轴正方向传播,t= 0时刻的波形如图中实线所示,t=
0.1s时刻的波形如图中的虚线所示。波源不在坐标原点,P是传播介质中离坐标原点 2.5m处的一个质
点。则下列说法正确的是 ( )
A. 波的频率可能为 12.5Hz
B. 波的传播速度可能为 50m/s
C. 质点P的振幅为 0.08m
D. 在 t= 0.1s时刻与P相距 5m处的质点也一定沿 y轴正方向振动
11. (2024·广西来宾·模拟预测) (多选)一列简谐波沿 x轴负方向传播,图甲是 t= 0.5s时的波形图。图乙是
x= 3m处P质点的振动图像 (图中未画出)。下列说法正确的是 ( )
5
A. t= 0.5s时,质点P的位移为 yP=-15 2 cm
B. t= 0.5s到 t= 0.9s时间内,P质点的路程为 0.6m
C. 该简谐横波的波长为 8m
D. 该简谐横波的传播速度可能为 10m/s
12. (2024·广东·模拟预测) (多选)如图所示,P、S、Q是弹性介质中、同一直线上的三个点,SQ= 3m,SP=
4m,在 S点有一波源,t= 0时刻,波源开始向上振动,形成沿直线向右、向左传播的两列简谐横波。已
知 t= 7s时,质点 P位于波谷;t= 8s时,质点Q位于波峰。则在 t= 6s时刻 P、Q间的波形图可能是
( )
A. B.
C. D.
13. (2024·黑龙江吉林·模拟预测) (多选)有一列沿水平方向传播的简谐横波,在波的传播方向上有平衡位置
相距 4m的A、B两质点,已知波的传播方向由B指向A,图甲、乙分别是A、B两质点的振动图像。则这
列波的波速可能为 ( )
A. 40m/s B. 12m/s C. 40m/s D. 60m/s
9
14. (2024·河北沧州·三模) (多选)如图所示,沿水平方向做简谐运动的质点,经A点后向右运动,从质点经过
A点时开始计时,t1= 1s时质点经过B点,t2= 3s时质点也经过B点,已知A、B两点相距 0.2m且关于
质点的平衡位置对称,则下列说法正确的是 ( )
6
A. 该振动的振幅和周期可能是 0.1m,1s
B. 该振动的振幅和周期可能是 0.1m,0.4s
C. 若 t1、t2时刻均向左经过B点,则振幅和周期可能为 0.2m,0.4s
D. 若 t 61、t2时刻分别向右、向左经过B点,则振幅和周期可能为 0.2m, s7
7
简谐运动的多解性与机械波传播的多解性问题
学校:_________班级:___________姓名:_____________
01 模型概述
1.简谐运动的周期性与对称性
1)周期性
①相隔Δt= n+ 1 T(n= 0,1,2,3 )的两个时刻,弹簧振子的位置关于平衡位置对称,位移等大反2
向 (或都为零),速度等大反向 (或都为零),加速度等大反向 (或都为零).
②相隔Δt=nT(n= 0,1,2,3 )的两个时刻,弹簧振子在同一位置,位移、速度和加速度都相同.
2)对称性
关于平衡位置O对称的两点,速度的大小、动能、势能、相对平衡位置的位移大小相等,由对称点向平衡
位置O运动时用时相等
2.波传播问题的多解性问题及分析思路
1)造成造成波传播问题多解的主要因素
①周期性
a)时间周期性:时间间隔Δt与周期T的关系不明确.
b)空间周期性:波传播的距离Δx与波长 λ的关系不明确.
②双向性
a)传播方向双向性:波的传播方向不确定.
b)振动方向双向性:质点振动方向不确定.
2)解决波的多解问题的思路
①首先考虑传播方向的双向性:如果题目未说明波的传播方向或没有其他条件暗示,应首先按波传播方
向的可能性进行讨论。
②对设定的传播方向:机械波在一个周期内不同时刻图像的形状是不同的,但在相隔时间为周期整数倍
的不同时刻图像的形状则是相同的,这种周期性必然导致波的传播距离、时间和速度等物理量有多个值与之对
应。
一般采用从特殊到一般的思维方法,先确定最简单的情况,即先找出一个周期 (或一个波长内)内满足
条件的关系Δt或Δx,然后在此基础上加 nT(或nλ)。若此关系为时间,则 t=nT+Δt(n= 0,1,2,3, );若
此关系为距离,则x= nλ+Δx(n= 0,1,2,3, ).最后求速度 v= x = nλ+Δx+ ,其中 n= 0,1,2, 且 kt kT Δt
= 0,1,2, )。
1
02 典题攻破
1.简谐运动的多解性问题
1. (2024·陕西西安·模拟预测) (多选)如图所示,弹簧振子做简谐运动,M点和N点为最大位移处,从某次通
过A点开始计时,经过 2s后振子第一次以与A点相同的速度通过B点,再经过 2s振子紧接着又通过B
点,已知物体在 4s内所走过的总路程为 18cm,则下列说法正确的是 ( )
A. 振子做简谐运动的周期可能是 4s B. 振子做简谐运动的周期可能是 8s
C. 振子做简谐运动的振幅可能是 3cm D. 振子做简谐运动的振幅可能是 6cm
E. 振子做简谐运动的振幅可能是 9cm
【答案】BCE
【详解】AB.若小球通过A点计时是向右运动:由简谐振动的规律可知,因为过A、B两点的速度大小相等,
所以A、B两点一定关于平衡位置O对称,此时通过A、B两点的速度方向相同,所以有从O到B的时间为
1s T,而从B到速度为零的位置为 1s,所以 = 2s
4
解得T= 8s
若小球通过A点计时是向左运动,由简谐振动的规律可知,因为过A、B两点的速度相等,所以A、B两点一
定关于平衡位置O对称,此时经过A、B两点的速度方向相反,设从A到B的时间为 t1,从B到最右端的时间
为 t2,由对称性有
4t2+ t1= 2s
2t2+ 2t1= 2s
其周期为T= 2t1+ 4t2= 8 s3
8
综上所述,振子做简谐运动的周期可能是 8s或者 s,故A错误,B正确;
3
CDE.若小球通过A点计时是向右运动:由简谐振动的规律可知,因为过A、B两点的速度大小相等,方向相
反,所以A、B两点一定关于平衡位置O对称,由对称性有 2A= 18cm
解得A= 9cm
若小球通过A点计时是向左运动,由简谐振动的规律可知,因为过A、B两点的速度相等,所以A、B两点一
定关于平衡位置O对称,此时经过A、B两点的速度方向相反,由对称性有 2A+A+ 2A+A= 18cm
解得A= 3cm
综上所述,振子做简谐运动的振幅可能是 9cm或者 3cm,故CE正确,D错误。
故选BCE。
2.机械波传播的多解性问题
2. (2024·天津·模拟预测) (多选)如图所示,实线是一列简谐横波在 t= 0时刻的波形图,虚线是这列波在 t
= 0.4s时刻的波形图,则下列说法正确的是 ( )
2
A. 若该列波沿 x轴负方向传播,则周期可能为 0.3s
B. 若该列波沿 x轴负方向传播,则传播速度可能为 20m/s
C. 25若该列波沿 x轴正方向传播,则其可能与频率为 Hz的简谐波发生稳定的干涉现象
6
D. 若该列波沿 x轴正方向传播,则 x= 4m处的质点在 t= 0.15s时加速度可能最大且沿 y轴正方向
【答案】AC
【详解】AB.若该波沿 x轴负方向传播,则由实线到虚线需将波形向左平移Δx=nλ+ 4(n= 0,1,2 )
传播的时间Δt= n+ 1 T(n= 0,1,2 )3
T= ΔT可能的周期 (n= 0,1,2 )
n+ 13
Δt 0.4
当n= 1时T= = s= 0.3s
n+ 13 1+
1
3
λ 12
可能的波速 v= = (m/s) = 30n+ 10(m/s)
T 1.2
3n+1
所以波速不可能为 20m/s,A正确,B错误;
C.若该波沿 x轴正方向传播,则由实线到虚线需将波形向右平移Δx=nλ+ 8(n= 0,1,2 )
Δt= n+ 2传播的时间 T(s) (n= 0,1,2 )3
1 1 5 5
波可能的频率 f= = = n+ (Hz)
T Δt 2 3
n+ 23
当n= 1时 f= 5 × 1+ 5 (Hz) = 25 Hz
2 3 6
25
所以可能与频率为 Hz的简谐波发生稳定的干涉现象,C正确;
6
D.由Δt= n+ 2 T(n= 0,1,2 )3
1.2
解得T= + (n= 0,1,2 )x= 4m的质点从 t= 0时刻起经过 t=nT+
3 T(n= 0,1,2 )
3n 2 4
加速度可能最大且沿 y轴正方向,把 t= 0.15s代入上式,可知 n无解,D错误。
故选AC。
03 针对训练
1. (2024·江西景德镇·二模)如图所示为一列沿 x轴正方向传播的简谐横波,t= 0时刻 0~25m区间的波形
图如图中实线,经过 Δt= 0.3s时该区间波形图如图中虚线,已知虚线上波峰对应的平衡位置的横坐标
为 12.5m,质点A平衡位置的横坐标为 xA= 7.5m,则当波速取最小值时质点A的振动方程以及可能的
波速值,正确的是 ( )
3
A. y= 10sin 2.5πt- π cm;225m/s B. y= 10sin 1.25πt+ π cm;425m/s4 4
C. y= 10sin 2.5πt+ π cm;625m/s D. y= 10sin 1.25πt- π cm,825m/s4 4
【答案】C
【详解】由波形图可知,波长为 λ= 20m
x
波沿 x轴正方向传播,则Δt= AT+nT(n= 0,1,2,3,...)
λ
T= 12解得 + s(n= 0,1,2,3,...)40n 15
λ
则波速 v= = 200n+75m/s(n= 0,1,2,3...)n= 0时,波速最小,此时T= 0.8s
T 3
则ω= 2π = 2.5πrad/s
T
质点A的振动方程 y= 10sin 2.5πt+θ cm
π
质点A在零时刻向上振,可知 θ=
4
故质点A的振动方程 y= 10sin 2.5πt+ π cm4
当n= 9时,有 v= 625m/s
故选C。
2. (2024·贵州铜仁·二模)如图所示,一列简谐横波沿 x轴传播,振幅为 10cm。实线为 t= 0时刻的波形图,
此时 x= 7cm处的质点P运动方向沿 y轴负方向,虚线为 t= 0.1s的波形图。已知周期T大于 0.1s,则
该波的传播速度和周期分别为 ( )
A. 0.2m/s,0.4s B. 0.4m/s,0.2s C. 2 m/s 2,0.6s D. 0.6m/s, s
15 15
【答案】D
【详解】由于质点P在 t= 0是向 y轴负方向运动,根据波形图可知,该波的传播方向为沿 x轴正方向。结合题
3
图有 T+nT= 0.1s(n= 0、1、2 )
4
整理有T= 0.4+ s(n= 0、1、2 )4n 3
4
2
由于周期大于 0.1s,所以解得T= s
15
λ
由题图可知,该波的波长为 8cm,则其波速为 v=
T
解得 v= 0.6m/s
故选D。
3. (2024·广西玉林·模拟预测)一列沿 x轴正方向传播的简谐横波,振幅为 2cm,波速为 2m/s。如图,在波的
传播方向上两质点 a、b的平衡位置相距 0.4m(小于一个波长),当质点 a在波峰位置时,质点 b在 x轴下
方与 x轴相距 1cm的位置。则下列说法不正确的是 ( )
A. 从此时刻起经过 0.5s,b点可能在波谷位置 B. 从此时刻起经过 0.5s,b点可能在波峰位置
C. 此波的周期可能为 0.6s D. 此波的周期可能为 1.0s
【答案】D
【详解】AC.第一种情况如图所示
1 + 1根据图像得 λ= 0.4m4 12
解得 λ= 1.2m
周期为T= λ = 0.6s
v
再经 0.5s,波向右移动的距离为Δx= vt= 1m
波形向右移动 1m,波峰在 1m处,如图所示
从图像可知,b点在波谷处。故AC正确,与题意不符;
BD.第二种情况,如图所示
5
1 1
根据图像得 + - 14 2 12 λ= 0.4m
解得 λ= 0.6m
T= λ周期为 = 0.3s
v
再经 0.5s,波向右移动的距离为Δx= vt= 1m= 0.6m+ 0.4m
波形向右移动 0.4m,波峰在 0.4m处,如图所示
根据图像,b点在波峰处。故B正确,与题意不符;D错误,与题意相符。
本题选不正确的故选D。
4. (2024·黑龙江·三模)一列简谐横波在 t= 0时的波形如图中实线所示,t= 1s时的波形如图中虚线所示,
则下列说法正确的是 ( )
A. 这列波的波长为 8m
B. 平衡位置分别为A、B的两个质点,振动方向始终相同
C. 若波向右传播,则波的最大频率为 0.25Hz
D. 若波向左传播,则波的传播速度大小为 6m/s
【答案】A
【详解】A.由图可知,这列波的波长为 λ= 8m,A正确;
B λ.A、B两个质点的平衡位置相距Δx= 4m=
2
故振动方向始终相反,B错误;
C 1.若波向右传播,有 +n T= 1s n=0,1,2 4
T= 4解得 s n=0,1,2
1+4n
6
则波的最小频率为 f= 0.25Hz
C错误;
D 3.若波向左传播,有 +n4 T= 1s n=0,1,2
解得T= 4+ s n=0,1,2 3 4n
λ
则波的传播速度大小为 v= = 6+8n m/s n=0,1,2
T
D错误。
故选A。
5. (2024·山东·模拟预测)一个小球在平衡位置O点附近做简谐运动,t= 0时刻小球位于O点,t1= 2s时小
球首次位于P点,t2= 16s时小球也位于P点,且与 t1时刻速度方向相反。已知P、O两点不重合,则该
小球做简谐运动的周期可能为 ( )
A. 7s B. 12s C. 4s D. 14 s
3
【答案】B
T
【详解】假设P点在O点的左侧,小球向左运动,由 ≥ 2s
4
得T≥ 8s
设经过时间 t小球由P点首次运动到最左端,有
2t+nT= 14s
t+ 2s= T
4
36
解得T= s
2n+1
可知n仅能取 0或 1,当n= 0时T= 36s
当n= 1时T= 12s
或者满足 nT= 14s
可取n= 1,此时T= 14s
T 3
假设P点在O的右侧,小球向左运动,有 < 2s≤ T
2 4
8
解得 s≤T< 4s
3
设经过时间 t小球由P点首次运动到最右端,有
2t+nT= 14s
t+ 2s= 3T
4
T= 36解得
2n+ s3
仅当n= 4时有解,此时T= 36 s
11
或者满足 nT= 14s
可取n= 4或者 5,当n= 4时T= 14 s
4
当n= 5s时T= 14 s
5
故选B。
6. (2024·广西柳州·三模)一列简谐横波沿 x轴传播,在 t= 0时刻和 t= 1 s时刻的波形分别如图中实线
7
和虚线所示。已知波源振动周期大于 1 s。下列说法正确的是 ( )
A. 波一定沿 x轴正方向传播
B. 波源振动周期一定为 12 s
C. 波的传播速度大小可能为 11 m/s
D. x= 0处的质点在 0 1 s内运动的路程可能为 4.5 cm
【答案】C
【详解】AB.由于题中没说明波的传播方向,要分情况讨论:1、假设波沿 x轴负方向传播,设传播周期为T1,
实线波上 x= 0的质点的振动方向向上,其振动方程为 y=Asinωt
结合图有 y= 1sinωt
2π
当 t= 1s时 x= 0处质点位于-0.5cm位置,代入方程有-0.5= 1sin
T1
2π
解得 =- π + 2nπ(n= 0,1,2...)
T1 6
12
化简得T1= - + (n= 0,1,2...)1 12n
其中T1> 1s
n= 1 T = 12则 时解得 1 s11
2、假设波沿 x轴正方向传播,设传播周期为T2,实线波上 x= 0的质点的振动方向向下,其振动方程为 y=
1sin ωt+π
当 t= 1s时 x= 0处质点位于-0.5cm -0.5= 1sin 2π位置,代入方程有 +πT2
同理解得T2= 12s
以上情况都有可能,故AB错误;
C.由波形图可看出,波长为 λ= 12m
由公式 v= λ
T
可见当波沿 x轴负方向传播时,波速为 11m/s。当波沿 x轴正方向传播时,波速为 1m/s。故C正确;
D.因为 x= 0处的质点在一周期内走过的路程为 4cm,而周期T大于 1s,所以,0- 1s内运动的路程一定小
于 4cm,不可能为 4.5cm,故D错误。
故选C。
7. (2024·浙江温州·模拟预测) (多选)如图所示,一列简谐波沿 x轴方向传播,t= 0时刻与 t= 0.2s时刻的
波形图分别如图中实线和虚线所示,波速满足 500m/s≤ v≤ 1000m/s。由图判断该简谐波的频率可能
是 ( )
8
A. 13.25Hz B. 16.25Hz C. 21.75Hz D. 23.75Hz
【答案】BD
【详解】若波沿 x轴正方向传播,在 0.2s时间内,波传播的距离为
10+nλ= vt(n= 0,1,2 )
v= λf
500m/s≤ v≤ 1000m/s
联立解得 f= 16.25Hz或 f= 21.25Hz
若波沿 x轴负方向传播,在 0.2s时间内,波传播的距离为 30+nλ= vt(n= 0,1,2 )
联立解得 f= 13.75Hz或 f= 18.75Hz或 f= 23.75Hz
故选BD。
8. (2024·全国·模拟预测) (多选)如图 x轴上AB两质点相距 3m,一振幅为 5cm的机械波在 x轴上传播,取
波传播到A点时 t= 0,当A位于平衡位置时,B位于波峰,波的传播速度为 6m/s。下列说法错误的有
( )
A. 4被机械波的波长可能为 m
3
B. 机械波的周期最长为 2s
C. 当周期最长时,t= 6s时,B的路程可能为 52cm
D. 当周期最长时,t= 4s时,B的路程可能为 42cm
【答案】CD
【详解】A.由于A位于平衡位置时,B位于波峰,则有 nλ+ λ = 3m或mλ+ 3λ = 3m
4 4
其中n= 0,1,2,3 ,m= 0,1,2,3
4
若波长为 m,可以解得 n= 2
3
故A正确,不符合题意;
B.根据 v= λ 2 2结合上述解得T=
T 4n+ s或T= s1 4m+3
可知,当n= 0时,周期取最大值 2s,故B正确,不符合题意;
C.结合上述,周期最长为 2s时,AB间距为四分之一个波长,即波传播到B需要时间四分之一周期,t= 6s
l
时,由于Δt= t- AB = 6s- 3 s= 5.5s= 2T+ 3T
v 6 4
则B的路程为 x1= 2× 4× 5cm+ 3× 5cm= 55cm
故C错误,符合题意;
D.周期最长为 2s 3 3T时,结合上述,t= 4s时,由于Δt = 4s- s= 3.5s=T+
6 4
则B的路程为 x2= 4× 5cm+ 3× 5cm= 35cm
故D错误,符合题意。 9
故选CD。
9. (2025·浙江·一模) (多选)如图所示,S1为振源,某时刻由平衡位置开始上下振动,产生一列简谐横波沿
S1S2直线传播。 S2左侧为介质 I,右侧为介质Ⅱ,波在这两种介质中传播的速度之比为 3:4。某时刻波
正好传到S2右侧 5m处,且S2在波峰位置。下列说法正确的是 ( )
A. S2处质点的起振方向与S1的起振方向相同
B. 波在介质 I中的周期比在介质Ⅱ中小
C. 波在介质 I中的波长可能为 5m
D. 20波在介质Ⅱ中的波长为 m n=1,2,3,
2n+1
【答案】AC
【详解】A.质点的起振方向一定与振源的起振方向相同,则 S2处质点的起振方向与S1的起振方向相同,故
A正确;
B.波的振动周期由振源决定,波在介质 I中的周期等于介质Ⅱ中的周期,故B错误;
CD 1.若传到S2时,质点S2从平衡位置向上振动,则有 n+ 4 λ= 5m n=0,1,2,3
20
解得 λ= + m n=0,1,2,3 4n 1
3
若传到S2时,质点S2从平衡位置向下振动,则有 n+ λ= 5m n=0,1,2,3 4
20
解得 λ= + m n=0,1,2,3 4n 3
20
整理可得,波在介质Ⅱ中的波长为 λ= + m n=0,1,2,3 2n 1
由公式 λ= vT可知,由于周期相等,则波在介质 I中的波长与波在介质Ⅱ中的波长等于波在这两种介质中传
3
播的速度之比为 3:4,则波在介质 I中的波长为 λ1= λ= 15+ m n=0,1,2,3 4 2n 1
可知,当n= 1时 λ1= 5m
故C正确,D错误。
故选AC。
10. (2024·贵州·模拟预测) (多选)一列简谐横波沿 x轴正方向传播,t= 0时刻的波形如图中实线所示,t=
0.1s时刻的波形如图中的虚线所示。波源不在坐标原点,P是传播介质中离坐标原点 2.5m处的一个质
点。则下列说法正确的是 ( )
A. 波的频率可能为 12.5Hz
B. 波的传播速度可能为 50m/s
10
C. 质点P的振幅为 0.08m
D. 在 t= 0.1s时刻与P相距 5m处的质点也一定沿 y轴正方向振动
【答案】AB
【详解】A T.波沿 x轴正方向传播,则Δt=nT+
4
周期为T= 0.4+ s(n= 0,1,2,3, )4n 1
1
频率为 f= = 20n+5 Hz(n= 0,1,2,3, )
T 2
所以波的频率可能为 12.5Hz(n= 1),故A正确;
B.波长 λ= 4m
λ
波速 v= = 2(20n+ 5)m/s(n= 0,1,2,3, )
T
波的传播速度可能为 50m/s(n= 1),故B正确;
C.振幅A= 0.1m,故C正确;
D 1.从题图中可知 t= 0.1s时,质点P向上振动,与P相距 5m的质点与质点P相距 1 个波长,若该质点在
4
P点左侧,它正在向下振动,若该质点在P点右侧,它正在向上振动,故D错误。
故选AB。
11. (2024·广西来宾·模拟预测) (多选)一列简谐波沿 x轴负方向传播,图甲是 t= 0.5s时的波形图。图乙是
x= 3m处P质点的振动图像 (图中未画出)。下列说法正确的是 ( )
A. t= 0.5s时,质点P的位移为 yP=-15 2 cm
B. t= 0.5s到 t= 0.9s时间内,P质点的路程为 0.6m
C. 该简谐横波的波长为 8m
D. 该简谐横波的传播速度可能为 10m/s
【答案】AB
2π
【详解】A.由图甲和图乙可知,P质点的振幅为A= 0.3m,周期T= 0.8s,角速度ω= = 2.5π s-1P质点
T
的振动方程为 y= 0.3sin2.5πt m ,所以 t= 0.5s时,质点P的位移为 yP=-15 2 cm
故A正确;
B T.做简谐振动的物体在任意 内,质点的路程都是 2A,故B正确;
2
CD.由于波沿 x轴负方向传播,由图乙可知,t= 0.5s时P质点位移为负值并且向下振动,所以P与原点的
距离满足Δx=nλ+ 5 λ(n= 0,1,2...)
8
24
该简谐波的波长为 λ= + m(n= 0、1、2、4 )5 8n
11
λ
则波长不可能是 8m;由 v=
T
30
可知,该简谐波的波速 v= + m/s(n= 0、1、2、3 )5 8n
波速不可能是 10m/s,故CD错误。
故选AB。
12. (2024·广东·模拟预测) (多选)如图所示,P、S、Q是弹性介质中、同一直线上的三个点,SQ= 3m,SP=
4m,在 S点有一波源,t= 0时刻,波源开始向上振动,形成沿直线向右、向左传播的两列简谐横波。已
知 t= 7s时,质点 P位于波谷;t= 8s时,质点Q位于波峰。则在 t= 6s时刻 P、Q间的波形图可能是
( )
A. B.
C. D.
【答案】AD
【详解】B.依题意,S点两侧的波形应对称。故B错误;
A.假设A正确,即 t= 6s时质点P位于波谷,由于 t= 7s时质点P位于波谷,则可知 1s内波传播了 n个周
期,则 2s内波传播 2n个周期,此情况下 t= 8s时质点Q位于波峰,符合题设。故A正确;
C.假设C正确,t= 6s时P位于波谷,此情况下可知 1s内波传播了 n个周期,则 2 s内波传播 2n个周期,8
s时质点Q位于平衡位置,与题设矛盾。故C错误;
D.假设D正确,6s 1时P位于平衡位置向下运动,可知 1 s内波传播了 +n 个周期,则 2s内波传播4
1 +2n 个周期,8 s时质点Q,位于波峰,符合题设。故D正确。2
故选AD。
13. (2024·黑龙江吉林·模拟预测) (多选)有一列沿水平方向传播的简谐横波,在波的传播方向上有平衡位置
相距 4m的A、B两质点,已知波的传播方向由B指向A,图甲、乙分别是A、B两质点的振动图像。则这
列波的波速可能为 ( )
A. 40m/s B. 12m/s C. 40m/s D. 60m/s
9
【答案】AC
12
1
【详解】根据题意可得 +n4 λ= xAB(n= 0,1,2,3 )
16
所以 λ= + m(n= 0,1,2,3 )1 4n
所以 v= λ = 40 m/s(n= 0,1,2,3 )
T 1+4n
当n= 0时,有 v= 40m/s
当n= 1时,有 v= 8m/s
当n= 2时,有 v= 40m/s
9
故选AC。
14. (2024·河北沧州·三模) (多选)如图所示,沿水平方向做简谐运动的质点,经A点后向右运动,从质点经过
A点时开始计时,t1= 1s时质点经过B点,t2= 3s时质点也经过B点,已知A、B两点相距 0.2m且关于
质点的平衡位置对称,则下列说法正确的是 ( )
A. 该振动的振幅和周期可能是 0.1m,1s
B. 该振动的振幅和周期可能是 0.1m,0.4s
C. 若 t1、t2时刻均向左经过B点,则振幅和周期可能为 0.2m,0.4s
D. 若 t1、t
6
2时刻分别向右、向左经过B点,则振幅和周期可能为 0.2m, s7
【答案】BCD
T
【详解】AB.若振幅A1= 0.1m,在 0~1s时间内根据简谱运动的周期性有 1 +nT1= 1s n=0,1,2, 2
在 1~3s时间内根据简谐运动的周期性有 n T1= 2s n =1,2,3,
当T1= 0.4s时
n= 2
n = 5
满足题意,周期为 1s时不同时满足上述两个公式,故A错误,B正确。
CD.若振幅A1= 0.2m且质点 t1时刻向右经过B点、t2时刻向左经过B点,在 0~1s时间内根据简谐运动的
T
周期性有 2 +nT2= 1s n=0,1,2, 6
T
在 1~3s时间内根据简谐运动的周期性有 2 +n T2= 2s n =0,1,2, 3
6
当T2= s时,n= 17
n = 2
T
若振幅A1= 0.2m且 t1、t2时刻均向左经过B点,在 0~1s时间内根据简谐运动的周期性有 3 +nT2 3=
1s n=0,1,2,
在 1~3s时间内根据简谐运动的周期性有 n T3= 2s n =0,1,2,
当T3= 0.4s时
n= 2
n = 5
故CD正确。
故选BCD。
13
高考物理热点模型含答案
简谐运动的多解性与机械波传播的多解性问题
学校:_________班级:___________姓名:_____________
01 模型概述
1.简谐运动的周期性与对称性
1)周期性
①相隔Δt= n+ 1 T(n= 0,1,2,3 )的两个时刻,弹簧振子的位置关于平衡位置对称,位移等大反2
向 (或都为零),速度等大反向 (或都为零),加速度等大反向 (或都为零).
②相隔Δt=nT(n= 0,1,2,3 )的两个时刻,弹簧振子在同一位置,位移、速度和加速度都相同.
2)对称性
关于平衡位置O对称的两点,速度的大小、动能、势能、相对平衡位置的位移大小相等,由对称点向平衡
位置O运动时用时相等
2.波传播问题的多解性问题及分析思路
1)造成造成波传播问题多解的主要因素
①周期性
a)时间周期性:时间间隔Δt与周期T的关系不明确.
b)空间周期性:波传播的距离Δx与波长 λ的关系不明确.
②双向性
a)传播方向双向性:波的传播方向不确定.
b)振动方向双向性:质点振动方向不确定.
2)解决波的多解问题的思路
①首先考虑传播方向的双向性:如果题目未说明波的传播方向或没有其他条件暗示,应首先按波传播方
向的可能性进行讨论。
②对设定的传播方向:机械波在一个周期内不同时刻图像的形状是不同的,但在相隔时间为周期整数倍
的不同时刻图像的形状则是相同的,这种周期性必然导致波的传播距离、时间和速度等物理量有多个值与之对
应。
一般采用从特殊到一般的思维方法,先确定最简单的情况,即先找出一个周期 (或一个波长内)内满足
条件的关系Δt或Δx,然后在此基础上加 nT(或nλ)。若此关系为时间,则 t=nT+Δt(n= 0,1,2,3, );若
此关系为距离,则x= nλ+Δx( = x nλ+Δxn 0,1,2,3, ).最后求速度 v= = ,其中 n= 0,1,2, 且 k
t kT+Δt
= 0,1,2, )。
1
02 典题攻破
1.简谐运动的多解性问题
1. (2024·陕西西安·模拟预测) (多选)如图所示,弹簧振子做简谐运动,M点和N点为最大位移处,从某次通
过A点开始计时,经过 2s后振子第一次以与A点相同的速度通过B点,再经过 2s振子紧接着又通过B
点,已知物体在 4s内所走过的总路程为 18cm,则下列说法正确的是 ( )
A. 振子做简谐运动的周期可能是 4s B. 振子做简谐运动的周期可能是 8s
C. 振子做简谐运动的振幅可能是 3cm D. 振子做简谐运动的振幅可能是 6cm
E. 振子做简谐运动的振幅可能是 9cm
2.机械波传播的多解性问题
2. (2024·天津·模拟预测) (多选)如图所示,实线是一列简谐横波在 t= 0时刻的波形图,虚线是这列波在 t
= 0.4s时刻的波形图,则下列说法正确的是 ( )
A. 若该列波沿 x轴负方向传播,则周期可能为 0.3s
B. 若该列波沿 x轴负方向传播,则传播速度可能为 20m/s
C. 25若该列波沿 x轴正方向传播,则其可能与频率为 Hz的简谐波发生稳定的干涉现象
6
D. 若该列波沿 x轴正方向传播,则 x= 4m处的质点在 t= 0.15s时加速度可能最大且沿 y轴正方向
03 针对训练
1. (2024·江西景德镇·二模)如图所示为一列沿 x轴正方向传播的简谐横波,t= 0时刻 0~25m区间的波形
图如图中实线,经过 Δt= 0.3s时该区间波形图如图中虚线,已知虚线上波峰对应的平衡位置的横坐标
为 12.5m,质点A平衡位置的横坐标为 xA= 7.5m,则当波速取最小值时质点A的振动方程以及可能的
波速值,正确的是 ( )
2
A. y= 10sin 2.5πt- π cm;225m/s B. y= 10sin 1.25πt+ π cm;425m/s4 4
C. y= 10sin 2.5πt+ π cm 625m/s D. y= 10sin 1.25πt- π; cm,825m/s4 4
2. (2024·贵州铜仁·二模)如图所示,一列简谐横波沿 x轴传播,振幅为 10cm。实线为 t= 0时刻的波形图,
此时 x= 7cm处的质点P运动方向沿 y轴负方向,虚线为 t= 0.1s的波形图。已知周期T大于 0.1s,则
该波的传播速度和周期分别为 ( )
A. 0.2m/s 0.4s B. 0.4m/s 0.2s C. 2 m/s 0.6s D. 0.6m/s 2, , , , s
15 15
3. (2024·广西玉林·模拟预测)一列沿 x轴正方向传播的简谐横波,振幅为 2cm,波速为 2m/s。如图,在波的
传播方向上两质点 a、b的平衡位置相距 0.4m(小于一个波长),当质点 a在波峰位置时,质点 b在 x轴下
方与 x轴相距 1cm的位置。则下列说法不正确的是 ( )
A. 从此时刻起经过 0.5s,b点可能在波谷位置 B. 从此时刻起经过 0.5s,b点可能在波峰位置
C. 此波的周期可能为 0.6s D. 此波的周期可能为 1.0s
4. (2024·黑龙江·三模)一列简谐横波在 t= 0时的波形如图中实线所示,t= 1s时的波形如图中虚线所示,
则下列说法正确的是 ( )
A. 这列波的波长为 8m
3
B. 平衡位置分别为A、B的两个质点,振动方向始终相同
C. 若波向右传播,则波的最大频率为 0.25Hz
D. 若波向左传播,则波的传播速度大小为 6m/s
5. (2024·山东·模拟预测)一个小球在平衡位置O点附近做简谐运动,t= 0时刻小球位于O点,t1= 2s时小
球首次位于P点,t2= 16s时小球也位于P点,且与 t1时刻速度方向相反。已知P、O两点不重合,则该
小球做简谐运动的周期可能为 ( )
A. 7s B. 12s C. 4s D. 14 s
3
6. (2024·广西柳州·三模)一列简谐横波沿 x轴传播,在 t= 0时刻和 t= 1 s时刻的波形分别如图中实线
和虚线所示。已知波源振动周期大于 1 s。下列说法正确的是 ( )
A. 波一定沿 x轴正方向传播
B. 波源振动周期一定为 12 s
C. 波的传播速度大小可能为 11 m/s
D. x= 0处的质点在 0 1 s内运动的路程可能为 4.5 cm
7. (2024·浙江温州·模拟预测) (多选)如图所示,一列简谐波沿 x轴方向传播,t= 0时刻与 t= 0.2s时刻的
波形图分别如图中实线和虚线所示,波速满足 500m/s≤ v≤ 1000m/s。由图判断该简谐波的频率可能
是 ( )
A. 13.25Hz B. 16.25Hz C. 21.75Hz D. 23.75Hz
8. (2024·全国·模拟预测) (多选)如图 x轴上AB两质点相距 3m,一振幅为 5cm的机械波在 x轴上传播,取
波传播到A点时 t= 0,当A位于平衡位置时,B位于波峰,波的传播速度为 6m/s。下列说法错误的有
( )
4
A. 4被机械波的波长可能为 m
3
B. 机械波的周期最长为 2s
C. 当周期最长时,t= 6s时,B的路程可能为 52cm
D. 当周期最长时,t= 4s时,B的路程可能为 42cm
9. (2025·浙江·一模) (多选)如图所示,S1为振源,某时刻由平衡位置开始上下振动,产生一列简谐横波沿
S1S2直线传播。 S2左侧为介质 I,右侧为介质Ⅱ,波在这两种介质中传播的速度之比为 3:4。某时刻波
正好传到S2右侧 5m处,且S2在波峰位置。下列说法正确的是 ( )
A. S2处质点的起振方向与S1的起振方向相同
B. 波在介质 I中的周期比在介质Ⅱ中小
C. 波在介质 I中的波长可能为 5m
D. 20波在介质Ⅱ中的波长为 + m n=1,2,3, 2n 1
10. (2024·贵州·模拟预测) (多选)一列简谐横波沿 x轴正方向传播,t= 0时刻的波形如图中实线所示,t=
0.1s时刻的波形如图中的虚线所示。波源不在坐标原点,P是传播介质中离坐标原点 2.5m处的一个质
点。则下列说法正确的是 ( )
A. 波的频率可能为 12.5Hz
B. 波的传播速度可能为 50m/s
C. 质点P的振幅为 0.08m
D. 在 t= 0.1s时刻与P相距 5m处的质点也一定沿 y轴正方向振动
11. (2024·广西来宾·模拟预测) (多选)一列简谐波沿 x轴负方向传播,图甲是 t= 0.5s时的波形图。图乙是
x= 3m处P质点的振动图像 (图中未画出)。下列说法正确的是 ( )
5
A. t= 0.5s时,质点P的位移为 yP=-15 2 cm
B. t= 0.5s到 t= 0.9s时间内,P质点的路程为 0.6m
C. 该简谐横波的波长为 8m
D. 该简谐横波的传播速度可能为 10m/s
12. (2024·广东·模拟预测) (多选)如图所示,P、S、Q是弹性介质中、同一直线上的三个点,SQ= 3m,SP=
4m,在 S点有一波源,t= 0时刻,波源开始向上振动,形成沿直线向右、向左传播的两列简谐横波。已
知 t= 7s时,质点 P位于波谷;t= 8s时,质点Q位于波峰。则在 t= 6s时刻 P、Q间的波形图可能是
( )
A. B.
C. D.
13. (2024·黑龙江吉林·模拟预测) (多选)有一列沿水平方向传播的简谐横波,在波的传播方向上有平衡位置
相距 4m的A、B两质点,已知波的传播方向由B指向A,图甲、乙分别是A、B两质点的振动图像。则这
列波的波速可能为 ( )
A. 40m/s B. 12m/s C. 40m/s D. 60m/s
9
14. (2024·河北沧州·三模) (多选)如图所示,沿水平方向做简谐运动的质点,经A点后向右运动,从质点经过
A点时开始计时,t1= 1s时质点经过B点,t2= 3s时质点也经过B点,已知A、B两点相距 0.2m且关于
质点的平衡位置对称,则下列说法正确的是 ( )
6
A. 该振动的振幅和周期可能是 0.1m,1s
B. 该振动的振幅和周期可能是 0.1m,0.4s
C. 若 t1、t2时刻均向左经过B点,则振幅和周期可能为 0.2m,0.4s
D. 若 t 61、t2时刻分别向右、向左经过B点,则振幅和周期可能为 0.2m, s7
7
简谐运动的多解性与机械波传播的多解性问题
学校:_________班级:___________姓名:_____________
01 模型概述
1.简谐运动的周期性与对称性
1)周期性
①相隔Δt= n+ 1 T(n= 0,1,2,3 )的两个时刻,弹簧振子的位置关于平衡位置对称,位移等大反2
向 (或都为零),速度等大反向 (或都为零),加速度等大反向 (或都为零).
②相隔Δt=nT(n= 0,1,2,3 )的两个时刻,弹簧振子在同一位置,位移、速度和加速度都相同.
2)对称性
关于平衡位置O对称的两点,速度的大小、动能、势能、相对平衡位置的位移大小相等,由对称点向平衡
位置O运动时用时相等
2.波传播问题的多解性问题及分析思路
1)造成造成波传播问题多解的主要因素
①周期性
a)时间周期性:时间间隔Δt与周期T的关系不明确.
b)空间周期性:波传播的距离Δx与波长 λ的关系不明确.
②双向性
a)传播方向双向性:波的传播方向不确定.
b)振动方向双向性:质点振动方向不确定.
2)解决波的多解问题的思路
①首先考虑传播方向的双向性:如果题目未说明波的传播方向或没有其他条件暗示,应首先按波传播方
向的可能性进行讨论。
②对设定的传播方向:机械波在一个周期内不同时刻图像的形状是不同的,但在相隔时间为周期整数倍
的不同时刻图像的形状则是相同的,这种周期性必然导致波的传播距离、时间和速度等物理量有多个值与之对
应。
一般采用从特殊到一般的思维方法,先确定最简单的情况,即先找出一个周期 (或一个波长内)内满足
条件的关系Δt或Δx,然后在此基础上加 nT(或nλ)。若此关系为时间,则 t=nT+Δt(n= 0,1,2,3, );若
此关系为距离,则x= nλ+Δx(n= 0,1,2,3, ).最后求速度 v= x = nλ+Δx+ ,其中 n= 0,1,2, 且 kt kT Δt
= 0,1,2, )。
1
02 典题攻破
1.简谐运动的多解性问题
1. (2024·陕西西安·模拟预测) (多选)如图所示,弹簧振子做简谐运动,M点和N点为最大位移处,从某次通
过A点开始计时,经过 2s后振子第一次以与A点相同的速度通过B点,再经过 2s振子紧接着又通过B
点,已知物体在 4s内所走过的总路程为 18cm,则下列说法正确的是 ( )
A. 振子做简谐运动的周期可能是 4s B. 振子做简谐运动的周期可能是 8s
C. 振子做简谐运动的振幅可能是 3cm D. 振子做简谐运动的振幅可能是 6cm
E. 振子做简谐运动的振幅可能是 9cm
【答案】BCE
【详解】AB.若小球通过A点计时是向右运动:由简谐振动的规律可知,因为过A、B两点的速度大小相等,
所以A、B两点一定关于平衡位置O对称,此时通过A、B两点的速度方向相同,所以有从O到B的时间为
1s T,而从B到速度为零的位置为 1s,所以 = 2s
4
解得T= 8s
若小球通过A点计时是向左运动,由简谐振动的规律可知,因为过A、B两点的速度相等,所以A、B两点一
定关于平衡位置O对称,此时经过A、B两点的速度方向相反,设从A到B的时间为 t1,从B到最右端的时间
为 t2,由对称性有
4t2+ t1= 2s
2t2+ 2t1= 2s
其周期为T= 2t1+ 4t2= 8 s3
8
综上所述,振子做简谐运动的周期可能是 8s或者 s,故A错误,B正确;
3
CDE.若小球通过A点计时是向右运动:由简谐振动的规律可知,因为过A、B两点的速度大小相等,方向相
反,所以A、B两点一定关于平衡位置O对称,由对称性有 2A= 18cm
解得A= 9cm
若小球通过A点计时是向左运动,由简谐振动的规律可知,因为过A、B两点的速度相等,所以A、B两点一
定关于平衡位置O对称,此时经过A、B两点的速度方向相反,由对称性有 2A+A+ 2A+A= 18cm
解得A= 3cm
综上所述,振子做简谐运动的振幅可能是 9cm或者 3cm,故CE正确,D错误。
故选BCE。
2.机械波传播的多解性问题
2. (2024·天津·模拟预测) (多选)如图所示,实线是一列简谐横波在 t= 0时刻的波形图,虚线是这列波在 t
= 0.4s时刻的波形图,则下列说法正确的是 ( )
2
A. 若该列波沿 x轴负方向传播,则周期可能为 0.3s
B. 若该列波沿 x轴负方向传播,则传播速度可能为 20m/s
C. 25若该列波沿 x轴正方向传播,则其可能与频率为 Hz的简谐波发生稳定的干涉现象
6
D. 若该列波沿 x轴正方向传播,则 x= 4m处的质点在 t= 0.15s时加速度可能最大且沿 y轴正方向
【答案】AC
【详解】AB.若该波沿 x轴负方向传播,则由实线到虚线需将波形向左平移Δx=nλ+ 4(n= 0,1,2 )
传播的时间Δt= n+ 1 T(n= 0,1,2 )3
T= ΔT可能的周期 (n= 0,1,2 )
n+ 13
Δt 0.4
当n= 1时T= = s= 0.3s
n+ 13 1+
1
3
λ 12
可能的波速 v= = (m/s) = 30n+ 10(m/s)
T 1.2
3n+1
所以波速不可能为 20m/s,A正确,B错误;
C.若该波沿 x轴正方向传播,则由实线到虚线需将波形向右平移Δx=nλ+ 8(n= 0,1,2 )
Δt= n+ 2传播的时间 T(s) (n= 0,1,2 )3
1 1 5 5
波可能的频率 f= = = n+ (Hz)
T Δt 2 3
n+ 23
当n= 1时 f= 5 × 1+ 5 (Hz) = 25 Hz
2 3 6
25
所以可能与频率为 Hz的简谐波发生稳定的干涉现象,C正确;
6
D.由Δt= n+ 2 T(n= 0,1,2 )3
1.2
解得T= + (n= 0,1,2 )x= 4m的质点从 t= 0时刻起经过 t=nT+
3 T(n= 0,1,2 )
3n 2 4
加速度可能最大且沿 y轴正方向,把 t= 0.15s代入上式,可知 n无解,D错误。
故选AC。
03 针对训练
1. (2024·江西景德镇·二模)如图所示为一列沿 x轴正方向传播的简谐横波,t= 0时刻 0~25m区间的波形
图如图中实线,经过 Δt= 0.3s时该区间波形图如图中虚线,已知虚线上波峰对应的平衡位置的横坐标
为 12.5m,质点A平衡位置的横坐标为 xA= 7.5m,则当波速取最小值时质点A的振动方程以及可能的
波速值,正确的是 ( )
3
A. y= 10sin 2.5πt- π cm;225m/s B. y= 10sin 1.25πt+ π cm;425m/s4 4
C. y= 10sin 2.5πt+ π cm;625m/s D. y= 10sin 1.25πt- π cm,825m/s4 4
【答案】C
【详解】由波形图可知,波长为 λ= 20m
x
波沿 x轴正方向传播,则Δt= AT+nT(n= 0,1,2,3,...)
λ
T= 12解得 + s(n= 0,1,2,3,...)40n 15
λ
则波速 v= = 200n+75m/s(n= 0,1,2,3...)n= 0时,波速最小,此时T= 0.8s
T 3
则ω= 2π = 2.5πrad/s
T
质点A的振动方程 y= 10sin 2.5πt+θ cm
π
质点A在零时刻向上振,可知 θ=
4
故质点A的振动方程 y= 10sin 2.5πt+ π cm4
当n= 9时,有 v= 625m/s
故选C。
2. (2024·贵州铜仁·二模)如图所示,一列简谐横波沿 x轴传播,振幅为 10cm。实线为 t= 0时刻的波形图,
此时 x= 7cm处的质点P运动方向沿 y轴负方向,虚线为 t= 0.1s的波形图。已知周期T大于 0.1s,则
该波的传播速度和周期分别为 ( )
A. 0.2m/s,0.4s B. 0.4m/s,0.2s C. 2 m/s 2,0.6s D. 0.6m/s, s
15 15
【答案】D
【详解】由于质点P在 t= 0是向 y轴负方向运动,根据波形图可知,该波的传播方向为沿 x轴正方向。结合题
3
图有 T+nT= 0.1s(n= 0、1、2 )
4
整理有T= 0.4+ s(n= 0、1、2 )4n 3
4
2
由于周期大于 0.1s,所以解得T= s
15
λ
由题图可知,该波的波长为 8cm,则其波速为 v=
T
解得 v= 0.6m/s
故选D。
3. (2024·广西玉林·模拟预测)一列沿 x轴正方向传播的简谐横波,振幅为 2cm,波速为 2m/s。如图,在波的
传播方向上两质点 a、b的平衡位置相距 0.4m(小于一个波长),当质点 a在波峰位置时,质点 b在 x轴下
方与 x轴相距 1cm的位置。则下列说法不正确的是 ( )
A. 从此时刻起经过 0.5s,b点可能在波谷位置 B. 从此时刻起经过 0.5s,b点可能在波峰位置
C. 此波的周期可能为 0.6s D. 此波的周期可能为 1.0s
【答案】D
【详解】AC.第一种情况如图所示
1 + 1根据图像得 λ= 0.4m4 12
解得 λ= 1.2m
周期为T= λ = 0.6s
v
再经 0.5s,波向右移动的距离为Δx= vt= 1m
波形向右移动 1m,波峰在 1m处,如图所示
从图像可知,b点在波谷处。故AC正确,与题意不符;
BD.第二种情况,如图所示
5
1 1
根据图像得 + - 14 2 12 λ= 0.4m
解得 λ= 0.6m
T= λ周期为 = 0.3s
v
再经 0.5s,波向右移动的距离为Δx= vt= 1m= 0.6m+ 0.4m
波形向右移动 0.4m,波峰在 0.4m处,如图所示
根据图像,b点在波峰处。故B正确,与题意不符;D错误,与题意相符。
本题选不正确的故选D。
4. (2024·黑龙江·三模)一列简谐横波在 t= 0时的波形如图中实线所示,t= 1s时的波形如图中虚线所示,
则下列说法正确的是 ( )
A. 这列波的波长为 8m
B. 平衡位置分别为A、B的两个质点,振动方向始终相同
C. 若波向右传播,则波的最大频率为 0.25Hz
D. 若波向左传播,则波的传播速度大小为 6m/s
【答案】A
【详解】A.由图可知,这列波的波长为 λ= 8m,A正确;
B λ.A、B两个质点的平衡位置相距Δx= 4m=
2
故振动方向始终相反,B错误;
C 1.若波向右传播,有 +n T= 1s n=0,1,2 4
T= 4解得 s n=0,1,2
1+4n
6
则波的最小频率为 f= 0.25Hz
C错误;
D 3.若波向左传播,有 +n4 T= 1s n=0,1,2
解得T= 4+ s n=0,1,2 3 4n
λ
则波的传播速度大小为 v= = 6+8n m/s n=0,1,2
T
D错误。
故选A。
5. (2024·山东·模拟预测)一个小球在平衡位置O点附近做简谐运动,t= 0时刻小球位于O点,t1= 2s时小
球首次位于P点,t2= 16s时小球也位于P点,且与 t1时刻速度方向相反。已知P、O两点不重合,则该
小球做简谐运动的周期可能为 ( )
A. 7s B. 12s C. 4s D. 14 s
3
【答案】B
T
【详解】假设P点在O点的左侧,小球向左运动,由 ≥ 2s
4
得T≥ 8s
设经过时间 t小球由P点首次运动到最左端,有
2t+nT= 14s
t+ 2s= T
4
36
解得T= s
2n+1
可知n仅能取 0或 1,当n= 0时T= 36s
当n= 1时T= 12s
或者满足 nT= 14s
可取n= 1,此时T= 14s
T 3
假设P点在O的右侧,小球向左运动,有 < 2s≤ T
2 4
8
解得 s≤T< 4s
3
设经过时间 t小球由P点首次运动到最右端,有
2t+nT= 14s
t+ 2s= 3T
4
T= 36解得
2n+ s3
仅当n= 4时有解,此时T= 36 s
11
或者满足 nT= 14s
可取n= 4或者 5,当n= 4时T= 14 s
4
当n= 5s时T= 14 s
5
故选B。
6. (2024·广西柳州·三模)一列简谐横波沿 x轴传播,在 t= 0时刻和 t= 1 s时刻的波形分别如图中实线
7
和虚线所示。已知波源振动周期大于 1 s。下列说法正确的是 ( )
A. 波一定沿 x轴正方向传播
B. 波源振动周期一定为 12 s
C. 波的传播速度大小可能为 11 m/s
D. x= 0处的质点在 0 1 s内运动的路程可能为 4.5 cm
【答案】C
【详解】AB.由于题中没说明波的传播方向,要分情况讨论:1、假设波沿 x轴负方向传播,设传播周期为T1,
实线波上 x= 0的质点的振动方向向上,其振动方程为 y=Asinωt
结合图有 y= 1sinωt
2π
当 t= 1s时 x= 0处质点位于-0.5cm位置,代入方程有-0.5= 1sin
T1
2π
解得 =- π + 2nπ(n= 0,1,2...)
T1 6
12
化简得T1= - + (n= 0,1,2...)1 12n
其中T1> 1s
n= 1 T = 12则 时解得 1 s11
2、假设波沿 x轴正方向传播,设传播周期为T2,实线波上 x= 0的质点的振动方向向下,其振动方程为 y=
1sin ωt+π
当 t= 1s时 x= 0处质点位于-0.5cm -0.5= 1sin 2π位置,代入方程有 +πT2
同理解得T2= 12s
以上情况都有可能,故AB错误;
C.由波形图可看出,波长为 λ= 12m
由公式 v= λ
T
可见当波沿 x轴负方向传播时,波速为 11m/s。当波沿 x轴正方向传播时,波速为 1m/s。故C正确;
D.因为 x= 0处的质点在一周期内走过的路程为 4cm,而周期T大于 1s,所以,0- 1s内运动的路程一定小
于 4cm,不可能为 4.5cm,故D错误。
故选C。
7. (2024·浙江温州·模拟预测) (多选)如图所示,一列简谐波沿 x轴方向传播,t= 0时刻与 t= 0.2s时刻的
波形图分别如图中实线和虚线所示,波速满足 500m/s≤ v≤ 1000m/s。由图判断该简谐波的频率可能
是 ( )
8
A. 13.25Hz B. 16.25Hz C. 21.75Hz D. 23.75Hz
【答案】BD
【详解】若波沿 x轴正方向传播,在 0.2s时间内,波传播的距离为
10+nλ= vt(n= 0,1,2 )
v= λf
500m/s≤ v≤ 1000m/s
联立解得 f= 16.25Hz或 f= 21.25Hz
若波沿 x轴负方向传播,在 0.2s时间内,波传播的距离为 30+nλ= vt(n= 0,1,2 )
联立解得 f= 13.75Hz或 f= 18.75Hz或 f= 23.75Hz
故选BD。
8. (2024·全国·模拟预测) (多选)如图 x轴上AB两质点相距 3m,一振幅为 5cm的机械波在 x轴上传播,取
波传播到A点时 t= 0,当A位于平衡位置时,B位于波峰,波的传播速度为 6m/s。下列说法错误的有
( )
A. 4被机械波的波长可能为 m
3
B. 机械波的周期最长为 2s
C. 当周期最长时,t= 6s时,B的路程可能为 52cm
D. 当周期最长时,t= 4s时,B的路程可能为 42cm
【答案】CD
【详解】A.由于A位于平衡位置时,B位于波峰,则有 nλ+ λ = 3m或mλ+ 3λ = 3m
4 4
其中n= 0,1,2,3 ,m= 0,1,2,3
4
若波长为 m,可以解得 n= 2
3
故A正确,不符合题意;
B.根据 v= λ 2 2结合上述解得T=
T 4n+ s或T= s1 4m+3
可知,当n= 0时,周期取最大值 2s,故B正确,不符合题意;
C.结合上述,周期最长为 2s时,AB间距为四分之一个波长,即波传播到B需要时间四分之一周期,t= 6s
l
时,由于Δt= t- AB = 6s- 3 s= 5.5s= 2T+ 3T
v 6 4
则B的路程为 x1= 2× 4× 5cm+ 3× 5cm= 55cm
故C错误,符合题意;
D.周期最长为 2s 3 3T时,结合上述,t= 4s时,由于Δt = 4s- s= 3.5s=T+
6 4
则B的路程为 x2= 4× 5cm+ 3× 5cm= 35cm
故D错误,符合题意。 9
故选CD。
9. (2025·浙江·一模) (多选)如图所示,S1为振源,某时刻由平衡位置开始上下振动,产生一列简谐横波沿
S1S2直线传播。 S2左侧为介质 I,右侧为介质Ⅱ,波在这两种介质中传播的速度之比为 3:4。某时刻波
正好传到S2右侧 5m处,且S2在波峰位置。下列说法正确的是 ( )
A. S2处质点的起振方向与S1的起振方向相同
B. 波在介质 I中的周期比在介质Ⅱ中小
C. 波在介质 I中的波长可能为 5m
D. 20波在介质Ⅱ中的波长为 m n=1,2,3,
2n+1
【答案】AC
【详解】A.质点的起振方向一定与振源的起振方向相同,则 S2处质点的起振方向与S1的起振方向相同,故
A正确;
B.波的振动周期由振源决定,波在介质 I中的周期等于介质Ⅱ中的周期,故B错误;
CD 1.若传到S2时,质点S2从平衡位置向上振动,则有 n+ 4 λ= 5m n=0,1,2,3
20
解得 λ= + m n=0,1,2,3 4n 1
3
若传到S2时,质点S2从平衡位置向下振动,则有 n+ λ= 5m n=0,1,2,3 4
20
解得 λ= + m n=0,1,2,3 4n 3
20
整理可得,波在介质Ⅱ中的波长为 λ= + m n=0,1,2,3 2n 1
由公式 λ= vT可知,由于周期相等,则波在介质 I中的波长与波在介质Ⅱ中的波长等于波在这两种介质中传
3
播的速度之比为 3:4,则波在介质 I中的波长为 λ1= λ= 15+ m n=0,1,2,3 4 2n 1
可知,当n= 1时 λ1= 5m
故C正确,D错误。
故选AC。
10. (2024·贵州·模拟预测) (多选)一列简谐横波沿 x轴正方向传播,t= 0时刻的波形如图中实线所示,t=
0.1s时刻的波形如图中的虚线所示。波源不在坐标原点,P是传播介质中离坐标原点 2.5m处的一个质
点。则下列说法正确的是 ( )
A. 波的频率可能为 12.5Hz
B. 波的传播速度可能为 50m/s
10
C. 质点P的振幅为 0.08m
D. 在 t= 0.1s时刻与P相距 5m处的质点也一定沿 y轴正方向振动
【答案】AB
【详解】A T.波沿 x轴正方向传播,则Δt=nT+
4
周期为T= 0.4+ s(n= 0,1,2,3, )4n 1
1
频率为 f= = 20n+5 Hz(n= 0,1,2,3, )
T 2
所以波的频率可能为 12.5Hz(n= 1),故A正确;
B.波长 λ= 4m
λ
波速 v= = 2(20n+ 5)m/s(n= 0,1,2,3, )
T
波的传播速度可能为 50m/s(n= 1),故B正确;
C.振幅A= 0.1m,故C正确;
D 1.从题图中可知 t= 0.1s时,质点P向上振动,与P相距 5m的质点与质点P相距 1 个波长,若该质点在
4
P点左侧,它正在向下振动,若该质点在P点右侧,它正在向上振动,故D错误。
故选AB。
11. (2024·广西来宾·模拟预测) (多选)一列简谐波沿 x轴负方向传播,图甲是 t= 0.5s时的波形图。图乙是
x= 3m处P质点的振动图像 (图中未画出)。下列说法正确的是 ( )
A. t= 0.5s时,质点P的位移为 yP=-15 2 cm
B. t= 0.5s到 t= 0.9s时间内,P质点的路程为 0.6m
C. 该简谐横波的波长为 8m
D. 该简谐横波的传播速度可能为 10m/s
【答案】AB
2π
【详解】A.由图甲和图乙可知,P质点的振幅为A= 0.3m,周期T= 0.8s,角速度ω= = 2.5π s-1P质点
T
的振动方程为 y= 0.3sin2.5πt m ,所以 t= 0.5s时,质点P的位移为 yP=-15 2 cm
故A正确;
B T.做简谐振动的物体在任意 内,质点的路程都是 2A,故B正确;
2
CD.由于波沿 x轴负方向传播,由图乙可知,t= 0.5s时P质点位移为负值并且向下振动,所以P与原点的
距离满足Δx=nλ+ 5 λ(n= 0,1,2...)
8
24
该简谐波的波长为 λ= + m(n= 0、1、2、4 )5 8n
11
λ
则波长不可能是 8m;由 v=
T
30
可知,该简谐波的波速 v= + m/s(n= 0、1、2、3 )5 8n
波速不可能是 10m/s,故CD错误。
故选AB。
12. (2024·广东·模拟预测) (多选)如图所示,P、S、Q是弹性介质中、同一直线上的三个点,SQ= 3m,SP=
4m,在 S点有一波源,t= 0时刻,波源开始向上振动,形成沿直线向右、向左传播的两列简谐横波。已
知 t= 7s时,质点 P位于波谷;t= 8s时,质点Q位于波峰。则在 t= 6s时刻 P、Q间的波形图可能是
( )
A. B.
C. D.
【答案】AD
【详解】B.依题意,S点两侧的波形应对称。故B错误;
A.假设A正确,即 t= 6s时质点P位于波谷,由于 t= 7s时质点P位于波谷,则可知 1s内波传播了 n个周
期,则 2s内波传播 2n个周期,此情况下 t= 8s时质点Q位于波峰,符合题设。故A正确;
C.假设C正确,t= 6s时P位于波谷,此情况下可知 1s内波传播了 n个周期,则 2 s内波传播 2n个周期,8
s时质点Q位于平衡位置,与题设矛盾。故C错误;
D.假设D正确,6s 1时P位于平衡位置向下运动,可知 1 s内波传播了 +n 个周期,则 2s内波传播4
1 +2n 个周期,8 s时质点Q,位于波峰,符合题设。故D正确。2
故选AD。
13. (2024·黑龙江吉林·模拟预测) (多选)有一列沿水平方向传播的简谐横波,在波的传播方向上有平衡位置
相距 4m的A、B两质点,已知波的传播方向由B指向A,图甲、乙分别是A、B两质点的振动图像。则这
列波的波速可能为 ( )
A. 40m/s B. 12m/s C. 40m/s D. 60m/s
9
【答案】AC
12
1
【详解】根据题意可得 +n4 λ= xAB(n= 0,1,2,3 )
16
所以 λ= + m(n= 0,1,2,3 )1 4n
所以 v= λ = 40 m/s(n= 0,1,2,3 )
T 1+4n
当n= 0时,有 v= 40m/s
当n= 1时,有 v= 8m/s
当n= 2时,有 v= 40m/s
9
故选AC。
14. (2024·河北沧州·三模) (多选)如图所示,沿水平方向做简谐运动的质点,经A点后向右运动,从质点经过
A点时开始计时,t1= 1s时质点经过B点,t2= 3s时质点也经过B点,已知A、B两点相距 0.2m且关于
质点的平衡位置对称,则下列说法正确的是 ( )
A. 该振动的振幅和周期可能是 0.1m,1s
B. 该振动的振幅和周期可能是 0.1m,0.4s
C. 若 t1、t2时刻均向左经过B点,则振幅和周期可能为 0.2m,0.4s
D. 若 t1、t
6
2时刻分别向右、向左经过B点,则振幅和周期可能为 0.2m, s7
【答案】BCD
T
【详解】AB.若振幅A1= 0.1m,在 0~1s时间内根据简谱运动的周期性有 1 +nT1= 1s n=0,1,2, 2
在 1~3s时间内根据简谐运动的周期性有 n T1= 2s n =1,2,3,
当T1= 0.4s时
n= 2
n = 5
满足题意,周期为 1s时不同时满足上述两个公式,故A错误,B正确。
CD.若振幅A1= 0.2m且质点 t1时刻向右经过B点、t2时刻向左经过B点,在 0~1s时间内根据简谐运动的
T
周期性有 2 +nT2= 1s n=0,1,2, 6
T
在 1~3s时间内根据简谐运动的周期性有 2 +n T2= 2s n =0,1,2, 3
6
当T2= s时,n= 17
n = 2
T
若振幅A1= 0.2m且 t1、t2时刻均向左经过B点,在 0~1s时间内根据简谐运动的周期性有 3 +nT2 3=
1s n=0,1,2,
在 1~3s时间内根据简谐运动的周期性有 n T3= 2s n =0,1,2,
当T3= 0.4s时
n= 2
n = 5
故CD正确。
故选BCD。
13
同课章节目录
