3.1.1 函数的概念(第2课时) 课件(共34张PPT) -高一数学考试满分全攻略同步备课备考系列(人教A版2019必修一)
文档属性
| 名称 | 3.1.1 函数的概念(第2课时) 课件(共34张PPT) -高一数学考试满分全攻略同步备课备考系列(人教A版2019必修一) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 10:12:18 | ||
图片预览











文档简介
(共34张PPT)
人教A版2019高一数学(必修一)第三章 函数的概念与性质
3.1.1 函数的概念(第2课时)
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
1.进一步体会函数是描述变量之间的依赖关系的重要数学模型.能用集合与对应的语言刻画出函数,体会对应关系在刻画数学概念中的作用.(重点、难点)
2.了解构成函数的要素,会求一些简单函数的定义域和值域.(重点)
3.能够正确使用区间表示数集.(易混点)
学习目标
1.函数的概念
一般地,设A,B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作:y=f(x),x∈A.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
2.函数的三要素:定义域、对应法则、值域.
复习导入
1.区间的概念与表示方法
研究函数的时候经常会遇到区间的概念,设是两个实数且,我们规定:
③和④都可以称作半开半闭区间
①满足不等式的实数的集合叫做闭区间,表示为[]
②满足不等式的实数的集合叫做开区间,表示为()
③满足不等式的实数的集合叫做左开右闭区间,表示为(]
④满足不等式的实数的集合叫做左闭右开区间,表示为[)
这里的实数a与b都叫做相应区间的端点
新知探究
闭区间
开区间
左开右闭区间
左闭右开区间
[]
()
(]
[
这些区间的几何表示如表所示.在数轴表示时,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点.
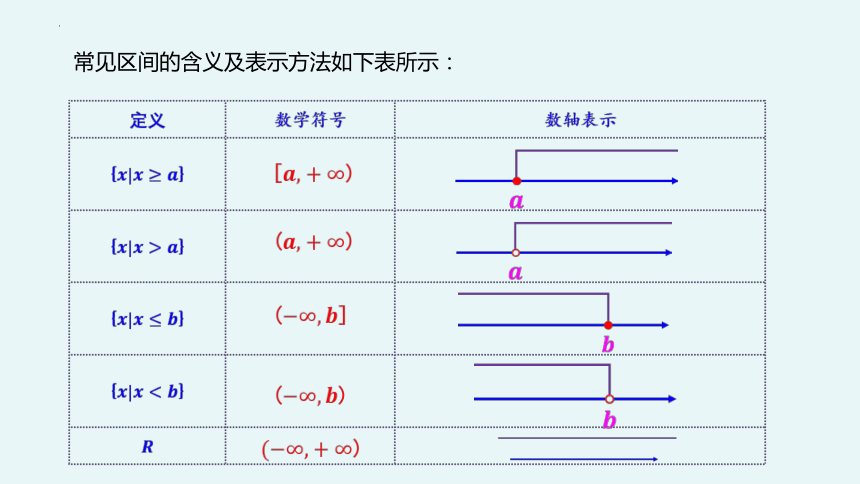
常见区间的含义及表示方法如下表所示:
[)
()
(]
()
)
解:
课本例题
解:
课本例题
解:
课本例题
由函数的定义可知,构成函数的要素为:定义域,对应关系和值域.因为值域是由定义域和对应关系决定的,所以如果两个函数的定义域相同,并且对应关系完全一致,那么这两个函数是同一个函数.
如果两个函数仅仅是对应关系相同,但定义域不同,那么它们肯定不是同一个函数.
如S=350t,t∈{t|0≤t≤0.5}与W=350d,d∈{1,2,3,4,5,6}的对应关系都为y=350x,但它们的定义域不同,所以它们不是同一个函数,同时,因为它们的定义域都不为R,所以它们与正比例函数y=350x,(x∈R)也不是同一个函数.
新知探究
由函数的定义可知,构成函数的要素为:定义域,对应关系和值域.因为值域是由定义域和对应关系决定的,所以如果两个函数的定义域相同,并且对应关系完全一致,那么这两个函数是同一个函数.
新知探究
解:
课本例题
解:
课本例题
课本练习
课本练习
课本练习
易错防范:忽视分母不为零;误以为(x+1)0=1对任意实数成立.防范措施是求函数的定义域时应注意以下几点:①分式的分母不为零;②偶次根式被开方式非负;③零的非正数次幂没有意义;④函数的定义域是非空的数集.
错因分析
典例剖析
总结归纳
关于函数的定义域
(1)依据:分式分母不为0,二次根式的被开方数不小于0,0次幂的底数不为0等.
(2)写法:如果解析式中含有多个式子,则用大括号将x满足的条件列成不等式组,求交集.
总结归纳
总结归纳
总结归纳
总结归纳
核心知识
方法总结
易错提醒
核心素养
抽象函数
同一个函数
常见函数的
定义域与值域
定义域相同
对应关系相同
同一个函数的判断方法:
一看定义域是否相同;
二看对应关系是否相同
函数值域的求法:
(1)观察法:适于简单函数的值域;
(2)配方法::适于“二次函数”类值域;
(3)换元法:运用新元代换,将所给函数化成值域易确定的函数;
(4)分离常数法:将有理分式,转化为“反比例函数类”的形式。
(1)判断同一个函数时函数式化简须是等价变形自变量与用哪个字母表示无关,
(2)抽象函数f(g(x))的定义域由f(x)与g(x)共同决定
函数概念的
综合应用
数学运算:通过函数值域的求法,培养数学运算的核心素养
数学抽象:通过同一个函数的判断,培养数学抽象的核心素养
课堂小结
人教A版2019高一数学(必修一)第三章 函数的概念与性质
3.1.1 函数的概念(第2课时)
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
1.进一步体会函数是描述变量之间的依赖关系的重要数学模型.能用集合与对应的语言刻画出函数,体会对应关系在刻画数学概念中的作用.(重点、难点)
2.了解构成函数的要素,会求一些简单函数的定义域和值域.(重点)
3.能够正确使用区间表示数集.(易混点)
学习目标
1.函数的概念
一般地,设A,B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作:y=f(x),x∈A.
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.
2.函数的三要素:定义域、对应法则、值域.
复习导入
1.区间的概念与表示方法
研究函数的时候经常会遇到区间的概念,设是两个实数且,我们规定:
③和④都可以称作半开半闭区间
①满足不等式的实数的集合叫做闭区间,表示为[]
②满足不等式的实数的集合叫做开区间,表示为()
③满足不等式的实数的集合叫做左开右闭区间,表示为(]
④满足不等式的实数的集合叫做左闭右开区间,表示为[)
这里的实数a与b都叫做相应区间的端点
新知探究
闭区间
开区间
左开右闭区间
左闭右开区间
[]
()
(]
[
这些区间的几何表示如表所示.在数轴表示时,用实心点表示包括在区间内的端点,用空心点表示不包括在区间内的端点.
常见区间的含义及表示方法如下表所示:
[)
()
(]
()
)
解:
课本例题
解:
课本例题
解:
课本例题
由函数的定义可知,构成函数的要素为:定义域,对应关系和值域.因为值域是由定义域和对应关系决定的,所以如果两个函数的定义域相同,并且对应关系完全一致,那么这两个函数是同一个函数.
如果两个函数仅仅是对应关系相同,但定义域不同,那么它们肯定不是同一个函数.
如S=350t,t∈{t|0≤t≤0.5}与W=350d,d∈{1,2,3,4,5,6}的对应关系都为y=350x,但它们的定义域不同,所以它们不是同一个函数,同时,因为它们的定义域都不为R,所以它们与正比例函数y=350x,(x∈R)也不是同一个函数.
新知探究
由函数的定义可知,构成函数的要素为:定义域,对应关系和值域.因为值域是由定义域和对应关系决定的,所以如果两个函数的定义域相同,并且对应关系完全一致,那么这两个函数是同一个函数.
新知探究
解:
课本例题
解:
课本例题
课本练习
课本练习
课本练习
易错防范:忽视分母不为零;误以为(x+1)0=1对任意实数成立.防范措施是求函数的定义域时应注意以下几点:①分式的分母不为零;②偶次根式被开方式非负;③零的非正数次幂没有意义;④函数的定义域是非空的数集.
错因分析
典例剖析
总结归纳
关于函数的定义域
(1)依据:分式分母不为0,二次根式的被开方数不小于0,0次幂的底数不为0等.
(2)写法:如果解析式中含有多个式子,则用大括号将x满足的条件列成不等式组,求交集.
总结归纳
总结归纳
总结归纳
总结归纳
核心知识
方法总结
易错提醒
核心素养
抽象函数
同一个函数
常见函数的
定义域与值域
定义域相同
对应关系相同
同一个函数的判断方法:
一看定义域是否相同;
二看对应关系是否相同
函数值域的求法:
(1)观察法:适于简单函数的值域;
(2)配方法::适于“二次函数”类值域;
(3)换元法:运用新元代换,将所给函数化成值域易确定的函数;
(4)分离常数法:将有理分式,转化为“反比例函数类”的形式。
(1)判断同一个函数时函数式化简须是等价变形自变量与用哪个字母表示无关,
(2)抽象函数f(g(x))的定义域由f(x)与g(x)共同决定
函数概念的
综合应用
数学运算:通过函数值域的求法,培养数学运算的核心素养
数学抽象:通过同一个函数的判断,培养数学抽象的核心素养
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
