3.1.2 函数的表示法(第1课时) 课件(共39张PPT) -高一数学考试满分全攻略同步备课备考系列(人教A版2019必修一)
文档属性
| 名称 | 3.1.2 函数的表示法(第1课时) 课件(共39张PPT) -高一数学考试满分全攻略同步备课备考系列(人教A版2019必修一) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览









文档简介
(共39张PPT)
人教A版2019高一数学(必修一)第三章 函数的概念与性质
3.1.2函数的表示法(第1课时)
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
1.掌握函数的三种表示方法:解析法、图象法、列表法.(重点)
2.会根据不同的需要选择恰当的方法表示函数.(难点)
学习目标
Q1:由我们初中已经接触过了函数常见的三种表示方法,你还记得是哪三种方法吗?请结合教材P60--61的问题1,2,3,4来说明?
(1)解析法:用数学表达式表示两个变量之间的对应关系.
例如:问题1中的S=350t, t∈{t|0≤t≤0.5}
问题2中的w=350d, d∈{1,2,3,4,5}
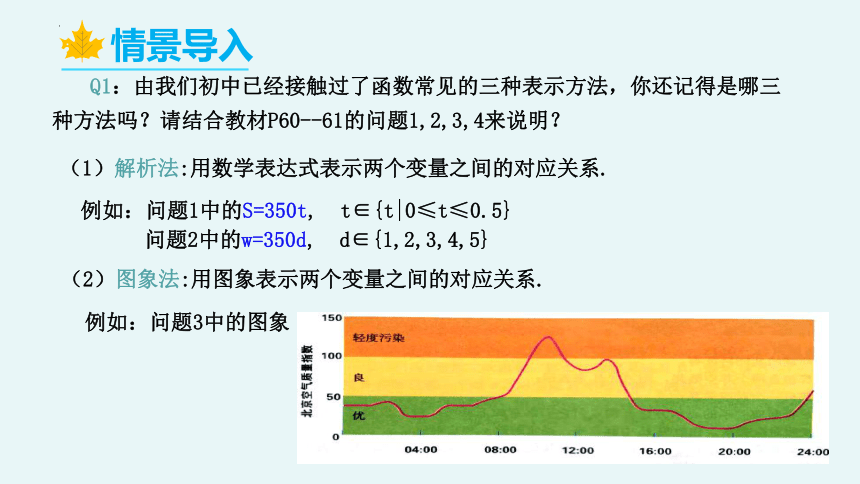
(2)图象法:用图象表示两个变量之间的对应关系.
例如:问题3中的图象
情景导入
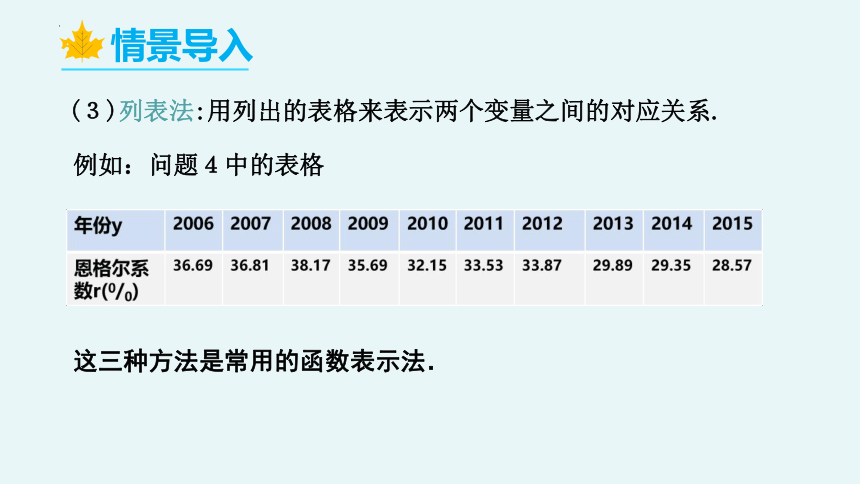
(3)列表法:用列出的表格来表示两个变量之间的对应关系.
例如:问题4中的表格
这三种方法是常用的函数表示法.
情景导入
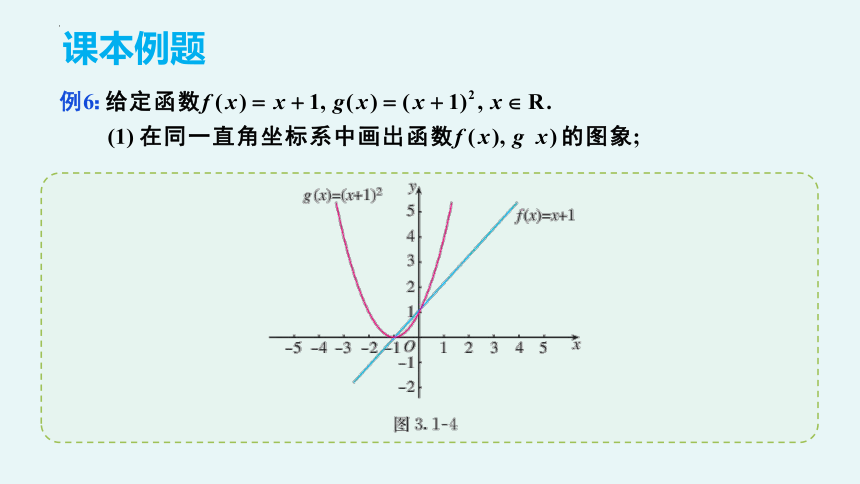
【例4】
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
课本例题
【例4】
函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.那么判断一个图形是不是函数图象的依据是什么?
课本例题
列表法 图象法 解析法
定义 用表格的形式把两个变量间的函数关系表示出来的方法 用图象把两个变量间的函数关系表示出来的方法 一个函数的对应关系可以用自变量的解析式表示出来的方法
优 点 不必通过计算就能直接看出与自变量的值相对应的函数值 可以直观形象地表示随着自变量的变化,相应的函数值变化的趋势,有利于研究函数的性质 简明全面的概括了变量之间的对应关系;通过解析式可以求出任意一个自变量的值所对应的函数值
缺 点 只能表示有限个元素的函数关系 有些函数的图象难以精确作出 一些实际问题难以找到它的解析式
【思考】比较函数的三种表示法,它们各有什么优点和缺点
【思考】所有函数都能用解析法表示吗?列表法与图像法呢?请你举出实例加以说明.
并不是所有函数都能用解析法表示.
(1)如某地一年中每天的最高气温是日期的函数,该函数就不能用解析法表示;
(2)同样,并不是所有的函数都能用图像法表示,如函数 不能用图像法表示;
(3)列表法虽在理论上适用于所有函数,但对于自变量有无限个取值的情况,列表法只能表示函数的一个概况或片段.
课本例题
对于函数,若自变量在定义域内的在不同范围取值时,函数的对应关系也不相同,则称函数叫分段函数.
注:
分段函数是一个函数,只是自变量在不同范围取值时,函数的对应关系不相同;
在书写时要指明各段函数自变量的取值范围;
分段函数的定义域是所以自变量取值区间的并集.
新知探究
课本例题
课本例题
1.如图,把直截面半径为25 cm的圆形木头锯成矩形木料,如果矩形的一边长为 x(单位:cm),面积为 y(单位:cm2),把 y 表示成 x 的函数.
25 cm
A
B
C
D
课本练习
2. 画出函数 的图象.
方法一:由绝对值的概念,可知 所以函数 的图像如图所示 .
方法二:(翻折法)先画出 的图像,然后再把图像中位于 x 轴下方的部分沿 x 轴翻折到 x 轴上面,其他不变.
方法三: 也可以由 y=|x| 的图象向右平移两个单位长度得到.
课本练习
1
2
3
4
1
2
O
y=|x-2|
x
y
课本练习
1
1
O
f(x)
x
y
g(x)
课本练习
1
1
O
m(x)
x
y
课本练习
分段函数的解析式问题
【典例】 已知函数f(x)=x2+1,g(x)=2x+4.若定义函数h(x):
当f(x)≥g(x)时,h(x)=f(x)-2g(x);当f(x)(1)写出h(x)的解析式;
(2)求h(h(g(-2)))的值.
审题策略:(1)由给出的h(x)的定义,通过解不等式得出自变量的两个不同取值区间,按照分段函数的形式写出解析式;
(2)由内向外逐步求值.
错因分析
规范展示:(1)当f(x)≥g(x),即x2+1≥2x+4时,解得x≤-1或x≥3,
此时h(x)=f(x)-2g(x)=x2+1-2(2x+4)=x2-4x-7;
当f(x)此时h(x)=2f(x)-g(x)=2(x2+1)-(2x+4)=2x2-2x-2.
(2)因为g(-2)=2×(-2)+4=0,
所以h(h(g(-2)))=h(h(0)),
而h(0)=2×02-2×0-2=-2,
所以h(h(g(-2)))=h(-2)=(-2)2-4×(-2)-7=5.
答题模板:第1步:由f(x)≥g(x)求得x的取值范围,并写出此时h(x)的解析式.
第2步:由f(x)
第3步:根据分段函数的形式写出h(x)的解析式.
第4步:先求g(-2)的值,再求h(g(-2))的值,最后求得h(h(g(-2)))的值.
失误展示
造成失分的原因主要如下:
(1)解错不等式,导致分段函数的分段范围错误;
(2)计算化简错误,导致h(x)的解析式错误;
(3)h(x)的结果不符合分段函数的要求;
(4)计算出错,导致结果错误.
【变式训练】 我国是水资源相对匮乏的国家,为鼓励节约用水,某市打算出台一项水费政策措施,规定每季度每人用水量不超过5吨时,每吨水费收基本价1.3元,当超过5吨而不超过6吨时,超过部分的水费加收200%,当超过6吨而不超过7吨时,超过部分的水费加收400%.如果某人本季度实际用水量为x(x≤7)吨,试计算,本季度他应缴多少水费
解:用y表示本季度应缴水费(单位:元).
当0当5第二部分由基本水费与加价水费组成,即1.3(x-5)+1.3(x-5)×200%=1.3(x-5)(1+200%),
则y2=1.3×5+1.3(x-5)(1+200%)=3.9x-13.
当6同理y3=1.3×5+1.3×(6-5)×(1+200%)+1.3(x-6)(1+400%)=6.5x-28.6.
典例剖析
总结归纳
总结归纳
注意定义域的端点是否取到,图象有实心点、空心点之分.
总结归纳
画含限制条件的函数图象的步骤
(1)画出初始函数的图象.
(2)根据已知的限制条件判断在每个范围内的图象是否符合题意.
(3)不在区域内的图象或不满足限制条件的图象改为虚线或不画.
总结归纳
总结归纳
总结归纳
函数的表示法
核心知识
方法总结
易错提醒
核心素养
求解析式的方法:
(1)待定系数法:函数类型已知时设出函数的一般式,然后利用条件求待定系数
(2)换元法:将含变量的代数式用新变量表示,进而求得解析式
(3)方程组法:根据已知条件构造方程组,进而求出函数解析式
(1)用换元法求函数的解析式时,要注意换元后自变量的取值范围
(2)用待定系数法求解析式是针对已知函数类型的问题
数学抽象:通过具体实例学习过程渗进归纳推理,培养数学抽象的核心素养
解析法
列表法
图象法
课堂小结
人教A版2019高一数学(必修一)第三章 函数的概念与性质
3.1.2函数的表示法(第1课时)
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
1.掌握函数的三种表示方法:解析法、图象法、列表法.(重点)
2.会根据不同的需要选择恰当的方法表示函数.(难点)
学习目标
Q1:由我们初中已经接触过了函数常见的三种表示方法,你还记得是哪三种方法吗?请结合教材P60--61的问题1,2,3,4来说明?
(1)解析法:用数学表达式表示两个变量之间的对应关系.
例如:问题1中的S=350t, t∈{t|0≤t≤0.5}
问题2中的w=350d, d∈{1,2,3,4,5}
(2)图象法:用图象表示两个变量之间的对应关系.
例如:问题3中的图象
情景导入
(3)列表法:用列出的表格来表示两个变量之间的对应关系.
例如:问题4中的表格
这三种方法是常用的函数表示法.
情景导入
【例4】
笔记本数x 1 2 3 4 5
钱数y 5 10 15 20 25
课本例题
【例4】
函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等.那么判断一个图形是不是函数图象的依据是什么?
课本例题
列表法 图象法 解析法
定义 用表格的形式把两个变量间的函数关系表示出来的方法 用图象把两个变量间的函数关系表示出来的方法 一个函数的对应关系可以用自变量的解析式表示出来的方法
优 点 不必通过计算就能直接看出与自变量的值相对应的函数值 可以直观形象地表示随着自变量的变化,相应的函数值变化的趋势,有利于研究函数的性质 简明全面的概括了变量之间的对应关系;通过解析式可以求出任意一个自变量的值所对应的函数值
缺 点 只能表示有限个元素的函数关系 有些函数的图象难以精确作出 一些实际问题难以找到它的解析式
【思考】比较函数的三种表示法,它们各有什么优点和缺点
【思考】所有函数都能用解析法表示吗?列表法与图像法呢?请你举出实例加以说明.
并不是所有函数都能用解析法表示.
(1)如某地一年中每天的最高气温是日期的函数,该函数就不能用解析法表示;
(2)同样,并不是所有的函数都能用图像法表示,如函数 不能用图像法表示;
(3)列表法虽在理论上适用于所有函数,但对于自变量有无限个取值的情况,列表法只能表示函数的一个概况或片段.
课本例题
对于函数,若自变量在定义域内的在不同范围取值时,函数的对应关系也不相同,则称函数叫分段函数.
注:
分段函数是一个函数,只是自变量在不同范围取值时,函数的对应关系不相同;
在书写时要指明各段函数自变量的取值范围;
分段函数的定义域是所以自变量取值区间的并集.
新知探究
课本例题
课本例题
1.如图,把直截面半径为25 cm的圆形木头锯成矩形木料,如果矩形的一边长为 x(单位:cm),面积为 y(单位:cm2),把 y 表示成 x 的函数.
25 cm
A
B
C
D
课本练习
2. 画出函数 的图象.
方法一:由绝对值的概念,可知 所以函数 的图像如图所示 .
方法二:(翻折法)先画出 的图像,然后再把图像中位于 x 轴下方的部分沿 x 轴翻折到 x 轴上面,其他不变.
方法三: 也可以由 y=|x| 的图象向右平移两个单位长度得到.
课本练习
1
2
3
4
1
2
O
y=|x-2|
x
y
课本练习
1
1
O
f(x)
x
y
g(x)
课本练习
1
1
O
m(x)
x
y
课本练习
分段函数的解析式问题
【典例】 已知函数f(x)=x2+1,g(x)=2x+4.若定义函数h(x):
当f(x)≥g(x)时,h(x)=f(x)-2g(x);当f(x)
(2)求h(h(g(-2)))的值.
审题策略:(1)由给出的h(x)的定义,通过解不等式得出自变量的两个不同取值区间,按照分段函数的形式写出解析式;
(2)由内向外逐步求值.
错因分析
规范展示:(1)当f(x)≥g(x),即x2+1≥2x+4时,解得x≤-1或x≥3,
此时h(x)=f(x)-2g(x)=x2+1-2(2x+4)=x2-4x-7;
当f(x)
(2)因为g(-2)=2×(-2)+4=0,
所以h(h(g(-2)))=h(h(0)),
而h(0)=2×02-2×0-2=-2,
所以h(h(g(-2)))=h(-2)=(-2)2-4×(-2)-7=5.
答题模板:第1步:由f(x)≥g(x)求得x的取值范围,并写出此时h(x)的解析式.
第2步:由f(x)
第3步:根据分段函数的形式写出h(x)的解析式.
第4步:先求g(-2)的值,再求h(g(-2))的值,最后求得h(h(g(-2)))的值.
失误展示
造成失分的原因主要如下:
(1)解错不等式,导致分段函数的分段范围错误;
(2)计算化简错误,导致h(x)的解析式错误;
(3)h(x)的结果不符合分段函数的要求;
(4)计算出错,导致结果错误.
【变式训练】 我国是水资源相对匮乏的国家,为鼓励节约用水,某市打算出台一项水费政策措施,规定每季度每人用水量不超过5吨时,每吨水费收基本价1.3元,当超过5吨而不超过6吨时,超过部分的水费加收200%,当超过6吨而不超过7吨时,超过部分的水费加收400%.如果某人本季度实际用水量为x(x≤7)吨,试计算,本季度他应缴多少水费
解:用y表示本季度应缴水费(单位:元).
当0
则y2=1.3×5+1.3(x-5)(1+200%)=3.9x-13.
当6
典例剖析
总结归纳
总结归纳
注意定义域的端点是否取到,图象有实心点、空心点之分.
总结归纳
画含限制条件的函数图象的步骤
(1)画出初始函数的图象.
(2)根据已知的限制条件判断在每个范围内的图象是否符合题意.
(3)不在区域内的图象或不满足限制条件的图象改为虚线或不画.
总结归纳
总结归纳
总结归纳
函数的表示法
核心知识
方法总结
易错提醒
核心素养
求解析式的方法:
(1)待定系数法:函数类型已知时设出函数的一般式,然后利用条件求待定系数
(2)换元法:将含变量的代数式用新变量表示,进而求得解析式
(3)方程组法:根据已知条件构造方程组,进而求出函数解析式
(1)用换元法求函数的解析式时,要注意换元后自变量的取值范围
(2)用待定系数法求解析式是针对已知函数类型的问题
数学抽象:通过具体实例学习过程渗进归纳推理,培养数学抽象的核心素养
解析法
列表法
图象法
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
