3.1.2函数的表示法(第2课时 分段函数) 课件(共53张PPT) -高一数学考试满分全攻略同步备课备考系列(人教A版2019必修一)
文档属性
| 名称 | 3.1.2函数的表示法(第2课时 分段函数) 课件(共53张PPT) -高一数学考试满分全攻略同步备课备考系列(人教A版2019必修一) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览







文档简介
(共53张PPT)
人教A版2019高一数学(必修一)第三章 函数的概念与性质
第2课时 分段函数
3.1.2函数的表示法
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
1.了解分段函数的概念,会求分段函数的函数值,能画出分段函数的图象.(重点,难点)
2.能在实际问题中列出分段函数,并能解决有关问题.(重点、难点)
学习目标
1.如何理解分段函数,处理分段函数问题的一般思路是怎样的?
注:分段函数是一个函数,只是自变量在不同范围取值时,函数的对应关系不相同.
分段函数:对于函数y= (x),若自变量在定义域内的在不同范围取值时,函数的对应关系也不相同,则称函数y= (x)叫分段函数.
2.函数常见的表示方法有哪几种?各有什么特点各是什么?
(1)解析法;(2)图象法;(3)列表法.
复习导入
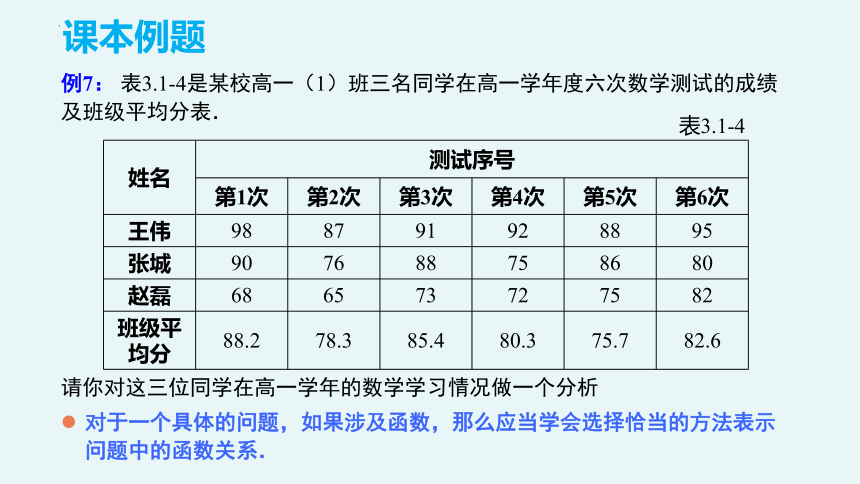
例7: 表3.1-4是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
姓名 测试序号
第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
请你对这三位同学在高一学年的数学学习情况做一个分析
对于一个具体的问题,如果涉及函数,那么应当学会选择恰当的方法表示问题中的函数关系.
表3.1-4
课本例题
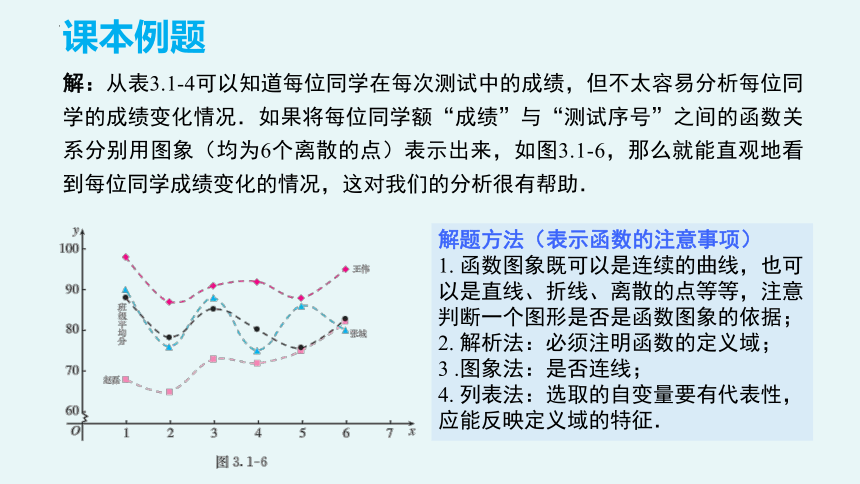
解:从表3.1-4可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将每位同学额“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,如图3.1-6,那么就能直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
解题方法(表示函数的注意事项)
1. 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等,注意判断一个图形是否是函数图象的依据;
2. 解析法:必须注明函数的定义域;
3 .图象法:是否连线;
4. 列表法:选取的自变量要有代表性,应能反映定义域的特征.
课本例题
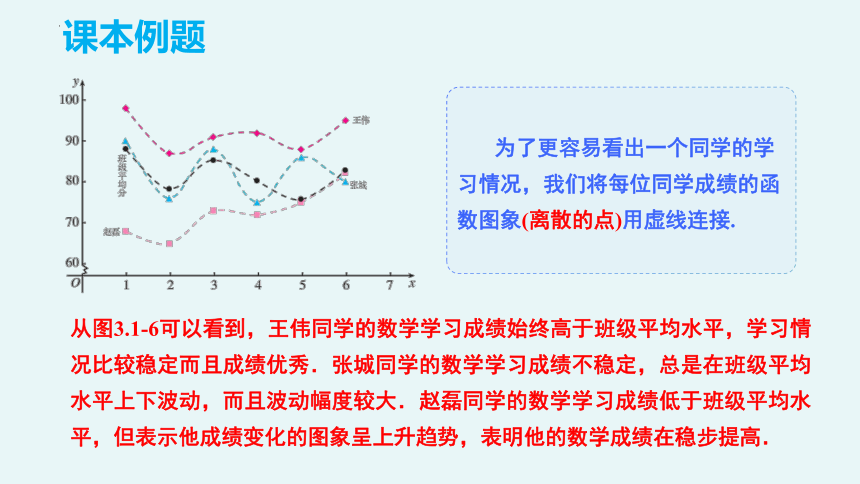
从图3.1-6可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
为了更容易看出一个同学的学习情况,我们将每位同学成绩的函数图象(离散的点)用虚线连接.
课本例题
例8. 依法纳税是每个公民应尽的义务,个人取得的所得应依照 《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除 -专项附扣除-依法确定的其他扣除.其中,“基本减除费用”(免征额)为每年60000元.税率与速算扣除数见下表.
级数 全年应纳税所得额所在区间 税率(0/0) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 16920
4 (300000,420000] 25 31920
5 (420000,660000] 30 52920
6 (660000,960000] 35 85920
7 (960000,+∞) 45 181920
课本例题
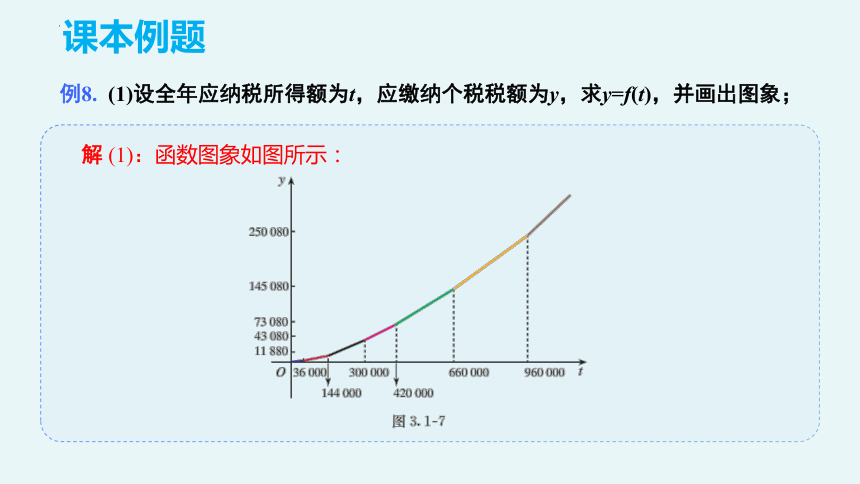
例8. (1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t),并画出图象;
解 (1):根据表,可得函数的解析式为:
课本例题
例8. (1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t),并画出图象;
解 (1):函数图象如图所示:
课本例题
例8. (2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其它扣除是4560元,那么他全年应缴纳多少综合所得税?
解 (2):根据,小王全年应纳税所得额为:
将的值代入(1)中,得.
所以,小王应缴纳得综合所得税税额为元.
课本例题
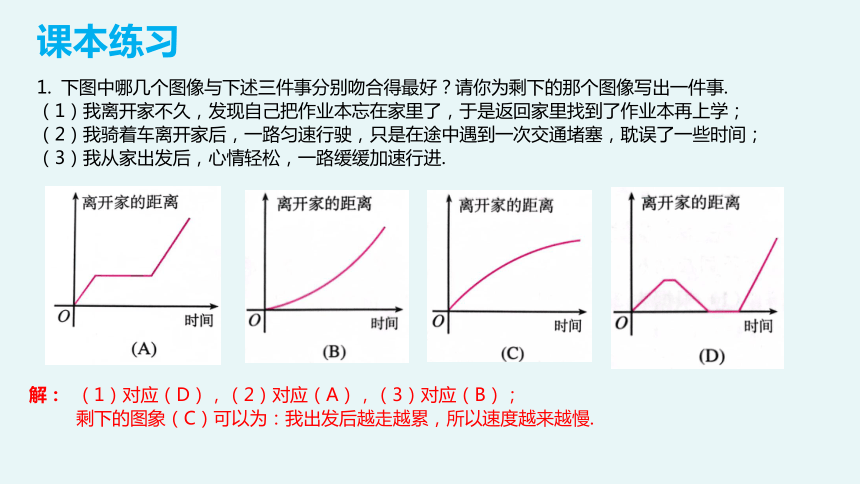
下图中哪几个图像与下述三件事分别吻合得最好?请你为剩下的那个图像写出一件事.
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车离开家后,一路匀速行驶,只是在途中遇到一次交通堵塞,耽误了一些时间;
(3)我从家出发后,心情轻松,一路缓缓加速行进.
解:
(1)对应(D),(2)对应(A),(3)对应(B);
剩下的图象(C)可以为:我出发后越走越累,所以速度越来越慢.
课本练习
2.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5 km以内(含5 km),票价2元;
(2)5 km以上,每增加5 km,票价增加1元(不足5 km的按5 km计算).
如果某条线路的总里程为20 km,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
根据这个解析式,可画出函数图象,如图所示.
课本练习
分段函数的解析式问题
【典例】 已知函数f(x)=x2+1,g(x)=2x+4.若定义函数h(x):
当f(x)≥g(x)时,h(x)=f(x)-2g(x);当f(x)(1)写出h(x)的解析式;
(2)求h(h(g(-2)))的值.
审题策略:(1)由给出的h(x)的定义,通过解不等式得出自变量的两个不同取值区间,按照分段函数的形式写出解析式;
(2)由内向外逐步求值.
错因分析
规范展示:(1)当f(x)≥g(x),即x2+1≥2x+4时,解得x≤-1或x≥3,
此时h(x)=f(x)-2g(x)=x2+1-2(2x+4)=x2-4x-7;
当f(x)此时h(x)=2f(x)-g(x)=2(x2+1)-(2x+4)=2x2-2x-2.
(2)因为g(-2)=2×(-2)+4=0,
所以h(h(g(-2)))=h(h(0)),
而h(0)=2×02-2×0-2=-2,
所以h(h(g(-2)))=h(-2)=(-2)2-4×(-2)-7=5.
答题模板:第1步:由f(x)≥g(x)求得x的取值范围,并写出此时h(x)的解析式.
第2步:由f(x)
第3步:根据分段函数的形式写出h(x)的解析式.
第4步:先求g(-2)的值,再求h(g(-2))的值,最后求得h(h(g(-2)))的值.
失误展示
造成失分的原因主要如下:
(1)解错不等式,导致分段函数的分段范围错误;
(2)计算化简错误,导致h(x)的解析式错误;
(3)h(x)的结果不符合分段函数的要求;
(4)计算出错,导致结果错误.
【变式训练】 我国是水资源相对匮乏的国家,为鼓励节约用水,某市打算出台一项水费政策措施,规定每季度每人用水量不超过5吨时,每吨水费收基本价1.3元,当超过5吨而不超过6吨时,超过部分的水费加收200%,当超过6吨而不超过7吨时,超过部分的水费加收400%.如果某人本季度实际用水量为x(x≤7)吨,试计算,本季度他应缴多少水费
解:用y表示本季度应缴水费(单位:元).
当0当5第二部分由基本水费与加价水费组成,即1.3(x-5)+1.3(x-5)×200%=1.3(x-5)(1+200%),
则y2=1.3×5+1.3(x-5)(1+200%)=3.9x-13.
当6同理y3=1.3×5+1.3×(6-5)×(1+200%)+1.3(x-6)(1+400%)=6.5x-28.6.
总结归纳
第t天 6 13 20 27
M/万股 34 27 20 13
总结归纳
总结归纳
总结归纳
总结归纳
习题3.1
1
2
3
1
2
3
x
y
O
图①
8
8
x
y
O
图②
-8
-8
5
4
5
x
y
O
图③
3
-2
x
y
O
图④
图1
1
x
f(x)
O
1 2 3 4 5 6
10
9
8
7
6
5
4
3
2
1
x
y
O
图2
8.如图,矩形的面积为10.如果矩形的长为x,宽为y,对角线为d,周长为l,那么你能获得关于这些量的哪些函数?
9.一个圆柱形容器的底部直径是d cm,高是h cm.现在以v cm3/s的速度向容器内注入某种溶液.求容器内溶液的高度x(单位:cm)关于注入溶液的时间t(单位:s)的函数解析式,并写出函数的定义域和值域.
10.一个老师用5分制对数学作业评分.一次作业中,第一小组的同学按座位
序号1,2,3,4,5,6的次序,得分依次为5,3,4,2,4,5.你会怎样表示这次作业的得分情况?用x,y分别表示序号和对应的得分,y是x的函数吗?如果是,那么它的定义域、值域和对应关系各是什么?
x 1 2 3 4 5 6
y 5 3 4 2 4 5
1
2
3
1
2
3
x
y
O
4
5
6
7
8
-3
-2
-1
-1
2
x
y
O
5
8
-3
-1
2
x
y
O
5
8
-3
-1
1
2
3
1
2
3
x
y
O
-3
-2
-1
-3
-2
-1
O
u
v
15.如图所示,一座小岛距离海岸线上最近的点P的距离是2 km,从点P沿海岸正东12 km处有一个城镇.
(1)假设一个人驾驶的小船的平均速度为3 km/h,步行的速度是5 km/h,t(单位:h)表示它从小岛到城镇的时间,x(单位:km)表示此人将船停在海岸处距点P的距离.请将t表示为x的函数.
(2)如果将船停在距点P 4 km处,那么从小岛到城镇要多长时间(精确到1h)
A
C
B
A
C
B
18.在一个展现人脑智力的综艺节目中,一位参加节目的少年能将圆周率π准确地记忆到小数点后面200位,更神奇的是,当主持人说出小数点后面的位数时,这位少年都能准确地说出该数位上的数字.如果记圆周率π小数点后第n位上的数字为y,那么你认为y是n的函数吗?如果是,请写出函数的定义域、值域与对应关系;如果不是,请说明理由.
已知函数值求字母的值的四个步骤
分段函数
核心知识
方法总结
易错提醒
核心素养
求值、作图、应用
(1)讨论:对字母的取值范围分类讨论.
(2)代入:由不同取值范围,代入对应的解析式中.
(3)求解:通过解方程求出字母的值.
(4)检验:检验所求的值是否在所讨论的区间内..
分段函数是一个函数,而不是几个函数
作分段函数图象时要注意衔接点的虚实
数学运算:通过分段函数的求值,培养数学运算的核心素养
课堂小结
人教A版2019高一数学(必修一)第三章 函数的概念与性质
第2课时 分段函数
3.1.2函数的表示法
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
1.了解分段函数的概念,会求分段函数的函数值,能画出分段函数的图象.(重点,难点)
2.能在实际问题中列出分段函数,并能解决有关问题.(重点、难点)
学习目标
1.如何理解分段函数,处理分段函数问题的一般思路是怎样的?
注:分段函数是一个函数,只是自变量在不同范围取值时,函数的对应关系不相同.
分段函数:对于函数y= (x),若自变量在定义域内的在不同范围取值时,函数的对应关系也不相同,则称函数y= (x)叫分段函数.
2.函数常见的表示方法有哪几种?各有什么特点各是什么?
(1)解析法;(2)图象法;(3)列表法.
复习导入
例7: 表3.1-4是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
姓名 测试序号
第1次 第2次 第3次 第4次 第5次 第6次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
请你对这三位同学在高一学年的数学学习情况做一个分析
对于一个具体的问题,如果涉及函数,那么应当学会选择恰当的方法表示问题中的函数关系.
表3.1-4
课本例题
解:从表3.1-4可以知道每位同学在每次测试中的成绩,但不太容易分析每位同学的成绩变化情况.如果将每位同学额“成绩”与“测试序号”之间的函数关系分别用图象(均为6个离散的点)表示出来,如图3.1-6,那么就能直观地看到每位同学成绩变化的情况,这对我们的分析很有帮助.
解题方法(表示函数的注意事项)
1. 函数图象既可以是连续的曲线,也可以是直线、折线、离散的点等等,注意判断一个图形是否是函数图象的依据;
2. 解析法:必须注明函数的定义域;
3 .图象法:是否连线;
4. 列表法:选取的自变量要有代表性,应能反映定义域的特征.
课本例题
从图3.1-6可以看到,王伟同学的数学学习成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学学习成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学学习成绩低于班级平均水平,但表示他成绩变化的图象呈上升趋势,表明他的数学成绩在稳步提高.
为了更容易看出一个同学的学习情况,我们将每位同学成绩的函数图象(离散的点)用虚线连接.
课本例题
例8. 依法纳税是每个公民应尽的义务,个人取得的所得应依照 《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税).2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为:个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为:应纳税所得额=综合所得收入额-基本减除费用-专项扣除 -专项附扣除-依法确定的其他扣除.其中,“基本减除费用”(免征额)为每年60000元.税率与速算扣除数见下表.
级数 全年应纳税所得额所在区间 税率(0/0) 速算扣除数
1 [0,36000] 3 0
2 (36000,144000] 10 2520
3 (144000,300000] 20 16920
4 (300000,420000] 25 31920
5 (420000,660000] 30 52920
6 (660000,960000] 35 85920
7 (960000,+∞) 45 181920
课本例题
例8. (1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t),并画出图象;
解 (1):根据表,可得函数的解析式为:
课本例题
例8. (1)设全年应纳税所得额为t,应缴纳个税税额为y,求y=f(t),并画出图象;
解 (1):函数图象如图所示:
课本例题
例8. (2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其它扣除是4560元,那么他全年应缴纳多少综合所得税?
解 (2):根据,小王全年应纳税所得额为:
将的值代入(1)中,得.
所以,小王应缴纳得综合所得税税额为元.
课本例题
下图中哪几个图像与下述三件事分别吻合得最好?请你为剩下的那个图像写出一件事.
(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;
(2)我骑着车离开家后,一路匀速行驶,只是在途中遇到一次交通堵塞,耽误了一些时间;
(3)我从家出发后,心情轻松,一路缓缓加速行进.
解:
(1)对应(D),(2)对应(A),(3)对应(B);
剩下的图象(C)可以为:我出发后越走越累,所以速度越来越慢.
课本练习
2.某市“招手即停”公共汽车的票价按下列规则制定:
(1)5 km以内(含5 km),票价2元;
(2)5 km以上,每增加5 km,票价增加1元(不足5 km的按5 km计算).
如果某条线路的总里程为20 km,请根据题意,写出票价与里程之间的函数解析式,并画出函数的图象.
根据这个解析式,可画出函数图象,如图所示.
课本练习
分段函数的解析式问题
【典例】 已知函数f(x)=x2+1,g(x)=2x+4.若定义函数h(x):
当f(x)≥g(x)时,h(x)=f(x)-2g(x);当f(x)
(2)求h(h(g(-2)))的值.
审题策略:(1)由给出的h(x)的定义,通过解不等式得出自变量的两个不同取值区间,按照分段函数的形式写出解析式;
(2)由内向外逐步求值.
错因分析
规范展示:(1)当f(x)≥g(x),即x2+1≥2x+4时,解得x≤-1或x≥3,
此时h(x)=f(x)-2g(x)=x2+1-2(2x+4)=x2-4x-7;
当f(x)
(2)因为g(-2)=2×(-2)+4=0,
所以h(h(g(-2)))=h(h(0)),
而h(0)=2×02-2×0-2=-2,
所以h(h(g(-2)))=h(-2)=(-2)2-4×(-2)-7=5.
答题模板:第1步:由f(x)≥g(x)求得x的取值范围,并写出此时h(x)的解析式.
第2步:由f(x)
第3步:根据分段函数的形式写出h(x)的解析式.
第4步:先求g(-2)的值,再求h(g(-2))的值,最后求得h(h(g(-2)))的值.
失误展示
造成失分的原因主要如下:
(1)解错不等式,导致分段函数的分段范围错误;
(2)计算化简错误,导致h(x)的解析式错误;
(3)h(x)的结果不符合分段函数的要求;
(4)计算出错,导致结果错误.
【变式训练】 我国是水资源相对匮乏的国家,为鼓励节约用水,某市打算出台一项水费政策措施,规定每季度每人用水量不超过5吨时,每吨水费收基本价1.3元,当超过5吨而不超过6吨时,超过部分的水费加收200%,当超过6吨而不超过7吨时,超过部分的水费加收400%.如果某人本季度实际用水量为x(x≤7)吨,试计算,本季度他应缴多少水费
解:用y表示本季度应缴水费(单位:元).
当0
则y2=1.3×5+1.3(x-5)(1+200%)=3.9x-13.
当6
总结归纳
第t天 6 13 20 27
M/万股 34 27 20 13
总结归纳
总结归纳
总结归纳
总结归纳
习题3.1
1
2
3
1
2
3
x
y
O
图①
8
8
x
y
O
图②
-8
-8
5
4
5
x
y
O
图③
3
-2
x
y
O
图④
图1
1
x
f(x)
O
1 2 3 4 5 6
10
9
8
7
6
5
4
3
2
1
x
y
O
图2
8.如图,矩形的面积为10.如果矩形的长为x,宽为y,对角线为d,周长为l,那么你能获得关于这些量的哪些函数?
9.一个圆柱形容器的底部直径是d cm,高是h cm.现在以v cm3/s的速度向容器内注入某种溶液.求容器内溶液的高度x(单位:cm)关于注入溶液的时间t(单位:s)的函数解析式,并写出函数的定义域和值域.
10.一个老师用5分制对数学作业评分.一次作业中,第一小组的同学按座位
序号1,2,3,4,5,6的次序,得分依次为5,3,4,2,4,5.你会怎样表示这次作业的得分情况?用x,y分别表示序号和对应的得分,y是x的函数吗?如果是,那么它的定义域、值域和对应关系各是什么?
x 1 2 3 4 5 6
y 5 3 4 2 4 5
1
2
3
1
2
3
x
y
O
4
5
6
7
8
-3
-2
-1
-1
2
x
y
O
5
8
-3
-1
2
x
y
O
5
8
-3
-1
1
2
3
1
2
3
x
y
O
-3
-2
-1
-3
-2
-1
O
u
v
15.如图所示,一座小岛距离海岸线上最近的点P的距离是2 km,从点P沿海岸正东12 km处有一个城镇.
(1)假设一个人驾驶的小船的平均速度为3 km/h,步行的速度是5 km/h,t(单位:h)表示它从小岛到城镇的时间,x(单位:km)表示此人将船停在海岸处距点P的距离.请将t表示为x的函数.
(2)如果将船停在距点P 4 km处,那么从小岛到城镇要多长时间(精确到1h)
A
C
B
A
C
B
18.在一个展现人脑智力的综艺节目中,一位参加节目的少年能将圆周率π准确地记忆到小数点后面200位,更神奇的是,当主持人说出小数点后面的位数时,这位少年都能准确地说出该数位上的数字.如果记圆周率π小数点后第n位上的数字为y,那么你认为y是n的函数吗?如果是,请写出函数的定义域、值域与对应关系;如果不是,请说明理由.
已知函数值求字母的值的四个步骤
分段函数
核心知识
方法总结
易错提醒
核心素养
求值、作图、应用
(1)讨论:对字母的取值范围分类讨论.
(2)代入:由不同取值范围,代入对应的解析式中.
(3)求解:通过解方程求出字母的值.
(4)检验:检验所求的值是否在所讨论的区间内..
分段函数是一个函数,而不是几个函数
作分段函数图象时要注意衔接点的虚实
数学运算:通过分段函数的求值,培养数学运算的核心素养
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
