3.3.1 从函数观点看一元二次方程 课件(共31张PPT)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一)
文档属性
| 名称 | 3.3.1 从函数观点看一元二次方程 课件(共31张PPT)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览










文档简介
(共31张PPT)
苏教版2019高一数学(必修一)第三章 不等式
3.3从函数观点看一元二次方程和一元二次不等式
3.3.1 从函数观点看一元二次方程
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
1.了解一元二次方程的根与二次函数零点的关系.
2.会用函数的图象判断一元二次方程的根的情况.
3.通过用二次函数的图象判断一元二次方程的根的情况,提升直观想象素养、逻辑推理素养.
情景导入
我们知道,一次函数、一元一次方程、一元一次不等式之间有着密切的联系. 例如,可以借助函数 y=2x-3 的图象来求解 2x-3=0,2x-3>0,2x-3<0.
反过来,也可以通过求解 2x-3=0,2x-3>0,
2x-3<0,来深人理解函数 y=2x-3的性质,那么
●怎样从函数观点进一步解决方程、不等式的问题
新知探究
从函数的观点看,方程 x2-2x-3=0的两个根 x1=-1,x2=3,就是二次函数 y=x2-2x-3 当函数值取零时自变量x的值,即二次函数 y=x2-2x-3 的图象与x轴交点的横坐标.
这时,我们称-1,3 为二次函数 y=x2-2x-3 的零点.
一、二次函数的零点
一般地,一元二次方程 ax2+bx+c=0 (a≠0) 的根就是二次函数 y=ax2+bx+c (a≠0) 当函数值取零时_______________,即二次函数 y=ax2+bx+c (a≠0) 的图象与______________________,也称为二次函数 y=ax2 +bx+c (a≠0)的零点.
自变量x的值
x轴交点的横坐标
归纳总结
二、一元二次方程 ax2+bx+c=0(a≠0)的根、
二次函数 y=ax2+bx+c(a≠0)的图象、
二次函数y=ax2+bx+c(a≠0)的零点之间的关系.
归纳总结
(1) 关系 (当a>0时).
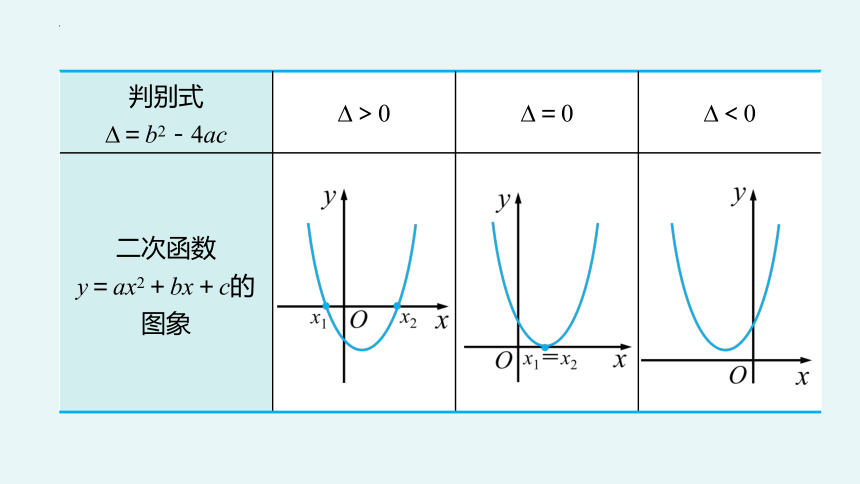
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,2= 有两个相等的实数根 x1=x2=- 没有实数根
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
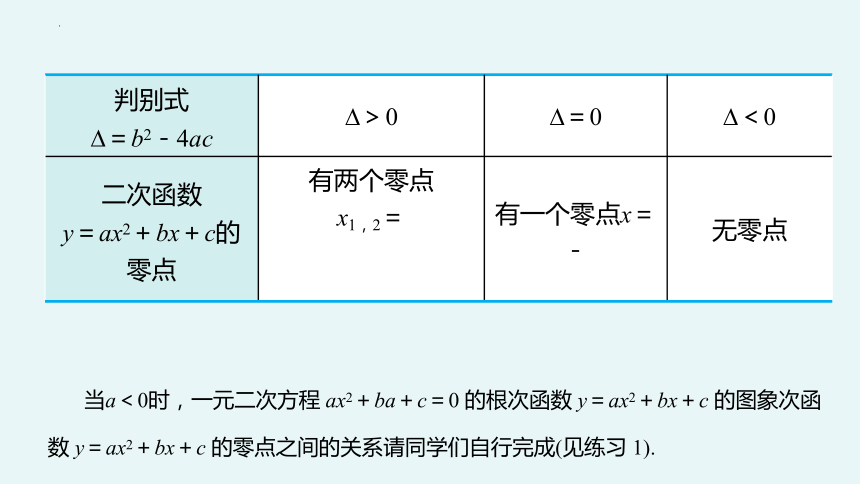
二次函数 y=ax2+bx+c的零点 有两个零点 x1,2= 有一个零点x=- 无零点
当a<0时,一元二次方程 ax2+ba+c=0 的根次函数 y=ax2+bx+c 的图象次函数 y=ax2+bx+c 的零点之间的关系请同学们自行完成(见练习 1).
例 1
求证:二次函数 y=2x2+3x-7 有两个零点.
分析 要证明二次函数 y=x2+3x-7 有两个零点,只需证明元二次方程 2x2+3x-7=0有两个不相等的实数根即可.
课本例题
证明:考察一元二次方程 2x2+3x-7=0.
因为 =32-4×2×(-7) =65>0,
所以方程 2x2+3x-7=0 有两个不相等的实数根.
因此,二次函数 y=2x2+3x-7有两个零点.
例 2
判断二次函数 y=x2-2x-1在区间(2,3)上是否存在零点.
解:根据求根公式可得一元二次方程 x2-2x-1=0 的两个根分别为
x1=1+,x2=1-.
因为 1< <2,
所以 1<1+< 3.
因此,二次函数y=x2-2x-1在区间(2,3)上存在零点.
课本例题
1. 当 a < 0 时,请填下表:
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,2= 有两个相等的实数根 x1=x2=- 没有实数根
课本练习
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的零点 有两个零点 x1,2= 有一个零点x=- 无零点
2. 画出二次函数 y=x2-x-2 的图象,并指出该函数的零点.
解:二次函数 y=x2-x-2 图象如下:
由 x2-x-2=0 得,x=-1或x=2.
故所求零点为-1,2.
3. 求下列二次函数的零点:
(1) y=(x+1)(x-1); (2) y=x2-4x;
解:令 y=0,得x1=-l,x2=1,
所以函数的零点为-1和 1.
解:令 y=0,即 x2-4x=0,得x(x-4)=0,
解得x1=0,x2=4,
所以函数的零点为 0 和 4 .
(3) y=-3x2-9; (4) y=-x2+2x-1.
解:令 y=-3x2-9=0,
方程无实数根,所以函数无零点.
解:令 y=-x2+2x-1=0,即x2-2x+1=0,
得 (x-1)2=0,解得 x=1.
所以函数的零点为1.
D
易错点 忽略对参数的分类讨论而致错
错因分析
C
一、选择题
1.函数y=-x2+x+2的零点个数是( )
A.0 B.1 C.2 D.3
解析 由-x2+x+2=0得Δ=1+8=9>0,
∴方程有两个实根,即函数有两个零点.
分层练习-基础
2.已知关于x的方程x2-ax+3=0的一个根大于1,另一个根小于1,则实数a的取值范围是( )
A.(4,+∞) B.(-∞,4)
C.(-∞,2) D.(2,+∞)
解析 ∵关于x的方程x2-ax+3=0的一个根大于1,另一个根小于1,
∴令y=x2-ax+3,其图象开口向上,
只需y|x=1=1-a+3=4-a<0,得a>4.
故选A.
A
3.若二次函数y=ax2+2x+1(a≠0)有一个正零点和一个负零点,则有( )
A.a<0 B.a>0 C.a<-1 D.a>1
解析 法一 由y=ax2+2x+1(a≠0)的图象过(0,1)点,知要使函数的图象与x轴的交点分别在y轴的左、右两侧,则a<0.
A
法二 由方程ax2+2x+1=0有两相异号实根,设两根为x1,x2,
C
4.若关于x的方程ax2+bx+c=0(a≠0)有两个实根1,2,则函数y=cx2+bx+a的零点为( )
解析 ∵1和2是ax2+bx+c=0的两根,
B
5.若二次函数y=ax2+bx+c(a≠0)满足y|x=1=0,且a>b>c,则该函数的零点个数为( )
A.1 B.2 C.0 D.不能确定
解析 由y|x=1=a+b+c=0,又a>b>c,
∴a>0,c<0,∴Δ=b2-4ac>0,
∴函数的零点有2个.
二、填空题
6.函数y=x2-mx-2的一个零点是-1,则m=________,另一个零点是________.
解析 由y|x=-1=1+m-2=0得m=1,
∴y=x2-x-2,由x2-x-2=0得x1=-1或x2=2.
1
2
7.已知函数y=ax2+2ax+c(a≠0)的一个零点为1,则它的另一个零点为________.
-3
解析 由题意知ax2+2ax+c=0的一个根为1,设另一根为x0.
则1+x0=-2,∴x0=-3.
0
8.函数y=x2-5x-6在区间[1,4]上的零点个数是________.
解析 由x2-5x-6=0得x1=-1,x2=6.
即函数的零点是-1,6,
∴函数在区间[1,4]上的零点个数为0.
三、解答题
9.已知二次函数y=-x2-x+a只有一个零点,求实数a的值.
解 二次函数y=-x2-x+a只有一个零点,即方程-x2-x+a=0有两个相等的实数根,
∴Δ=1+4a=0.
10.已知函数y=ax2+2ax+1有两个零点x1,x2且x1∈(0,1),x2∈(-4,-2),求实数a的取值范围.
解 ∵y=ax2+2ax+1有两个零点,则函数的图象过(0,1)且与x轴有两个交点,又x1∈(0,1),x2∈(-4,-2),
11.若函数y=ax2-2(a+1)x+a-1有且仅有一个零点,则实数a=___________.
当a≠0时,ax2-2(a+1)x+a-1=0为一元二次方程,且有两个相等的实数根,
分层练习-巩固
B
12.在R上定义运算⊙:a⊙b=ab+2a+b,则y=x⊙(x-2)的零点为( )
A.0和2 B.-2和1
C.-1和2 D.-2和0
解析 由题意y=x(x-2)+2x+(x-2)=x2+x-2=(x+2)(x-1),
令y=0,
∴x=-2或x=1.
13.若二次函数y=x2+2x-m+1没有零点,试说明关于x的方程x2+mx+12m=1一定有实数根.
解 由题意知,关于x的方程x2+2x-m+1=0没有实数根,
∴此方程的判别式Δ=22-4×1×(-m+1)<0,解得m<0.
而方程x2+mx+12m=1的根的判别式
Δ′=m2-4×1×(12m-1)=m2-48m+4,
∵m<0,∴m2>0,-48m>0,
∴m2-48m+4>0,即Δ′>0,
∴方程x2+mx+12m=1有两个不相等的实数根,即一定有实数根.
ABD
14.(多选题)函数y1=(x-2)(x-5)-1有两个零点x1,x2,且x1A.x1<2且22且x2>5
C.x1<2且x2>5 D.25
解析 令y2=(x-2)(x-5),则y1=y2-1,
∴函数y1=(x-2)(x-5)-1的零点就是函数y2=(x-2)·(x-5)与函数y=1图象的交点的横坐标.
在同一坐标系内画出y2=(x-2)(x-5)的图象与
y=1的图象如图所示,结合图象知只有C正确.
分层练习-拓展
1.掌握1个概念——函数的零点
二次函数y=ax2+bx+c(a≠0)的零点就是方程y=0的实数根,也就是二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标,所以函数的零点是一个数而不是一个点,在写函数零点时,所写的一定是一个数,而不是一个坐标.
2.提升1个素养——数形结合
结合二次函数图象理解一元二次方程的根与函数的零点的关系.
课堂小结
苏教版2019高一数学(必修一)第三章 不等式
3.3从函数观点看一元二次方程和一元二次不等式
3.3.1 从函数观点看一元二次方程
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
1.了解一元二次方程的根与二次函数零点的关系.
2.会用函数的图象判断一元二次方程的根的情况.
3.通过用二次函数的图象判断一元二次方程的根的情况,提升直观想象素养、逻辑推理素养.
情景导入
我们知道,一次函数、一元一次方程、一元一次不等式之间有着密切的联系. 例如,可以借助函数 y=2x-3 的图象来求解 2x-3=0,2x-3>0,2x-3<0.
反过来,也可以通过求解 2x-3=0,2x-3>0,
2x-3<0,来深人理解函数 y=2x-3的性质,那么
●怎样从函数观点进一步解决方程、不等式的问题
新知探究
从函数的观点看,方程 x2-2x-3=0的两个根 x1=-1,x2=3,就是二次函数 y=x2-2x-3 当函数值取零时自变量x的值,即二次函数 y=x2-2x-3 的图象与x轴交点的横坐标.
这时,我们称-1,3 为二次函数 y=x2-2x-3 的零点.
一、二次函数的零点
一般地,一元二次方程 ax2+bx+c=0 (a≠0) 的根就是二次函数 y=ax2+bx+c (a≠0) 当函数值取零时_______________,即二次函数 y=ax2+bx+c (a≠0) 的图象与______________________,也称为二次函数 y=ax2 +bx+c (a≠0)的零点.
自变量x的值
x轴交点的横坐标
归纳总结
二、一元二次方程 ax2+bx+c=0(a≠0)的根、
二次函数 y=ax2+bx+c(a≠0)的图象、
二次函数y=ax2+bx+c(a≠0)的零点之间的关系.
归纳总结
(1) 关系 (当a>0时).
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,2= 有两个相等的实数根 x1=x2=- 没有实数根
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的零点 有两个零点 x1,2= 有一个零点x=- 无零点
当a<0时,一元二次方程 ax2+ba+c=0 的根次函数 y=ax2+bx+c 的图象次函数 y=ax2+bx+c 的零点之间的关系请同学们自行完成(见练习 1).
例 1
求证:二次函数 y=2x2+3x-7 有两个零点.
分析 要证明二次函数 y=x2+3x-7 有两个零点,只需证明元二次方程 2x2+3x-7=0有两个不相等的实数根即可.
课本例题
证明:考察一元二次方程 2x2+3x-7=0.
因为 =32-4×2×(-7) =65>0,
所以方程 2x2+3x-7=0 有两个不相等的实数根.
因此,二次函数 y=2x2+3x-7有两个零点.
例 2
判断二次函数 y=x2-2x-1在区间(2,3)上是否存在零点.
解:根据求根公式可得一元二次方程 x2-2x-1=0 的两个根分别为
x1=1+,x2=1-.
因为 1< <2,
所以 1<1+< 3.
因此,二次函数y=x2-2x-1在区间(2,3)上存在零点.
课本例题
1. 当 a < 0 时,请填下表:
判别式 =b2-4ac >0 =0 <0
方程 ax2+bx+c=0的根 有两个相异的实数根 x1,2= 有两个相等的实数根 x1=x2=- 没有实数根
课本练习
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的图象
判别式 =b2-4ac >0 =0 <0
二次函数 y=ax2+bx+c的零点 有两个零点 x1,2= 有一个零点x=- 无零点
2. 画出二次函数 y=x2-x-2 的图象,并指出该函数的零点.
解:二次函数 y=x2-x-2 图象如下:
由 x2-x-2=0 得,x=-1或x=2.
故所求零点为-1,2.
3. 求下列二次函数的零点:
(1) y=(x+1)(x-1); (2) y=x2-4x;
解:令 y=0,得x1=-l,x2=1,
所以函数的零点为-1和 1.
解:令 y=0,即 x2-4x=0,得x(x-4)=0,
解得x1=0,x2=4,
所以函数的零点为 0 和 4 .
(3) y=-3x2-9; (4) y=-x2+2x-1.
解:令 y=-3x2-9=0,
方程无实数根,所以函数无零点.
解:令 y=-x2+2x-1=0,即x2-2x+1=0,
得 (x-1)2=0,解得 x=1.
所以函数的零点为1.
D
易错点 忽略对参数的分类讨论而致错
错因分析
C
一、选择题
1.函数y=-x2+x+2的零点个数是( )
A.0 B.1 C.2 D.3
解析 由-x2+x+2=0得Δ=1+8=9>0,
∴方程有两个实根,即函数有两个零点.
分层练习-基础
2.已知关于x的方程x2-ax+3=0的一个根大于1,另一个根小于1,则实数a的取值范围是( )
A.(4,+∞) B.(-∞,4)
C.(-∞,2) D.(2,+∞)
解析 ∵关于x的方程x2-ax+3=0的一个根大于1,另一个根小于1,
∴令y=x2-ax+3,其图象开口向上,
只需y|x=1=1-a+3=4-a<0,得a>4.
故选A.
A
3.若二次函数y=ax2+2x+1(a≠0)有一个正零点和一个负零点,则有( )
A.a<0 B.a>0 C.a<-1 D.a>1
解析 法一 由y=ax2+2x+1(a≠0)的图象过(0,1)点,知要使函数的图象与x轴的交点分别在y轴的左、右两侧,则a<0.
A
法二 由方程ax2+2x+1=0有两相异号实根,设两根为x1,x2,
C
4.若关于x的方程ax2+bx+c=0(a≠0)有两个实根1,2,则函数y=cx2+bx+a的零点为( )
解析 ∵1和2是ax2+bx+c=0的两根,
B
5.若二次函数y=ax2+bx+c(a≠0)满足y|x=1=0,且a>b>c,则该函数的零点个数为( )
A.1 B.2 C.0 D.不能确定
解析 由y|x=1=a+b+c=0,又a>b>c,
∴a>0,c<0,∴Δ=b2-4ac>0,
∴函数的零点有2个.
二、填空题
6.函数y=x2-mx-2的一个零点是-1,则m=________,另一个零点是________.
解析 由y|x=-1=1+m-2=0得m=1,
∴y=x2-x-2,由x2-x-2=0得x1=-1或x2=2.
1
2
7.已知函数y=ax2+2ax+c(a≠0)的一个零点为1,则它的另一个零点为________.
-3
解析 由题意知ax2+2ax+c=0的一个根为1,设另一根为x0.
则1+x0=-2,∴x0=-3.
0
8.函数y=x2-5x-6在区间[1,4]上的零点个数是________.
解析 由x2-5x-6=0得x1=-1,x2=6.
即函数的零点是-1,6,
∴函数在区间[1,4]上的零点个数为0.
三、解答题
9.已知二次函数y=-x2-x+a只有一个零点,求实数a的值.
解 二次函数y=-x2-x+a只有一个零点,即方程-x2-x+a=0有两个相等的实数根,
∴Δ=1+4a=0.
10.已知函数y=ax2+2ax+1有两个零点x1,x2且x1∈(0,1),x2∈(-4,-2),求实数a的取值范围.
解 ∵y=ax2+2ax+1有两个零点,则函数的图象过(0,1)且与x轴有两个交点,又x1∈(0,1),x2∈(-4,-2),
11.若函数y=ax2-2(a+1)x+a-1有且仅有一个零点,则实数a=___________.
当a≠0时,ax2-2(a+1)x+a-1=0为一元二次方程,且有两个相等的实数根,
分层练习-巩固
B
12.在R上定义运算⊙:a⊙b=ab+2a+b,则y=x⊙(x-2)的零点为( )
A.0和2 B.-2和1
C.-1和2 D.-2和0
解析 由题意y=x(x-2)+2x+(x-2)=x2+x-2=(x+2)(x-1),
令y=0,
∴x=-2或x=1.
13.若二次函数y=x2+2x-m+1没有零点,试说明关于x的方程x2+mx+12m=1一定有实数根.
解 由题意知,关于x的方程x2+2x-m+1=0没有实数根,
∴此方程的判别式Δ=22-4×1×(-m+1)<0,解得m<0.
而方程x2+mx+12m=1的根的判别式
Δ′=m2-4×1×(12m-1)=m2-48m+4,
∵m<0,∴m2>0,-48m>0,
∴m2-48m+4>0,即Δ′>0,
∴方程x2+mx+12m=1有两个不相等的实数根,即一定有实数根.
ABD
14.(多选题)函数y1=(x-2)(x-5)-1有两个零点x1,x2,且x1
C.x1<2且x2>5 D.2
解析 令y2=(x-2)(x-5),则y1=y2-1,
∴函数y1=(x-2)(x-5)-1的零点就是函数y2=(x-2)·(x-5)与函数y=1图象的交点的横坐标.
在同一坐标系内画出y2=(x-2)(x-5)的图象与
y=1的图象如图所示,结合图象知只有C正确.
分层练习-拓展
1.掌握1个概念——函数的零点
二次函数y=ax2+bx+c(a≠0)的零点就是方程y=0的实数根,也就是二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标,所以函数的零点是一个数而不是一个点,在写函数零点时,所写的一定是一个数,而不是一个坐标.
2.提升1个素养——数形结合
结合二次函数图象理解一元二次方程的根与函数的零点的关系.
课堂小结
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
