3.3.2 从函数观点看一元二次不等式(第1课时 一元二次不等式的解法)(教学课件)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一)
文档属性
| 名称 | 3.3.2 从函数观点看一元二次不等式(第1课时 一元二次不等式的解法)(教学课件)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览











文档简介
苏教版2019高一数学(必修一)第三章 不等式
第一课时 一元二次不等式的解法
3.3.2 从函数观点看一元二次不等式
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
1.理解一元二次方程、二次函数、一元二次不等式的关系.
2.能借助二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集.
3.从函数观点认识不等式,感悟数学知识之间的关联,认识函数的重要性,重点提升数学抽象和数学运算素养.
我们来看下面的问题:
某杂志以每册 2 元的价格发行时,发行量为 10 万册经过调查若单册价格每提高 0.2 元,则发行量就减少 5000 册要使杂志社的销售收入大于 22.4 万元,每册杂志的价格应定在怎样的范围内?
设每册杂志价格提高 x 元,则发行量减少0.5×????0.2=5????2万册,杂志社的销售收人为
(2+x)(10-5????2)万元.
根据题意,得 (2+x)(10-5????2) >22.4,
化简,得 5x2-10x+4.8 < 0.
?
情景导入
一、一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是 2 的_______________叫作一元二次不等式.
整式不等式
我们知道,一元二次方程和相应的二次函数有着密切的联系,一元二次方程的根就是相应二次函数的图象与x轴交点的横坐标.那么,
● 一元二次不等式和相应的二次函数是否也有内在的联系?
新知探究
二、一元二次不等式和相应的二次函数的对应关系
(1) 关系:(a>0)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}判别式
?=b2-4ac
?>0
?=0
?<0
方程
ax2+bx+c=0的根
有两个相异的实数根
x1,x2 (x1<x2)
有两个相等的实数根
x1=x2=-????2????
没有实数根
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}判别式
?=b2-4ac
?>0
?=0
?<0
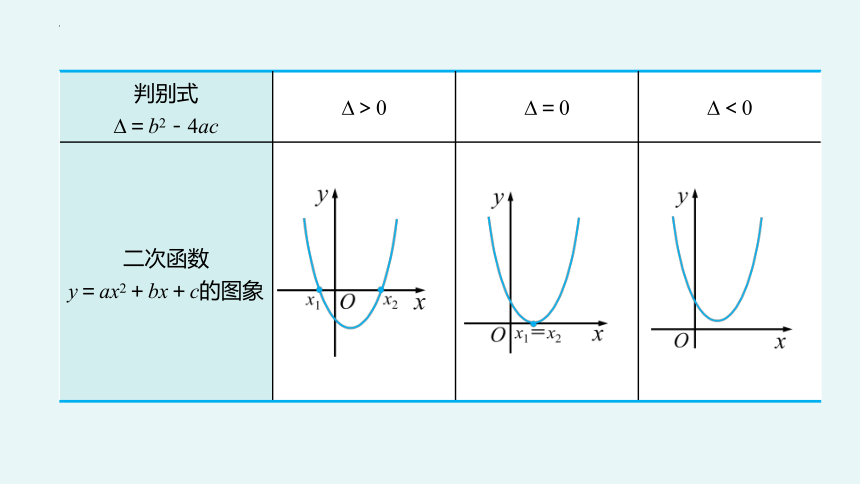
二次函数
y=ax2+bx+c的图象
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}判别式
?=b2-4ac
?>0
?=0
?<0
ax2+bx+c>0的解集
(-∞,x1)
∪
(x2,+∞)
(-∞,-????2????) ∪
(-????2????,+∞)
R
ax2+bx+c<0的解集
(x1<x2)
?
?
当a<0 时,通过不等式两边同乘以-1,可将问题转化为二次项系数为正的情形,利用表上表解决.
例 1
解下列不等式:
(1) x2-7x+12>0;
(2) -x2-2x+3≥0;
课本例题
解 方程 x2-7x+12=0 的解为
x1=3,x2=4.
根据 y=x2-7x+12 的图象
可得原不等式的{ x∣x<3 或 x>4}.
解 不等式两边同乘以-1,得 x2+2x-3≤0.
对 于二次项系数为负数的不等式,可以先把二次项系数化成正数,然后再求解.
方程 x2+2x-3=0 的解为 x1=-3,x2=1.
根据 y = x2+2x-3 的图象,
可得原不等式的解集为 { x∣-3≤x≤1).
(3) x2-2x+1<0;
解 方程 x2-2x+1=0
有两个相同的解x1=x2=1.
根据 y=x2-2x+1的图象,
可得原不等式的解集为?.
(4) x2-2x+2>0.
解 因为?<0,所以方程 x2-2x+2=0
无实数解.
根据 y=x2-2x+2 的图象,
可得原不等式的解集为 R .
1. (1) 不等式(x-1)(x-3)>0的解集为( )。
A.{ x∣x<1} B.{ x∣x>3}
C.{ x∣x<1 或 x>3} D.{ x∣1<x<3}
(2) 不等式-x2+2x-4>0 的解集为( ).
A. R B. ?
C. { x∣x>0,x∈R} D.{ x∣x<0,x∈R}.
C
B
课本练习
2. 解下列不等式:
(1) x2+4x-12>0;
解:该不等式可化为(x+6)(x-2)>0,
解得 x<-6或 x>2,
故原不等式的解集为
{ x∣x<-6 或 x>2}.
(2) x2-x+1≤0;
解:该不等式可化为(x-12)2+34≤0 ,
无解,
故原不等式的解集为?.
?
(3) 2x2-5x+3<0;
解:该不等式可化为
(x-1)(2x-3) <0,
解得 1<x< 32?,
故原不等式的解集为
{ x∣ 1<x< 32}.
?
(4) 3x2-x-4>0;
解:该不等式可化为
(x+1)(3x-4) >0,
解得 x<-1或 x> 43?,
故原不等式的解集为
{ x∣ x<-1或 x> 43}.
?
(5) 2x2+4x+3>0;
解:该不等式可化为
2(x+1)2+1>0,
恒成立,
故原不等式的解集为R.
(6) 9x2-6x+1≤0.
解:该不等式可化为(3x-1)2 ≤0,
解得 x=13,
故原不等式的解集为{ x∣x=13 }.
?
3. 解下列不等式:
(1) -6x2-x+2<0;
解:不等式可变形为
6x2+x-2>0 ,
对应方程的两根分别为12和-23,
由 y=6x2+x-2的图象知解集为
{ x∣x <-23 或 x>12 }
?
(2) 1-4x2≥4x+2;
解:不等式可变形为4x2+4x+1<0,
即(2x+1)2<0,
显然无解,
即解集为?.
(3) 1-3x<x2;
解:不等式可变形为
x2+3x-1>0,
对应方程的两根为
x1,2=-3±9+42= -3±132,
由 y=x2+3x-1的图象知解集为
{ x∣x < -3-132 或 x > -3+132 }.
?
(4) (x-2)(x+2) >1.
解:不等式可变形为 x2-5>0,
对应方程的两根为
x1=-5,x2=5,
由 y=x2-5 的图象知解集为
{ x∣x<-5 或 x>5 }.
?
4. 当 x 是什么实数时,函数 y=-x2+5x+14 的值是:
(1) 0?
解: -x2+5x+14=0
x2-5x-14=0
(x-7)(x+2) =0
x1=7,x2=-2
(2) 正数?
解: -x2+5x+14>0
x2-5x-14<0
(x-7)(x+2) <0
-2<x<7
(3) 负数?
解: -x2+5x+14<0
x2-5x-14>0
(x-7)(x+2) >0
x>7 或 x<-2.
5. (1)已知集合 M={x|-4≤x≤7,N={x|x2-x-6>0}, 求M∩N;
解:∵集合M = {x∣-4≤x≤7},
N = {x|x2-x-6>0}
= {x∣x<-2或 x>3},
∴ M∩N ={x∣-4≤x<-2 或 3< x≤7};
(2) 已知集合 A={x|x2-4x+3<0},B={x|(x-2)(x-5) <0},求 A∪B.
解:∵集合A={x|x2-4x+3<0}
={x∣1<x<3},
B={x|(x-2)(x-5)<0}
={x∣2<x<5},
∴ A∪B ={x∣1<x<5}.
错因分析
易错点 随意消项致错
A
一、选择题
1.不等式6x2+x-2≤0的解集为( )
解析 因为6x2+x-2≤0?(2x-1)(3x+2)≤0,
分层练习-基础
D
3.如果关于x的不等式x2 A.-81 B.81 C.-64 D.64
解析 不等式x2B
故1和3是x2-ax-b=0的两根,
解得a=4,b=-3.
所以ba=(-3)4=81.故选B.
B
4.在R上定义运算“⊙”:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
A.{x|0 C.{x|x<-2或x>1} D.{x|-1 解析 根据给出的定义得,
x⊙(x-2)=x(x-2)+2x+(x-2)=x2+x-2=(x+2)(x-1),
又x⊙(x-2)<0,
则(x+2)(x-1)<0,
故不等式的解集是{x|-2A
5.若一元二次不等式ax2+bx+c<0的解集为{x|x<-3或x>5},则ax2-bx+c<0的解集为( )
A.{x|x<-5或x>3} B.{x|-5 C.{x|x<-3或x>5} D.{x|-3 解析 由题意知-3和5是ax2+bx+c=0的两根,
由根与系数的关系得:
代入得ax2+2ax-15a<0,
又由解集的形式知a<0,∴x2+2x-15>0,
∴(x-3)(x+5)>0
∴x>3或x<-5.
4
故a+b=4.
7.不等式-1 解析 由-1<x2+2x-1≤2,
{x|-3≤x<-2或0 ∴-3≤x<-2或0 8.若一元二次方程ax2+bx+c=0的两根为2,-1,则当a<0时,不等式
ax2+bx+c≥0的解集为_______________.
[-1,2]
解析 由题意ax2+bx+c=a(x-2)(x+1),
故原不等式可化为a(x-2)(x+1)≥0,
又∵a<0,∴(x-2)(x+1)≤0,
所求解集为[-1,2].
三、解答题
9.解下列不等式:
(1)2x2+5x-3<0;(2)-3x2+6x≤2;
(2)原不等式等价于3x2-6x+2≥0.
(3)4x2-4x+1>0;(4)-x2+6x-10>0.
作出函数y=4x2-4x+1的图象如图③.
③
(4)原不等式可化为x2-6x+10<0,
∵Δ=36-40=-4<0,
∴方程x2-6x+10=0无实根,
∴原不等式的解集为?.
10.已知不等式x2+x-6<0的解集为A,不等式x2-2x-3<0的解集为B.
(1)求A∩B;
(2)若不等式x2+ax+b<0的解集为A∩B,求不等式ax2+bx+3<0的解集.
解 (1)由x2+x-6<0得-3 ∴A={x|-3 ∴B={x|-1 (2)由已知得-1和2为x2+ax+b=0的两根,
∴不等式ax2+bx+3<0为-x2-2x+3<0,即x2+2x-3>0,
解得x<-3或x>1.
∴所求不等式的解集为{x|x<-3或x>1}.
BC
11.(多选题)下列不等式的解集为R的是( )
B中,Δ=62-4×10<0,解集为R;
C中,不等式可化为x2-x+2>0,Δ=(-1)2-4×2<0,解集为R;
D中不等式化为2x2-3x+3<0,Δ=(-3)2+4×2×3<0,解集为?.
分层练习-巩固
∴m的取值范围是{m|m<0}.
(-∞,0)
13.解关于x的不等式x2-(a+a2)x+a3>0(a∈R).
解 原不等式可化为(x-a)(x-a2)>0.
当a<0时,aa2};
当a=0时,a2=a,原不等式的解集为{x|x≠0,x∈R};
当0a};
当a=1时,a2=a,原不等式的解集为{x|x≠1,x∈R};
当a>1时,aa2}.
综上所述,当a<0或a>1时,原不等式的解集为{x|xa2};
当0a};
当a=1时,原不等式的解集为{x|x≠1,x∈R};
当a=0时,原不等式的解集为{x|x≠0,x∈R}.
又f(1)=a-b+c>0,f(-1)=a+b+c<0,
作出函数y=ax2-bx+c的简图如图.
③⑤
∴b<0,而f(0)=c>0,
故③⑤正确.
分层练习-拓展
1.掌握1个知识点——一元二次不等式的解法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集.
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m<n时,若(x-m)(x-n)>0,则可得{x|x>n或x<m};若(x-m)(x-n)<0,则可得{x|m<x<n}.
有口诀如下:大于取两边,小于取中间.
课堂小结
2.突破1个重难点——含参数的一元二次不等式的解法
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”,讨论需从如下三个方面进行考虑
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:两根(Δ>0),一根(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,x1=x2,x1<x2.
3.规避1个易误点
当二次项系数小于0时,需两边同乘-1,化为正的.
课堂小结
第一课时 一元二次不等式的解法
3.3.2 从函数观点看一元二次不等式
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
1.理解一元二次方程、二次函数、一元二次不等式的关系.
2.能借助二次函数求解一元二次不等式,并能用集合表示一元二次不等式的解集.
3.从函数观点认识不等式,感悟数学知识之间的关联,认识函数的重要性,重点提升数学抽象和数学运算素养.
我们来看下面的问题:
某杂志以每册 2 元的价格发行时,发行量为 10 万册经过调查若单册价格每提高 0.2 元,则发行量就减少 5000 册要使杂志社的销售收入大于 22.4 万元,每册杂志的价格应定在怎样的范围内?
设每册杂志价格提高 x 元,则发行量减少0.5×????0.2=5????2万册,杂志社的销售收人为
(2+x)(10-5????2)万元.
根据题意,得 (2+x)(10-5????2) >22.4,
化简,得 5x2-10x+4.8 < 0.
?
情景导入
一、一元二次不等式的概念
只含有一个未知数,并且未知数最高次数是 2 的_______________叫作一元二次不等式.
整式不等式
我们知道,一元二次方程和相应的二次函数有着密切的联系,一元二次方程的根就是相应二次函数的图象与x轴交点的横坐标.那么,
● 一元二次不等式和相应的二次函数是否也有内在的联系?
新知探究
二、一元二次不等式和相应的二次函数的对应关系
(1) 关系:(a>0)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}判别式
?=b2-4ac
?>0
?=0
?<0
方程
ax2+bx+c=0的根
有两个相异的实数根
x1,x2 (x1<x2)
有两个相等的实数根
x1=x2=-????2????
没有实数根
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}判别式
?=b2-4ac
?>0
?=0
?<0
二次函数
y=ax2+bx+c的图象
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}判别式
?=b2-4ac
?>0
?=0
?<0
ax2+bx+c>0的解集
(-∞,x1)
∪
(x2,+∞)
(-∞,-????2????) ∪
(-????2????,+∞)
R
ax2+bx+c<0的解集
(x1<x2)
?
?
当a<0 时,通过不等式两边同乘以-1,可将问题转化为二次项系数为正的情形,利用表上表解决.
例 1
解下列不等式:
(1) x2-7x+12>0;
(2) -x2-2x+3≥0;
课本例题
解 方程 x2-7x+12=0 的解为
x1=3,x2=4.
根据 y=x2-7x+12 的图象
可得原不等式的{ x∣x<3 或 x>4}.
解 不等式两边同乘以-1,得 x2+2x-3≤0.
对 于二次项系数为负数的不等式,可以先把二次项系数化成正数,然后再求解.
方程 x2+2x-3=0 的解为 x1=-3,x2=1.
根据 y = x2+2x-3 的图象,
可得原不等式的解集为 { x∣-3≤x≤1).
(3) x2-2x+1<0;
解 方程 x2-2x+1=0
有两个相同的解x1=x2=1.
根据 y=x2-2x+1的图象,
可得原不等式的解集为?.
(4) x2-2x+2>0.
解 因为?<0,所以方程 x2-2x+2=0
无实数解.
根据 y=x2-2x+2 的图象,
可得原不等式的解集为 R .
1. (1) 不等式(x-1)(x-3)>0的解集为( )。
A.{ x∣x<1} B.{ x∣x>3}
C.{ x∣x<1 或 x>3} D.{ x∣1<x<3}
(2) 不等式-x2+2x-4>0 的解集为( ).
A. R B. ?
C. { x∣x>0,x∈R} D.{ x∣x<0,x∈R}.
C
B
课本练习
2. 解下列不等式:
(1) x2+4x-12>0;
解:该不等式可化为(x+6)(x-2)>0,
解得 x<-6或 x>2,
故原不等式的解集为
{ x∣x<-6 或 x>2}.
(2) x2-x+1≤0;
解:该不等式可化为(x-12)2+34≤0 ,
无解,
故原不等式的解集为?.
?
(3) 2x2-5x+3<0;
解:该不等式可化为
(x-1)(2x-3) <0,
解得 1<x< 32?,
故原不等式的解集为
{ x∣ 1<x< 32}.
?
(4) 3x2-x-4>0;
解:该不等式可化为
(x+1)(3x-4) >0,
解得 x<-1或 x> 43?,
故原不等式的解集为
{ x∣ x<-1或 x> 43}.
?
(5) 2x2+4x+3>0;
解:该不等式可化为
2(x+1)2+1>0,
恒成立,
故原不等式的解集为R.
(6) 9x2-6x+1≤0.
解:该不等式可化为(3x-1)2 ≤0,
解得 x=13,
故原不等式的解集为{ x∣x=13 }.
?
3. 解下列不等式:
(1) -6x2-x+2<0;
解:不等式可变形为
6x2+x-2>0 ,
对应方程的两根分别为12和-23,
由 y=6x2+x-2的图象知解集为
{ x∣x <-23 或 x>12 }
?
(2) 1-4x2≥4x+2;
解:不等式可变形为4x2+4x+1<0,
即(2x+1)2<0,
显然无解,
即解集为?.
(3) 1-3x<x2;
解:不等式可变形为
x2+3x-1>0,
对应方程的两根为
x1,2=-3±9+42= -3±132,
由 y=x2+3x-1的图象知解集为
{ x∣x < -3-132 或 x > -3+132 }.
?
(4) (x-2)(x+2) >1.
解:不等式可变形为 x2-5>0,
对应方程的两根为
x1=-5,x2=5,
由 y=x2-5 的图象知解集为
{ x∣x<-5 或 x>5 }.
?
4. 当 x 是什么实数时,函数 y=-x2+5x+14 的值是:
(1) 0?
解: -x2+5x+14=0
x2-5x-14=0
(x-7)(x+2) =0
x1=7,x2=-2
(2) 正数?
解: -x2+5x+14>0
x2-5x-14<0
(x-7)(x+2) <0
-2<x<7
(3) 负数?
解: -x2+5x+14<0
x2-5x-14>0
(x-7)(x+2) >0
x>7 或 x<-2.
5. (1)已知集合 M={x|-4≤x≤7,N={x|x2-x-6>0}, 求M∩N;
解:∵集合M = {x∣-4≤x≤7},
N = {x|x2-x-6>0}
= {x∣x<-2或 x>3},
∴ M∩N ={x∣-4≤x<-2 或 3< x≤7};
(2) 已知集合 A={x|x2-4x+3<0},B={x|(x-2)(x-5) <0},求 A∪B.
解:∵集合A={x|x2-4x+3<0}
={x∣1<x<3},
B={x|(x-2)(x-5)<0}
={x∣2<x<5},
∴ A∪B ={x∣1<x<5}.
错因分析
易错点 随意消项致错
A
一、选择题
1.不等式6x2+x-2≤0的解集为( )
解析 因为6x2+x-2≤0?(2x-1)(3x+2)≤0,
分层练习-基础
D
3.如果关于x的不等式x2
解析 不等式x2
故1和3是x2-ax-b=0的两根,
解得a=4,b=-3.
所以ba=(-3)4=81.故选B.
B
4.在R上定义运算“⊙”:a⊙b=ab+2a+b,则满足x⊙(x-2)<0的实数x的取值范围为( )
A.{x|0
x⊙(x-2)=x(x-2)+2x+(x-2)=x2+x-2=(x+2)(x-1),
又x⊙(x-2)<0,
则(x+2)(x-1)<0,
故不等式的解集是{x|-2
5.若一元二次不等式ax2+bx+c<0的解集为{x|x<-3或x>5},则ax2-bx+c<0的解集为( )
A.{x|x<-5或x>3} B.{x|-5
由根与系数的关系得:
代入得ax2+2ax-15a<0,
又由解集的形式知a<0,∴x2+2x-15>0,
∴(x-3)(x+5)>0
∴x>3或x<-5.
4
故a+b=4.
7.不等式-1
{x|-3≤x<-2或0
ax2+bx+c≥0的解集为_______________.
[-1,2]
解析 由题意ax2+bx+c=a(x-2)(x+1),
故原不等式可化为a(x-2)(x+1)≥0,
又∵a<0,∴(x-2)(x+1)≤0,
所求解集为[-1,2].
三、解答题
9.解下列不等式:
(1)2x2+5x-3<0;(2)-3x2+6x≤2;
(2)原不等式等价于3x2-6x+2≥0.
(3)4x2-4x+1>0;(4)-x2+6x-10>0.
作出函数y=4x2-4x+1的图象如图③.
③
(4)原不等式可化为x2-6x+10<0,
∵Δ=36-40=-4<0,
∴方程x2-6x+10=0无实根,
∴原不等式的解集为?.
10.已知不等式x2+x-6<0的解集为A,不等式x2-2x-3<0的解集为B.
(1)求A∩B;
(2)若不等式x2+ax+b<0的解集为A∩B,求不等式ax2+bx+3<0的解集.
解 (1)由x2+x-6<0得-3
∴不等式ax2+bx+3<0为-x2-2x+3<0,即x2+2x-3>0,
解得x<-3或x>1.
∴所求不等式的解集为{x|x<-3或x>1}.
BC
11.(多选题)下列不等式的解集为R的是( )
B中,Δ=62-4×10<0,解集为R;
C中,不等式可化为x2-x+2>0,Δ=(-1)2-4×2<0,解集为R;
D中不等式化为2x2-3x+3<0,Δ=(-3)2+4×2×3<0,解集为?.
分层练习-巩固
∴m的取值范围是{m|m<0}.
(-∞,0)
13.解关于x的不等式x2-(a+a2)x+a3>0(a∈R).
解 原不等式可化为(x-a)(x-a2)>0.
当a<0时,a
当a=0时,a2=a,原不等式的解集为{x|x≠0,x∈R};
当0
当a=1时,a2=a,原不等式的解集为{x|x≠1,x∈R};
当a>1时,a
综上所述,当a<0或a>1时,原不等式的解集为{x|x
当0
当a=1时,原不等式的解集为{x|x≠1,x∈R};
当a=0时,原不等式的解集为{x|x≠0,x∈R}.
又f(1)=a-b+c>0,f(-1)=a+b+c<0,
作出函数y=ax2-bx+c的简图如图.
③⑤
∴b<0,而f(0)=c>0,
故③⑤正确.
分层练习-拓展
1.掌握1个知识点——一元二次不等式的解法
(1)图象法:由一元二次方程、一元二次不等式及二次函数的关系,可以得到解一元二次不等式的一般步骤:
①化不等式为标准形式:ax2+bx+c>0(a>0)或ax2+bx+c<0(a>0);
②求方程ax2+bx+c=0(a>0)的根,并画出对应函数y=ax2+bx+c图象的简图;
③由图象得出不等式的解集.
(2)代数法:将所给不等式化为一般式后借助分解因式或配方求解.
当m<n时,若(x-m)(x-n)>0,则可得{x|x>n或x<m};若(x-m)(x-n)<0,则可得{x|m<x<n}.
有口诀如下:大于取两边,小于取中间.
课堂小结
2.突破1个重难点——含参数的一元二次不等式的解法
在解含参数的一元二次型的不等式时,往往要对参数进行分类讨论,为了做到分类“不重不漏”,讨论需从如下三个方面进行考虑
(1)关于不等式类型的讨论:二次项系数a>0,a<0,a=0.
(2)关于不等式对应的方程根的讨论:两根(Δ>0),一根(Δ=0),无根(Δ<0).
(3)关于不等式对应的方程根的大小的讨论:x1>x2,x1=x2,x1<x2.
3.规避1个易误点
当二次项系数小于0时,需两边同乘-1,化为正的.
课堂小结
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
