4.1.2 指数幂的拓展 课件(共49张PPT)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一)
文档属性
| 名称 | 4.1.2 指数幂的拓展 课件(共49张PPT)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 10:19:44 | ||
图片预览







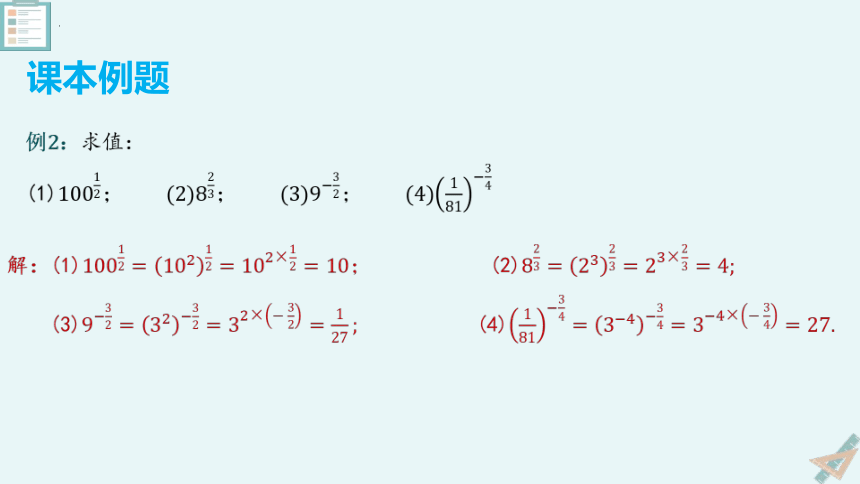


文档简介
(共49张PPT)
苏教版2019高一数学(必修一)第四章 指数与对数
4.1.2 指数幂的拓展
4.1 指 数
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
观察下面的变形:
(25)2 = 210 ,
得 = 25.
又由 5 = ,得
=.
类似地,可以得到 = ,
= ,
······
情景导入
这表明,当 m 被 n 整除时,就有
( a>0,m,n 均为正整数 ).
一般地,我们规定
= ( a>0,m,n 均为正整数 ).
新知探究
这就是正数 a 的正分数指数幂的意义.
由此可知, 的意义为
= .
仿照负整数指数幂的意义,我们规定
( a>0,m,n 均为正整数 ).
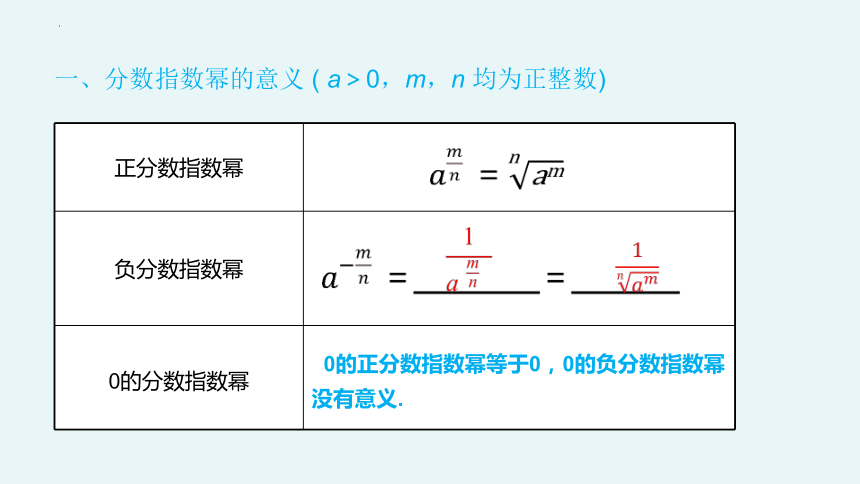
一、分数指数幂的意义 ( a>0,m,n 均为正整数)
正分数指数幂
负分数指数幂
0的分数指数幂 0的正分数指数幂等于0,0的负分数指数幂没有意义.
=
=_______=______
二、有理数指数幂的运算性质
asat =as+t,
(as)t =ast,
(ab)t =atbt,
其中 s,t∈Q,a>0,b>0.
例2:求值:
(1)
解:(1) (2)
(3) (4)
课本例题
例3:用分数指数幂的形式表示并计算下列各式(其中)
(1)
解:(1) (2)
(3)
课本例题
我们已将指数式 ax中的指数 从整数推广到分数 (有理数),是否还可以将指数推广到无理数呢
例如,“”有意义吗
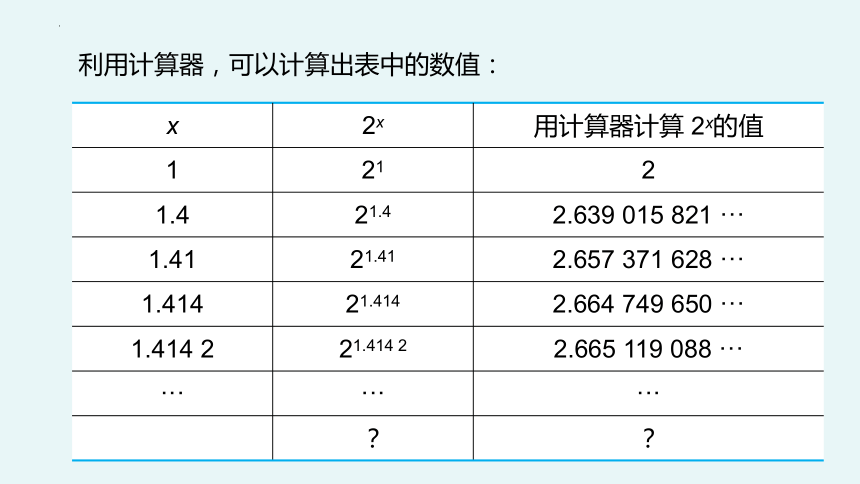
利用计算器,可以计算出表中的数值:
x 2x 用计算器计算 2x的值
1 21 2
1.4 21.4 2.639 015 821 ···
1.41 21.41 2.657 371 628 ···
1.414 21.414 2.664 749 650 ···
1.414 2 21.414 2 2.665 119 088 ···
··· ··· ···
? ?
随着 x 的取值越来越接近于,2x 的值也越来越接近于一个实数,我们把这个实数记为
一般地,当 a>0 且x是一个无理数时,ax也是一个确定的实数有理数指数幂的运算性质对无理数指数幂同样适用.
这样,指数幂的概念从有理指数幂推广到实数指数幂.
以后可以证明,当a>0,a≠1,N>0时,一定有唯一的实数 x ,满足 ax=N.
1. 用根式的形式表示下列各式 (a>0):
=
=
=
= =a
课本练习
2. 用分数指数幂表示下列各式:
(1) (a>0);
(2) ;
(4) (x>0);
= (a>0)
=
= (x>0)
(5)(y>0);
(6) (m>0);
(7) ;
(8) (m>n).
= (y>0)
= (m>0)
=
=m-n,(m>n)
3. 求下列各式的值:
(1) ;
(2) ;
(3) ;
(4) ;
=
=
=
=
(5) 2××.
4. 化简下列各式 ( a>0,b>0,x>0,y>0):
∵ a>0,
∴ 原式= =
∵ a>0,
∴ 原式= =
∵ a>0,
∴ 原式= =
∵ a>0,
∴ 原式=
∵ a>0,
∴ 原式=
∵ x>0,y>0,
∴ 原式=
∵ a>0,b>0,
∴ 原式=
∵ x>0,y>0,
∴ 原式= x3y2÷x =x2
D
分层练习-基础
B
A
C
=a2·a2=a4.
A.a16 B.a8 C.a4 D.a2
BD
5.(多选题)下列各式中一定成立的有( )
C中当x=y=1时,等式不成立;D正确.故选BD.
二、填空题
6.已知3a=2,3b=5,则32a-b=________.
三、解答题
9.求下列各式的值:
解析 因为m=2,n=3,
所以原式=
分层练习-巩固
3
13.(1)已知2x+2-x=a(常数),求16x+16-x的值;
解 ∵4x+4-x=(2x)2+(2-x)2=(2x+2-x)2-2·2x·2-x=a2-2,
∴(4x+4-x)2=16x+16-x+2=(a2-2)2=a4-4a2+4,
∴16x+16-x=a4-4a2+2.
∵x+y=12,xy=9,②
∴(x-y)2=(x+y)2-4xy=122-4×9=108.
a,b,c均为正整数,∴abc=70=2×5×7,
又a,b,c为正整数且a≤b≤c,∴a=2,b=5,c=7.
解 ∵ax=70w且x,w为非零实数,
分层练习-拓展
感受·理解
1. 求下列各式的值:
(1) ; (2) ;
(3) ; (4) ;
(5) (x>y); (6) .
==4
==
= 102-100
= -0.1
=∣x-y∣ = x-y
=-(2x+y) =-2x-y
习题4.1
2. 用分数指数幂表示下列各式(a>0,b>0);
(1) ; (2) ;
(3) a ; (4) ()2;
(5) · ; (6) ;
(7) ·; (8) ()2 ·.
=a
=a
=a
=a
=a
=a
=a
=a b
3. 求下列各式的值:
(1) 36 ;
(2) () ;
(3) 10 000 ;
(4) () ;
(5) 4 ;
-
(6) (6) ;
==6
=
=10
=
=
=
4. 用计算器计算下列各式的值:
(1) 5 ;
(2) 321 ;
(3) 25.8 ;
(4) 723 ;
= ≈1.709 976
= ≈46.881 700
= ≈11.447 609
= ≈58 241.224 3
5. 化简下列各式(a>0,b>0):
(1) a a a ;
(2) a a ÷a ;
(3) ( a a )12;
(4) ( a b )12;
-
(5) 4a b ÷ (-a b );
-
-
-
(6) 2a ( a -2a );
-
-
(7) (2a +3b )(2a -3b );
-
-
(8) (a2-2+a-2) ÷(a2-a-2).
6. 设a,b是正数,下列各题中的两个代数式是否恒等
为什么
(am)n与aman;
(2) a 与;
(3) a 与;
(4) (a+b)n 与 an+bn.
思考·运用
7. 利用分数指数幂计算:(-)(++).
8. 已知 a+a-1=3,求下列各式的值:
(1) a -a ;
-
(2) a -a ;
-
x3-y3=(x-y) (x2+xy+y2),
x3+y3= (x+y)(x2-xy+y2).
9. 解下列方程:
(1) x =;
-
(2) 2x -1 =15;
1.掌握2个知识点
(1)分数指数幂的意义;(2)分数指数幂的运算性质.
2.掌握2种方法
(1)对根式进行运算时,一般先将根式化成分数指数幂,这样可以方便使用同底数幂的运算律.
(2)解决较复杂的条件求值问题时,“整体思想”是简化求解的“利器”.
3.规避1个易错点
在运用分数指数幂的运算性质化简时,其结果不能同时含有根式和分数指数,也不能既含有分母又含有负指数.
课堂小结
苏教版2019高一数学(必修一)第四章 指数与对数
4.1.2 指数幂的拓展
4.1 指 数
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
观察下面的变形:
(25)2 = 210 ,
得 = 25.
又由 5 = ,得
=.
类似地,可以得到 = ,
= ,
······
情景导入
这表明,当 m 被 n 整除时,就有
( a>0,m,n 均为正整数 ).
一般地,我们规定
= ( a>0,m,n 均为正整数 ).
新知探究
这就是正数 a 的正分数指数幂的意义.
由此可知, 的意义为
= .
仿照负整数指数幂的意义,我们规定
( a>0,m,n 均为正整数 ).
一、分数指数幂的意义 ( a>0,m,n 均为正整数)
正分数指数幂
负分数指数幂
0的分数指数幂 0的正分数指数幂等于0,0的负分数指数幂没有意义.
=
=_______=______
二、有理数指数幂的运算性质
asat =as+t,
(as)t =ast,
(ab)t =atbt,
其中 s,t∈Q,a>0,b>0.
例2:求值:
(1)
解:(1) (2)
(3) (4)
课本例题
例3:用分数指数幂的形式表示并计算下列各式(其中)
(1)
解:(1) (2)
(3)
课本例题
我们已将指数式 ax中的指数 从整数推广到分数 (有理数),是否还可以将指数推广到无理数呢
例如,“”有意义吗
利用计算器,可以计算出表中的数值:
x 2x 用计算器计算 2x的值
1 21 2
1.4 21.4 2.639 015 821 ···
1.41 21.41 2.657 371 628 ···
1.414 21.414 2.664 749 650 ···
1.414 2 21.414 2 2.665 119 088 ···
··· ··· ···
? ?
随着 x 的取值越来越接近于,2x 的值也越来越接近于一个实数,我们把这个实数记为
一般地,当 a>0 且x是一个无理数时,ax也是一个确定的实数有理数指数幂的运算性质对无理数指数幂同样适用.
这样,指数幂的概念从有理指数幂推广到实数指数幂.
以后可以证明,当a>0,a≠1,N>0时,一定有唯一的实数 x ,满足 ax=N.
1. 用根式的形式表示下列各式 (a>0):
=
=
=
= =a
课本练习
2. 用分数指数幂表示下列各式:
(1) (a>0);
(2) ;
(4) (x>0);
= (a>0)
=
= (x>0)
(5)(y>0);
(6) (m>0);
(7) ;
(8) (m>n).
= (y>0)
= (m>0)
=
=m-n,(m>n)
3. 求下列各式的值:
(1) ;
(2) ;
(3) ;
(4) ;
=
=
=
=
(5) 2××.
4. 化简下列各式 ( a>0,b>0,x>0,y>0):
∵ a>0,
∴ 原式= =
∵ a>0,
∴ 原式= =
∵ a>0,
∴ 原式= =
∵ a>0,
∴ 原式=
∵ a>0,
∴ 原式=
∵ x>0,y>0,
∴ 原式=
∵ a>0,b>0,
∴ 原式=
∵ x>0,y>0,
∴ 原式= x3y2÷x =x2
D
分层练习-基础
B
A
C
=a2·a2=a4.
A.a16 B.a8 C.a4 D.a2
BD
5.(多选题)下列各式中一定成立的有( )
C中当x=y=1时,等式不成立;D正确.故选BD.
二、填空题
6.已知3a=2,3b=5,则32a-b=________.
三、解答题
9.求下列各式的值:
解析 因为m=2,n=3,
所以原式=
分层练习-巩固
3
13.(1)已知2x+2-x=a(常数),求16x+16-x的值;
解 ∵4x+4-x=(2x)2+(2-x)2=(2x+2-x)2-2·2x·2-x=a2-2,
∴(4x+4-x)2=16x+16-x+2=(a2-2)2=a4-4a2+4,
∴16x+16-x=a4-4a2+2.
∵x+y=12,xy=9,②
∴(x-y)2=(x+y)2-4xy=122-4×9=108.
a,b,c均为正整数,∴abc=70=2×5×7,
又a,b,c为正整数且a≤b≤c,∴a=2,b=5,c=7.
解 ∵ax=70w且x,w为非零实数,
分层练习-拓展
感受·理解
1. 求下列各式的值:
(1) ; (2) ;
(3) ; (4) ;
(5) (x>y); (6) .
==4
==
= 102-100
= -0.1
=∣x-y∣ = x-y
=-(2x+y) =-2x-y
习题4.1
2. 用分数指数幂表示下列各式(a>0,b>0);
(1) ; (2) ;
(3) a ; (4) ()2;
(5) · ; (6) ;
(7) ·; (8) ()2 ·.
=a
=a
=a
=a
=a
=a
=a
=a b
3. 求下列各式的值:
(1) 36 ;
(2) () ;
(3) 10 000 ;
(4) () ;
(5) 4 ;
-
(6) (6) ;
==6
=
=10
=
=
=
4. 用计算器计算下列各式的值:
(1) 5 ;
(2) 321 ;
(3) 25.8 ;
(4) 723 ;
= ≈1.709 976
= ≈46.881 700
= ≈11.447 609
= ≈58 241.224 3
5. 化简下列各式(a>0,b>0):
(1) a a a ;
(2) a a ÷a ;
(3) ( a a )12;
(4) ( a b )12;
-
(5) 4a b ÷ (-a b );
-
-
-
(6) 2a ( a -2a );
-
-
(7) (2a +3b )(2a -3b );
-
-
(8) (a2-2+a-2) ÷(a2-a-2).
6. 设a,b是正数,下列各题中的两个代数式是否恒等
为什么
(am)n与aman;
(2) a 与;
(3) a 与;
(4) (a+b)n 与 an+bn.
思考·运用
7. 利用分数指数幂计算:(-)(++).
8. 已知 a+a-1=3,求下列各式的值:
(1) a -a ;
-
(2) a -a ;
-
x3-y3=(x-y) (x2+xy+y2),
x3+y3= (x+y)(x2-xy+y2).
9. 解下列方程:
(1) x =;
-
(2) 2x -1 =15;
1.掌握2个知识点
(1)分数指数幂的意义;(2)分数指数幂的运算性质.
2.掌握2种方法
(1)对根式进行运算时,一般先将根式化成分数指数幂,这样可以方便使用同底数幂的运算律.
(2)解决较复杂的条件求值问题时,“整体思想”是简化求解的“利器”.
3.规避1个易错点
在运用分数指数幂的运算性质化简时,其结果不能同时含有根式和分数指数,也不能既含有分母又含有负指数.
课堂小结
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
