4.2.1 对数的概念 课件(共32张PPT)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一)
文档属性
| 名称 | 4.2.1 对数的概念 课件(共32张PPT)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 10:20:18 | ||
图片预览











文档简介
(共32张PPT)
苏教版2019高一数学(必修一)第四章 指数与对数
4.2 对 数
4.2.1 对数的概念
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
1.理解对数的概念.
2.知道自然对数和常用对数.
3.会用对数的定义进行对数式与指数式的互化.
4.通过理解和掌握对数的性质,求简单的对数值,发展数学抽象及数学运算素养.
已知1个细胞经过 x 次分裂后,相应的细胞个数为
y=2x.
由此,若知道了分裂的次数 x,就能求出分裂后相应的细胞数 y . 反过来,
● 若知道了分裂后相应的细胞数 y,怎样求出分裂的次数 x 呢
情景导入
一、对数的概念
(1) 定义:
一般地,如果 ab=N (a>0,a≠1),那么就称 b 是以 a 为底 N 的对数,记作__________,其中,a叫作对数的底数,N叫作真数.
logaN=b
上述问题也就是在 y=2x中,已知 y,求 x 此时问题就转化为已知底数和幂的值求指数的问题.
新知探究
(2) 特殊对数:
常用对数:以10为底,记作________;
自然对数:以e为底,记作_________.
(3) 指数与对数的关系:
当 a>0,a≠1 时,ab=N __________.
lg N
ln N
b=logaN
由对数的定义可知,ab=N与 b= logaN 两个等式所表示的是a,b,N 这3个量之间的同一个关系.
例如:
32 = 9 log39=2,
log42 = 4 =2.
根据对数的定义,要解决本节开头提出的问题,就只要计算 log2y 的值.
例 1
将下列指数式改写成对数式:
(1) 24 = 16; (2) 3-3 =;
(3) 5a = 20; (4) ()b=0.45.
解:log216 = 4.
解:log3 =-3.
解:log220 = 5.
解:log3 0.45=b.
课本例题
例 2
将下列对数式改写成指数式:
(1) log5125=3;
(2) log 3=-2;
(3) log10 a =-1.699.
解:53 = 125.
解:()-2= 3.
解:10-1.699 = a .
课本例题
例 3
求下列各式的值:
(1) log264;
解:由 26=64 ,得 log264 = 6.
课本例题
(2) log9 27.
解:设 x=log927,则根据对数的定义知 9x=27,
即 32x=33,
得 2x=3,x=,
所以 log927= .
二、常用对数
通常将以10为底的对数称为常用对数 ,如log102,log1012 等.为了方便起见,对数 log10N 简记为lg N,如 lg 2,lg 12 等.
三、自然对数
在科学技术中,常常使用以 e为底的对数,这种对数称为自然对数. e=2.718 28···是一个无理数. 正数N的自然对数 logeN 一般简记为 ln N,如loge2,loge15 分别记为 ln 2,ln 15 等.
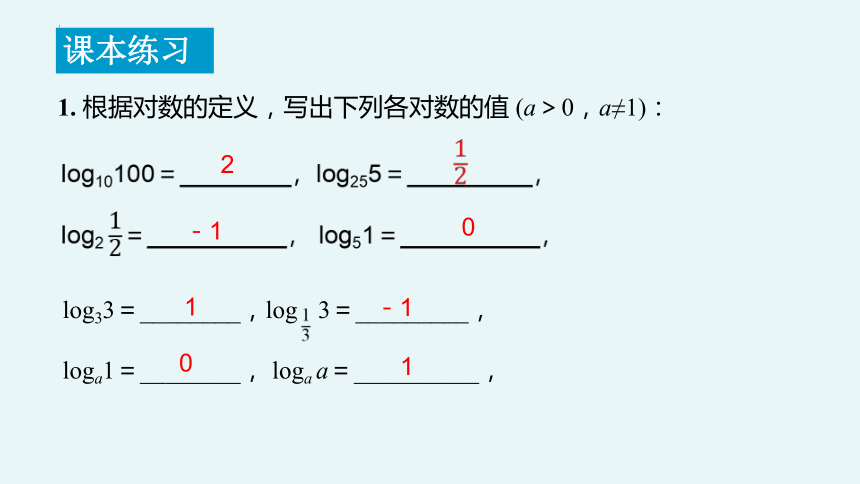
1. 根据对数的定义,写出下列各对数的值 (a>0,a≠1):
log10100=________,log255=_________,
log2 =__________, log51=__________,
2
-1
0
课本练习
log33=________,log 3=_________,
loga1=________, loga a=__________,
1
-1
0
1
2. 填空:
题 号 指 数 式 对 数 式
(1) 24=16 log216=4
(2)
(3) 5a=25 log525=a
3. 将下列指数式改写成对数式:
(1) 35=243; (2) 2-8=;
(3) 2x=10; (4) ()x=12.
log3243=5
log2 =-8
log210=x
log 12=x
4. 将下列对数式改写成指数式:
(1) log 4 = - 4; (2) lg 10 000=4;
(3) lg a= 0.4771; (4) ln 12=b.
()-4 =4
104=10000
100.4771=a
eb=12
5. 求下列各式的值:
(1) log4 64; (2) log7 ;
(3) log2 ; (4) log 9;
(5) 1g 1000; (6) ln .
=3
=
=-3
=-2
=3
=-2
6. 利用计算器计算下列对数的值(结果保留4 位小数):
(1) lg 2; (2) lg 5;
(3) lg 1.078; (4) lg 0.84.
≈0.3010
≈0.6990
≈0.0326
≈-0.0757
7. 已知 a>0,a≠1,N>0,b∈R.
(1) logaa2 =_____________,logaa5 =___________,
logaa-3=____________,logaa =___________,
一般地,logaab=__________,请证明这个结论;
2log2a
5
-3
b
(2) 证明: a = N.
logaN
C
一、选择题
1.如果a=b2(b>0,b≠1),则有( )
A.log2a=b B.log2b=a
C.logba=2 D.logb2=a
解析 指数式b2=a化为对数式2=logba.
分层练习-基础
B
3.设a=log310,b=log37,则3a-b的值为( )
A
解析 因为log2x=3,所以x=23=8.
D
AD
5.(多选题)下列结论正确的是( )
A.lg(lg10)=0
B.若10=lg x,则x=10
C.若e=ln x,则x=e2
D.使log(x-1)(x+2)有意义的x的取值范围是(1,2)∪(2,+∞)
解析 lg(lg 10)=lg 1=0,故A正确;
若10=lg x,则x=1010,故B错误;
若e=ln x,则x=ee,故C错误;
8
7.若log2(log3x)=log3(log4y)=0,则x=________,y=________.
解析 ∵log2(log3x)=0,∴log3x=1,∴x=3.
∵log3(log4y)=0,∴log4y=1,∴y=4.
3
4
解析 ∵3log2x=3-3,
三、解答题
9.将下列指数式、对数式互化.
解 (1)log3243=5;
(4)27=128.
10.求下列各式中的x的值.
解 (4)由log5(log2x)=0,得log2x=1.
∴x=2.
ACD
11.(多选题)下列指数式与对数式互化正确的有( )
解析 log39=2化为指数式为32=9,故B错误;A,C,D正确.
分层练习-巩固
3
13.求下列各式中的x的值.
解 (1)∵log5(log2x)=1,
∴log2x=5,∴x=25=32.
∵310>215>56,∴y>x>z.
分层练习-拓展
1.理解4个知识点
(1)对数的概念. (2)自然对数、常用对数.
(3)指数式与对数式的互化. (4)对数的性质.
课堂小结
2.理清1组关系——指数式与对数式的关系
(1)对数概念与指数概念有关,指数式和对数式是互逆的,即ab=N logaN=b(a>0,且a≠1,N>0),据此可得两个常用恒等式:①logaab=b;②alogaN=N.
(2)在关系式ax=N中,已知a和x求N的运算称为求幂运算,而如果已知a和N求x的运算就是对数运算,两个式子实质相同而形式不同,互为逆运算.
3.规避1个易错点
注意对数式中底数与真数的范围.
课堂小结
苏教版2019高一数学(必修一)第四章 指数与对数
4.2 对 数
4.2.1 对数的概念
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
1.理解对数的概念.
2.知道自然对数和常用对数.
3.会用对数的定义进行对数式与指数式的互化.
4.通过理解和掌握对数的性质,求简单的对数值,发展数学抽象及数学运算素养.
已知1个细胞经过 x 次分裂后,相应的细胞个数为
y=2x.
由此,若知道了分裂的次数 x,就能求出分裂后相应的细胞数 y . 反过来,
● 若知道了分裂后相应的细胞数 y,怎样求出分裂的次数 x 呢
情景导入
一、对数的概念
(1) 定义:
一般地,如果 ab=N (a>0,a≠1),那么就称 b 是以 a 为底 N 的对数,记作__________,其中,a叫作对数的底数,N叫作真数.
logaN=b
上述问题也就是在 y=2x中,已知 y,求 x 此时问题就转化为已知底数和幂的值求指数的问题.
新知探究
(2) 特殊对数:
常用对数:以10为底,记作________;
自然对数:以e为底,记作_________.
(3) 指数与对数的关系:
当 a>0,a≠1 时,ab=N __________.
lg N
ln N
b=logaN
由对数的定义可知,ab=N与 b= logaN 两个等式所表示的是a,b,N 这3个量之间的同一个关系.
例如:
32 = 9 log39=2,
log42 = 4 =2.
根据对数的定义,要解决本节开头提出的问题,就只要计算 log2y 的值.
例 1
将下列指数式改写成对数式:
(1) 24 = 16; (2) 3-3 =;
(3) 5a = 20; (4) ()b=0.45.
解:log216 = 4.
解:log3 =-3.
解:log220 = 5.
解:log3 0.45=b.
课本例题
例 2
将下列对数式改写成指数式:
(1) log5125=3;
(2) log 3=-2;
(3) log10 a =-1.699.
解:53 = 125.
解:()-2= 3.
解:10-1.699 = a .
课本例题
例 3
求下列各式的值:
(1) log264;
解:由 26=64 ,得 log264 = 6.
课本例题
(2) log9 27.
解:设 x=log927,则根据对数的定义知 9x=27,
即 32x=33,
得 2x=3,x=,
所以 log927= .
二、常用对数
通常将以10为底的对数称为常用对数 ,如log102,log1012 等.为了方便起见,对数 log10N 简记为lg N,如 lg 2,lg 12 等.
三、自然对数
在科学技术中,常常使用以 e为底的对数,这种对数称为自然对数. e=2.718 28···是一个无理数. 正数N的自然对数 logeN 一般简记为 ln N,如loge2,loge15 分别记为 ln 2,ln 15 等.
1. 根据对数的定义,写出下列各对数的值 (a>0,a≠1):
log10100=________,log255=_________,
log2 =__________, log51=__________,
2
-1
0
课本练习
log33=________,log 3=_________,
loga1=________, loga a=__________,
1
-1
0
1
2. 填空:
题 号 指 数 式 对 数 式
(1) 24=16 log216=4
(2)
(3) 5a=25 log525=a
3. 将下列指数式改写成对数式:
(1) 35=243; (2) 2-8=;
(3) 2x=10; (4) ()x=12.
log3243=5
log2 =-8
log210=x
log 12=x
4. 将下列对数式改写成指数式:
(1) log 4 = - 4; (2) lg 10 000=4;
(3) lg a= 0.4771; (4) ln 12=b.
()-4 =4
104=10000
100.4771=a
eb=12
5. 求下列各式的值:
(1) log4 64; (2) log7 ;
(3) log2 ; (4) log 9;
(5) 1g 1000; (6) ln .
=3
=
=-3
=-2
=3
=-2
6. 利用计算器计算下列对数的值(结果保留4 位小数):
(1) lg 2; (2) lg 5;
(3) lg 1.078; (4) lg 0.84.
≈0.3010
≈0.6990
≈0.0326
≈-0.0757
7. 已知 a>0,a≠1,N>0,b∈R.
(1) logaa2 =_____________,logaa5 =___________,
logaa-3=____________,logaa =___________,
一般地,logaab=__________,请证明这个结论;
2log2a
5
-3
b
(2) 证明: a = N.
logaN
C
一、选择题
1.如果a=b2(b>0,b≠1),则有( )
A.log2a=b B.log2b=a
C.logba=2 D.logb2=a
解析 指数式b2=a化为对数式2=logba.
分层练习-基础
B
3.设a=log310,b=log37,则3a-b的值为( )
A
解析 因为log2x=3,所以x=23=8.
D
AD
5.(多选题)下列结论正确的是( )
A.lg(lg10)=0
B.若10=lg x,则x=10
C.若e=ln x,则x=e2
D.使log(x-1)(x+2)有意义的x的取值范围是(1,2)∪(2,+∞)
解析 lg(lg 10)=lg 1=0,故A正确;
若10=lg x,则x=1010,故B错误;
若e=ln x,则x=ee,故C错误;
8
7.若log2(log3x)=log3(log4y)=0,则x=________,y=________.
解析 ∵log2(log3x)=0,∴log3x=1,∴x=3.
∵log3(log4y)=0,∴log4y=1,∴y=4.
3
4
解析 ∵3log2x=3-3,
三、解答题
9.将下列指数式、对数式互化.
解 (1)log3243=5;
(4)27=128.
10.求下列各式中的x的值.
解 (4)由log5(log2x)=0,得log2x=1.
∴x=2.
ACD
11.(多选题)下列指数式与对数式互化正确的有( )
解析 log39=2化为指数式为32=9,故B错误;A,C,D正确.
分层练习-巩固
3
13.求下列各式中的x的值.
解 (1)∵log5(log2x)=1,
∴log2x=5,∴x=25=32.
∵310>215>56,∴y>x>z.
分层练习-拓展
1.理解4个知识点
(1)对数的概念. (2)自然对数、常用对数.
(3)指数式与对数式的互化. (4)对数的性质.
课堂小结
2.理清1组关系——指数式与对数式的关系
(1)对数概念与指数概念有关,指数式和对数式是互逆的,即ab=N logaN=b(a>0,且a≠1,N>0),据此可得两个常用恒等式:①logaab=b;②alogaN=N.
(2)在关系式ax=N中,已知a和x求N的运算称为求幂运算,而如果已知a和N求x的运算就是对数运算,两个式子实质相同而形式不同,互为逆运算.
3.规避1个易错点
注意对数式中底数与真数的范围.
课堂小结
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
