4.2.2 等差数列的前n项和(第2课时)(同步课件(共24张PPT)-高二数学同步精品课堂(人教A版2019选择性必修第二册)
文档属性
| 名称 | 4.2.2 等差数列的前n项和(第2课时)(同步课件(共24张PPT)-高二数学同步精品课堂(人教A版2019选择性必修第二册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览








文档简介
人教A版选择性必修第二册
第四章 数列
4.2 等差数列
4.2.2 等差数列的前n项和公式(第2课时)
学习目标
1
2
3
理解等差数列的通项公式与前n 项和公式的关系
?
理解并能应用等差数列前n 项和的性质,培育逻辑推理、数学运算的核心素养;
?
能较熟练应用等差数列前n项和公式求和
复习回顾
2.在上一节中我们学习过了等差数列的哪些性质?
1.等差数列的前n项和公式:
“知三求二”
性质1 若{an}是等差数列,公差为d,则ak,ak+m,ak+2m,…(k,m∈N*)是公差为md的等差数列.
性质2 在等差数列{an}中,若m+n=p+q(m,n,p,q∈N*),则am+an=ap+aq.
性质3 数列{an}, {bn}都是等差数列, 公差分别为d1, d2,则数{pan+qbn}(p,q为常数)是公差为pd1+qd2的等差数列.
那么,结合等差数列的前n项和公式,等差数列还会哪些性质?
新课讲授
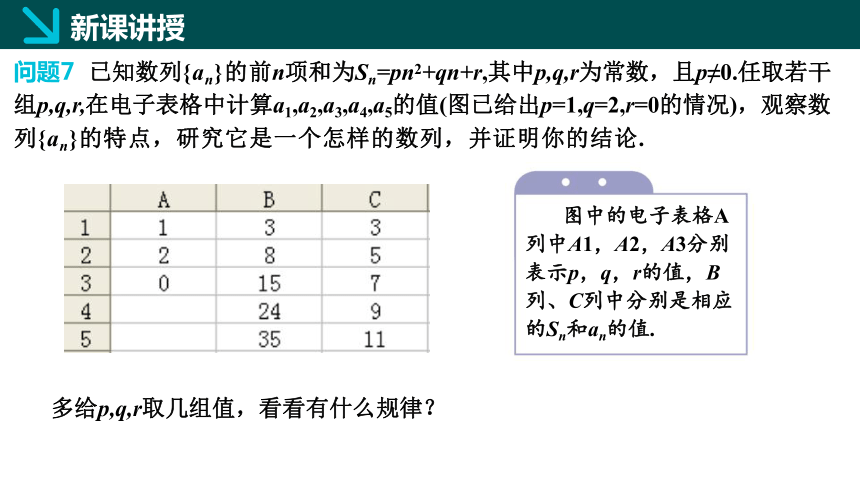
问题7 已知数列{an}的前n项和为Sn=pn2+qn+r,其中p,q,r为常数,且p≠0.任取若干组p,q,r,在电子表格中计算a1,a2,a3,a4,a5的值(图已给出p=1,q=2,r=0的情况),观察数列{an}的特点,研究它是一个怎样的数列,并证明你的结论.
图中的电子表格A列中A1,A2,A3分别表示p,q,r的值,B列、C列中分别是相应的Sn和an的值.
多给p,q,r取几组值,看看有什么规律?
新课讲授
证明:
结论:若数列{an}的前n项和是一个不含有常数项的二次函数,则该数列是等差数列.
性质4 数列{an}是等差数列?Sn=An2+Bn (A,B为常数).
?
学以致用
教材P24
[例2] 已知一个等差数列{an}前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗?
例题再现
思考 对于上节课的这道例题中的等差数列,还有其他解法求Sn吗?
解法1:
变式 已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
3. 在等差数列{an}中,Sn为其前n项的和,若S4=6,S8=20,求S16 .
学以致用
教材P23
利用性质4还可以怎样解?
新知探究
证明:
教材P25
性质5
典例分析
变式 已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
思考 利用性质5还可以怎样解?
解法2:
新知探究
问题1
证明:
性质6
典例分析
变式 已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
思考 利用性质6还可以怎样解?
解法3:
学以致用
教材P23
5. 已知一个等差数列的项数为奇数,其中所有奇数项的和为290,所有偶数项的和为261. 求此数列中间一项的值以及项数.
问题2 通过解决本题,等差数列又会有什么性质呢?这个性质和什么有关呢?
如果一个等差数列的项数为偶数,又会怎样呢?
新知探究
问题2 通过解决本题,等差数列又会有什么性质呢?这个性质和什么有关呢?
(1)若一个等差数列的项数为奇数,设其项数为2n+1,则
最中间一项
性质7
新知探究
问题2 通过解决本题,等差数列又会有什么性质呢?这个性质和什么有关呢?
(2)若一个等差数列的项数为偶数,设其项数为2n,则
性质8
新知探究
问题3 如果数列{an}、{bn}是项数相同的等差数列,Sn、Tn分别是它们前n项和,那么S2n-1与T2n-1会有什么关系?
性质9
能力提升
题型一
利用数列的前???? 项和判断等差数列
?
例题
1.已知数列{????????}的前????项和????????=????????+???? .
?
(1)求数列{????????} 的通项公式;
?
(2)判断{????????} 是不是等差数列,并说明理由.
?
[解析] (1)当n=1时,a1=S1=12+1=2 ;
当n≥2时,an=Sn?Sn?1=n2+1?n?12?1=2n?1 ,
又a1=2不满足上式,∴an=&2,n=1,&2n?1,n≥2.
?
(2)解法一:∵a1=2,a2=3,a3=5,a2?a1≠a3?a2 ,
∴{an} 不是等差数列.
解法二:∵ 等差数列的前n项和Sn=na1+nn?12d=d2n2+a1?d2n ,
当d2≠0时,其是不含常数项的二次函数,
∴Sn=n2+1 不是等差数列的前n项和的形式,
∴{an} 不是等差数列.
?
能力提升
题型二
“奇、偶项的和”性质及“比值”性质的应用
例题
2.设等差数列{????????},{????????}的前???? 项和分别为????????,????????,若????????????????=????+????????????+????,则????????????????????????= ( )
?
[解析] S19=19a1+a192=19a10,T19=19b1+b192=19b10 ,
所以a10b10=S1919T1919=S19T19=2139=713 .
?
D
A. ???????? B. ???????????????? C. ???????? D. ????????????
?
能力提升
题型二
“奇、偶项的和”性质及“比值”性质的应用
例题
3.已知等差数列{????????},{????????}的前????项和分别为????????,???????? ,????????????????=????????+?????????????????,则???????????????????????? 等
于( )
?
A. ???????????????? B. ???????????????? C. 1 D. 2
?
[解析] 由等差数列的前n 项和公式以及等差中项的性质得
S11=11a1+a112=11a6,同理可得T11=11b6 ,
因此,S11T11=11a611b6=a6b6=2×6+33×6?1=1517 ,故选A.
?
A
能力提升
题型二
“奇、偶项的和”性质及“比值”性质的应用
例题
4. 在项数为 2n+1 的等差数列中,所有奇数项的和为165,所有偶数项的和为150,则 n 等于( @25@ )
A. 9 B. 10 C. 11 D. 12
?
B
[解析] 设该数列奇数项和与偶数项和分别为S1 , S2 ,
则S1S2=n+1a1+a2n+12na2+a2n2=n+1?2an+1n?2an+1=n+1n ,
∴165150=n+1n , ∴n=10 .
?
能力提升
题型二
“奇、偶项的和”性质及“比值”性质的应用
例题
5.在等差数列{????????}中,????????????=???????????? ,且在这10项中,????奇????偶=????????????????,则公差????= ___.
?
2
[解析] 由&S奇+S偶=120,&S奇S偶=1113,
得&S奇=55,&S偶=65,
所以S偶?S奇=5d=10 ,
所以d=2 .
?
能力提升
题型三
“片段和”性质的应用
例题
6. 已知{????????}为等差数列,若????????+????????+????????=????,????????+????????+????????=???????? ,
则????????????+????????????+????????????= ____.
?
[解析] 解法一(“片段和”性质法):记{an}的前n项和为Sn,
因为{an} 是等差数列,所以S3,S6?S3,S9?S6,? ,S21?S18 成等差数列,
设此数列的公差为d,则5+2d=10,所以d=52 ,
所以a19+a20+a21=S21?S18=5+6d=5+15=20 .
解法二(基本量法):设数列{an}的公差为d ,则
a7+a8+a9=a1+6d+a2+6d+a3+6d=5+18d=10 ,
所以18d=5 ,
故a19+a20+a21=a7+12d+a8+12d+a9+12d=10+36d=20 .
?
解题感悟
能力提升
在等差数列中,解决前???? 项和的问题,有时可以利用公式列出关于
????????和???? 的方程(组),进而求解.
有时也可以利用“片段和”性质,用此性质可简化运算.
?
课堂小结
等差数列的前n项和公式的性质
性质4 数列{an}是等差数列?Sn=An2+Bn (A,B为常数).
?
性质5
性质6
性质7
性质8
性质9
第四章 数列
4.2 等差数列
4.2.2 等差数列的前n项和公式(第2课时)
学习目标
1
2
3
理解等差数列的通项公式与前
?
理解并能应用等差数列前n 项和的性质,培育逻辑推理、数学运算的核心素养;
?
能较熟练应用等差数列前n项和公式求和
复习回顾
2.在上一节中我们学习过了等差数列的哪些性质?
1.等差数列的前n项和公式:
“知三求二”
性质1 若{an}是等差数列,公差为d,则ak,ak+m,ak+2m,…(k,m∈N*)是公差为md的等差数列.
性质2 在等差数列{an}中,若m+n=p+q(m,n,p,q∈N*),则am+an=ap+aq.
性质3 数列{an}, {bn}都是等差数列, 公差分别为d1, d2,则数{pan+qbn}(p,q为常数)是公差为pd1+qd2的等差数列.
那么,结合等差数列的前n项和公式,等差数列还会哪些性质?
新课讲授
问题7 已知数列{an}的前n项和为Sn=pn2+qn+r,其中p,q,r为常数,且p≠0.任取若干组p,q,r,在电子表格中计算a1,a2,a3,a4,a5的值(图已给出p=1,q=2,r=0的情况),观察数列{an}的特点,研究它是一个怎样的数列,并证明你的结论.
图中的电子表格A列中A1,A2,A3分别表示p,q,r的值,B列、C列中分别是相应的Sn和an的值.
多给p,q,r取几组值,看看有什么规律?
新课讲授
证明:
结论:若数列{an}的前n项和是一个不含有常数项的二次函数,则该数列是等差数列.
性质4 数列{an}是等差数列?Sn=An2+Bn (A,B为常数).
?
学以致用
教材P24
[例2] 已知一个等差数列{an}前10项的和是310,前20项的和是1220. 由这些条件能确定这个等差数列的首项和公差吗?
例题再现
思考 对于上节课的这道例题中的等差数列,还有其他解法求Sn吗?
解法1:
变式 已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
3. 在等差数列{an}中,Sn为其前n项的和,若S4=6,S8=20,求S16 .
学以致用
教材P23
利用性质4还可以怎样解?
新知探究
证明:
教材P25
性质5
典例分析
变式 已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
思考 利用性质5还可以怎样解?
解法2:
新知探究
问题1
证明:
性质6
典例分析
变式 已知等差数列{an}的n项和为Sn,且S10=310,S20=1220,求S30.
思考 利用性质6还可以怎样解?
解法3:
学以致用
教材P23
5. 已知一个等差数列的项数为奇数,其中所有奇数项的和为290,所有偶数项的和为261. 求此数列中间一项的值以及项数.
问题2 通过解决本题,等差数列又会有什么性质呢?这个性质和什么有关呢?
如果一个等差数列的项数为偶数,又会怎样呢?
新知探究
问题2 通过解决本题,等差数列又会有什么性质呢?这个性质和什么有关呢?
(1)若一个等差数列的项数为奇数,设其项数为2n+1,则
最中间一项
性质7
新知探究
问题2 通过解决本题,等差数列又会有什么性质呢?这个性质和什么有关呢?
(2)若一个等差数列的项数为偶数,设其项数为2n,则
性质8
新知探究
问题3 如果数列{an}、{bn}是项数相同的等差数列,Sn、Tn分别是它们前n项和,那么S2n-1与T2n-1会有什么关系?
性质9
能力提升
题型一
利用数列的前???? 项和判断等差数列
?
例题
1.已知数列{????????}的前????项和????????=????????+???? .
?
(1)求数列{????????} 的通项公式;
?
(2)判断{????????} 是不是等差数列,并说明理由.
?
[解析] (1)当n=1时,a1=S1=12+1=2 ;
当n≥2时,an=Sn?Sn?1=n2+1?n?12?1=2n?1 ,
又a1=2不满足上式,∴an=&2,n=1,&2n?1,n≥2.
?
(2)解法一:∵a1=2,a2=3,a3=5,a2?a1≠a3?a2 ,
∴{an} 不是等差数列.
解法二:∵ 等差数列的前n项和Sn=na1+nn?12d=d2n2+a1?d2n ,
当d2≠0时,其是不含常数项的二次函数,
∴Sn=n2+1 不是等差数列的前n项和的形式,
∴{an} 不是等差数列.
?
能力提升
题型二
“奇、偶项的和”性质及“比值”性质的应用
例题
2.设等差数列{????????},{????????}的前???? 项和分别为????????,????????,若????????????????=????+????????????+????,则????????????????????????= ( )
?
[解析] S19=19a1+a192=19a10,T19=19b1+b192=19b10 ,
所以a10b10=S1919T1919=S19T19=2139=713 .
?
D
A. ???????? B. ???????????????? C. ???????? D. ????????????
?
能力提升
题型二
“奇、偶项的和”性质及“比值”性质的应用
例题
3.已知等差数列{????????},{????????}的前????项和分别为????????,???????? ,????????????????=????????+?????????????????,则???????????????????????? 等
于( )
?
A. ???????????????? B. ???????????????? C. 1 D. 2
?
[解析] 由等差数列的前n 项和公式以及等差中项的性质得
S11=11a1+a112=11a6,同理可得T11=11b6 ,
因此,S11T11=11a611b6=a6b6=2×6+33×6?1=1517 ,故选A.
?
A
能力提升
题型二
“奇、偶项的和”性质及“比值”性质的应用
例题
4. 在项数为 2n+1 的等差数列中,所有奇数项的和为165,所有偶数项的和为150,则 n 等于( @25@ )
A. 9 B. 10 C. 11 D. 12
?
B
[解析] 设该数列奇数项和与偶数项和分别为
则
?
能力提升
题型二
“奇、偶项的和”性质及“比值”性质的应用
例题
5.在等差数列{????????}中,????????????=???????????? ,且在这10项中,????奇????偶=????????????????,则公差????= ___.
?
2
[解析] 由&S奇+S偶=120,&S奇S偶=1113,
得&S奇=55,&S偶=65,
所以S偶?S奇=5d=10 ,
所以d=2 .
?
能力提升
题型三
“片段和”性质的应用
例题
6. 已知{????????}为等差数列,若????????+????????+????????=????,????????+????????+????????=???????? ,
则????????????+????????????+????????????= ____.
?
[解析] 解法一(“片段和”性质法):记{an}的前n项和为Sn,
因为{an} 是等差数列,所以S3,S6?S3,S9?S6,? ,S21?S18 成等差数列,
设此数列的公差为d,则5+2d=10,所以d=52 ,
所以a19+a20+a21=S21?S18=5+6d=5+15=20 .
解法二(基本量法):设数列{an}的公差为d ,则
a7+a8+a9=a1+6d+a2+6d+a3+6d=5+18d=10 ,
所以18d=5 ,
故a19+a20+a21=a7+12d+a8+12d+a9+12d=10+36d=20 .
?
解题感悟
能力提升
在等差数列中,解决前???? 项和的问题,有时可以利用公式列出关于
????????和???? 的方程(组),进而求解.
有时也可以利用“片段和”性质,用此性质可简化运算.
?
课堂小结
等差数列的前n项和公式的性质
性质4 数列{an}是等差数列?Sn=An2+Bn (A,B为常数).
?
性质5
性质6
性质7
性质8
性质9
