4.2.2 对数的运算性质(第1课时) 课件(共33张PPT)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一)
文档属性
| 名称 | 4.2.2 对数的运算性质(第1课时) 课件(共33张PPT)-高一数学考试满分全攻略同步备课备考系列(苏教版2019必修一) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-31 00:00:00 | ||
图片预览











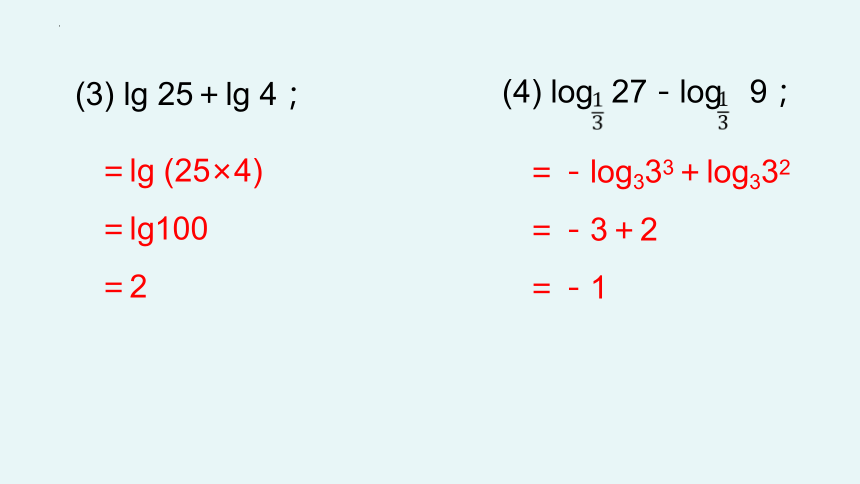
文档简介
(共33张PPT)
苏教版2019高一数学(必修一)第四章 指数与对数
4.2 对 数
4.2.2 对数的运算性质(第1课时)
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
1.理解对数的运算性质.
2.会用对数的运算性质进行一些简单的化简、计算.
3.通过运用对数的运算性质进行化简求值,提升数学抽象素养和数学运算素养.
我们知道,指数幂运算有下列性质:
asat = as+t;
= as-t;
(as)t = ast.
根据对数的定义,有
logaN=b ab = N (a>0,a≠1,N>0).
情景导入
那么,对数运算也有相应的性质吗
设 M=as,N=at,
于是 MN=as+t.
由对数的定义得 logaM=s,logaN=t,
loga(MN) = s+t.
因此,loga(MN) =logaM +logaN.
新知探究
一、对数的运算性质
(1) 性质:
一般地,我们可以得到如下的对数运算性质:
①积的对数:loga(MN) =_________________;
②商的对数:loga=_________________;
③幂的对数:logaMn=____________.
其中a>0,a≠1,M>0,N>0,n∈R.
logaM+logaN
logaM-logaN
nlogaM
(2) 本质:
正用是将积、商、幂的对数进行拆分计算;逆用是将同底数对数的和、差分别合并成积、商计算,数与对数的乘积转化成幂的对数计算.
(3) 应用:
广泛用于对数式的化简求值中,解决对数式的计算问题.
例 4
求下列各式的值:
(1) log2(23×45);
解:=log223+log245
=3+5log24
=3+5×2
=13.
(2) log5125.
解:=log5125
=1og553
=3log55
=3.
课本例题
例 5
已知lg2≈0.3010,lg3≈0.4771,求下列各式的值 (结果保留4位小数):
(1) lg12;
解:=lg(22×3)
=lg22+lg3
=2lg2+lg3
≈2×0.3010+0.4771
=1.0791.
课本例题
(2) lg .
解:=lg(22×3)
=lg33-lg24
=3lg3-4lg2
≈3×0.4771-4×0.3010
=0.2273.
1. 用 lgx,lgy,lgz 示下列各式:
(1) lg(xy2z3);
课本练习
(2) lg.
2. 求下列各式的值:
(1) log3(9×27);
(2) log (45×82);
= log39+log327
=2+3
=5
(3) lg 25+lg 4;
(4) log 27-log 9;
=lg (25×4)
=lg100
=2
=-log333+log332
=-3+2
=-1
3. 已知 lg 2≈0.301 0,lg 3≈0.477 1,求下列各式的值 (结果保留4位小数):
(1) lg 18;
(2) lg 72;
=lg(2×3)
=lg2+2lg3
≈0.3010+2×0.4771
=1.2552
=lg(23×32)
=3lg2+2lg3
≈3×0.3010+2×0.4771
=1.8572
(3) lg ;
(4) lg 15.
= lg(3×2-2)
=lg3-2lg2
≈ 0.4771-2×0.3010
=-0.1249
=lg(10×3÷2)
=1+lg3-lg2
≈1+0.4771-0.3010
=1.1761
4.设 lg 2 = a,lg 3 = b,试用 a,b 表示下列各对数:
(1) lg 108;
(2) lg .
= lg (22×33)
=lg22+lg33
=2lg2+3lg3
=2a+3b
=lg
= lg72 - lg100
= lg (23×32) - lg102
= lg23+lg3-2
= 3lg2 + 2lg3-2
= 3a+2b-2
5. 不用计算器,求下列各式的值:
(1) lg +lg;
(2) log3 45 - log3 5.
= lg(×)
= lg
= lg10
= lg10=
=log3()
=log39
= 2
易错点 忽略底数与真数的范围而致错
B
错因分析
x=5
D
一、选择题
1.计算lg 8+3lg 5的结果为( )
A.-3 B.-1 C.1 D.3
解析 lg 8+3lg 5=3lg 2+3lg 5=3(lg 2+lg 5)=3.
分层练习-基础
A
2.如果lg x=lg a+3lg b-5lg c,那么( )
3.若lg a,lg b是方程3x2-6x+1=0的两个实根,则ab的值等于( )
解析 ∵lg a,lg b是方程3x2-6x+1=0的两个实根,
C
∴ab=100.故选C.
ACD
4.(多选题)下列运算错误的是( )
因为lg(xy)=lg x+lg y,所以2lg(xy)=2lg x+lg y=2lg x·2lg y,故B正确,C不正确;
D中,lg 20+lg 50=lg 1 000=3.故D不正确.
A
log320
=2(lg 2+lg 3)-(lg 10-lg 2)
=3lg 2+2lg 3-1=3a+2b-1.
3a+2b-1
若lg x+lg y=lg(x+y),则lg(xy)=lg(x+y),
∴xy=x+y,
则lg(1-x)+lg(1-y)=lg[(1-x)(1-y)]=lg(1-x-y+xy)=lg 1=0.
解析 若lg(x-y)+lg(x+2y)=lg 2+lg x+lg y,
则lg[(x-y)(x+2y)]=lg(2xy),
∴(x-y)(x+2y)=2xy,
2
0
三、解答题
9.计算下列各式的值:
(2)原式=2log32-(log325-log332)+3log32-5log532
=2log32-5log32+2log33+3log32-9=2-9=-7.
10.设a=lg 2,b=lg 3,试用a,b表示下列各对数:
=2lg 3+lg 2-1=a+2b-1.
1
分层练习-巩固
A
=log28=log223=3.
解析 由2x=3,∴x=log23.
A.3 B.8 C.4 D.log48
13.计算下列各式的值:
(1)log345-log35;
(2)(lg 5)2+2lg 2-(lg 2)2;
(2)原式=(lg 5+lg 2)(lg 5-lg 2)+2lg 2
=lg 10(lg 5-lg 2)+2lg 2
=lg 5-lg 2+2lg 2=lg 5+lg 2=1.
2
分层练习-拓展
课堂小结
苏教版2019高一数学(必修一)第四章 指数与对数
4.2 对 数
4.2.2 对数的运算性质(第1课时)
目录/CONTENTS
新知探究
情景导入
学习目标
课堂小结
分层练习
错因分析
学习目标
1.理解对数的运算性质.
2.会用对数的运算性质进行一些简单的化简、计算.
3.通过运用对数的运算性质进行化简求值,提升数学抽象素养和数学运算素养.
我们知道,指数幂运算有下列性质:
asat = as+t;
= as-t;
(as)t = ast.
根据对数的定义,有
logaN=b ab = N (a>0,a≠1,N>0).
情景导入
那么,对数运算也有相应的性质吗
设 M=as,N=at,
于是 MN=as+t.
由对数的定义得 logaM=s,logaN=t,
loga(MN) = s+t.
因此,loga(MN) =logaM +logaN.
新知探究
一、对数的运算性质
(1) 性质:
一般地,我们可以得到如下的对数运算性质:
①积的对数:loga(MN) =_________________;
②商的对数:loga=_________________;
③幂的对数:logaMn=____________.
其中a>0,a≠1,M>0,N>0,n∈R.
logaM+logaN
logaM-logaN
nlogaM
(2) 本质:
正用是将积、商、幂的对数进行拆分计算;逆用是将同底数对数的和、差分别合并成积、商计算,数与对数的乘积转化成幂的对数计算.
(3) 应用:
广泛用于对数式的化简求值中,解决对数式的计算问题.
例 4
求下列各式的值:
(1) log2(23×45);
解:=log223+log245
=3+5log24
=3+5×2
=13.
(2) log5125.
解:=log5125
=1og553
=3log55
=3.
课本例题
例 5
已知lg2≈0.3010,lg3≈0.4771,求下列各式的值 (结果保留4位小数):
(1) lg12;
解:=lg(22×3)
=lg22+lg3
=2lg2+lg3
≈2×0.3010+0.4771
=1.0791.
课本例题
(2) lg .
解:=lg(22×3)
=lg33-lg24
=3lg3-4lg2
≈3×0.4771-4×0.3010
=0.2273.
1. 用 lgx,lgy,lgz 示下列各式:
(1) lg(xy2z3);
课本练习
(2) lg.
2. 求下列各式的值:
(1) log3(9×27);
(2) log (45×82);
= log39+log327
=2+3
=5
(3) lg 25+lg 4;
(4) log 27-log 9;
=lg (25×4)
=lg100
=2
=-log333+log332
=-3+2
=-1
3. 已知 lg 2≈0.301 0,lg 3≈0.477 1,求下列各式的值 (结果保留4位小数):
(1) lg 18;
(2) lg 72;
=lg(2×3)
=lg2+2lg3
≈0.3010+2×0.4771
=1.2552
=lg(23×32)
=3lg2+2lg3
≈3×0.3010+2×0.4771
=1.8572
(3) lg ;
(4) lg 15.
= lg(3×2-2)
=lg3-2lg2
≈ 0.4771-2×0.3010
=-0.1249
=lg(10×3÷2)
=1+lg3-lg2
≈1+0.4771-0.3010
=1.1761
4.设 lg 2 = a,lg 3 = b,试用 a,b 表示下列各对数:
(1) lg 108;
(2) lg .
= lg (22×33)
=lg22+lg33
=2lg2+3lg3
=2a+3b
=lg
= lg72 - lg100
= lg (23×32) - lg102
= lg23+lg3-2
= 3lg2 + 2lg3-2
= 3a+2b-2
5. 不用计算器,求下列各式的值:
(1) lg +lg;
(2) log3 45 - log3 5.
= lg(×)
= lg
= lg10
= lg10=
=log3()
=log39
= 2
易错点 忽略底数与真数的范围而致错
B
错因分析
x=5
D
一、选择题
1.计算lg 8+3lg 5的结果为( )
A.-3 B.-1 C.1 D.3
解析 lg 8+3lg 5=3lg 2+3lg 5=3(lg 2+lg 5)=3.
分层练习-基础
A
2.如果lg x=lg a+3lg b-5lg c,那么( )
3.若lg a,lg b是方程3x2-6x+1=0的两个实根,则ab的值等于( )
解析 ∵lg a,lg b是方程3x2-6x+1=0的两个实根,
C
∴ab=100.故选C.
ACD
4.(多选题)下列运算错误的是( )
因为lg(xy)=lg x+lg y,所以2lg(xy)=2lg x+lg y=2lg x·2lg y,故B正确,C不正确;
D中,lg 20+lg 50=lg 1 000=3.故D不正确.
A
log320
=2(lg 2+lg 3)-(lg 10-lg 2)
=3lg 2+2lg 3-1=3a+2b-1.
3a+2b-1
若lg x+lg y=lg(x+y),则lg(xy)=lg(x+y),
∴xy=x+y,
则lg(1-x)+lg(1-y)=lg[(1-x)(1-y)]=lg(1-x-y+xy)=lg 1=0.
解析 若lg(x-y)+lg(x+2y)=lg 2+lg x+lg y,
则lg[(x-y)(x+2y)]=lg(2xy),
∴(x-y)(x+2y)=2xy,
2
0
三、解答题
9.计算下列各式的值:
(2)原式=2log32-(log325-log332)+3log32-5log532
=2log32-5log32+2log33+3log32-9=2-9=-7.
10.设a=lg 2,b=lg 3,试用a,b表示下列各对数:
=2lg 3+lg 2-1=a+2b-1.
1
分层练习-巩固
A
=log28=log223=3.
解析 由2x=3,∴x=log23.
A.3 B.8 C.4 D.log48
13.计算下列各式的值:
(1)log345-log35;
(2)(lg 5)2+2lg 2-(lg 2)2;
(2)原式=(lg 5+lg 2)(lg 5-lg 2)+2lg 2
=lg 10(lg 5-lg 2)+2lg 2
=lg 5-lg 2+2lg 2=lg 5+lg 2=1.
2
分层练习-拓展
课堂小结
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
